Example
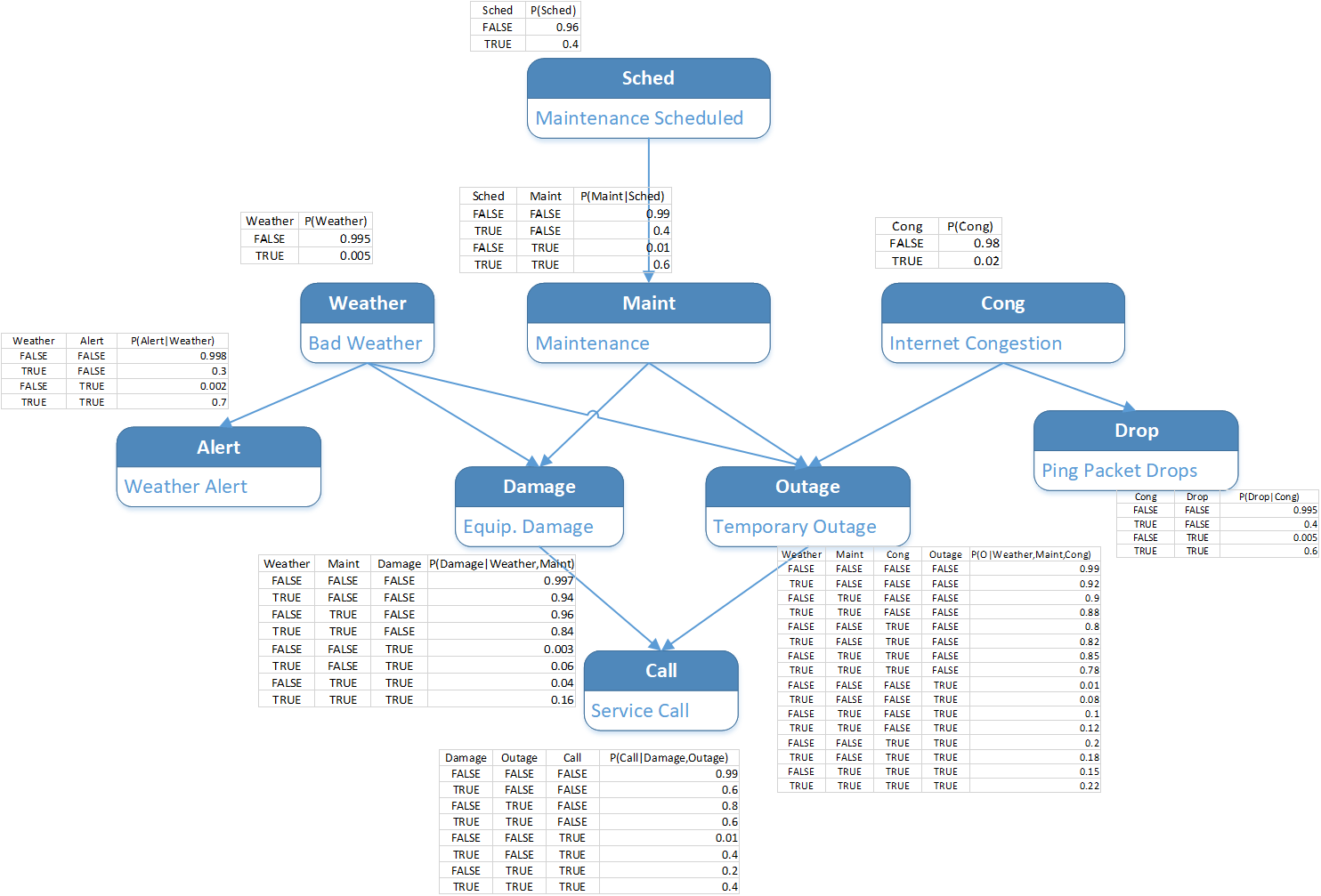This picture describes the model used by an Internet Service Provider to make
certain assertions about current state of the system
- The system has access to the Schedule of Maintenance as well as prior probabilities of scheduled and un-scheduled maintenance
- The system is given probabilities of bad Weather. The system has no direct knowledge of current Weather but has access to Weather Alert. There are statistical probabilities of how often Weather Alert is issued in presence of bad Weather
- The statistical probability of Internet Congestion is known.
- The system is issuing periodic pings to Internet servers and using observed packet loss to improve its awareness of Internet Congestions. The statistical probability between Internet Congestion and Packet Drop is provided.
- The system has the historically-calculated statistical probability of Weather Condition, Maintenance, and Congestion causing Equipment Damage and/or a Temporary Outage
- The system has the historically-calculated statistical probability of Service Calls being received due to Equipment Damage and Outages.
This model can be used to make many assertions, such as:
- When a Service Call is received
(Call=true), by observing the values of Weather Alert(Alert), Packet Drop detector(Drops), and Maintenance Schedule(SCHED), this system can determine the probability of Serious Access Failure(Damage). The ISP could have a policy to send maintenance personnel if this probability is above certain percentage (based on the cost of the crew and outage) - Given observed values of Weather Alert
(Alert), Packet Drop(Drop), and Maintenance Schedule(Sched), this system can determine the probability of receiving Service Calls. The company policy could be to have additional call center crew available whenever the probability of Service Calls is evaluated as being above a certain threshold.
1 VarDb db;
2 db.AddVar("Sched"); // Scheduled maintenance
3 db.AddVar("Maint"); // Maintenance in progress
4 db.AddVar("Weather"); // Bad Rain
5 db.AddVar("Alert"); // Weather alert
6 db.AddVar("Cong"); // Internet congestion
7 db.AddVar("Drop"); // Drop packets
8 db.AddVar("Damage"); // Internet access failure, require roll a track
9 db.AddVar("Outage"); // Temporary Internet outage
10 db.AddVar("Call"); // Service Call received- Scheduled Maintenance Pattern
("Sched")This is an independent variable -- it does not have a parent.
1 VarSet vsSched;
2 vsSched << db["Sched"];
3 std::shared_ptr<Factor> fSched = std::make_shared<Factor>(vsSched, vsSched);
4 fSched->AddInstance(0, 0.96F); // not scheduled 96% of the time
5 fSched->AddInstance(1, 0.04F); // scheduled 4 % of the time(This example illustrates a more "chatty" implementation of factor initialization)
1. An empty _VarSet_ is constructed
2. The _VarSet_ is populated with variables. One in this case
3. A _Factor_ is constructed using this _VarSet_. The _Factor_ constructor
accepts two _VarSets_:
The first _VarSet_ combines all variables in this factor.
The second _VarSet_ consists of variables in the head of the
predicate defining this factor. For single-variable _VarSet_, both
_VarSets_ are same
4. Add the probability of Instance=0.
Instance 0 defines probability of variable `"Sched"=false`.
5. Add the probability of Instance=1.
Instance 1 defines probability of variable `"Sched"=true`.
The following factor initializations utilize more compact two-line factor initializations.
- The Weather Factor describes the probability of bad weather (This and the following following factor initializations utilize more compact factor initialization syntax.)
1 std::shared_ptr<Factor> fWeather(new Factor({db["Weather"]}, { db["Weather"] }));
2 (*fWeather) << 0.995F << fin; // 99.5% of the time the "weather is not bad"1. Factor is created and initialized with "Weather" as the head variable
2. Factor is loaded with the probability of "bad Weather"=false which is 99.5%.
"fin" manipulator automatically completes the factor by loading probability
"bad Weather"=true to 0.5% (complement) to make 100% total
- Load the remaining factors
std::shared_ptr<Factor> fCong(new Factor({ db["Cong"] }, { db["Cong"] }));
(*fCong) << 0.98F << fin; // 98% of time, there is "no congestion"
// Create factor with conditional probability of whether schedule was set for this maintenance
std::shared_ptr<Factor> fSched(new Factor({db["Maint"], db["Sched"]}, {db["Sched"]}));
(*fSched) << 0.99F << 0.4F << fin; // 99% "no unscheduled maintenance", 40% if "scheduled maintenance is not performed"
// Create a factor with conditional probabilities of Alert based on Weather Condition
std::shared_ptr<Factor> fAlert(new Factor({ db["Weather"], db["Alert"] }, { db["Alert"] }));
(*fAlert) << 0.998F << 0.3F << fin; // 99.8% "no bad weather" will not alert, 30% "bad weather" will not cause alert
// Create a factor with conditional probabilities of packet drop based on Internet Congestion
std::shared_ptr<Factor> fDrop(new Factor({ db["Cong"], db["Drop"] }, { db["Drop"] }));
(*fDrop) << 0.995F << 0.4F << fin; // 99.5% "no congestion pings" will not drop, 40% "congestion packet" will not drop
// Probability of damage based on weather condition and maintenance
std::shared_ptr<Factor> fDamage(new Factor({ db["Weather"], db["Maint"], db["Damage"] }, { db["Damage"] }));
(*fDamage) << 0.997F << 0.94F << 0.96F << 0.84F << fin;
// Probability of outage based on weather, maintenance and congestion
std::shared_ptr<Factor> fOutage(new Factor({ db["Weather"], db["Maint"], db["Cong"], db["Outage"] }, { db["Outage"] }));
(*fOutage) << 0.99F << 0.92F << 0.9F << 0.88F << 0.8F << 0.82F << 0.85F << 0.78F << fin;
// Probability of service call based on damage and outage
std::shared_ptr<Factor> fCall(new Factor({ db["Damage"], db["Outage"], db["Call"] }, { db["Call"] }));
(*fCall) << 0.99F << 0.6F << 0.8F << 0.6F << fin;
fs.AddFactor(fMaint);
fs.AddFactor(fWeather);
fs.AddFactor(fCong);
fs.AddFactor(fSched);
fs.AddFactor(fAlert);
fs.AddFactor(fDrop);
fs.AddFactor(fDamage);
fs.AddFactor(fOutage);
fs.AddFactor(fDrop);
fs.AddFactor(fCall);
Create a Clause object containing the data input:
- Maintenance is scheduled
- Packet Drop is not detected
- Weather Alert is detected
- Service Call is received
Clause cSample({
{db["Sched"], true},{ db["Drop"], false },
{ db["Alert"], true }, {db["Call"],true }
});
1 fs.PruneEdges(cSample);
2 fs.ApplyClause(cSample);
3 fs.MaximizeVar(db.GetVarSet());
4 std::shared_ptr<Factor> res1 = fs.Merge();
5 InstanceId instanceMpe = res1->GetExtendedClause(0);
6 VarSet vsMpe = res1->GetExtendedVarSet();
7 Clause clMpe(vsMpe, instanceMpe); 1. Optimize _VarSet_ by removing graph edges that are made irrelevant by the sample
2. Apply the sample
3. Find the most probable clause
4. Merge all the data in _Factorset_ to obtain probability value of most probable clause
5,6,7. Construct the _Clause_ for the MPE by fetching the _VarSet_ and the _InstanceId_ of the solved MPE sample
MPE is a special case of MAP where the subset of variables includes all variables of the model. The found "MAP most probable combination" will not always be the same as the subset of the MPE combination
1 Clause cSample({
2 { db["Sched"], true },{ db["Drop"], false },
3 { db["Alert"], true },{ db["Call"],true }
4 });
5
6 VarSet vsMap({ db["Damage"], db["Outage"] });
7 // all other variables can be eliminated
8 VarSet vsEliminate = fs.GetVarSet()->Substract(vsMap);
9 // find if any variables that can be pruned
10 VarSet vsPrune = vsMap.Disjuction(cSample.GetVarSet());
11 fs.PruneVars(vsPrune);
12 fs.PruneEdges(cSample.GetVarSet());
13 fs.ApplyClause(cSample);
14 fs.EliminateVar(vsEliminate);
15 fs.MaximizeVar(vsMap);
16 std::shared_ptr<Factor> res1 = fs.Merge();
17 VarSet vsMapRes = res1->GetExtendedVarSet();
18 InstanceId instanceMap = res1->GetExtendedClause(0);
19 Clause clMap(vsMapRes, instanceMap);
1-4. Create a sample _Clause_
6. Construct the subset of variables for whom the query will be solved -- MAP variables
8. All the other variables will be eliminated from the subset
10-11. This prunes all of the variables that cannot affect the result of the query
12. Removes the edges that are irrelevant due to the sample
13. Apply the sample
14. Eliminate those variables that are not in a MAP
15. Find the most probable MAP combination
16. Obtain a single _Factor_ containing the result
17-19. Construct the result _Clause_ clMap by packaging map variables --
the calculated MAP result. Notice that vsMapRes has
exactly the same content as vsMap, but, as it cannot be guaranteed that
the order of variables will be same, the vsMapRes should be
used when combined with instanceMap.