-
Notifications
You must be signed in to change notification settings - Fork 98
DItutorial
M Jackson, BlueQuartz Software, LLC., 400 Pioneer Blvd. Springboro, OH 45066, [email protected]
Elena Pascal, Department of Materials Science and Engineering, Carnegie Mellon University, 5000 Forbes Avenue, Pittsburgh, PA 15213-3890, [email protected]
Marc De Graef, Department of Materials Science and Engineering, Carnegie Mellon University, 5000 Forbes Avenue, Pittsburgh, PA 15213-3890, [email protected]
This document is an edited MarkDown version of an article published in Integrating Materials and Manufacturing Innovation (2019, DOI 10.1007/s40192-019-00137-4).
Abstract: Dictionary indexing of electron back-scatter patterns was recently proposed as an alternative to the commercially available indexing packages. In this tutorial paper, we describe in detail the various steps that need to be taken to successfully complete an indexing run on an arbitrary data set. We provide three toy data sets for the reader to experiment with: poly-crystalline Nickel with several different acquisition conditions, orthorhombic forsterite, and a single slice from a large serial sectioning experiment on a Ni-base superalloy. The data files and all files produced by the indexing routine are made available as Supplementary Material.
NOTE THAT SOME ITEMS HAVE CHANGED STARTING IN EMsoft VERSION 5.0.3
Check the wiki page for EBSD Dictionary Indexing for details
The identification of features in diffraction patterns and relating them to the crystal lattice that gave rise to the pattern is commonly known as "indexing the pattern." This can be as simple as assigning Miller indices to the individual peaks of an x-ray powder diffraction (XRD) pattern, or as complex as extracting the location, the orientation, and the stress state of the volume giving rise to a set of diffraction peaks in a High Energy Diffraction Microscopy (HEDM) beam line experiment. The energetic beam used to obtain the diffraction patterns can be formed by x-ray photons, electrons, or neutrons, and a large number of diffraction geometries are in use for each type of beam. We refer to a particular diffraction geometry as a modality to emphasize that the signal collected is dictated by geometry of diffraction. In this tutorial paper, we focus on the indexing of Electron Back-Scatter Diffraction (EBSD) patterns obtained in a scanning electron microscope (SEM), but other SEM modalities (electron channelling patterns (ECP) [degraef2017] and transmission Kikuchi patterns (TKD) [degraef2018]) can be indexed in an analogous manner.
EBSD is recognized as a relatively fast and inexpensive texture analysis technique for a number of different applications with distinct challenges from metals and semiconductors to earth science. In the context of 3D serial sectioning experiments, the EBSD modality takes on a special role since it simplifies significantly the segmentation of individual grains as well as the alignment of consecutive slices. When EBSD patterns are acquired and indexed for each slice, the resulting inverse pole figure maps will, in principle, clearly outline each grain and thus all grain boundaries. For high quality EBSD patterns, the conventional Hough-based indexing process achieves the same end result; however, when (experimental) time is of the essence, it is often easier and cheaper to rapidly acquire low quality patterns. Those patterns can still be indexed using the approach described in this paper, even when the Hough-based approach tends to fail due to the low signal-to-noise ratio.
An EBSD pattern, or EBSP, is formed when a high energy electron beam (typically 10-30 keV) enters a crystalline sample at a shallow incidence angle of around 20°, and the back-scattered electrons are intercepted by a planar detector, usually a scintillator converting the electrons to photons, but more recently also a CMOS direct detector [wilkinson2013] or a digital direct electron detector [vespucci2015] (unfortunately these novel detectors are not widely commercially available at the time of writing this tutorial). As the electrons exit the sample, they channel through the crystal lattice, which modulates the angular distribution of the electrons at the detector. Kikuchi bands, with a width proportional to twice the Bragg angle, are rigidly attached to the crystal lattice, so that determination of the band positions and orientations on the detector allows for the computation of the lattice orientation with respect to the sample reference frame.
This process involves the use of the Hough transform to identify or extract individual Kikuchi bands from the pattern. If the detector-sample geometry has been calibrated accurately, then the band positions can be translated into plane normals, and a comparison of the angles between plane normals (or zone axes) against a pre-computed list of angles based on the known sample crystallography then results in the indexing of individual bands and, subsequently, the determination of the orientation of the crystal lattice. This process is generally well understood and has been implemented by a number of vendors into commercial EBSD packages, several capable of indexing more than 1,000 patterns per second [schwarzer2010].
While Hough-based indexing (HI) has been extremely successful on a broad spectrum of materials and microstructures, there are several circumstances for which the indexing success rate is very low. Since HI depends on the extraction of Kikuchi bands from the pattern, the contrast between the bands and the background is a crucial factor in the extraction process; a low signal-to-noise ratio makes indexing more difficult and, sometimes, impossible, as we will show later in this tutorial paper. Heavily deformed materials also pose problems due to the more diffuse nature of the Kikuchi bands, and the local deviations from the perfect lattice symmetry that is used to compute the interplanar angle look-up table. Low symmetry crystal structures and, in particular, multi-phase mixtures of low symmetry structures, can also pose indexing challenges due to the presence of pseudo-symmetry and potentially very similar phases.
In terms of accuracy of orientation determination, the HI approach is ultimately limited by the precision with which the bands can be localized and identified. The localization confidence is determined by the resolution chosen for the Hough space, which can be improved at the cost of rapidly increasing computation time. The manner in which peak assignment in the Hough space is implemented in commercial algorithms is not well documented and, therefore, the process is not widely understood by the scientific community. It is known however, that, without a sufficient number of peaks in the Hough transform, the algorithm will fail to determine the orientation with a high confidence level. Additionally, the Hough transform assumes Kikuchi bands to be straight lines, when in reality they have thickness and curvature; this is yet another source of systematic error.
Dictionary indexing (DI) provides a powerful alternative to the HI approach because it does not involve feature extraction from the EBSP; the entire pattern is simulated using a physics-based forward model, and matched against the complete experimental pattern. This means that background can be accounted for and low signal to noise images are less of a problem; black box indexing results are avoided since the entire DI implementation is open sourced. The accuracy of orientation determination is theoretically limited by the orientation space sampling grid of the simulated patterns. However, Ram et al. [ram2017] showed that, in practice, the DI approach accuracy is limited only by the precision in determining the detector geometry, which in turn could be improved by refinement to overcome the HI approach inaccuracy.
In section 2, we provide a brief conceptual description of how dictionary indexing works, starting from a forward model for EBSP formation and ending with a discussion of useful pattern similarity metrics. This process has been implemented as part of the EMsoft open-source software package, and in section 2.2 we describe how the user can obtain and install the package; having access to a recent working version of this package is crucial for the remainder of this paper. The reader should ensure that the version of the EMsoft package used is at least 4.2.
Section 3 describes the experimental data collection (3.1) and the various experimental data formats supported by EMsoft (3.2). In the Supplementary Material, we provide three example data sets along with all the scripts and meta-data needed for the reader to perform the indexing computations; the data sets are described briefly in section 3, and consist of a small fcc-Nickel data set collected under three different detector gain settings (3.3.1), a larger orthorhombic forsterite data set (3.3.2) and a single slice from a 1,000-slice Ni-base superalloy data set (3.3.3).
In section 4, we describe a series of steps the user must take in order to prepare for a dictionary indexing run: definition of the crystal structure (4.1); Monte Carlo simulation of the back-scattered electron yield distribution (4.2); and computation of the EBSD master pattern (4.3).
Section 5 describes in considerable detail how the dictionary indexing process can be carried out. We begin with a description of the detector geometry refinement process (5.1), followed by the creation of the DI input file (5.3) and a description of the various output data sets that are generated along the way (5.4). In some cases, an orientation refinement step will be needed, which is described in detail in section 6. We encourage the interested reader to carry out the long series of steps described in this paper to gain a clear understanding of how our open source implementation of the dictionary indexing process works, and we welcome feedback on all aspects of this process.
Dictionary indexing requires the creation of a pattern dictionary, either prior to the indexing run, or on-the-fly. EBSD patterns are simulated using a sequence of programs described in detail in section 4. In this section, we define the pattern similarity metric used for our DI implementation; we also provide the reader with details on how to obtain the executables and the (open) source code.
Consider an experimental data set consisting of
sampling points in the
form of EBSD patterns (ROI stands for Region of Interest). Each
individual pattern has dimensions
pixels before
binning. The intensity in each pixel (i,j) of experimental pattern
(m,n) (
and
) is represented by
and
is typically in the range
, where d is the dynamic
range (bit range) of the detector system; in practice, d=8 and d=12
or 16 are commonly available values. For convenience, we will label
the experimental patterns with a single index
as
. The dictionary patterns are generated using the forward model described in
section 4, and are represented by the intensities
, where the index p corresponds to different crystal orientations:
, with
the number of patterns in the dictionary.
Each pattern can be represented by a unit column vector by converting
the indices (i,j) into a single index ; converting the
intensities to floating point numbers, and dividing them by the norm of
the vector, we obtain normalized pattern vectors
and
, with components
and
. Each unit vector has
components and represents a normalized EBSP. The simplest similarity
metric between pairs of unit vectors is the dot product, which produces
a number in the range [-1,1], equivalent to the cosine of the angle
between the two vectors,
; this is valid in a space of
arbitrary dimension, so that two N-dimensional unit vectors are
similar when the angle
is small. In the DI approach, this very
basic and simple principle is used to compare each experimental pattern,
, against all dictionary patterns,
, by computing a vector
containing
all possible dot products
:
and then ranking the values from large to small. The top dot product
value for a given q is considered to be the best matching dictionary
pattern for the corresponding experimental pattern ;
the next M nearest matches and the corresponding orientations can also
be stored for further statistical analysis [ram2017]. Since each
dictionary pattern
(
)
corresponds to a single orientation, finding the top dot product,
, corresponds to finding the orientation that best matches the experimental pattern
, thereby indexing this experimental pattern.
While more involved similarity metrics could be employed, the inner dot product was shown to be a good proxy for the misorientation between the experimental pattern and simulated patterns as long as a fine enough orientation space is sampled [singh2016]. So far, this method has proven to be robust against noise [wright2015], very similar patterns [burch2017] and pseudo-symmetry [degraef2018].
While the dot product can be implemented efficiently on a CPU, the
computation of dot products between unit vectors of
length
becomes numerically challenging, even in a
multi-core implementation. A Graphical Processing Unit (GPU) has a
significantly larger number of cores than a typical workstation, and
those cores are well suited for dot product computations. Hence, the
EMsoft implementation of dictionary indexing is a hybrid
implementation, using the OpenMP framework to compute dictionary
patterns in parallel on multiple CPU cores, and the OpenCL framework to
compute dot products on the GPU; the current implementation employs only
a single GPU, but the algorithm can be expanded to address multiple
GPUs. The largest data sets indexed thus far in our group at Carnegie
Mellon University are: (1)
patterns of
size
pixels (i.e., pattern vectors of
length 19,200) for a shot-peened aluminum alloy [degraef2018l]; the
dictionary consisted of
patterns, resulting in the
computation of nearly 1.15 trillion dot products; (2) a 3-D serial
sectioning data set of a Ni-based superalloy consisting of
patterns of size 113x113 pixels each
(i.e., pattern vectors of length 12,769) for a total of 117,390,325
patterns, resulting in nearly 40 trillion dot products, and (3) a
1,000-slice serial sectioning data set on a Ni-base superalloy, with
360,000,000 EBSPs (nearly 120 trillion dot products). These numbers
illustrate that the DI approach, in its current implementation, is
computationally intensive and requires multi-processor hardware with at
least one GPU. As we will show later on in this tutorial, this
significant demand on resources and computation time is more than offset
by the quality and accuracy of the resulting orientation maps, in
particular on "difficult samples" for which the traditional HI approach
mostly fails.
Detailed information on how to install and compile the source code repositories, or how to obtain executables from a nightly build site, can be found in the Supplementary Material to this paper, in section SM-1.
Each EMsoft program has the same high level source code structure, and is called (from the command line) in the same way. If EMprogram represents a program name (for instance EMEBSD), then the following command line options can be used:
EMprogram [-h] [-t] [file.nml]
The arguments between square brackets are optional, and are defined as follows:
-
[-h]: (h=help) this argument causes the program to display a list of all available command line arguments and their meaning. The program will quit after printing the help message.
-
[-t]: (t=template) this argument causes the program to create template files for all the name list input files used by the program. For each name-value entry in the template file, a comment line is inserted with a brief explanation of the variable and its units, if appropriate. The user can then copy the template file to a new file with the name list (.nml) extension and edit the file with a regular text editor. The program will quit after generating the template files. Each template file contains the default values for each available parameter.
-
[file.nml]: the main name list file to be used by the program. If no name is present, then the default file name EMprogram.nml will be used. If the provided name list file does not exist, the program will report an error and abort.
Note that there is a series of utility programs that do not follow this convention; these program instead take regular command-line input.
Orientation determination requires a careful definition of all the relevant reference frames. In the case of EBSD, the important reference frames are attached to (1) the crystal lattice; (2) the sample; (3) the microscope stage; and (4) the detector. The ultimate goal of EBSD is to extract the orientations of the grains with respect to the sample reference frame; we refer to an orientation as the rotation needed to bring the sample reference frame into coincidence with the grain reference frame. Since this involves two separate reference frames, the orientation is represented as a passive rotation. Rotation angles are taken to be positive for counterclockwise rotations when looking along the rotation axis towards the origin.
In materials science, the sample reference frame is often described in terms of directions related to the sample processing, e.g., rolling direction (RD), transverse direction (TD) and normal direction (ND). In the earth sciences field, commonly used sample directions include foliation and lineation. The crystal reference frame is a Cartesian reference frame, , connected to the Bravais lattice by means of the following convention (based on the International Tables for Crystallography, Volume A [Itc1996a]):
where is a Bravais lattice vector and
a reciprocal lattice vector. The EMsoft package uses this reference frame to describe crystal quantities in a Cartesian frame; in
particular, grain orientations are described with respect to this Cartesian crystal reference frame.
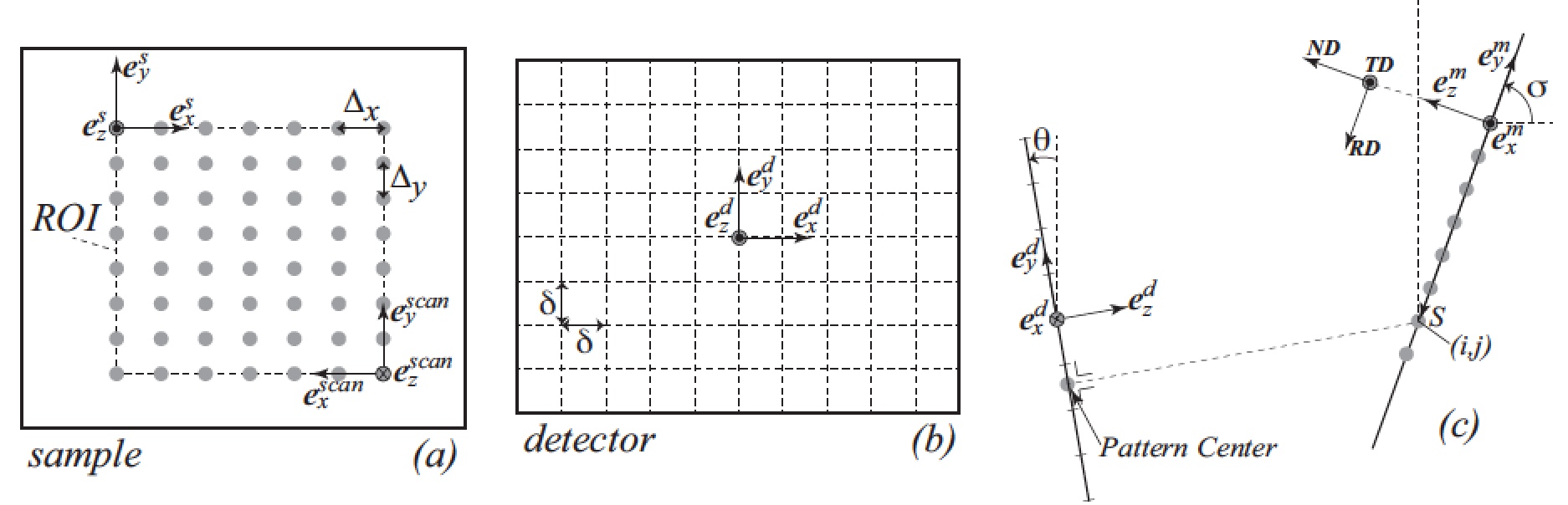 Figure1: Illustration of the reference frames involved in the EMsoft implementation of EBSD. a) shows the sample's right handed reference frame as viewed from the detector, b) the detector's frame as viewed from the sample, with delta the edge size of a pixel and c) the relationship between the two. See the text for further details.
Figure1: Illustration of the reference frames involved in the EMsoft implementation of EBSD. a) shows the sample's right handed reference frame as viewed from the detector, b) the detector's frame as viewed from the sample, with delta the edge size of a pixel and c) the relationship between the two. See the text for further details.
Fig. 1 shows the relevant reference frames in a schematic drawing. Note that the detector reference frame, , has the
axis horizontal and pointing towards the right when looking at the detector from the sample position; the
axis points upward towards the top of the microscope at an angle
with respect to the vertical direction (i.e., the incident beam direction). The microscope stage reference frame,
, has its
axis horizontal and pointing towards the right when looking at the stage from the detector (i.e.,
and
are anti-parallel). The sample is assumed to be mounted so that the transverse direction TD (
) is parallel to the stage
axis. The
axis points up towards the top of the microscope at an angle
from vertical, where
is the sample/stage tilt angle from horizontal. The sample rolling direction RD (
) is anti-parallel to the stage
axis, and
ND.
Looking at the sample from the detector, the EMsoft sample reference frame has its origin on the upper left side of the region of interest (ROI), as shown in Fig. 1(a). The sampling step sizes are along TD, and
along -RD; in the current version of the dictionary indexing algorithm, only square sampling grids of dimension
, with
, are supported. The detector reference frame is shown in Fig. 1(b), looking at the detector from the sample position. In EMsoft, the origin is at the center of the detector, at a
corner point between four pixels; detector pixels are assumed to be square with edge length
(microns). Note that the scan reference frame in commercial packages is typically oriented as indicated in the lower right corner of Fig. 1(a).
In this tutorial paper, we will assume that the sample is mounted and perfectly aligned with the stage reference frame, i.e., the basis vectors are exactly parallel to the
vectors, but rotated clockwise by 90° around the
axis. In principle, sample misalignments, as described in [nolze2007], can be taken into account in the indexing process; they can also be corrected for afterwards, by applying the appropriate rotation to the entire data set.
To ensure a successful dictionary indexing run, this section contains a few tips for the microscope operator that will make the whole indexing process go more smoothly:
-
identify a region of interest (ROI) on your sample for which you want to perform an EBSD scan; set up the proper conditions as you would for any other EBSD scan. Make sure that you set the software to a square sampling grid; hexagonal sampling grids are currently not supported in EMsoft.
-
you will need to store all experimental EBSD patterns on disk; it is not possible to perform DI analysis without those patterns. Depending on your EBSD system, you may be able to store the patterns in an open or proprietary binary format, or in HDF5 format; the formats recognized by EMsoft are described in the following section.
-
before starting the scan, record a single high quality full-size EBSD pattern from a point near the center of the ROI and save this pattern in an image file; this is your reference pattern that will be used to determine accurate detector parameters.
-
without changing any microscope parameters, except for perhaps the pattern binning and the sampling step size, start your data acquisition. Make sure you have recorded the microscope accelerating voltage, sample and detector tilt, detector pixel size, binning factor, sampling step size, and the number of sampling points in the ROI. Most of these are stored in various data files, but you will need them to set up the proper input files for the DI run.
The dictionary indexing approach requires that all experimental EBSPs be stored in a file format that is accessible to EMsoft. Currently, the following file formats are recognized:
-
EMEBSD HDF5 format;
-
EDAX/TSL [up1] and [up2] formats;
-
EDAX/TSL HDF5 format;
-
Bruker HDF5 format;
-
Oxford binary format (uncompressed);
-
MatLab-generated [Binary] format for Oxford patterns.
The EMEBSD format is generated by EMsoft's EMEBSD program when the program is used in dictionary generation mode; this file is needed when static dictionary indexing is carried out, i.e., indexing against a pre-computed dictionary. The EDAX/TSL up1 and up2 formats are simple binary formats in which each intensity is stored as a single byte (up1) or as a two-byte integer (up2); a short 16-byte header precedes the first pattern. Both EDAX/TSL's and Bruker's HDF5 formatted files are the preferred storage modes for EBSPs and they can both be read using various EMsoft programs. At the time of writing of this tutorial, the Oxford Aztec software does not offer the option to store the patterns in a single HDF5 file, but we have been told that this option is in the works; the user can export the patterns from a proprietary binary format to individual image files (.tiff or .bmp format) and employ a Matlab script, provided in the Supplementary Materials section, to convert the individual image files into a single binary data file, which can then be read into EMsoft. The user should note that most operating systems have issues when hundreds of thousands or more image files are stored in a single folder. Alternatively, the uncompressed binary data format can be used for Oxford patterns.
The Ni data file provided as supplementary material (formatted in the EDAX/TSL HDF5 format) contains three EBSD scans of the same region of interest in a polycrystalline sample; the experimental acquisition parameters are listed in Table 1. The data was acquired on an FEI XL30 FEGSEM, and originally indexed using a Hikari camera and the EDAX/TSL OIM acquisition software. The patterns are stored in three different data sets in the HDF5 file, each corresponding to a different camera gain and exposure setting, resulting in a constant exposure level of 90%. The data sets are labeled "Scan 1", "Scan 4", and "Scan 6" in the HDF5 file. The purpose of using this data set as an example is to illustrate the robustness of the dictionary indexing technique against acquisition noise; all three data sets can be indexed with better than 95% success rate using the DI approach.
| Parameter | Value(s) | Parameter | Value(s) |
|---|---|---|---|
| Voltage | 20 kV | Sample tilt | 75.7° |
| Detector Size | 480x480 | Detector Tilt | 10° |
| Binning | 8x8 | Pattern Center | (0.50726,0.73792,0.55849) |
| Scan size | 186x151 | Scan Step Size | 1.5 micron |
| Exposure Level | 90% | Camera Gain | 512,832,896 |
| Camera Exposure [msec] | 0.94,0.23,0.17 | Hough Indexing Rate | 99.1,60.2,19.4 |
Table 1: Acquisition parameters for the Ni data sets accompanying this tutorial paper; for the bottom three entries, three numbers are listed, corresponding to the three data sets in the Ni HDF5 data file (in the order Scan 1, Scan 6, Scan 4).
The forsterite data set was acquired on a Quanta 200 SEM equipped with a Hikari camera using the EDAX/TSL OIM acquisition software. The patterns were acquired in the binary up1 format, along with an .ang file containing several of the acquisition parameters as well as the results from the Hough-based indexing algorithm. The relevant parameters are listed in Table 2. The individual patterns were then aggregated in a single data set using a Matlab script.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Voltage | 20 kV | Sample tilt | 70.0° |
| Detector Size | 488x488 | Detector Tilt | 10° |
| Binning | 8x8 | Pattern Center | (0.4782,0.7982,0.6895) |
| Scan size | 400x401 | Scan Step Size | 1.0 micron |
Table 2: Acquisition parameters for the forsterite/enstatite data set accompanying this tutorial paper.
The third data set made available with this paper is a single slice
(slice number 434) from a larger 1,000-slice data set acquired at
the Air Force Research Laboratory (WPAFB, Dayton, OH) on a Nickel-base
superalloy using a Tescan SEM equipped with the Bruker EBSD package;
acquisition parameters are listed in
Table 3. The serial sectioning data set was
acquired on an automated robot-controlled sectioning implementation
[uchic2012a]. Note that the indexing algorithm can not distinguish
between the
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Voltage | 20 kV | Sample tilt | 70.0° |
| Detector Size | 80x60 | Detector Tilt | -1.3° |
| Binning | 1x1 | Pattern Center | (0.4991,0.4729,0.6698) |
| Scan size | 600x600 | Scan Step Size | 1.0 micron |
Table 3: Acquisition parameters for the Nickel based superalloy data set accompanying this tutorial paper.
Before the DI algorithm can be applied to experimental data, a number of computations must be performed. In this section, we describe a general approach that should be followed in order to correctly set up the necessary input files.
To generate a crystal structure input file (an HDF5 file with default extension .xtal), the user will need the following pieces of information from the literature:
-
Chemical formula or compound/mineral name: this may be useful to generate the filename; e.g., one could use the filename Ni3Al.xtal for the
structure in superalloys, cpx.xtal for the monoclinic clinopyroxene structure, and Nd-garnet.xtal for a neodyium-containing garnet structure.
-
Crystal system: cubic, tetragonal, hexagonal, orthorhombic, rhombohedral, monoclinic or anorthic (triclinic). For the trigonal system, the user is offered both the rhombohedral and hexagonal settings; the hexagonal setting is preferred by most EMsoft programs.
-
Lattice parameters: depending on the crystal system, anywhere from one to six parameters may be needed. In all EMsoft programs, quantities are expressed, whenever possible, in SI based or derived units with their unit prefixes, e.g., lattice parameters are given in nm throughout. Exceptions to this are the electron energies assumed to be in keV and tilt angles given in degrees. All input parameters have their units explicitly stated in the comment lines in the program input files.
-
Space group number: a number between 1 and 230; EMsoft uses the International Tables for Crystallography, Volume A, for all crystallographic conventions. Only standard settings are available for the space groups, but some space groups may have two origin settings.
-
Atom coordinates: for each atom in the asymmetric unit, a triplet of fractional coordinates is needed; optionally, coordinates can be entered as Wyckoff positions.
-
Site occupation parameters: in the range [0..1], these parameters describe the occupation of each lattice site. Generally, those numbers are set to 1.0.
-
Debye-Waller factors: for each atom in the asymmetric unit, the isotropic Debye-Waller factor is needed in units of
. If this factor is not known for the user's material, then one can assign a reasonable default value; experience has shown that a value in the range [0.004..0.006] is almost always a reasonable choice..
The structure information is stored in HDF5 format and can be created either from the command line calling the EMmkxtal program, either entering the input lines one by one or creating an input file redirecting that input to the EMmkxtal command via
$ EMmkxtal < myinputfile,
or via the EMsoftWorkbench GUI. With very few exceptions, all EMsoft programs make use of these crystal structure files.
For the examples made available with this tutorial, three crystal structure files need to be created (they are made available as part of the Supplementary Material):
-
fcc Nickel (Ni): this structure file is easily generated with just a few key strokes. Taking data from Pearson's Handbook [pearson1997], and the room temperature Debye-Waller factor from [peng1996]:
-
Crystal System: 1 (cubic)
-
Lattice Parameter: a=0.35236 nm
-
Space Group: 225
-
Atomic number: 28
-
Atom position, site occupation parameter, Debye-Waller factor: 0,0,0,1.0,0.0035 (
)
-
Output file name: Ni.xtal
-
Source: 'Pearson"s Handbook; Peng et al. 1996'
Note that the Source parameter is a string and should be surrounded by single quotes when entered by the user. If a single quote is needed inside the string, it should be preceded by an escaping quote.
-
-
orthorhombic forsterite (Fo): the structure data can be found in [smyth1973] in the non-standard Pbnm space group setting; since EMsoft only uses the standard setting for orthorhombic and monoclinic space groups, the lattice parameters and fractional coordinates need to be permuted
to obtain the standard Pnma setting.
-
Crystal System: 3 (orthorhombic)
-
Lattice Parameters: a=1.0207 nm, b=0.5980 nm, c=0.4756 nm
-
Space Group: 62
-
Atom position, site occupation parameter, Debye-Waller factor: see Table 4; the table also contains the Wyckoff positions since the EMmkxtal program can be called with the [-w] option.
-
Output file name: Fo.xtal
-
Source: 'Smyth & Hazen, Amer. Mineral. (1973) 58:588-593'
-
| Atom | Z | (x,y,z) | f | B ( |
Wyckoff |
|---|---|---|---|---|---|
| Mg | 12 | (0.0000,0.0000,0.0000) | 1.0 | 0.0026 | 4a |
| Mg | 12 | (0.2774,0.2500,0.9915) | 1.0 | 0.0022 | 4c |
| Si | 14 | (0.0940,0.2500,0.4262) | 1.0 | 0.0008 | 4c |
| O | 8 | (0.0913,0.2500,0.7657) | 1.0 | 0.0027 | 4c |
| O | 8 | (0.4474,0.2500,0.2215) | 1.0 | 0.0024 | 4c |
| O | 8 | (0.1628,0.0331,0.2777) | 1.0 | 0.0027 | 8d |
Table 4: Atom types, positions, site occupations f, and Debye-Waller
factors B along with the Wyckoff symbols for the
forsterite structure in the Pnma setting
[smyth1973].
-
orthorhombic enstatite (En): structure information can be found in [ghose1986] in the Pbca space group setting; there is a small amount of enstatite (
) present in the sample used for this tutorial.
-
Crystal System: 3 (orthorhombic)
-
Lattice Parameters: a=1.8235 nm, b=0.8818 nm, c=0.5179 nm
-
Space Group: 61
-
Atom positions, site occupation parameter, Debye-Waller factor and Wyckoff positions: see Table 5. Note that the Debye-Waller factors are taken to be the average of the diagonal elements of the vibration ellipsoid reported in [ghose1986].
-
Output file name: En.xtal
-
Source: 'Ghose et al., Z. Kristall. (1986) 176:159-175'
-
| Atom | Z | (x,y,z) | f | B ( |
Wyckoff |
|---|---|---|---|---|---|
| Mg | 12 | (0.3758,0.6539,0.8658) | 1.0 | 0.00478 | 8c |
| Mg | 12 | (0.3768,0.4869,0.3588) | 1.0 | 0.00669 | 8c |
| Si | 14 | (0.2717,0.3417,0.0503) | 1.0 | 0.00340 | 8c |
| Si | 14 | (0.4736,0.3373,0.7983) | 1.0 | 0.00335 | 8c |
| O | 8 | (0.1835,0.3401,0.0347) | 1.0 | 0.00472 | 8c |
| O | 8 | (0.5623,0.3403,0.8002) | 1.0 | 0.00479 | 8c |
| O | 8 | (0.3109,0.5025,0.0432) | 1.0 | 0.00578 | 8c |
| O | 8 | (0.4328,0.4829,0.6891) | 1.0 | 0.00580 | 8c |
| O | 8 | (0.3032,0.2226,0.8320) | 1.0 | 0.00575 | 8c |
| O | 8 | (0.4476,0.1951,0.6036) | 1.0 | 0.00544 | 8c |
Table 5: Atom types, positions, site occupations f, and Debye-Waller
factors B along with the Wyckoff symbols for the
enstatite structure [ghose1986].
The forward models used in EMsoft for the simulation of EBSD, ECP, and TKD patterns require knowledge of the energy, depth, and directional distributions of back scattered electrons (BSEs) for a given incident electron energy and sample type and orientation.
The problem of predicting these distributions correctly is a notoriously difficult one [eades2008]. Here we use a Monte Carlo model based on David Joy's implementation of Bethe's Continuous Slowing Down Approximation (CSDA) [joy1995]. This approach simplifies the channels of discrete inelastic scattering by a continuous sum of their effect. The benefit is that the computation can be faster while the downside is that for very small energy losses the prediction is inaccurate.
Recently, Winkelmann et al [winkelmann2019] argued that this approximation leads to incorrect overall energy distributions. They supported this claim by comparing the energy averages of backscattered electrons in different positions on the detector, calculated by Ram et al [ram2018] from CSDA Monte Carlo, with ad-hoc normal energy distributions. They concluded that, since the similarity metric used by them (cross correlation) gives slightly poorer matches when compared to a normal energy distribution centered at the values Ram predicted then the CSDA model must be flawed. This argument is surprising for a number of reasons. First, the real overall backscattered electron distribution is very far from normal and deriving meaning from comparing statistical metrics from different distributions is challenging if not dubious [matejka2017]. Second, the 0.5 keV full width half maximum chosen for the normal distribution does not seem to match experimental evidence of diffraction patterns formed by electrons that lost more than 5 keV energy [deal2005]. Third, as mentioned above, the real overall backscattered energy distribution matches fairly well with Monte Carlo CSDA predictions [deal2008]. The challenge is to improve predictions for low loss electrons and this is a work in progress. The Monte Carlo program is available in two forms, one using the graphical processing unit (using OpenCL), the other operating in multi-threaded mode (using OpenMP).
The energy, depth, and directional distributions of BSEs are computed as histograms. The user has the freedom to decide the smoothness of the energy and depth distributions by trading the number of histogram bins and precision per bin for computation time. The distributions are dependent on material, the geometry of the set up and the incident energy. For energy, the maximum binned energy is the incident energy, i.e., master patterns for a number of different incident energies require the same number of MC computations, while the minimum is the smallest energy to be considered for backscattering; a smaller value than 5 keV is not recommended since the probability that these electrons will contribute substantially to the diffraction pattern is vanishingly small, the MC computation becomes slower since there are more scattering events to track, and the CSDA predictions for low energy electrons are quickly loosing accuracy.
For the examples in this paper, the name list files are identical in all parameters except for the crystal structure file name and the output file name; the sample tilt and microscope accelerating voltage are set to 70° and 20 keV, respectively. The name list file for the EMMCOpenCL program, obtained by calling the program with the [-t] option, has the following relevant entries (other entries should be left at their default values):
&MCCLdata
mode = 'full', ! 'bse1' for ECP; 'full' for EBSD/TKD
xtalname = 'Ni.xtal', ! or 'Fo.xtal' for the forsterite example
sig = 75.7, ! sample tilt angle or 70.0 for Fo/En
numsx = 501, ! # pixels along x-direction [odd number!]
platid = 2, ! GPU platform ID selector (from EMOpenCLinfo)
devid = 1, ! GPU device ID selector
totnum_el = 2000000000, ! total number of incident electrons (< 2^(31)-1)
multiplier = 1, ! use if more than 2^(31)-1 electrons needed
EkeV = 20.D0, ! incident beam energy [keV]
Ehistmin = 10.D0, ! minimum energy to consider [keV]
Ebinsize = 1.0D0, ! energy bin size [keV]
depthmax = 100.D0, ! maximum depth [nm]
depthstep = 1.0D0, ! depth step size [nm]
dataname = 'datapathname/Ni-master-20kV.h5' ! or 'Fo-master-20kV.h5'
! or 'En-master-20kV.h5'
Note the presence of the [datapathname] prefix for the output file name [dataname]; this is the standard EMsoft approach for locating files with respect to a root folder set with the [EMdatapathname] variable in the configuration file (see section SM-1.7 for details). Once the template file is populated with the user's input parameter and its termination is changed from .template to .nml (e.g. on UNIX-like system
$ mv EMMCOpenCL.template myEMMCOpenCL.nml
or using rename on Windows), the EMMCOpenCL program can be called and pointed to the .nml input file:
$ EMMCOpenCL path_to_nml_file/myEMMCOpenCL.nml
If the .nml file is not explicitly provided then the program will look for an input file with the default name EMMCOpenCL.nml file in the current directory.
Execution of the program with either one of these input files will generate an HDF5 file that contains the spatial, energy, and depth histograms used by the next program, EMEBSDmaster. Example output for the Ni structure is shown as a stereographic projection for three different energy bins in Fig. 2; more information can be found in [callahan2013].
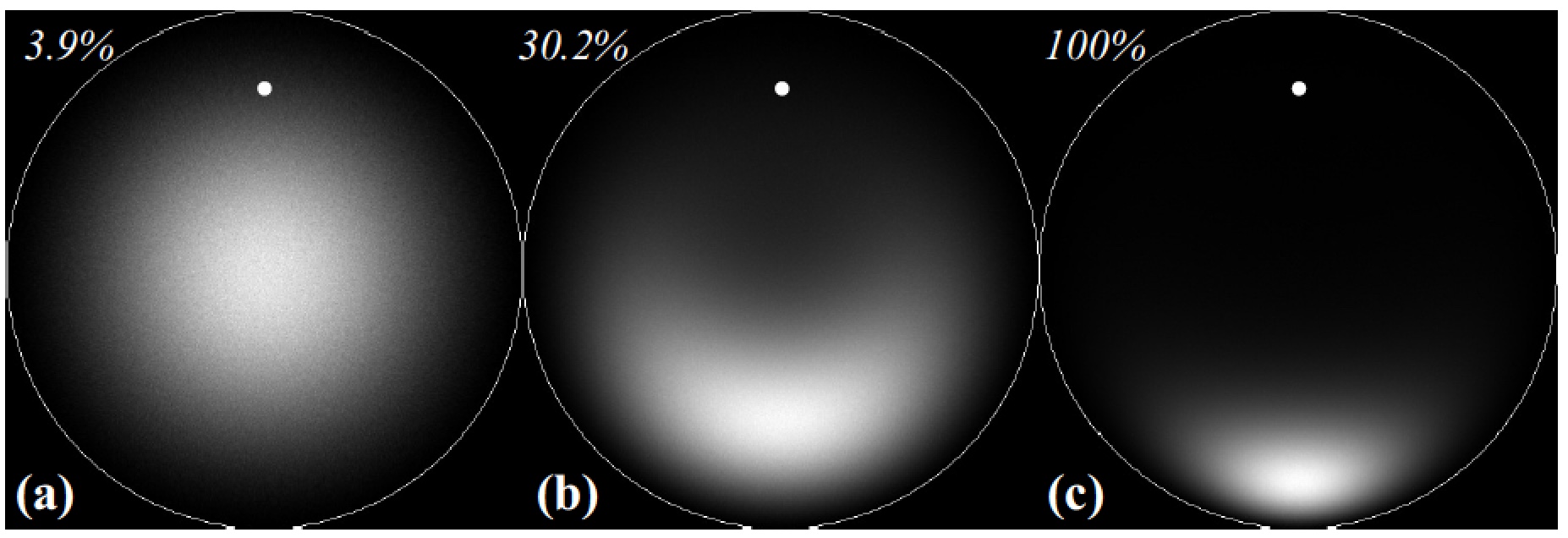
Figure 2: Stereographic projections for Ni for energy bins (a)
The master pattern simulation is typically the most time consuming part of an EBSD pattern simulation sequence, but this has to be carried out only once for a given crystal structure, microscope voltage and sample tilt angle; the master file can be reused often, regardless of the detector parameters.
To set up the simulation parameters, add the [-t] option to the EMEBSDmaster command. This will generate two new files in your folder: EMEBSDmaster.template and BetheParameters.template. The Bethe parameters are used to control the cut-offs for strong beams, weak beams, and beams that can be ignored safely in the dynamical scattering simulations. The default values (see [wang2016] for an extensive description) are appropriate for low to middle range atomic numbers but may need to be increased slightly (10-20%) for heavier elements (e.g., Ag, Au, etc.). For a regular EBSD master pattern computation, simply leave the parameters at their default values and rename the file to BetheParameters.nml. The relevant Bethe parameter file contents for EBSD simulations are:
&Bethelist
! strong beam cutoff
c1 = 4.0,
! weak beam cutoff
c2 = 8.0,
! complete cutoff
c3 = 50.0,
/
Rename the second template file to EMEBSDmaster.nml and edit the relevant parameter values (all other parameters can be left at their default values):
&EBSDmastervars
! smallest d-spacing to take into account [nm]
dmin = 0.05, ! reasonable compromise between speed & accuracy
! # pixels along x-direction of the square master pattern (2*npx+1)^2
npx = 500, ! this value produces good master patterns
! name of the energy statistics file produced by EMMCOpenCL program;
! this file will also contain the output data of the master program
energyfile = 'datapathname/Ni-master-20kV.h5', ! or Fo-master-20kV.h5
! or En-master-20kV.h5
! number of OpenMP threads
nthreads = 1, ! # of threads to be used for computation
/
The [dmin] parameter defines the smallest
The number of pixels parameter [npx] sets the size of the master pattern; the computation time scales with the square of this parameter. A value of 500, which effectively produces a master pattern of size 1,001x1,001, has been found to produce reasonably accurate EBSD patterns for pattern sizes in the range 640x480 and smaller. If larger detectors are to be considered, then the master pattern size parameter may need to be increased to 750 or 1000, with a corresponding increase in computation time.
The nthreads parameter should be set to the number of
cores available on your system. Experience shows that the execution time
of this program scales well with the number of threads used up to the
number
Execution of the EMEBSDmaster program with these input
files (for Ni, forsterite, and enstatite) will store the master patterns
as both square Lambert projections [rosca2010] and stereographic
projections in a new group in the original HDF5 file generated by the
[EMMCOpenCL] program. The Northern hemisphere stereographic
projections for energy bin
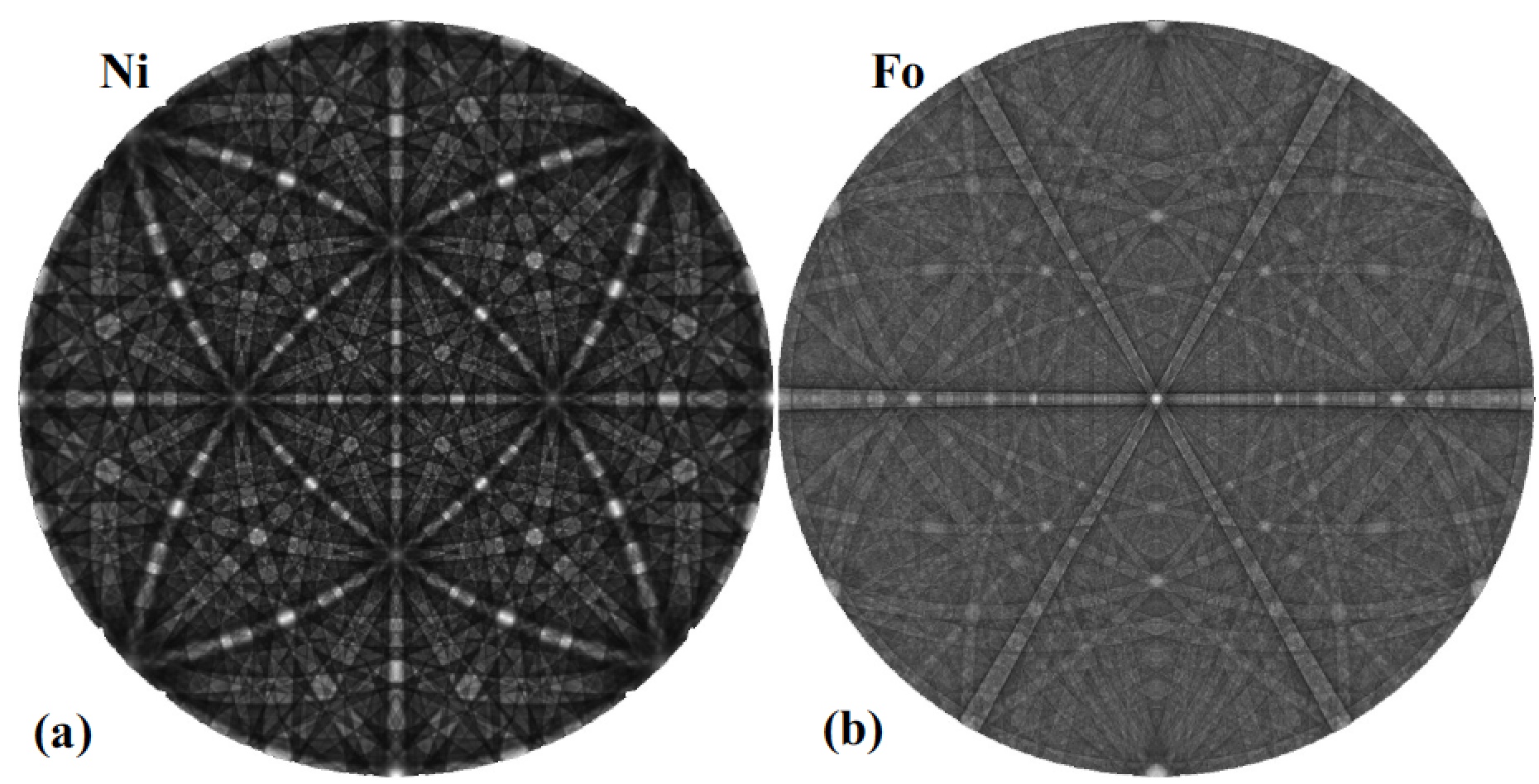
Figure 3: EBSD master patterns for Ni (a) and forsterite (b) for energy bin 18 keV.
Note that the Kikuchi bands are strongly defined in the fcc Ni case, but
are much weaker in the forsterite case. Looking at the most intense
bands, the forsterite master pattern also shows a near hexagonal
symmetry, despite the orthorhombic unit cell. This is a consequence of
the fact that the oxygen lattice is hexagonal close packed, and the
cations occupy the interstitial sites in an orthorhombic arrangement.
Both Mg and Si are light atoms, and we can obtain a simple estimate of
how much each atom species contributes to the master pattern by
multiplying the number of atoms per formula unit by the square of the
atomic number for each species (recall that the Rutherford scattering
cross section is proportional to ). For forsterite, Mg$_2$SiO$_4$,
we obtain the following numbers:
Hence, the anion sub-lattice contributes an estimated
34.6% of the total Rutherford scattering, with Mg and Si contributing
38.9% and 26.5%, respectively. Thus, the hexagonal anion lattice
contributes significantly to the master pattern, which explains the
near-hexagonal appearance when looking along the orthorhombic
It should be noted that the steps carried out thus far (generate crystal structure and perform Monte Carlo and master pattern simulations) can also be carried out from within a graphical user interface (GUI) currently under development. The interface is known as the EMsoftWorkbench and is available through the nightly builds for Mac OS X and Windows 10 platforms. Since this interface is still under development, we will not refer to it any further in the paper.
In this section, we describe in detail how both Ni and forsterite/enstatite data sets can be indexed using the EMsoft programs. We will assume that the reader has already computed the master patterns and has downloaded the data files containing the patterns from the Supplementary Materials web site. The forsterite data set is formatted in the EDAX/TSL [up1] format, i.e., each pixel intensity is represented by a single byte. The three Ni data sets are formatted in the EDAX/TSL [HDF5] format. The slice from the serial sectioning data set from a Nickel-base superalloy is available in the Bruker HDF5 format.
Regardless of the vendor software used to acquire the data, the user
should have an initial estimate of the detector geometry (pattern center
and distance from sample to scintillator). This estimate, which can
typically be found as in an
[.ang] or corresponding file, can be used to start the
geometry refinement, but the parameters must first be converted into the
internal units
and
used by
EMsoft. In principle, this conversion requires knowledge
of the detector pixel size,
; unless a subsequent orientation refinement is carried out (see section 6),
the exact value of
turns out to be unimportant. For the
EDAX/TSL conversion we use the following relations:
where the detector dimensions are pixels before
binning. Since
is proportional to
, any
reasonable value for
will result in a usable value for
;
this is due to the fact that the EBSD pattern will not change if the
detector-sample distance and the pixel size are both scaled by the same
amount. It is only in the refinement step that the true detector pixel
size must be used. Thus, if the pixel size is known, then that value
should be used, otherwise a default value of
micron can be
employed. For the Oxford Instruments [.ctf] file, the
conversion is slightly different:
For the Bruker EBSD system, the pattern center coordinates are defined
with respect to the top left corner of the detector as a fraction of the
detector width and height, respectively, for and
;
the <img src="https://latex.codecogs.com/svg.latex?z^{\ast}" parameter is defined as the ratio of the detector-sample distance to the detector height. This results in the following
conversion expressions to the EMsoft pattern center
coordinates:
For the data sets provided with this tutorial, we find the initial detector parameter sets listed in Table 6. Refinement of these detector parameters requires either the selection of a representative experimental pattern from the acquired data set, or a separate (preferably full size) pattern acquired near the center of the region of interest for the same detector set up.
| Data | (x^{*}, y^{*}, z^{*}) |
|
|
|
|---|---|---|---|---|
| Ni | (0.50726, 0.73792, 0.55849) | 59.2 | (3.4848, 114.2016) | 15,767.7 |
| Fo/En | (0.47821, 0.79819, 0.68948) | 59.2 | (-10.6320, 145.5187) | 19,918.9 |
| Ni-Super | (0.4991, 0.4729, 0.6698) | 50.0 | (-0.55, 13.00) | 16075.2 |
Table 6: Initial detector parameters for the data sets provided with this tutorial; the first two data sets use the EDAX/TSL convention and the third one the Bruker convention.
Using the detector parameters from the original acquisition run as a starting point, we can in principle refine those parameters for the selected Ni and forsterite patterns. From the .ang files we extract the estimated orientations (Euler angle triplets) as initial guesses. There are a number of ways to refine the detector parameters:
-
using the vendor software;
-
interactively, using the IDL GUI [efit];
-
manually, using the EMsoftWorkbench;
-
automatically, using the EMDPFit program
For the present tutorial we recommend that the detector parameter values in Table 6 are used. For the latter three approaches, more detailed information will be made available via the wiki help pages on GitHub; the descriptions are too extensive to be discussed in detail in the present paper.
The pattern pre-processing parameters consist of the high-pass filter
parameter,
From the ADP maps one can select a single pattern from a relatively large grain near the center of the map; the pixel coordinates of this point must be determined with respect to the upper-left corner. For the Ni data set, we select the point with coordinates (85,75) in ADP map Fig. SM-1(a) of the Supplementary Material, for forsterite we select the point with coordinates (138,269) in Fig. SM-1(d), and for the Ni-base superalloy the point with coordinates (243,286) in Fig. SM-1(e). These EBSD patterns, shown in Fig. 4, can be used to optimize the pattern pre-processing parameters.

Figure 4: Experimental patterns corresponding to the marked positions in the ADP maps (Fig. SM-1); the Ni-1, Ni-4, and Ni-6 patterns are 60x60 pixels, Forsterite (Fo) 61x61, and Ni-Super 80x60.
Both sets of experimental and simulated patterns undergo two pre-processing steps, a high-pass filtering operation, which removes most of the background intensity variations (noise), and adaptive histogram equalization, which levels the intensity histogram of each pattern. This makes sure no spurious effects are picked up by the similarity metric. Fig. 5 illustrates the effect of adaptive histogram equalization on the an experimental pattern selected in the previous section from the forsterite data set. The EMEBSDDIpreview program can be used to generate a tiff output file containing an array of pre-processed patterns for a range of filter settings. The program parameters for the pre-processing of pattern (patx, paty) = (243,286) of the Ni superalloy data set are as follows:

Figure 5: Array of pre-processed patterns for the Ni-base superalloy reference pattern; the high-pass parameter varies from left to right, the number of regions in the adaptive histogram equalization from bottom to top. The outlined image represents a set of parameters that typically results in a high indexing rate for the dictionary indexing approach.
&EBSDDIpreviewdata
numsx = 80, ! number of pattern pixels along x (Nx)
numsy = 60, ! and along y (Ny)
ipf_wd = 600, ! number of patterns along horizontal axis (Nh)
ipf_ht = 600, ! and along vertical axis (Nv)
hipasswmax = 0.5, ! hipass width parameter maximum (starts near zero)
hipasswnsteps = 10,! and number of steps
nregionsmin = 1, ! minimum # regions for adaptive histogram equalization
nregionsmax = 10, ! maximum number
nregionsstepsize = 1, ! step size
! preprocessed pattern tiff file
tifffile = 'DItutorial/NiSuper/NiSuper-matrix.tiff',
! raw original pattern tiff file
patternfile = 'DItutorial/NiSuper/NiSuper-reference.tiff',
exptfile = 'DItutorial/NiSuper/Bruker-NiSuper.h5', ! data file
inputtype = 'BrukerHDF', ! input file type
HDFstrings = 'LEROY_0089_Section_434' 'EBSD' 'Data' 'RawPatterns' , ! HDF path
patx = 243, ! pattern coordinate x to be used for the preview
paty = 286, ! y coordinate
/
The EMEBSDDI program takes many parameters via the usual name list mechanism; the template file is generated in the usual way using the [-t] option. The input parameters are grouped in several sections that we will describe one by one.
&EBSDIndexingdata
!###################################################################
! INDEXING MODE
!###################################################################
!
! 'dynamic' for on the fly indexing or 'static' for
! pre-calculated dictionary
indexingmode = 'dynamic',
! ...
The [indexingmode] can take two values: [dynamic] or [static]; in static mode, the program will use an existing dictionary file created by the [EMEBSD] program (see wiki help page on GitHub for additional information). This mode is only recommended if you have many data sets to index and they all have the same detector parameters (for instance, multiple slices from a serial sectioning FIB experiment). This requires a computer with a lot of memory (many tens of Gb of RAM, and lots of disk space). In the dynamic indexing mode, the dictionary patterns are generated on-the-fly during the indexing process; this would be the typical mode for a single data set similar to the ones provided with this tutorial. In that case, having a computer with a large number of cores will speed up the process.
!###################################################################
! DICTIONARY PARAMETERS: COMMON TO 'STATIC' AND 'DYNAMIC'
!###################################################################
! do you want Email or Slack notification when the run has completed?
Notify = 'Off',
ipf_wd = 100, ! width of data set in pattern input file or Nh
ipf_ht = 100, ! height of data set in pattern input file or Nv
! define the region of interest as ROI = x0 y0 w h;
! Leave all at 0 for full field of view.
! Region of interest has the point (x0,y0) as
! its lower left corner and is w x h patterns
ROI = 0 0 0 0,
stepX = 1.0,
stepY = 1.0, ! X and Y sampling step sizes
nnk = 50, ! # top matches to keep
nnav = 20, ! # top matches used for orientation averaging (<nnk)
nosm = 20, ! # top matches used for OSM computation
maskpattern = 'n', ! mask 'y' or 'n'
maskradius = 240, ! mask radius (pixels, AFTER binning)
hipassw = 0.05, ! high pass filter width parameter; 0.05 is reasonable
nregions = 10, ! # regions for adaptive histogram equalization
! ...
The parameters in this block are common to the dynamic and static indexing modes. Since the final output of indexing is usually an inverse pole figure (IPF) map, one must specify the IPF width and height, in pixels, ([ipf_wd, ipf_wd]) for the complete data set; as an example, let us consider a data region of 600x400 pixels. One can then select a sub-region via the [ROI] parameter, which has four integers; if all integers are set to 0, then the complete 600x400 ipf is indexed. If the integers are [60,100,200,200], then a square area of 200x200 pixels is selected with one corner located at the point (60,100). The sampling step size is next and is specified in microns. The next three integers ([nnk, nnav], and [nosm]) define, respectively, how many of the top matches should be kept in the output file (typically about 30 would be useful); how many of the top matches should be used to generate an IPF with orientations averaged over the top [nnav] matches; and how many top matches should be used to generate the orientation similarity map (OSM). Then the user can specify the filename for an optional mask file; this is currently an experimental option in which one can define an arbitrary mask to be applied to the patterns before indexing. For details of the file format, see the wiki help page. If [maskpattern] is set to ['y'], then a circular mask of radius [maskradius] will be applied before indexing; this can be used to exclude the outer portion of the patterns. Finally, the [hipassw] and [nregions] parameters define the pre-processing parameters for the high pass filtering and adaptive histogram equalization steps that all patterns (both experimental and simulated) undergo before indexing; these were discussed in section 5.2.
!###################################################################
! ONLY SPECIFY WHEN INDEXINGMODE IS 'DYNAMIC'
!###################################################################
ncubochoric = 100, ! # cubochoric points to generate orientation list
L = 15000.0, ! distance scintillator - illumination point [microns]
thetac = 10.0, ! camera tilt [degrees]
delta = 50.0, ! CCD pixel size on scintillator [microns]
numsx = 640, ! # CCD pixels along x
numsy = 480, ! and y
xpc = 0.0, ! pattern center x [pixels]
ypc = 0.0, ! pattern center y
omega = 0.0, ! angle between normal of sample and detector [RD, degrees]
energymin = 10.0, ! minimum energy to use for interpolation [keV]
energymax = 20.0, ! maximum energy
beamcurrent = 150.0, ! incident beam current [nA] (irrelevant, but not zero)
dwelltime = 100.0, ! beam dwell time [micro s] (irrelevant, but not zero)
binning = 1, ! binning mode (1, 2, 4, or 8)
scalingmode = 'not', ! intensity scaling mode 'not' = no scaling,
! 'lin' = linear, 'gam' = gamma correction
gammavalue = 1.0, ! gamma correction factor
!...
In this block we define the detector parameters and the orientation sampling. The [ncubochoric] parameter defines the angular step size in orientation space; typically a value of 100, corresponding to an angular step size of 1.4°, will produce good results. The detector parameters are L (distance from scintillator to detector in microns), thetac (detector tilt from vertical in degrees), CCD pixel size in microns, the number of detector pixels along x and y directions, the pattern center in units of pixel size, omega (sample misalignment along RD axis in degrees), the energy range to be used in the pattern interpolation, beam current and dwell time (the actual values don't really matter for indexing, as long as they are both non-zero), binning factor, scalingmode (typically you would use gamma scaling), and the gamma value (0.33 is a good value).
!###################################################################
! INPUT FILE PARAMETERS: COMMON TO 'STATIC' AND 'DYNAMIC'
!###################################################################
exptfile = 'undefined', ! data file location [w.r.t. EMdatapathname]
inputtype = 'Binary', ! input file type parameter: Binary, EMEBSD,
! TSLHDF, TSLup1, TSLup2, OxfordHDF,
! OxfordBinary, BrukerHDF
HDFstrings = '' '' '' '' '' '' '' '' '' '', ! data set full path & name
! ...
Next, we have information about the pattern input file. There are several types (described in section 3.2) and the correct type should be entered in the [inputtype] variable. The file name goes in the [exptfile] parameter (along with the appropriate partial path). If the input file is an HDF5 file, then you must define the complete path inside this file. For instance, if the pattern data set is called [EBSDpatterns], and it is located inside a nested group [Scan 1/data/EBSD], as it is for one of the Ni data sets, then you would enter four strings for [HDFstrings]: 'Scan 1', 'data', 'EBSD', and the last one is the data set name 'EBSDpatterns'. Note that these strings are all case sensitive, so make sure you get them right. You can use the [HDFView] program from the HDF Group to figure out what the correct strings are. Leave the other strings (there are 10 in total) empty.
!###################################################################
! OTHER FILE PARAMETERS: COMMON TO 'STATIC' AND 'DYNAMIC'
!###################################################################
tmpfile = 'EMEBSDDict_tmp.data', ! temporary data storage file name;
! stored in HOME/.config/EMsoft/tmp
keeptmpfile = 'n', ! keep or delete tmp file ?
datafile = 'undefined', ! output file; path relative to EMdatapathname
ctffile = 'undefined', ! ctf output file; path relative to EMdatapathname
! angfile = 'undefined', ! ang output file; path relative to EMdatapathname
eulerfile = 'undefined' ! euler angle input file
! ...
This block defines where all the results and temporary files will be kept. The indexing program uses a temporary file with the pre-processed patterns in the standard tmp folder (usually in the [.config/EMsoft/tmp] folder in your user home directory). You need to define the name of this temporary file in the [tmpfile] variable (no path necessary); it is important to pick a unique name if you are running multiple simultaneous indexing runs. You can keep the file if you want by setting [keeptmpfile] to 'y'. The indexing output is stored in two or three files: [datafile] is an HDF5 output file that has all the program output in it, whereas [ctffile] is the standard Oxford .ctf output file that can be read by most EBSD analysis programs. For the EDAX/TSL [.ang] output file, fill in the desired file name in the [angfile] variable; both [.ctf] and [.ang] files can be created in the same program run. If you set the [eulerfile] parameter to anything other than 'undefined', then the program will use the orientations in that file instead of the cubochoric sampling of orientations controlled by the [ncubochoric] parameter. This can be useful if you know that all the orientations are clustered around some orientation; you can then use the [EMsampleRFZ] program to generate a uniform sampling around that orientation instead of sampling the complete Rodrigues fundamental zone.
!###################################################################
! ONLY IF INDEXINGMODE IS STATIC
!###################################################################
dictfile = 'undefined', ! filename of dictionary file,
! path relative to EMdatapathname
!
!###################################################################
! ONLY IF INDEXINGMODE IS DYNAMIC
!###################################################################
masterfile = 'undefined', ! master pattern input file;
! path relative to EMdatapathname
! ...
In static indexing mode, this is where you define the file that has the complete dictionary in it. Dictionary files can get very, very large, so be careful if you decide to use static indexing. It can be useful for serial sectioning data sets, where you use the same dictionary for all consecutive slices. In our experience, it is usually best to use the dynamic indexing mode when working with single region-of-interest data sets. In dynamic mode, you need to define the master pattern file from which all the dictionary patterns are computed.
!###################################################################
! SYSTEM PARAMETERS: COMMON TO 'STATIC' AND 'DYNAMIC'
!###################################################################
numdictsingle = 1024, ! # dictionary patterns in column for dot product
! on GPU (multiples of 16 perform better)
numexptsingle = 1024, ! # experimental patterns in column for dot product
! on GPU (multiples of 16 perform better)
nthreads = 1, ! # threads for parallel execution
platid = 1, ! platform ID for OpenCL portion of program
! if you are running EMEBSDDI, EMECPDI, EMTKDDI, then define the
! device you wish to use
devid = 1, ! device ID
multidevid = 0 0 0 0 0 0 0 0, ! leave unchanged
usenumd = 0, ! # GPU devices do you want to use?
/
This final block controls the computational resources. In its present form, dictionary indexing requires a GPU (graphical processing unit); use the EMOpenCLinfo program to figure out the platform and device IDs for the GPU that you intend to use for indexing. In the current implementation, only one single GPU can be used, but the name list file already allows for multiple devices. If the GPU you want to use is part of platform 2, and is device number 4, then set [platid] to 2 and [devid] to 4; also, put [usenumd] to 1 and the first entry of [multidevid] to the same number as [devid]. The [nthreads] parameter defines how many CPU cores (threads) you want to use for the pattern computations; the GPU takes care of computing the pattern dot products while the threads compute patterns. Finally, the [numdictsingle] and [numexptsingle] parameters define how large the memory chunks are that the program will send to the GPU; for optimal performance, this number should be a multiple of 16. If you set these parameters too large, then the GPU may not have sufficient global memory to perform the computations, and the program will likely abort with an error message. It is suggested that you keep both numbers set to the same value. If your pattern size is 640x480, then the patterns will be organized as 1D vectors of length 307,200 components each, and the GPU will receive two arrays of single precision floating point numbers (4 bytes each) of dimensions 307,200 by [numdictsingle]. You can easily check whether or not your GPU will be able to accommodate this array size.
At this point we are ready to execute the EMEBSDDI indexing program; simply enter the name of the program followed by the name of the input name list file and hit return. The program will provide progress updates and estimates of the time remaining until completion. Generally, it is a good idea to run long indexing processes on UNIX-type platforms in the background using [nohup]:
$ nohup EMEBSDDI EMEBSDDI-Ni.nml > EMEBSDDI-Ni.out 2> EMEBSDDI-Ni.err &
Alternatively, one can install and run the screen facility. Both these packages allow for the user to log out of the account (close the terminal) without interrupting the execution. It is possible to have the program send out an email or Slack message when the run has ended; see the [Package Configuration] wiki help page on the main source code repository for details. For serial sectioning experiments, where many individual slices need to be indexed, one can script the indexing process using Python, MatLab, or any other scripting language; in that case, the script should generate the name list input files, and spawn the shell command to execute the indexing program.
Indexing the tutorial data sets produces six HDF5 output files as well as [.ctf] and [.ang] files that can be downloaded as part of the Supplementary Material. The dot product HDF5 files contain many data items that are described in a bit more detail in the Supplementary Material, section SM-2. The [.ctf] and [.ang] files created by the indexing program can be read by the regular vendor software, so that the standard operations on orientation data sets can also be carried out on the results of the dictionary indexing runs. A utility program is provided to extract five different maps from the dot product HDF5 file. The program EMdpextract takes a dot product HDF5 file as input and generates, in a separate folder, a confidence index (CI) map, an image quality (IQ) map, an average dot product (ADP) map, kernel average misorientation (KAM) map (without an angular threshold) and an orientation similarity (OS) map. For the definitions of these maps we refer the interested reader to reference [degraef2017e]. Fig. 6 shows the ADP, IQ, CI, and OSM maps for the Nickel superalloy data set. Maps for all other data sets as well as inverse pole figure (IPF) maps are available as Supplementary Material.

Figure 6: Maps extracted from the dot product HDF5 file for the Ni superalloy data set using the [EMdpextract] program. The maps are the average dot product map (ADP), the image quality map (IQ), the confidence index map (CI), and the orientation similarity map (OSM).
The DI implementation makes use of a discrete grid of orientations to compute the dictionary patterns. Since the true orientation for a particular EBSD pattern is likely to fall in between multiple grid points, this means that there is always an angular accuracy associated with each indexing run. The average semi-distance between neighboring orientation grid points is a reasonable estimate for the angular accuracy; for a cubochoric sampling parameter of N=100, the average angular step size in degrees can be parameterized as:
The estimated orientation accuracy, , is then half of this value,
or 0.686° for N=100; in other words, the difference between
the true orientation and the measured orientation, when expressed as a
misorientation angle, lies generally between 0° and
. This value can be improved upon by performing a refinement of the
orientations by allowing each orientation to deviate from the discrete
grid points. This can be done by means of a grid that is repeatedly
(hierarchically) refined, or by a numerical minimization.
The EMFitOrientation program takes the following name list as input:
&RefineOrientations
! number of parallel threads to use for refinement run
nthreads = 1,
! name of input dot product HDF5 file
dotproductfile = 'undefined',
! name of ctf output file for refined orientations
ctffile = 'undefined',
! name of temporary file for pre-processed patterns
! (will override the temporary file name defined in the dot product file)
tmpfile = 'undefined',
! modality ('EBSD' or 'ECP')
modality = 'EBSD',
! keep the pre-processed patterns all in memory?
inRAM = .FALSE.,
! how many items from the top matches list need to be refined?
matchdepth = 1,
! refinement method:
! 'SUB' : refinement by hierarchical sub-sampling of cubochoric grid
! 'FIT' : fit by "bound optimization by quadratic approximation" (BOBYQA) in
! homochoric space (generally faster than SUB)
method = 'FIT',
! ===================================
! if method == 'SUB'
! number of hierarchical iterations
niter = 1,
! number of points sampled around given point [(2*nmis+1)^3]
nmis = 1,
! ===================================
! if method == 'FIT'
! max step size to take in homochoric space during the refinement
step = 0.03,
! In FIT mode, this program can also include pseudo-symmetric variants
! in the list of starting orientations to refine. Pseudo-symmetric variant
! Euler triplets or axis-angle pair(s) are stored in the PSvariantfile.
! format: first line 'ax', second line number of axis-angle pairs,
! then one pair per line (unit vector, angle last in degrees)
! or format: first line 'eu', second line number of Euler triplets,
! then one triplet per line (in degrees)
PSvariantfile = 'undefined',
! ===================================
/
The program can operate in a hierarchical refinement [SUB] mode, in which the cubochoric grid is [niter] times step-wise refined by a factor of two, or a minimizing [FIT] mode, in which the highest dot product is sought inside a box of edge length 2 x step in homochoric space. If [matchdepth] is set to 1, then only the best match from the dictionary indexing is refined; if necessary, the next best N matches can be refined by setting [matchdepth] to N+1. Finally, for some structures multiple orientations can produce EBSD patterns that are very similar (pseudo-symmetry); by defining the rotations that connect pseudo-symmetric orientations in the [PSvariantfile], either in axis-angle pair format or as an Euler angle triplet, the program can be made to refine the dot product for all potential pseudo-symmetric orientations. The refinement program adds data sets to the dot product file generated by the dictionary indexing program (EMEBSDDI), and, optionally, generates an [.ang] or [.ctf] file that can be read by the vendor software for further analysis.

Figure 7:
In this tutorial, we have described in detail the process that needs to be carried out to index an EBSD data set using the dictionary indexing approach that is part of the EMsoft open source package. The final indexing results for the data sets made available with this paper are shown in Fig. 7 as [001] inverse pole figure (IPF) maps. Additional maps can be extracted from the dot product HDF5 files, and the standard vendor software can be used to explore the .ang and .ctf output files generated by the indexing and refinement programs.
The Supplementary Material pdf file, all experimental data sets, the crystal structure files, the program input files, and all output generated by the indexing and refinement programs are made available via the KiltHub data repository at Carnegie Mellon University at the following URL: http://doi.org/10.1184/R1/7792505. The ReadMe.txt file in this repository describes all the data sets and files in detail.
The minimum EMsoft version needed to perform all the indexing steps and regenerate the output files is version 4.2, which is available via the following DOI: http://doi.org/10.5281/zenodo.2581285. Finally, all EMsoft-related material and links are made available via the URL http://vbff.materials.cmu.edu/EMsoft.
The authors would like to thank Stuart Wright, Katharina Marquardt, and Michael Uchic for making experimental data sets available and allowing us to make them publicly accessible. We would like to thank Melanie Gainey and the KiltHub team at Carnegie Mellon University for their support in permanently hosting the data files. The authors would like to acknowledge funding from a DoD Vannevar-Bush Faculty Fellowship (# N00014-16-1-2821) as well as the computational facilities of the Materials Characterization Facility at CMU under grant # MCF-677785.
Burch, M.J., Fancher, C.M., Patala, S., De Graef, M., Dickey, E.C.: Mapping 180$^{\circ}$ polar domains using electron backscatter diffraction and dynamical scattering simulations. Ultramicroscopy 173, 47--51 (2017)
Callahan, P., De Graef, M.: Dynamical EBSD patterns Part I: Pattern simulations. Microscopy and MicroAnalysis 19, 1255--1265 (2013)
De Graef, M., Lenthe, W.C., Schäfer, N., Rissom, T., Abou-Ras, D.: Unambiguous determination of local orientations of polycrystalline CuInSe$_2$ thin films via dictionary-based indexing. physica status solidi (RRL)--Rapid Research Letters p. 1900032 (2018)
Deal, A., Eades, A.: Energy-dependence of an EBSD pattern. Microscopy and Microanalysis 11(S02), 524--525 (2005)
Deal, A., Hooghan, T., Eades, A.: Energy-filtered electron backscatter diffraction. Ultramicroscopy 108(2), 116--125 (2008)
Eades, A., Deal, A.: Why is it difficult to simulate EBSD patterns accurately? Microscopy Today 16(3), 50--51 (2008)
Ghose, S., Schomaker, V., McMullan, R.: Enstatite, Mg$_2$Si$_2$O$_6$: A neutron diffraction refinement of the crystal structure and a rigid-body analysis of the thermal vibration. Z. Kristall. 176, 159--176 (1986)
Hahn, T. (ed.): The International Tables for Crystallography Vol A: Space-Group Symmetry., vol. A. Kluwer Academic Publishers, Dordrecht (1996)
Joy, D.: Monte Carlo Modeling for Electron Microscopy and Microanalysis. Oxford University Press, USA (1995)
Marquardt, K., De Graef, M., Singh, S., Marquardt, H., Rosenthal, A., Hiraga, T.: Quantitative electron backscatter diffraction (EBSD) data analyses using the dictionary indexing (DI) approach: overcoming indexing difficulties in gological materials. American Mineralogist 102, 1843--1855 (2017)
Matejka, J., Fitzmaurice, G.: Same stats, different graphs: Generating datasets with varied appearance and identical statistics through simulated annealing. In: Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems, pp. 1290--1294. ACM (2017)
Nolze, G.: Image distortions in SEM and their influences on EBSD measurements. Ultramicroscopy 107, 172--183 (2007)
Pascal, E., Singh, S., Callahan, P., De Graef, M.: Energy-weighted dynamical scattering simulations of back-scattered electron diffraction modalities. Ultramicroscopy 187, 98--106 (2018)
Peng, L.M., Ren, G., Dudarev, S., Whelan, M.: Debye-Waller Factors and Absorptive Scattering Factors of Elemental Crystals. Acta Crystallographica Section A: Foundations of Crystallography 52, 456--470 (1996)
Ram, F., De Graef, M.: Energy dependence of the spatial distribution of inelastically scattered electrons in backscatter electron diffraction. Physical Review B 97(13), 134104 (2018)
Ram, F., Wright, S., Singh, S., De Graef, M.: Error analysis of the crystal orientations obtained by the dictionary approach to EBSD indexing. Ultramicroscopy 181, 17--26 (2017)
Roşca, D.: New uniform grids on the sphere. Astronomy & Astrophysics 520, A63 (2010)
Schwarzer, R.A., Hjelen, J.: Orientation microscopy with fast EBSD. Materials Science and Technology 26(6), 646--649 (2010)
Singh, S., De Graef, M.: Orientation sampling for dictionary-based diffraction pattern indexing methods. Modelling and Simulation in Materials Science and Engineering 24(8), 085013 (2016)
Singh, S., De Graef, M.: Dictionary indexing of electron channeling patterns. Microsc. MicroAnal. 23, 1--12 (2017)
Singh, S., Guo, Y., Winiarski, B., Burnett, T., Withers, P., De Graef, M.: High resolution low kv EBSD of heavily deformed and nanocrystalline Aluminium by dictionary-based indexing. Nature Scientific Reports 8, 10991 (2018)
Smyth, J., Hazen, R.: The crystal structures of Forsterite and Hortonolite at several temperatures up to $900^{\circ}$C. Amer. Mineral. 58, 588--593 (1973)
Uchic, M., Groeber, M., Shahi, M., Callahan, P., Shiveley, A., Scott, M., Chapman, M., Spowart, J.: An automated multi-modal serial sectioning system for characterization of grain-scale microstructures in engineering materials. In: M. De Graef, H. Poulsen, A. Lewis, J. Simmons, G. Spanos (eds.) Proc. 1st Int. Conf. on 3D Materials Science, pp. 195--202. Springer, Cham (2012)
Vespucci, S., Winkelmann, A., Naresh-Kumar, G., Mingard, K.P., Maneuski, D., Edwards, P.R., Day, A.P., O'Shea, V., Trager-Cowan, C.: Digital direct electron imaging of energy-filtered electron backscatter diffraction patterns. Physical Review B 92(20), 205301 (2015)
Villars, P.: Pearson's Handbook (Desk Edition) Crystallographic Data for Intermetallic Phases. American Society for Metals (1997)
Wang, A., De Graef, M.: Modeling dynamical electron scattering with Bethe potentials and the scattering matrix. Ultramicroscopy 160, 35--43 (2016)
Wilkinson, A.J., Moldovan, G., Britton, T.B., Bewick, A., Clough, R., Kirkland, A.I.: Direct detection of electron backscatter diffraction patterns. Physical review letters 111(6), 065506 (2013)
Winkelmann, A., Britton, T.B., Nolze, G.: Constraints on the effective electron energy spectrum in backscatter kikuchi diffraction. Phys. Rev. B 99, 064115 (2019)
Wright, S.I., Nowell, M.M., Lindeman, S.P., Camus, P.P., De Graef, M., Jackson, M.A.: Introduction and comparison of new ebsd post-processing methodologies. Ultramicroscopy 159, 81--94 (2015).
Wiki pages are maintained by M. De Graef; they are part of the EMsoft package and fall under the same copyright (BSD2).
Information for Users
SEM Modalities
- Monte Carlo Simulations- EBSD Master Pattern Simulations
- EBSD Overlap Master Patterns
- EBSD Pattern Simulations
- EBSD Dictionary Indexing
- EBSD Spherical Indexing
- EBSD Reflector Ranking
- EBSD HREBSD
- ECP Master Pattern Simulations
- ECP Pattern Simulations
- TKD Master Pattern Simulations
- TKD Pattern Simulations
- ECCI Defect Image Simulations
TEM Modalities
- HH4- PED
- CBED Pattern Simulations
- STEM-DCI Image Simulations
- EMIntegrateSTEM utility
Utility Programs
- EMConvertOrientations- EMDisorientations
- EMHOLZ
- EMKikuchiMap
- EMOpenCLinfo
- EMZAgeom
- EMcuboMK
- EMdpextract
- EMdpmerge
- EMdrawcell
- EMeqvPS
- EMeqvrot
- EMfamily
- EMGBO
- EMGBOdm
- EMgetEulers
- EMgetOSM
- EMlatgeom
- EMlistSG
- EMlistTC
- EMmkxtal
- EMorbit
- EMorient
- EMqg
- EMsampleRFZ
- EMshowxtal
- EMsoftSlackTest
- EMsoftinit
- EMstar
- EMstereo
- EMxtalExtract
- EMxtalinfo
- EMzap
Complete Examples
- Crystal Data Entry Example
- EBSD Example
- ECP Example
- TKD Example
- ECCI Example
- CBED Example
- Dictionary Indexing Example
- DItutorial
Information for Developers