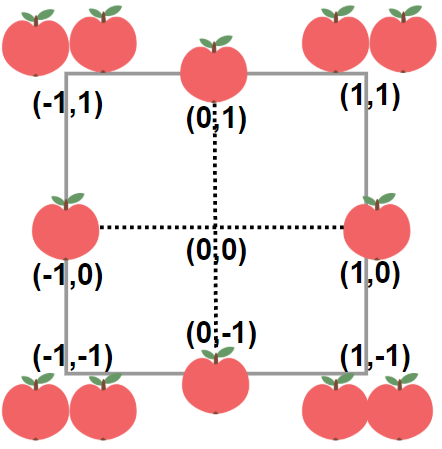
In a garden represented as an infinite 2D grid, there is an apple tree planted at every integer coordinate. The apple tree planted at an integer coordinate (i, j) has |i| + |j| apples growing on it.
You will buy an axis-aligned square plot of land that is centered at (0, 0).
Given an integer neededApples, return the minimum perimeter of a plot such that at least neededApples apples are inside or on the perimeter of that plot.
The value of |x| is defined as:
xifx >= 0-xifx < 0
Example 1:
Input: neededApples = 1 Output: 8 Explanation: A square plot of side length 1 does not contain any apples. However, a square plot of side length 2 has 12 apples inside (as depicted in the image above). The perimeter is 2 * 4 = 8.
Example 2:
Input: neededApples = 13 Output: 16
Example 3:
Input: neededApples = 1000000000 Output: 5040
Constraints:
1 <= neededApples <= 1015
class Solution:
def minimumPerimeter(self, neededApples: int) -> int:
x = 1
while 2 * x * (x + 1) * (2 * x + 1) < neededApples:
x += 1
return x * 8class Solution:
def minimumPerimeter(self, neededApples: int) -> int:
l, r = 1, 100000
while l < r:
mid = (l + r) >> 1
if 2 * mid * (mid + 1) * (2 * mid + 1) >= neededApples:
r = mid
else:
l = mid + 1
return l * 8class Solution {
public long minimumPerimeter(long neededApples) {
long x = 1;
while (2 * x * (x + 1) * (2 * x + 1) < neededApples) {
++x;
}
return 8 * x;
}
}class Solution {
public long minimumPerimeter(long neededApples) {
long l = 1, r = 100000;
while (l < r) {
long mid = (l + r) >> 1;
if (2 * mid * (mid + 1) * (2 * mid + 1) >= neededApples) {
r = mid;
} else {
l = mid + 1;
}
}
return l * 8;
}
}class Solution {
public:
long long minimumPerimeter(long long neededApples) {
long long x = 1;
while (2 * x * (x + 1) * (2 * x + 1) < neededApples) {
++x;
}
return 8 * x;
}
};class Solution {
public:
long long minimumPerimeter(long long neededApples) {
long long l = 1, r = 100000;
while (l < r) {
long mid = (l + r) >> 1;
if (2 * mid * (mid + 1) * (2 * mid + 1) >= neededApples) {
r = mid;
} else {
l = mid + 1;
}
}
return l * 8;
}
};func minimumPerimeter(neededApples int64) int64 {
var x int64 = 1
for 2*x*(x+1)*(2*x+1) < neededApples {
x++
}
return 8 * x
}func minimumPerimeter(neededApples int64) int64 {
var l, r int64 = 1, 100000
for l < r {
mid := (l + r) >> 1
if 2*mid*(mid+1)*(2*mid+1) >= neededApples {
r = mid
} else {
l = mid + 1
}
}
return l * 8
}function minimumPerimeter(neededApples: number): number {
let x = 1;
while (2 * x * (x + 1) * (2 * x + 1) < neededApples) {
++x;
}
return 8 * x;
}function minimumPerimeter(neededApples: number): number {
let l = 1;
let r = 100000;
while (l < r) {
const mid = (l + r) >> 1;
if (2 * mid * (mid + 1) * (2 * mid + 1) >= neededApples) {
r = mid;
} else {
l = mid + 1;
}
}
return 8 * l;
}