---

Introduction

MEALPY is the largest python library in the world for most of the cutting-edge meta-heuristic algorithms (nature-inspired algorithms, black-box optimization, global search optimizers, iterative learning algorithms, continuous optimization, derivative free optimization, gradient free optimization, zeroth order optimization, stochastic search optimization, random search optimization). These algorithms belong to population-based algorithms (PMA), which are the most popular algorithms in the field of approximate optimization.

• Free software: GNU General Public License (GPL) V3 license
• Total algorithms: 215 (190 official (original, hybrid, variants), 25 developed)
• Documentation: https://mealpy.readthedocs.io/en/latest/
• Python versions: >=3.7x
• Dependencies: numpy, scipy, pandas, matplotlib

Citation Request

Please include these citations if you plan to use this library:

@article{van2023mealpy,
  title={MEALPY: An open-source library for latest meta-heuristic algorithms in Python},
  author={Van Thieu, Nguyen and Mirjalili, Seyedali},
  journal={Journal of Systems Architecture},
  year={2023},
  publisher={Elsevier},
  doi={10.1016/j.sysarc.2023.102871}
}

@article{van2023groundwater,
  title={Groundwater level modeling using Augmented Artificial Ecosystem Optimization},
  author={Van Thieu, Nguyen and Barma, Surajit Deb and Van Lam, To and Kisi, Ozgur and Mahesha, Amai},
  journal={Journal of Hydrology},
  volume={617},
  pages={129034},
  year={2023},
  publisher={Elsevier},
  doi={https://doi.org/10.1016/j.jhydrol.2022.129034}
}

@article{ahmed2021comprehensive,
  title={A comprehensive comparison of recent developed meta-heuristic algorithms for streamflow time series forecasting problem},
  author={Ahmed, Ali Najah and Van Lam, To and Hung, Nguyen Duy and Van Thieu, Nguyen and Kisi, Ozgur and El-Shafie, Ahmed},
  journal={Applied Soft Computing},
  volume={105},
  pages={107282},
  year={2021},
  publisher={Elsevier},
  doi={10.1016/j.asoc.2021.107282}
}

Usage

Goals

Our goals are to implement all classical as well as the state-of-the-art nature-inspired algorithms, create a simple interface that helps researchers access optimization algorithms as quickly as possible, and share knowledge of the optimization field with everyone without a fee. What you can do with mealpy:

• Analyse parameters of meta-heuristic algorithms.
• Perform Qualitative and Quantitative Analysis of algorithms.
• Analyse rate of convergence of algorithms.
• Test and Analyse the scalability and the robustness of algorithms.
• Save results in various formats (csv, json, pickle, png, pdf, jpeg)
• Export and import models can also be done with Mealpy.
• Solve any optimization problem

Installation

• Install the stable (latest) version from PyPI release:

$ pip install mealpy==3.0.1

• Install the alpha/beta version from PyPi

$ pip install mealpy==2.5.4a6

• Install the pre-release version directly from the source code:

$ git clone https://github.com/thieu1995/mealpy.git
$ cd mealpy
$ python setup.py install

• In case, you want to install the development version from Github:

$ pip install git+https://github.com/thieu1995/permetrics 

After installation, you can import Mealpy as any other Python module:

$ python
>>> import mealpy
>>> mealpy.__version__

>>> print(mealpy.get_all_optimizers())
>>> model = mealpy.get_optimizer_by_name("OriginalWOA")(epoch=100, pop_size=50)

Examples

Before dive into some examples, let me ask you a question. What type of problem are you trying to solve? Additionally, what would be the solution for your specific problem? Based on the table below, you can select an appropriate type of decision variables to use.

Class	Syntax	Problem Types
FloatVar	FloatVar(lb=(-10., )*7, ub=(10., )*7, name="delta")	Continuous Problem
IntegerVar	IntegerVar(lb=(-10., )*7, ub=(10., )*7, name="delta")	LP, IP, NLP, QP, MIP
StringVar	StringVar(valid_sets=(("auto", "backward", "forward"), ("leaf", "branch", "root")), name="delta")	ML, AI-optimize
BinaryVar	BinaryVar(n_vars=11, name="delta")	Networks
BoolVar	BoolVar(n_vars=11, name="delta")	ML, AI-optimize
PermutationVar	PermutationVar(valid_set=(-10, -4, 10, 6, -2), name="delta")	Combinatorial Optimization
MixedSetVar	MixedSetVar(valid_sets=(("auto", 2, 3, "backward", True), (0, "tournament", "round-robin")), name="delta")	MIP, MILP
TransferBoolVar	TransferBoolVar(n_vars=11, name="delta", tf_func="sstf_02")	ML, AI-optimize, Feature
TransferBinaryVar	TransferBinaryVar(n_vars=11, name="delta", tf_func="vstf_04")	Networks, Feature Selection

Let's go through a basic and advanced example.

Simple Benchmark Function

Using Problem dict

from mealpy import FloatVar, SMA
import numpy as np

def objective_function(solution):
    return np.sum(solution**2)

problem = {
    "obj_func": objective_function,
    "bounds": FloatVar(lb=(-100., )*30, ub=(100., )*30),
    "minmax": "min",
    "log_to": None,
}

## Run the algorithm
model = SMA.OriginalSMA(epoch=100, pop_size=50, pr=0.03)
g_best = model.solve(problem)
print(f"Best solution: {g_best.solution}, Best fitness: {g_best.target.fitness}")

Define a custom Problem class

Please note that, there is no more generate_position, amend_solution, and fitness_function in Problem class. We take care everything under the DataType Class above. Just choose which one fit for your problem. We recommend you define a custom class that inherit Problem class if your decision variable is not FloatVar

from mealpy import Problem, FloatVar, BBO 
import numpy as np

# Our custom problem class
class Squared(Problem):
    def __init__(self, bounds=None, minmax="min", data=None, **kwargs):
        self.data = data 
        super().__init__(bounds, minmax, **kwargs)

    def obj_func(self, solution):
        x = self.decode_solution(solution)["my_var"]
        return np.sum(x ** 2)

## Now, we define an algorithm, and pass an instance of our *Squared* class as the problem argument. 
bound = FloatVar(lb=(-10., )*20, ub=(10., )*20, name="my_var")
problem = Squared(bounds=bound, minmax="min", name="Squared", data="Amazing")
model = BBO.OriginalBBO(epoch=100, pop_size=20)
g_best = model.solve(problem)

Set Seed for Optimizer (So many people asking for this feature)

You can set random seed number for each run of single optimizer.

model = SMA.OriginalSMA(epoch=100, pop_size=50, pr=0.03)
g_best = model.solve(problem=problem, seed=10)  # Default seed=None

Large-Scale Optimization

from mealpy import FloatVar, SHADE
import numpy as np

def objective_function(solution):
    return np.sum(solution**2)

problem = {
    "obj_func": objective_function,
    "bounds": FloatVar(lb=(-1000., )*10000, ub=(1000.,)*10000),     # 10000 dimensions
    "minmax": "min",
    "log_to": "console",
}

## Run the algorithm
optimizer = SHADE.OriginalSHADE(epoch=10000, pop_size=100)
g_best = optimizer.solve(problem)
print(f"Best solution: {g_best.solution}, Best fitness: {g_best.target.fitness}")

Distributed Optimization / Parallelization Optimization

Please read the article titled MEALPY: An open-source library for latest meta-heuristic algorithms in Python to gain a clear understanding of the concept of parallelization (distributed optimization) in metaheuristics. Not all metaheuristics can be run in parallel.

from mealpy import FloatVar, SMA
import numpy as np


def objective_function(solution):
    return np.sum(solution**2)

problem = {
    "obj_func": objective_function,
    "bounds": FloatVar(lb=(-100., )*100, ub=(100., )*100),
    "minmax": "min",
    "log_to": "console",
}

## Run distributed SMA algorithm using 10 threads
optimizer = SMA.OriginalSMA(epoch=10000, pop_size=100, pr=0.03)
optimizer.solve(problem, mode="thread", n_workers=10)        # Distributed to 10 threads
print(f"Best solution: {optimizer.g_best.solution}, Best fitness: {optimizer.g_best.target.fitness}")

## Run distributed SMA algorithm using 8 CPUs (cores)
optimizer.solve(problem, mode="process", n_workers=8)        # Distributed to 8 cores
print(f"Best solution: {optimizer.g_best.solution}, Best fitness: {optimizer.g_best.target.fitness}")

The Benefit Of Using Custom Problem Class (BEST PRACTICE)

Optimize Machine Learning model

In this example, we use SMA optimize to optimize the hyper-parameters of SVC model.

from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn import datasets, metrics

from mealpy import FloatVar, StringVar, IntegerVar, BoolVar, MixedSetVar, SMA, Problem


# Load the data set; In this example, the breast cancer dataset is loaded.
X, y = datasets.load_breast_cancer(return_X_y=True)

# Create training and test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)

sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)

data = {
    "X_train": X_train_std,
    "X_test": X_test_std,
    "y_train": y_train,
    "y_test": y_test
}


class SvmOptimizedProblem(Problem):
    def __init__(self, bounds=None, minmax="max", data=None, **kwargs):
        self.data = data
        super().__init__(bounds, minmax, **kwargs)

    def obj_func(self, x):
        x_decoded = self.decode_solution(x)
        C_paras, kernel_paras = x_decoded["C_paras"], x_decoded["kernel_paras"]
        degree, gamma, probability = x_decoded["degree_paras"], x_decoded["gamma_paras"], x_decoded["probability_paras"]

        svc = SVC(C=C_paras, kernel=kernel_paras, degree=degree, 
                  gamma=gamma, probability=probability, random_state=1)
        # Fit the model
        svc.fit(self.data["X_train"], self.data["y_train"])
        # Make the predictions
        y_predict = svc.predict(self.data["X_test"])
        # Measure the performance
        return metrics.accuracy_score(self.data["y_test"], y_predict)

my_bounds = [
    FloatVar(lb=0.01, ub=1000., name="C_paras"),
    StringVar(valid_sets=('linear', 'poly', 'rbf', 'sigmoid'), name="kernel_paras"),
    IntegerVar(lb=1, ub=5, name="degree_paras"),
    MixedSetVar(valid_sets=('scale', 'auto', 0.01, 0.05, 0.1, 0.5, 1.0), name="gamma_paras"),
    BoolVar(n_vars=1, name="probability_paras"),
]
problem = SvmOptimizedProblem(bounds=my_bounds, minmax="max", data=data)
model = SMA.OriginalSMA(epoch=100, pop_size=20)
model.solve(problem)

print(f"Best agent: {model.g_best}")
print(f"Best solution: {model.g_best.solution}")
print(f"Best accuracy: {model.g_best.target.fitness}")
print(f"Best parameters: {model.problem.decode_solution(model.g_best.solution)}")

Solving Combinatorial Problems

Traveling Salesman Problem (TSP)

In the context of the Mealpy for the Traveling Salesman Problem (TSP), a solution is a possible route that represents a tour of visiting all the cities exactly once and returning to the starting city. The solution is typically represented as a permutation of the cities, where each city appears exactly once in the permutation.

For example, let's consider a TSP instance with 5 cities labeled as A, B, C, D, and E. A possible solution could be represented as the permutation [A, B, D, E, C], which indicates the order in which the cities are visited. This solution suggests that the tour starts at city A, then moves to city B, then D, E, and finally C before returning to city A.

import numpy as np
from mealpy import PermutationVar, WOA, Problem

# Define the positions of the cities
city_positions = np.array([[60, 200], [180, 200], [80, 180], [140, 180], [20, 160],
                           [100, 160], [200, 160], [140, 140], [40, 120], [100, 120],
                           [180, 100], [60, 80], [120, 80], [180, 60], [20, 40],
                           [100, 40], [200, 40], [20, 20], [60, 20], [160, 20]])
num_cities = len(city_positions)
data = {
    "city_positions": city_positions,
    "num_cities": num_cities,
}

class TspProblem(Problem):
    def __init__(self, bounds=None, minmax="min", data=None, **kwargs):
        self.data = data
        super().__init__(bounds, minmax, **kwargs)

    @staticmethod
    def calculate_distance(city_a, city_b):
        # Calculate Euclidean distance between two cities
        return np.linalg.norm(city_a - city_b)

    @staticmethod
    def calculate_total_distance(route, city_positions):
        # Calculate total distance of a route
        total_distance = 0
        num_cities = len(route)
        for idx in range(num_cities):
            current_city = route[idx]
            next_city = route[(idx + 1) % num_cities]  # Wrap around to the first city
            total_distance += TspProblem.calculate_distance(city_positions[current_city], city_positions[next_city])
        return total_distance

    def obj_func(self, x):
        x_decoded = self.decode_solution(x)
        route = x_decoded["per_var"]
        fitness = self.calculate_total_distance(route, self.data["city_positions"])
        return fitness


bounds = PermutationVar(valid_set=list(range(0, num_cities)), name="per_var")
problem = TspProblem(bounds=bounds, minmax="min", data=data)

model = WOA.OriginalWOA(epoch=100, pop_size=20)
model.solve(problem)

print(f"Best agent: {model.g_best}")                    # Encoded solution
print(f"Best solution: {model.g_best.solution}")        # Encoded solution
print(f"Best fitness: {model.g_best.target.fitness}")
print(f"Best real scheduling: {model.problem.decode_solution(model.g_best.solution)}")      # Decoded (Real) solution

Job Shop Scheduling Problem Using Woa Optimizer

Note that this implementation assumes that the job times and machine times are provided as 2D lists, where job_times[i][j] represents the processing time of job i on machine j.

Keep in mind that this is a simplified implementation, and you may need to modify it according to the specific requirements and constraints of your Job Shop Scheduling problem.

import numpy as np
from mealpy import PermutationVar, WOA, Problem


job_times = [[2, 1, 3], [4, 2, 1], [3, 3, 2]]
machine_times = [[3, 2, 1], [1, 4, 2], [2, 3, 2]]

n_jobs = len(job_times)
n_machines = len(machine_times)

data = {
    "job_times": job_times,
    "machine_times": machine_times,
    "n_jobs": n_jobs,
    "n_machines": n_machines
}

class JobShopProblem(Problem):
    def __init__(self, bounds=None, minmax="min", data=None, **kwargs):
        self.data = data
        super().__init__(bounds, minmax, **kwargs)

    def obj_func(self, x):
        x_decoded = self.decode_solution(x)
        x = x_decoded["per_var"]
        makespan = np.zeros((self.data["n_jobs"], self.data["n_machines"]))
        for gene in x:
            job_idx = gene // self.data["n_machines"]
            machine_idx = gene % self.data["n_machines"]
            if job_idx == 0 and machine_idx == 0:
                makespan[job_idx][machine_idx] = job_times[job_idx][machine_idx]
            elif job_idx == 0:
                makespan[job_idx][machine_idx] = makespan[job_idx][machine_idx - 1] + job_times[job_idx][machine_idx]
            elif machine_idx == 0:
                makespan[job_idx][machine_idx] = makespan[job_idx - 1][machine_idx] + job_times[job_idx][machine_idx]
            else:
                makespan[job_idx][machine_idx] = max(makespan[job_idx][machine_idx - 1], makespan[job_idx - 1][machine_idx]) + job_times[job_idx][machine_idx]
        return np.max(makespan)


bounds = PermutationVar(valid_set=list(range(0, n_jobs*n_machines)), name="per_var")
problem = JobShopProblem(bounds=bounds, minmax="min", data=data)

model = WOA.OriginalWOA(epoch=100, pop_size=20)
model.solve(problem)

print(f"Best agent: {model.g_best}")                    # Encoded solution
print(f"Best solution: {model.g_best.solution}")        # Encoded solution
print(f"Best fitness: {model.g_best.target.fitness}")
print(f"Best real scheduling: {model.problem.decode_solution(model.g_best.solution)}")      # Decoded (Real) solution

Shortest Path Problem

In this example, the graph is represented as a NumPy array where each element represents the cost or distance between two nodes.

Note that this implementation assumes that the graph is represented by a symmetric matrix, where graph[i,j] represents the distance between nodes i and j. If your graph representation is different, you may need to modify the code accordingly.

Please keep in mind that this implementation is a basic example and may not be optimized for large-scale problems. Further modifications and optimizations may be required depending on your specific use case.

import numpy as np
from mealpy import PermutationVar, WOA, Problem

# Define the graph representation
graph = np.array([
    [0, 2, 4, 0, 7, 9],
    [2, 0, 1, 4, 2, 8],
    [4, 1, 0, 1, 3, 0],
    [6, 4, 5, 0, 3, 2],
    [0, 2, 3, 3, 0, 2],
    [9, 0, 4, 2, 2, 0]
])


class ShortestPathProblem(Problem):
    def __init__(self, bounds=None, minmax="min", data=None, **kwargs):
        self.data = data
        self.eps = 1e10         # Penalty function for vertex with 0 connection
        super().__init__(bounds, minmax, **kwargs)

    # Calculate the fitness of an individual
    def obj_func(self, x):
        x_decoded = self.decode_solution(x)
        individual = x_decoded["path"]

        total_distance = 0
        for idx in range(len(individual) - 1):
            start_node = individual[idx]
            end_node = individual[idx + 1]
            weight = self.data[start_node, end_node]
            if weight == 0:
                return self.eps
            total_distance += weight
        return total_distance


num_nodes = len(graph)
bounds = PermutationVar(valid_set=list(range(0, num_nodes)), name="path")
problem = ShortestPathProblem(bounds=bounds, minmax="min", data=graph)

model = WOA.OriginalWOA(epoch=100, pop_size=20)
model.solve(problem)

print(f"Best agent: {model.g_best}")                    # Encoded solution
print(f"Best solution: {model.g_best.solution}")        # Encoded solution
print(f"Best fitness: {model.g_best.target.fitness}")
print(f"Best real scheduling: {model.problem.decode_solution(model.g_best.solution)}")      # Decoded (Real) solution

Location Optimization

Let's consider an example of location optimization in the context of a retail company that wants to open a certain number of new stores in a region to maximize market coverage while minimizing operational costs.

A company wants to open five new stores in a region with several potential locations. The objective is to determine the optimal locations for these stores while considering factors such as population density and transportation costs. The goal is to maximize market coverage by locating stores in areas with high demand while minimizing the overall transportation costs required to serve customers.

By applying location optimization techniques, the retail company can make informed decisions about where to open new stores, considering factors such as population density and transportation costs. This approach allows the company to maximize market coverage, make efficient use of resources, and ultimately improve customer service and profitability.

Note that this example is a simplified illustration, and in real-world scenarios, location optimization problems can involve more complex constraints, additional factors, and larger datasets. However, the general process remains similar, involving data analysis, mathematical modeling, and optimization techniques to determine the optimal locations for facilities.

import numpy as np
from mealpy import BinaryVar, WOA, Problem

# Define the coordinates of potential store locations
locations = np.array([
    [2, 4],
    [5, 6],
    [9, 3],
    [7, 8],
    [1, 10],
    [3, 2],
    [5, 5],
    [8, 2],
    [7, 6],
    [1, 9]
])
# Define the transportation costs matrix based on the Euclidean distance between locations
distance_matrix = np.linalg.norm(locations[:, np.newaxis] - locations, axis=2)

# Define the number of stores to open
num_stores = 5

# Define the maximum distance a customer should travel to reach a store
max_distance = 10

data = {
    "num_stores": num_stores,
    "max_distance": max_distance,
    "penalty": 1e10
}


class LocationOptProblem(Problem):
    def __init__(self, bounds=None, minmax=None, data=None, **kwargs):
        self.data = data
        self.eps = 1e10
        super().__init__(bounds, minmax, **kwargs)

    # Define the fitness evaluation function
    def obj_func(self, x):
        x_decoded = self.decode_solution(x)
        x = x_decoded["placement_var"]
        total_coverage = np.sum(x)
        total_dist = np.sum(x[:, np.newaxis] * distance_matrix)
        if total_dist == 0:                 # Penalize solutions with fewer stores
            return self.eps
        if total_coverage < self.data["num_stores"]:    # Penalize solutions with fewer stores
            return self.eps
        return total_dist


bounds = BinaryVar(n_vars=len(locations), name="placement_var")
problem = LocationOptProblem(bounds=bounds, minmax="min", data=data)

model = WOA.OriginalWOA(epoch=50, pop_size=20)
model.solve(problem)

print(f"Best agent: {model.g_best}")                    # Encoded solution
print(f"Best solution: {model.g_best.solution}")        # Encoded solution
print(f"Best fitness: {model.g_best.target.fitness}")
print(f"Best real scheduling: {model.problem.decode_solution(model.g_best.solution)}")      # Decoded (Real) solution

Supply Chain Optimization

Let's assume we have a supply chain network with 5 distribution centers (DC1, DC2, DC3, DC4, DC5) and 10 products (P1, P2, P3, ..., P10). Our goal is to determine the optimal allocation of products to the distribution centers in a way that minimizes the total transportation cost.

Each solution represents an allocation of products to distribution centers. We can use a binary matrix with dimensions (10, 5) where each element (i, j) represents whether product i is allocated to distribution center j. For example, a chromosome [1, 0, 1, 0, 1] would mean that product 1 is allocated to DC1, DC3, DC5.

We can add the maximum capacity of each distribution center, therefor we need penalty term to the fitness evaluation function to penalize solutions that violate this constraint. The penalty can be based on the degree of violation or a fixed penalty value.

import numpy as np
from mealpy import BinaryVar, WOA, Problem

# Define the problem parameters
num_products = 10
num_distribution_centers = 5

# Define the transportation cost matrix (randomly generated for the example)
transportation_cost = np.random.randint(1, 10, size=(num_products, num_distribution_centers))

data = {
    "num_products": num_products,
    "num_distribution_centers": num_distribution_centers,
    "transportation_cost": transportation_cost,
    "max_capacity": 4,      # Maximum capacity of each distribution center
    "penalty": 1e10         # Define a penalty value for maximum capacity of each distribution center
}


class SupplyChainProblem(Problem):
    def __init__(self, bounds=None, minmax=None, data=None, **kwargs):
        self.data = data
        super().__init__(bounds, minmax, **kwargs)

    def obj_func(self, x):
        x_decoded = self.decode_solution(x)
        x = x_decoded["placement_var"].reshape((self.data["num_products"], self.data["num_distribution_centers"]))

        if np.any(np.all(x==0, axis=1)):    
        # If any row has all 0 value, it indicates that this product is not allocated to any distribution center.
            return 0

        total_cost = np.sum(self.data["transportation_cost"] * x)
        # Penalty for violating maximum capacity constraint
        excess_capacity = np.maximum(np.sum(x, axis=0) - self.data["max_capacity"], 0)
        penalty = np.sum(excess_capacity)
        # Calculate fitness value as the inverse of the total cost plus the penalty
        fitness = 1 / (total_cost + penalty)
        return fitness


bounds = BinaryVar(n_vars=num_products * num_distribution_centers, name="placement_var")
problem = SupplyChainProblem(bounds=bounds, minmax="max", data=data)

model = WOA.OriginalWOA(epoch=50, pop_size=20)
model.solve(problem)

print(f"Best agent: {model.g_best}")                    # Encoded solution
print(f"Best solution: {model.g_best.solution}")        # Encoded solution
print(f"Best fitness: {model.g_best.target.fitness}")
print(f"Best real scheduling: {model.problem.decode_solution(model.g_best.solution)['placement_var'].reshape((num_products, num_distribution_centers))}")

Healthcare Workflow Optimization Problem

Define a chromosome representation that encodes the allocation of resources and patient flow in the emergency department. This could be a binary matrix where each row represents a patient and each column represents a resource (room). If the element is 1, it means the patient is assigned to that particular room, and if the element is 0, it means the patient is not assigned to that room

Please note that this implementation is a basic template and may require further customization based on the specific objectives, constraints, and evaluation criteria of your healthcare workflow optimization problem. You'll need to define the specific fitness function and optimization objectives based on the factors you want to optimize, such as patient waiting times, resource utilization, and other relevant metrics in the healthcare workflow context.

import numpy as np
from mealpy import BinaryVar, WOA, Problem

# Define the problem parameters
num_patients = 50  # Number of patients
num_resources = 10  # Number of resources (room)

# Define the patient waiting time matrix (randomly generated for the example)
# Why? May be, doctors need time to prepare tools,...
waiting_matrix = np.random.randint(1, 10, size=(num_patients, num_resources))

data = {
    "num_patients": num_patients,
    "num_resources": num_resources,
    "waiting_matrix": waiting_matrix,
    "max_resource_capacity": 10,        # Maximum capacity of each room
    "max_waiting_time": 60,             # Maximum waiting time
    "penalty_value": 1e2,         # Define a penalty value
    "penalty_patient": 1e10
}


class SupplyChainProblem(Problem):
    def __init__(self, bounds=None, minmax=None, data=None, **kwargs):
        self.data = data
        super().__init__(bounds, minmax, **kwargs)

    def obj_func(self, x):
        x_decoded = self.decode_solution(x)
        x = x_decoded["placement_var"].reshape(self.data["num_patients"], self.data["num_resources"])

        # If any row has all 0 value, it indicates that this patient is not allocated to any room.
        # If a patient a assigned to more than 3 room, not allow
        if np.any(np.all(x==0, axis=1)) or np.any(np.sum(x>3, axis=1)):
            return self.data["penalty_patient"]

        # Calculate fitness based on optimization objectives
        room_used = np.sum(x, axis=0)
        wait_time = np.sum(x * self.data["waiting_matrix"], axis=1)
        violated_constraints = np.sum(room_used > self.data["max_resource_capacity"]) + np.sum(wait_time > self.data["max_waiting_time"])

        # Calculate the fitness value based on the objectives
        resource_utilization_fitness = 1 - np.mean(room_used) / self.data["max_resource_capacity"]
        waiting_time_fitness = 1 - np.mean(wait_time) / self.data["max_waiting_time"]

        fitness = resource_utilization_fitness + waiting_time_fitness + self.data['penalty_value'] * violated_constraints
        return fitness


bounds = BinaryVar(n_vars=num_patients * num_resources, name="placement_var")
problem = SupplyChainProblem(bounds=bounds, minmax="min", data=data)

model = WOA.OriginalWOA(epoch=50, pop_size=20)
model.solve(problem)

print(f"Best agent: {model.g_best}")                    # Encoded solution
print(f"Best solution: {model.g_best.solution}")        # Encoded solution
print(f"Best fitness: {model.g_best.target.fitness}")
print(f"Best real scheduling: {model.problem.decode_solution(model.g_best.solution)['placement_var'].reshape((num_patients, num_resources))}")

Production Optimization Problem

Let's consider a simplified example of production optimization in the context of a manufacturing company that produces electronic devices, such as smartphones. The objective is to maximize production output while minimizing production costs.

This example uses binary representations for production configurations, assuming each task can be assigned to a resource (1) or not (0). You may need to adapt the representation and operators to suit your specific production optimization problem.

import numpy as np
from mealpy import BinaryVar, WOA, Problem

# Define the problem parameters
num_tasks = 10
num_resources = 5

# Example task processing times
task_processing_times = np.array([2, 3, 4, 2, 3, 2, 3, 4, 2, 3])

# Example resource capacity
resource_capacity = np.array([10, 8, 6, 12, 15])

# Example production costs and outputs
production_costs = np.array([5, 6, 4, 7, 8, 9, 5, 6, 7, 8])
production_outputs = np.array([20, 18, 16, 22, 25, 24, 20, 18, 19, 21])

# Example maximum total production time
max_total_time = 50

# Example maximum defect rate
max_defect_rate = 0.2

# Penalty for invalid solution
penalty = -1000

data = {
    "num_tasks": num_tasks,
    "num_resources": num_resources,
    "task_processing_times": task_processing_times,
    "resource_capacity": resource_capacity,
    "production_costs": production_costs,
    "production_outputs": production_outputs,
    "max_defect_rate": max_defect_rate,
    "penalty": penalty
}


class SupplyChainProblem(Problem):
    def __init__(self, bounds=None, minmax=None, data=None, **kwargs):
        self.data = data
        super().__init__(bounds, minmax, **kwargs)

    def obj_func(self, x):
        x_decoded = self.decode_solution(x)
        x = x_decoded["placement_var"].reshape((self.data["num_tasks"], self.data["num_resources"]))

        # If any row has all 0 value, it indicates that this task is not allocated to any resource
        if np.any(np.all(x==0, axis=1)) or np.any(np.all(x==0, axis=0)):
            return self.data["penalty"]

        # Check violated constraints
        violated_constraints = 0

        # Calculate resource utilization
        resource_utilization = np.sum(x, axis=0)
        # Resource capacity constraint
        if np.any(resource_utilization > self.data["resource_capacity"]):
            violated_constraints += 1

        # Time constraint
        total_time = np.sum(np.dot(self.data["task_processing_times"].reshape(1, -1), x))
        if total_time > max_total_time:
            violated_constraints += 1

        # Quality constraint
        defect_rate = np.dot(self.data["production_costs"].reshape(1, -1), x) / np.dot(self.data["production_outputs"], x)
        if np.any(defect_rate > max_defect_rate):
            violated_constraints += 1

        # Calculate the fitness value based on the objectives and constraints
        profit = np.sum(np.dot(self.data["production_outputs"].reshape(1, -1), x)) - np.sum(np.dot(self.data["production_costs"].reshape(1, -1), x))
        if violated_constraints > 0:
            return profit + self.data["penalty"] * violated_constraints       # Penalize solutions with violated constraints
        return profit


bounds = BinaryVar(n_vars=num_tasks * num_resources, name="placement_var")
problem = SupplyChainProblem(bounds=bounds, minmax="max", data=data)

model = WOA.OriginalWOA(epoch=50, pop_size=20)
model.solve(problem)

print(f"Best agent: {model.g_best}")                    # Encoded solution
print(f"Best solution: {model.g_best.solution}")        # Encoded solution
print(f"Best fitness: {model.g_best.target.fitness}")
print(f"Best real scheduling: {model.problem.decode_solution(model.g_best.solution)['placement_var'].reshape((num_tasks, num_resources))}")

Employee Rostering Problem Using Woa Optimizer

The goal is to create an optimal schedule that assigns employees to shifts while satisfying various constraints and objectives. Note that this implementation assumes that shift_requirements array has dimensions (num_employees, num_shifts), and shift_costs is a 1D array of length num_shifts.

Please keep in mind that this is a simplified implementation, and you may need to modify it according to the specific requirements and constraints of your employee rostering problem. Additionally, you might want to introduce additional mechanisms or constraints such as fairness, employee preferences, or shift dependencies to enhance the model's effectiveness in real-world scenarios.

For example, if you have 5 employees and 3 shifts, a chromosome could be represented as [2, 1, 0, 2, 0], where employee 0 is assigned to shift 2, employee 1 is assigned to shift 1, employee 2 is assigned to shift 0, and so on.

import numpy as np
from mealpy import IntegerVar, WOA, Problem


shift_requirements = np.array([[2, 1, 3], [4, 2, 1], [3, 3, 2]])
shift_costs = np.array([10, 8, 12])

num_employees = shift_requirements.shape[0]
num_shifts = shift_requirements.shape[1]

data = {
    "shift_requirements": shift_requirements,
    "shift_costs": shift_costs,
    "num_employees": num_employees,
    "num_shifts": num_shifts
}

class EmployeeRosteringProblem(Problem):
    def __init__(self, bounds=None, minmax="min", data=None, **kwargs):
        self.data = data
        super().__init__(bounds, minmax, **kwargs)

    def obj_func(self, x):
        x_decoded = self.decode_solution(x)
        x = x_decoded["shift_var"]

        shifts_covered = np.zeros(self.data["num_shifts"])
        total_cost = 0
        for idx in range(self.data["num_employees"]):
            shift_idx = x[idx]
            shifts_covered[shift_idx] += 1
            total_cost += self.data["shift_costs"][shift_idx]
        coverage_diff = self.data["shift_requirements"] - shifts_covered
        coverage_penalty = np.sum(np.abs(coverage_diff))
        return total_cost + coverage_penalty


bounds = IntegerVar(lb=[0, ]*num_employees, ub=[num_shifts-1, ]*num_employees, name="shift_var")
problem = EmployeeRosteringProblem(bounds=bounds, minmax="min", data=data)

model = WOA.OriginalWOA(epoch=50, pop_size=20)
model.solve(problem)

print(f"Best agent: {model.g_best}")                    # Encoded solution
print(f"Best solution: {model.g_best.solution}")        # Encoded solution
print(f"Best fitness: {model.g_best.target.fitness}")
print(f"Best real scheduling: {model.problem.decode_solution(model.g_best.solution)}")      # Decoded (Real) solution

Maintenance Scheduling

In maintenance scheduling, the goal is to optimize the schedule for performing maintenance tasks on various assets or equipment. The objective is to minimize downtime and maximize the utilization of assets while considering various constraints such as resource availability, task dependencies, and time constraints.

Each element in the solution represents whether a task is assigned to an asset (1) or not (0). The schedule specifies when each task should start and which asset it is assigned to, aiming to minimize the total downtime.

By using the Mealpy, you can find an efficient maintenance schedule that minimizes downtime, maximizes asset utilization, and satisfies various constraints, ultimately optimizing the maintenance operations for improved reliability and productivity.

import numpy as np
from mealpy import BinaryVar, WOA, Problem


num_tasks = 10
num_assets = 5
task_durations = np.random.randint(1, 10, size=(num_tasks, num_assets))

data = {
    "num_tasks": num_tasks,
    "num_assets": num_assets,
    "task_durations": task_durations,
    "unassigned_penalty": -100         # Define a penalty value for no task is assigned to asset
}


class MaintenanceSchedulingProblem(Problem):
    def __init__(self, bounds=None, minmax=None, data=None, **kwargs):
        self.data = data
        super().__init__(bounds, minmax, **kwargs)

    def obj_func(self, x):
        x_decoded = self.decode_solution(x)
        x = x_decoded["task_var"]
        downtime = -np.sum(x.reshape((self.data["num_tasks"], self.data["num_assets"])) * self.data["task_durations"])
        if np.sum(x) == 0:
            downtime += self.data["unassigned_penalty"]
        return downtime


bounds = BinaryVar(n_vars=num_tasks * num_assets, name="task_var")
problem = MaintenanceSchedulingProblem(bounds=bounds, minmax="max", data=data)

model = WOA.OriginalWOA(epoch=50, pop_size=20)
model.solve(problem)

print(f"Best agent: {model.g_best}")                    # Encoded solution
print(f"Best solution: {model.g_best.solution}")        # Encoded solution
print(f"Best fitness: {model.g_best.target.fitness}")
print(f"Best real scheduling: {model.problem.decode_solution(model.g_best.solution).reshape((num_tasks, num_assets))}")      # Decoded (Real) solution

Constrained Benchmark Function

from mealpy import FloatVar, SMA
import numpy as np

## Link: https://onlinelibrary.wiley.com/doi/pdf/10.1002/9781119136507.app2
def objective_function(solution):
    def g1(x):
        return 2*x[0] + 2*x[1] + x[9] + x[10] - 10
    def g2(x):
        return 2 * x[0] + 2 * x[2] + x[9] + x[10] - 10
    def g3(x):
        return 2 * x[1] + 2 * x[2] + x[10] + x[11] - 10
    def g4(x):
        return -8*x[0] + x[9]
    def g5(x):
        return -8*x[1] + x[10]
    def g6(x):
        return -8*x[2] + x[11]
    def g7(x):
        return -2*x[3] - x[4] + x[9]
    def g8(x):
        return -2*x[5] - x[6] + x[10]
    def g9(x):
        return -2*x[7] - x[8] + x[11]

    def violate(value):
        return 0 if value <= 0 else value

    fx = 5 * np.sum(solution[:4]) - 5*np.sum(solution[:4]**2) - np.sum(solution[4:13])

    ## Increase the punishment for g1 and g4 to boost the algorithm (You can choice any constraint instead of g1 and g4)
    fx += violate(g1(solution))**2 + violate(g2(solution)) + violate(g3(solution)) + \
            2*violate(g4(solution)) + violate(g5(solution)) + violate(g6(solution))+ \
            violate(g7(solution)) + violate(g8(solution)) + violate(g9(solution))
    return fx

problem = {
    "obj_func": objective_function,
    "bounds": FloatVar(lb=[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], ub=[1, 1, 1, 1, 1, 1, 1, 1, 1, 100, 100, 100, 1]),
    "minmax": "min",
}

## Run the algorithm
optimizer = SMA.OriginalSMA(epoch=100, pop_size=50, pr=0.03)
optimizer.solve(problem)
print(f"Best solution: {optimizer.g_best.solution}, Best fitness: {optimizer.g_best.target.fitness}")

Multi-objective Benchmark Function

from mealpy import FloatVar, SMA 
import numpy as np


## Link: https://en.wikipedia.org/wiki/Test_functions_for_optimization
def objective_function(solution):

    def booth(x, y):
        return (x + 2*y - 7)**2 + (2*x + y - 5)**2

    def bukin(x, y):
        return 100 * np.sqrt(np.abs(y - 0.01 * x**2)) + 0.01 * np.abs(x + 10)

    def matyas(x, y):
        return 0.26 * (x**2 + y**2) - 0.48 * x * y

    return [booth(solution[0], solution[1]), bukin(solution[0], solution[1]), matyas(solution[0], solution[1])]


problem = {
    "obj_func": objective_function,
    "bounds": FloatVar(lb=(-10, -10), ub=(10, 10)),
    "minmax": "min",
    "obj_weights": [0.4, 0.1, 0.5]               # Define it or default value will be [1, 1, 1]
}

## Run the algorithm
optimizer = SMA.OriginalSMA(epoch=100, pop_size=50, pr=0.03)
optimizer.solve(problem)
print(f"Best solution: {optimizer.g_best.solution}, Best fitness: {optimizer.g_best.target.fitness}")

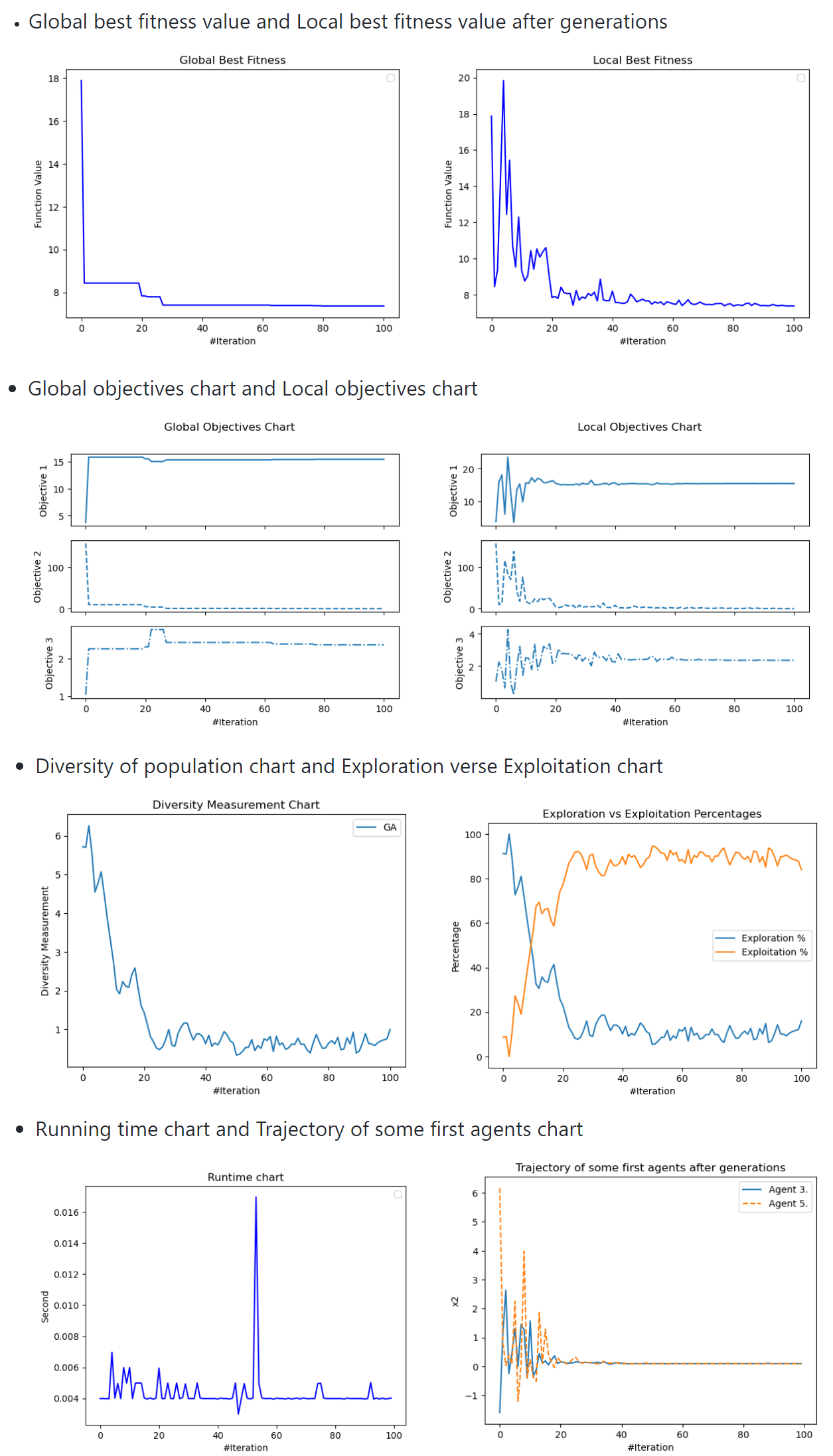
## You can access all of available figures via object "history" like this:
optimizer.history.save_global_objectives_chart(filename="hello/goc")
optimizer.history.save_local_objectives_chart(filename="hello/loc")
optimizer.history.save_global_best_fitness_chart(filename="hello/gbfc")
optimizer.history.save_local_best_fitness_chart(filename="hello/lbfc")
optimizer.history.save_runtime_chart(filename="hello/rtc")
optimizer.history.save_exploration_exploitation_chart(filename="hello/eec")
optimizer.history.save_diversity_chart(filename="hello/dc")
optimizer.history.save_trajectory_chart(list_agent_idx=[3, 5], selected_dimensions=[2], filename="hello/tc")

Custom Problem

For our custom problem, we can create a class and inherit from the Problem class, named the child class the
'Squared' class. In the initialization method of the 'Squared' class, we have to set the bounds, and minmax
of the problem (bounds: a problem's type, and minmax: a string specifying whether the problem is a 'min' or 'max' problem).

Afterwards, we have to override the abstract method obj_func(), which takes a parameter 'solution' (the solution to be evaluated) and returns the function value. The resulting code should look something like the code snippet below. 'Name' is an additional parameter we want to include in this class, and you can include any other additional parameters you need. But remember to set up all additional parameters before super() called.

from mealpy import Problem, FloatVar, BBO 
import numpy as np

# Our custom problem class
class Squared(Problem):
    def __init__(self, bounds=None, minmax="min", data=None, **kwargs):
        self.data = data 
        super().__init__(bounds, minmax, **kwargs)

    def obj_func(self, solution):
        return np.sum(solution ** 2)

    
## Now, we define an algorithm, and pass an instance of our *Squared* class as the problem argument. 
problem = Squared(bounds=FloatVar(lb=(-10., )*20, ub=(10., )*20), minmax="min", name="Squared", data="Amazing")
model = BBO.OriginalBBO(epoch=10, pop_size=50)
g_best = model.solve(problem)

## Show some attributes
print(g_best.solution)
print(g_best.target.fitness)
print(g_best.target.objectives)
print(g_best)
print(model.get_parameters())
print(model.get_name())
print(model.get_attributes()["g_best"])
print(model.problem.get_name())
print(model.problem.n_dims)
print(model.problem.bounds)
print(model.problem.lb)
print(model.problem.ub)

Tuner class (GridSearchCV/ParameterSearch, Hyper-parameter tuning)

We build a dedicated class, Tuner, that can help you tune your algorithm's parameters.

from opfunu.cec_based.cec2017 import F52017
from mealpy import FloatVar, BBO, Tuner

## You can define your own problem, here I took the F5 benchmark function in CEC-2017 as an example.
f1 = F52017(30, f_bias=0)

p1 = {
    "bounds": FloatVar(lb=f1.lb, ub=f1.ub),
    "obj_func": f1.evaluate,
    "minmax": "min",
    "name": "F5",
    "log_to": "console",
}

paras_bbo_grid = {
    "epoch": [10, 20, 30, 40],
    "pop_size": [50, 100, 150],
    "n_elites": [2, 3, 4, 5],
    "p_m": [0.01, 0.02, 0.05]
}

term = {
    "max_epoch": 200,
    "max_time": 20,
    "max_fe": 10000
}

if __name__ == "__main__":
    model = BBO.OriginalBBO()
    tuner = Tuner(model, paras_bbo_grid)
    tuner.execute(problem=p1, termination=term, n_trials=5, n_jobs=4, mode="thread", n_workers=4, verbose=True)
    ## Solve this problem 5 times (n_trials) using 5 processes (n_jobs), each process will handle 1 trial. 
    ## The mode to run the solver is thread (mode), distributed to 4 threads 

    print(tuner.best_row)
    print(tuner.best_score)
    print(tuner.best_params)
    print(type(tuner.best_params))
    print(tuner.best_algorithm)
    
    ## Save results to csv file 
    tuner.export_results(save_path="history", file_name="tuning_best_fit.csv")
    tuner.export_figures()
    
    ## Re-solve the best model on your problem 
    g_best = tuner.resolve(mode="thread", n_workers=4, termination=term)
    print(g_best.solution, g_best.target.fitness)
    print(tuner.algorithm.problem.get_name())
    print(tuner.best_algorithm.get_name())

Multitask class (Multitask solver)

We also build a dedicated class, Multitask, that can help you run several scenarios. For example:

1. Run 1 algorithm with 1 problem, and multiple trials
2. Run 1 algorithm with multiple problems, and multiple trials
3. Run multiple algorithms with 1 problem, and multiple trials
4. Run multiple algorithms with multiple problems, and multiple trials

#### Using multiple algorithm to solve multiple problems with multiple trials

## Import libraries
from opfunu.cec_based.cec2017 import F52017, F102017, F292017
from mealpy import FloatVar
from mealpy import BBO, DE
from mealpy import Multitask

## Define your own problems
f1 = F52017(30, f_bias=0)
f2 = F102017(30, f_bias=0)
f3 = F292017(30, f_bias=0)

p1 = {
    "bounds": FloatVar(lb=f1.lb, ub=f1.ub),
    "obj_func": f1.evaluate,
    "minmax": "min",
    "name": "F5",
    "log_to": "console",
}

p2 = {
    "bounds": FloatVar(lb=f2.lb, ub=f2.ub),
    "obj_func": f2.evaluate,
    "minmax": "min",
    "name": "F10",
    "log_to": "console",
}

p3 = {
    "bounds": FloatVar(lb=f3.lb, ub=f3.ub),
    "obj_func": f3.evaluate,
    "minmax": "min",
    "name": "F29",
    "log_to": "console",
}

## Define models
model1 = BBO.DevBBO(epoch=10000, pop_size=50)
model2 = BBO.OriginalBBO(epoch=10000, pop_size=50)
model3 = DE.OriginalDE(epoch=10000, pop_size=50)
model4 = DE.SAP_DE(epoch=10000, pop_size=50)

## Define termination if needed
term = {
    "max_fe": 3000
}

## Define and run Multitask
if __name__ == "__main__":
    multitask = Multitask(algorithms=(model1, model2, model3, model4), problems=(p1, p2, p3), terminations=(term, ), modes=("thread", ), n_workers=4)
    # default modes = "single", default termination = epoch (as defined in problem dictionary)
    multitask.execute(n_trials=5, n_jobs=None, save_path="history", save_as="csv", save_convergence=True, verbose=False)
    # multitask.execute(n_trials=5, save_path="history", save_as="csv", save_convergence=True, verbose=False)
    
    ## Check the directory: history/, you will see list of .csv result files

For more usage examples please look at examples folder.

More advanced examples can also be found in the Mealpy-examples repository.

Get Visualize Figures

• Tutorials

All Optimizers

import numpy as np
from opfunu.cec_based.cec2017 import F292017

from mealpy import BBO, PSO, GA, ALO, AO, ARO, AVOA, BA, BBOA, BMO, EOA, IWO
from mealpy import FloatVar
from mealpy import GJO, FOX, FOA, FFO, FFA, FA, ESOA, EHO, DO, DMOA, CSO, CSA, CoatiOA, COA, BSA
from mealpy import HCO, ICA, LCO, WarSO, TOA, TLO, SSDO, SPBO, SARO, QSA, ArchOA, ASO, CDO, EFO, EO, EVO, FLA
from mealpy import HGSO, MVO, NRO, RIME, SA, WDO, TWO, ABC, ACOR, AGTO, BeesA, BES, BFO, ZOA, WOA, WaOA, TSO
from mealpy import PFA, OOA, NGO, NMRA, MSA, MRFO, MPA, MGO, MFO, JA, HHO, HGS, HBA, GWO, GTO, GOA
from mealpy import Problem
from mealpy import SBO, SMA, SOA, SOS, TPO, TSA, VCS, WHO, AOA, CEM, CGO, CircleSA, GBO, HC, INFO, PSS, RUN, SCA
from mealpy import SHIO, TS, HS, AEO, GCO, WCA, CRO, DE, EP, ES, FPA, MA, SHADE, BRO, BSO, CA, CHIO, FBIO, GSKA, HBO
from mealpy import TDO, STO, SSpiderO, SSpiderA, SSO, SSA, SRSR, SLO, SHO, SFO, ServalOA, SeaHO, SCSO, POA
from mealpy import (StringVar, FloatVar, BoolVar, PermutationVar, MixedSetVar, IntegerVar, BinaryVar,
                    TransferBinaryVar, TransferBoolVar)
from mealpy import Tuner, Multitask, Problem, Optimizer, Termination, ParameterGrid
from mealpy import get_all_optimizers, get_optimizer_by_name



if __name__ == "__main__":
    model = BBO.OriginalBBO(epoch=10, pop_size=30, p_m=0.01, n_elites=2)
    model = PSO.OriginalPSO(epoch=100, pop_size=50, c1=2.05, c2=20.5, w=0.4)
    model = PSO.LDW_PSO(epoch=100, pop_size=50, c1=2.05, c2=20.5, w_min=0.4, w_max=0.9)
    model = PSO.AIW_PSO(epoch=100, pop_size=50, c1=2.05, c2=20.5, alpha=0.4)
    model = PSO.P_PSO(epoch=100, pop_size=50)
    model = PSO.HPSO_TVAC(epoch=100, pop_size=50, ci=0.5, cf=0.1)
    model = PSO.C_PSO(epoch=100, pop_size=50, c1=2.05, c2=2.05, w_min=0.4, w_max=0.9)
    model = PSO.CL_PSO(epoch=100, pop_size=50, c_local=1.2, w_min=0.4, w_max=0.9, max_flag=7)
    model = GA.BaseGA(epoch=100, pop_size=50, pc=0.9, pm=0.05, selection="tournament", k_way=0.4, crossover="multi_points", mutation="swap")
    model = GA.SingleGA(epoch=100, pop_size=50, pc=0.9, pm=0.8, selection="tournament", k_way=0.4, crossover="multi_points", mutation="swap")
    model = GA.MultiGA(epoch=100, pop_size=50, pc=0.9, pm=0.8, selection="tournament", k_way=0.4, crossover="multi_points", mutation="swap")
    model = GA.EliteSingleGA(epoch=100, pop_size=50, pc=0.95, pm=0.8, selection="roulette", crossover="uniform", mutation="swap", k_way=0.2, elite_best=0.1,
                             elite_worst=0.3, strategy=0)
    model = GA.EliteMultiGA(epoch=100, pop_size=50, pc=0.95, pm=0.8, selection="roulette", crossover="uniform", mutation="swap", k_way=0.2, elite_best=0.1,
                            elite_worst=0.3, strategy=0)
    model = ABC.OriginalABC(epoch=1000, pop_size=50, n_limits=50)
    model = ACOR.OriginalACOR(epoch=1000, pop_size=50, sample_count=25, intent_factor=0.5, zeta=1.0)
    model = AGTO.OriginalAGTO(epoch=1000, pop_size=50, p1=0.03, p2=0.8, beta=3.0)
    model = AGTO.MGTO(epoch=1000, pop_size=50, pp=0.03)
    model = ALO.OriginalALO(epoch=100, pop_size=50)
    model = ALO.DevALO(epoch=100, pop_size=50)
    model = AO.OriginalAO(epoch=100, pop_size=50)
    model = ARO.OriginalARO(epoch=100, pop_size=50)
    model = ARO.LARO(epoch=100, pop_size=50)
    model = ARO.IARO(epoch=100, pop_size=50)
    model = AVOA.OriginalAVOA(epoch=100, pop_size=50, p1=0.6, p2=0.4, p3=0.6, alpha=0.8, gama=2.5)
    model = BA.OriginalBA(epoch=100, pop_size=50, loudness=0.8, pulse_rate=0.95, pf_min=0.1, pf_max=10.0)
    model = BA.AdaptiveBA(epoch=100, pop_size=50, loudness_min=1.0, loudness_max=2.0, pr_min=-2.5, pr_max=0.85, pf_min=0.1, pf_max=10.)
    model = BA.DevBA(epoch=100, pop_size=50, pulse_rate=0.95, pf_min=0., pf_max=10.)
    model = BBOA.OriginalBBOA(epoch=100, pop_size=50)
    model = BMO.OriginalBMO(epoch=100, pop_size=50, pl=4)
    model = EOA.OriginalEOA(epoch=100, pop_size=50, p_c=0.9, p_m=0.01, n_best=2, alpha=0.98, beta=0.9, gama=0.9)
    model = IWO.OriginalIWO(epoch=100, pop_size=50, seed_min=3, seed_max=9, exponent=3, sigma_start=0.6, sigma_end=0.01)
    model = SBO.DevSBO(epoch=100, pop_size=50, alpha=0.9, p_m=0.05, psw=0.02)
    model = SBO.OriginalSBO(epoch=100, pop_size=50, alpha=0.9, p_m=0.05, psw=0.02)
    model = SMA.OriginalSMA(epoch=100, pop_size=50, p_t=0.03)
    model = SMA.DevSMA(epoch=100, pop_size=50, p_t=0.03)
    model = SOA.OriginalSOA(epoch=100, pop_size=50, fc=2)
    model = SOA.DevSOA(epoch=100, pop_size=50, fc=2)
    model = SOS.OriginalSOS(epoch=100, pop_size=50)
    model = TPO.DevTPO(epoch=100, pop_size=50, alpha=0.3, beta=50., theta=0.9)
    model = TSA.OriginalTSA(epoch=100, pop_size=50)
    model = VCS.OriginalVCS(epoch=100, pop_size=50, lamda=0.5, sigma=0.3)
    model = VCS.DevVCS(epoch=100, pop_size=50, lamda=0.5, sigma=0.3)
    model = WHO.OriginalWHO(epoch=100, pop_size=50, n_explore_step=3, n_exploit_step=3, eta=0.15, p_hi=0.9, local_alpha=0.9, local_beta=0.3, global_alpha=0.2,
                            global_beta=0.8, delta_w=2.0, delta_c=2.0)
    model = AOA.OriginalAOA(epoch=100, pop_size=50, alpha=5, miu=0.5, moa_min=0.2, moa_max=0.9)
    model = CEM.OriginalCEM(epoch=100, pop_size=50, n_best=20, alpha=0.7)
    model = CGO.OriginalCGO(epoch=100, pop_size=50)
    model = CircleSA.OriginalCircleSA(epoch=100, pop_size=50, c_factor=0.8)
    model = GBO.OriginalGBO(epoch=100, pop_size=50, pr=0.5, beta_min=0.2, beta_max=1.2)
    model = HC.OriginalHC(epoch=100, pop_size=50, neighbour_size=50)
    model = HC.SwarmHC(epoch=100, pop_size=50, neighbour_size=10)
    model = INFO.OriginalINFO(epoch=100, pop_size=50)
    model = PSS.OriginalPSS(epoch=100, pop_size=50, acceptance_rate=0.8, sampling_method="LHS")
    model = RUN.OriginalRUN(epoch=100, pop_size=50)
    model = SCA.OriginalSCA(epoch=100, pop_size=50)
    model = SCA.DevSCA(epoch=100, pop_size=50)
    model = SCA.QleSCA(epoch=100, pop_size=50, alpha=0.1, gama=0.9)
    model = SHIO.OriginalSHIO(epoch=100, pop_size=50)
    model = TS.OriginalTS(epoch=100, pop_size=50, tabu_size=5, neighbour_size=20, perturbation_scale=0.05)
    model = HS.OriginalHS(epoch=100, pop_size=50, c_r=0.95, pa_r=0.05)
    model = HS.DevHS(epoch=100, pop_size=50, c_r=0.95, pa_r=0.05)
    model = AEO.OriginalAEO(epoch=100, pop_size=50)
    model = AEO.EnhancedAEO(epoch=100, pop_size=50)
    model = AEO.ModifiedAEO(epoch=100, pop_size=50)
    model = AEO.ImprovedAEO(epoch=100, pop_size=50)
    model = AEO.AugmentedAEO(epoch=100, pop_size=50)
    model = GCO.OriginalGCO(epoch=100, pop_size=50, cr=0.7, wf=1.25)
    model = GCO.DevGCO(epoch=100, pop_size=50, cr=0.7, wf=1.25)
    model = WCA.OriginalWCA(epoch=100, pop_size=50, nsr=4, wc=2.0, dmax=1e-6)
    model = CRO.OriginalCRO(epoch=100, pop_size=50, po=0.4, Fb=0.9, Fa=0.1, Fd=0.1, Pd=0.5, GCR=0.1, gamma_min=0.02, gamma_max=0.2, n_trials=5)
    model = CRO.OCRO(epoch=100, pop_size=50, po=0.4, Fb=0.9, Fa=0.1, Fd=0.1, Pd=0.5, GCR=0.1, gamma_min=0.02, gamma_max=0.2, n_trials=5, restart_count=50)
    model = DE.OriginalDE(epoch=100, pop_size=50, wf=0.7, cr=0.9, strategy=0)
    model = DE.JADE(epoch=100, pop_size=50, miu_f=0.5, miu_cr=0.5, pt=0.1, ap=0.1)
    model = DE.SADE(epoch=100, pop_size=50)
    model = DE.SAP_DE(epoch=100, pop_size=50, branch="ABS")
    model = EP.OriginalEP(epoch=100, pop_size=50, bout_size=0.05)
    model = EP.LevyEP(epoch=100, pop_size=50, bout_size=0.05)
    model = ES.OriginalES(epoch=100, pop_size=50, lamda=0.75)
    model = ES.LevyES(epoch=100, pop_size=50, lamda=0.75)
    model = ES.CMA_ES(epoch=100, pop_size=50)
    model = ES.Simple_CMA_ES(epoch=100, pop_size=50)
    model = FPA.OriginalFPA(epoch=100, pop_size=50, p_s=0.8, levy_multiplier=0.2)
    model = MA.OriginalMA(epoch=100, pop_size=50, pc=0.85, pm=0.15, p_local=0.5, max_local_gens=10, bits_per_param=4)
    model = SHADE.OriginalSHADE(epoch=100, pop_size=50, miu_f=0.5, miu_cr=0.5)
    model = SHADE.L_SHADE(epoch=100, pop_size=50, miu_f=0.5, miu_cr=0.5)
    model = BRO.OriginalBRO(epoch=100, pop_size=50, threshold=3)
    model = BRO.DevBRO(epoch=100, pop_size=50, threshold=3)
    model = BSO.OriginalBSO(epoch=100, pop_size=50, m_clusters=5, p1=0.2, p2=0.8, p3=0.4, p4=0.5, slope=20)
    model = BSO.ImprovedBSO(epoch=100, pop_size=50, m_clusters=5, p1=0.25, p2=0.5, p3=0.75, p4=0.6)
    model = CA.OriginalCA(epoch=100, pop_size=50, accepted_rate=0.15)
    model = CHIO.OriginalCHIO(epoch=100, pop_size=50, brr=0.15, max_age=10)
    model = CHIO.DevCHIO(epoch=100, pop_size=50, brr=0.15, max_age=10)
    model = FBIO.OriginalFBIO(epoch=100, pop_size=50)
    model = FBIO.DevFBIO(epoch=100, pop_size=50)
    model = GSKA.OriginalGSKA(epoch=100, pop_size=50, pb=0.1, kf=0.5, kr=0.9, kg=5)
    model = GSKA.DevGSKA(epoch=100, pop_size=50, pb=0.1, kr=0.9)
    model = HBO.OriginalHBO(epoch=100, pop_size=50, degree=3)
    model = HCO.OriginalHCO(epoch=100, pop_size=50, wfp=0.65, wfv=0.05, c1=1.4, c2=1.4)
    model = ICA.OriginalICA(epoch=100, pop_size=50, empire_count=5, assimilation_coeff=1.5, revolution_prob=0.05, revolution_rate=0.1, revolution_step_size=0.1,
                            zeta=0.1)
    model = LCO.OriginalLCO(epoch=100, pop_size=50, r1=2.35)
    model = LCO.ImprovedLCO(epoch=100, pop_size=50)
    model = LCO.DevLCO(epoch=100, pop_size=50, r1=2.35)
    model = WarSO.OriginalWarSO(epoch=100, pop_size=50, rr=0.1)
    model = TOA.OriginalTOA(epoch=100, pop_size=50)
    model = TLO.OriginalTLO(epoch=100, pop_size=50)
    model = TLO.ImprovedTLO(epoch=100, pop_size=50, n_teachers=5)
    model = TLO.DevTLO(epoch=100, pop_size=50)
    model = SSDO.OriginalSSDO(epoch=100, pop_size=50)
    model = SPBO.OriginalSPBO(epoch=100, pop_size=50)
    model = SPBO.DevSPBO(epoch=100, pop_size=50)
    model = SARO.OriginalSARO(epoch=100, pop_size=50, se=0.5, mu=50)
    model = SARO.DevSARO(epoch=100, pop_size=50, se=0.5, mu=50)
    model = QSA.OriginalQSA(epoch=100, pop_size=50)
    model = QSA.DevQSA(epoch=100, pop_size=50)
    model = QSA.OppoQSA(epoch=100, pop_size=50)
    model = QSA.LevyQSA(epoch=100, pop_size=50)
    model = QSA.ImprovedQSA(epoch=100, pop_size=50)
    model = ArchOA.OriginalArchOA(epoch=100, pop_size=50, c1=2, c2=5, c3=2, c4=0.5, acc_max=0.9, acc_min=0.1)
    model = ASO.OriginalASO(epoch=100, pop_size=50, alpha=50, beta=0.2)
    model = CDO.OriginalCDO(epoch=100, pop_size=50)
    model = EFO.OriginalEFO(epoch=100, pop_size=50, r_rate=0.3, ps_rate=0.85, p_field=0.1, n_field=0.45)
    model = EFO.DevEFO(epoch=100, pop_size=50, r_rate=0.3, ps_rate=0.85, p_field=0.1, n_field=0.45)
    model = EO.OriginalEO(epoch=100, pop_size=50)
    model = EO.AdaptiveEO(epoch=100, pop_size=50)
    model = EO.ModifiedEO(epoch=100, pop_size=50)
    model = EVO.OriginalEVO(epoch=100, pop_size=50)
    model = FLA.OriginalFLA(epoch=100, pop_size=50, C1=0.5, C2=2.0, C3=0.1, C4=0.2, C5=2.0, DD=0.01)
    model = HGSO.OriginalHGSO(epoch=100, pop_size=50, n_clusters=3)
    model = MVO.OriginalMVO(epoch=100, pop_size=50, wep_min=0.2, wep_max=1.0)
    model = MVO.DevMVO(epoch=100, pop_size=50, wep_min=0.2, wep_max=1.0)
    model = NRO.OriginalNRO(epoch=100, pop_size=50)
    model = RIME.OriginalRIME(epoch=100, pop_size=50, sr=5.0)
    model = SA.OriginalSA(epoch=100, pop_size=50, temp_init=100, step_size=0.1)
    model = SA.GaussianSA(epoch=100, pop_size=50, temp_init=100, cooling_rate=0.99, scale=0.1)
    model = SA.SwarmSA(epoch=100, pop_size=50, max_sub_iter=5, t0=1000, t1=1, move_count=5, mutation_rate=0.1, mutation_step_size=0.1,
                       mutation_step_size_damp=0.99)
    model = WDO.OriginalWDO(epoch=100, pop_size=50, RT=3, g_c=0.2, alp=0.4, c_e=0.4, max_v=0.3)
    model = TWO.OriginalTWO(epoch=100, pop_size=50)
    model = TWO.EnhancedTWO(epoch=100, pop_size=50)
    model = TWO.OppoTWO(epoch=100, pop_size=50)
    model = TWO.LevyTWO(epoch=100, pop_size=50)
    model = ABC.OriginalABC(epoch=100, pop_size=50, n_limits=50)
    model = ACOR.OriginalACOR(epoch=100, pop_size=50, sample_count=25, intent_factor=0.5, zeta=1.0)
    model = AGTO.OriginalAGTO(epoch=100, pop_size=50, p1=0.03, p2=0.8, beta=3.0)
    model = AGTO.MGTO(epoch=100, pop_size=50, pp=0.03)
    model = BeesA.OriginalBeesA(epoch=100, pop_size=50, selected_site_ratio=0.5, elite_site_ratio=0.4, selected_site_bee_ratio=0.1, elite_site_bee_ratio=2.0,
                                dance_radius=0.1, dance_reduction=0.99)
    model = BeesA.CleverBookBeesA(epoch=100, pop_size=50, n_elites=16, n_others=4, patch_size=5.0, patch_reduction=0.985, n_sites=3, n_elite_sites=1)
    model = BeesA.ProbBeesA(epoch=100, pop_size=50, recruited_bee_ratio=0.1, dance_radius=0.1, dance_reduction=0.99)
    model = BES.OriginalBES(epoch=100, pop_size=50, a_factor=10, R_factor=1.5, alpha=2.0, c1=2.0, c2=2.0)
    model = BFO.OriginalBFO(epoch=100, pop_size=50, Ci=0.01, Ped=0.25, Nc=5, Ns=4, d_attract=0.1, w_attract=0.2, h_repels=0.1, w_repels=10)
    model = BFO.ABFO(epoch=100, pop_size=50, C_s=0.1, C_e=0.001, Ped=0.01, Ns=4, N_adapt=2, N_split=40)
    model = ZOA.OriginalZOA(epoch=100, pop_size=50)
    model = WOA.OriginalWOA(epoch=100, pop_size=50)
    model = WOA.HI_WOA(epoch=100, pop_size=50, feedback_max=10)
    model = WaOA.OriginalWaOA(epoch=100, pop_size=50)
    model = TSO.OriginalTSO(epoch=100, pop_size=50)
    model = TDO.OriginalTDO(epoch=100, pop_size=50)
    model = STO.OriginalSTO(epoch=100, pop_size=50)
    model = SSpiderO.OriginalSSpiderO(epoch=100, pop_size=50, fp_min=0.65, fp_max=0.9)
    model = SSpiderA.OriginalSSpiderA(epoch=100, pop_size=50, r_a=1.0, p_c=0.7, p_m=0.1)
    model = SSO.OriginalSSO(epoch=100, pop_size=50)
    model = SSA.OriginalSSA(epoch=100, pop_size=50, ST=0.8, PD=0.2, SD=0.1)
    model = SSA.DevSSA(epoch=100, pop_size=50, ST=0.8, PD=0.2, SD=0.1)
    model = SRSR.OriginalSRSR(epoch=100, pop_size=50)
    model = SLO.OriginalSLO(epoch=100, pop_size=50)
    model = SLO.ModifiedSLO(epoch=100, pop_size=50)
    model = SLO.ImprovedSLO(epoch=100, pop_size=50, c1=1.2, c2=1.5)
    model = SHO.OriginalSHO(epoch=100, pop_size=50, h_factor=5.0, n_trials=10)
    model = SFO.OriginalSFO(epoch=100, pop_size=50, pp=0.1, AP=4.0, epsilon=0.0001)
    model = SFO.ImprovedSFO(epoch=100, pop_size=50, pp=0.1)
    model = ServalOA.OriginalServalOA(epoch=100, pop_size=50)
    model = SeaHO.OriginalSeaHO(epoch=100, pop_size=50)
    model = SCSO.OriginalSCSO(epoch=100, pop_size=50)
    model = POA.OriginalPOA(epoch=100, pop_size=50)
    model = PFA.OriginalPFA(epoch=100, pop_size=50)
    model = OOA.OriginalOOA(epoch=100, pop_size=50)
    model = NGO.OriginalNGO(epoch=100, pop_size=50)
    model = NMRA.OriginalNMRA(epoch=100, pop_size=50, pb=0.75)
    model = NMRA.ImprovedNMRA(epoch=100, pop_size=50, pb=0.75, pm=0.01)
    model = MSA.OriginalMSA(epoch=100, pop_size=50, n_best=5, partition=0.5, max_step_size=1.0)
    model = MRFO.OriginalMRFO(epoch=100, pop_size=50, somersault_range=2.0)
    model = MRFO.WMQIMRFO(epoch=100, pop_size=50, somersault_range=2.0, pm=0.5)
    model = MPA.OriginalMPA(epoch=100, pop_size=50)
    model = MGO.OriginalMGO(epoch=100, pop_size=50)
    model = MFO.OriginalMFO(epoch=100, pop_size=50)
    model = JA.OriginalJA(epoch=100, pop_size=50)
    model = JA.LevyJA(epoch=100, pop_size=50)
    model = JA.DevJA(epoch=100, pop_size=50)
    model = HHO.OriginalHHO(epoch=100, pop_size=50)
    model = HGS.OriginalHGS(epoch=100, pop_size=50, PUP=0.08, LH=10000)
    model = HBA.OriginalHBA(epoch=100, pop_size=50)
    model = GWO.OriginalGWO(epoch=100, pop_size=50)
    model = GWO.GWO_WOA(epoch=100, pop_size=50)
    model = GWO.RW_GWO(epoch=100, pop_size=50)
    model = GTO.OriginalGTO(epoch=100, pop_size=50, A=0.4, H=2.0)
    model = GTO.Matlab101GTO(epoch=100, pop_size=50)
    model = GTO.Matlab102GTO(epoch=100, pop_size=50)
    model = GOA.OriginalGOA(epoch=100, pop_size=50, c_min=0.00004, c_max=1.0)
    model = GJO.OriginalGJO(epoch=100, pop_size=50)
    model = FOX.OriginalFOX(epoch=100, pop_size=50, c1=0.18, c2=0.82)
    model = FOA.OriginalFOA(epoch=100, pop_size=50)
    model = FOA.WhaleFOA(epoch=100, pop_size=50)
    model = FOA.DevFOA(epoch=100, pop_size=50)
    model = FFO.OriginalFFO(epoch=100, pop_size=50)
    model = FFA.OriginalFFA(epoch=100, pop_size=50, gamma=0.001, beta_base=2, alpha=0.2, alpha_damp=0.99, delta=0.05, exponent=2)
    model = FA.OriginalFA(epoch=100, pop_size=50, max_sparks=50, p_a=0.04, p_b=0.8, max_ea=40, m_sparks=50)
    model = ESOA.OriginalESOA(epoch=100, pop_size=50)
    model = EHO.OriginalEHO(epoch=100, pop_size=50, alpha=0.5, beta=0.5, n_clans=5)
    model = DO.OriginalDO(epoch=100, pop_size=50)
    model = DMOA.OriginalDMOA(epoch=100, pop_size=50, n_baby_sitter=3, peep=2)
    model = DMOA.DevDMOA(epoch=100, pop_size=50, peep=2)
    model = CSO.OriginalCSO(epoch=100, pop_size=50, mixture_ratio=0.15, smp=5, spc=False, cdc=0.8, srd=0.15, c1=0.4, w_min=0.4, w_max=0.9)
    model = CSA.OriginalCSA(epoch=100, pop_size=50, p_a=0.3)
    model = CoatiOA.OriginalCoatiOA(epoch=100, pop_size=50)
    model = COA.OriginalCOA(epoch=100, pop_size=50, n_coyotes=5)
    model = BSA.OriginalBSA(epoch=100, pop_size=50, ff=10, pff=0.8, c1=1.5, c2=1.5, a1=1.0, a2=1.0, fc=0.5)

Mealpy Application

Mealpy + Neural Network (Replace the Gradient Descent Optimizer)

• Time-series Problem:
  • Traditional MLP code: Link
  • Hybrid code (Mealpy + MLP): Link
• Classification Problem:
  • Traditional MLP code: Link
  • Hybrid code (Mealpy + MLP): Link

Mealpy + Neural Network (Optimize Neural Network Hyper-parameter)

Code: Link

Other Applications

• Solving Knapsack Problem (Discrete problems): Link

• Solving Product Planning Problem (Discrete problems): Link

• Optimize SVM (SVC) model: Link

• Optimize Linear Regression Model: Link

• Travelling Salesman Problem: https://github.com/thieu1995/MHA-TSP

• Feature selection problem: https://github.com/thieu1995/MHA-FS

Get Visualize Figures

• Tutorials

Tutorial Videos

All tutorial videos: Link

All code examples: Link

All visualization examples: Link

Documents

Official Channels (questions, problems)

• Official source code repo: https://github.com/thieu1995/mealpy

• Official document: https://mealpy.readthedocs.io/

• Download releases: https://pypi.org/project/mealpy/

• Issue tracker: https://github.com/thieu1995/mealpy/issues

• Notable changes log: https://github.com/thieu1995/mealpy/blob/master/ChangeLog.md

• Examples with different meapy version: https://github.com/thieu1995/mealpy/blob/master/EXAMPLES.md

• Official chat/support group: https://t.me/+fRVCJGuGJg1mNDg1

• This project also related to our another projects which are optimization and machine learning. Check it here:

  • https://github.com/thieu1995/opfunu
  • https://github.com/thieu1995/metaheuristics
  • https://github.com/mafese
  • https://github.com/permetrics
  • https://github.com/pfevaluator
  • https://github.com/MetaCluster
  • https://github.com/enoppy
  • https://github.com/aiir-team

My Comments

• Meta-heuristic Categories: (Based on this article: link)

  • Evolutionary-based: Idea from Darwin's law of natural selection, evolutionary computing
  • Swarm-based: Idea from movement, interaction of birds, organization of social ...
  • Physics-based: Idea from physics law such as Newton's law of universal gravitation, black hole, multiverse
  • Human-based: Idea from human interaction such as queuing search, teaching learning, ...
  • Biology-based: Idea from biology creature (or microorganism),...
  • System-based: Idea from eco-system, immune-system, network-system, ...
  • Math-based: Idea from mathematical form or mathematical law such as sin-cosin
  • Music-based: Idea from music instrument

• Difficulty - Difficulty Level (Personal Opinion): Objective observation from author. Depend on the number of parameters, number of equations, the original ideas, time spend for coding, source lines of code (SLOC).

  • Easy: A few paras, few equations, SLOC very short
  • Medium: more equations than Easy level, SLOC longer than Easy level
  • Hard: Lots of equations, SLOC longer than Medium level, the paper hard to read.
  • Hard* - Very hard: Lots of equations, SLOC too long, the paper is very hard to read.

** For newbie, we recommend to read the paper of algorithms which difficulty is "easy" or "medium" difficulty level.

Group	Name	Module	Class	Year	Paras	Difficulty
Evolutionary	Evolutionary Programming	EP	OriginalEP	1964	3	easy
Evolutionary	*	*	LevyEP	*	3	easy
Evolutionary	Evolution Strategies	ES	OriginalES	1971	3	easy
Evolutionary	*	*	LevyES	*	3	easy
Evolutionary	*	*	CMA_ES	2003	2	hard
Evolutionary	*	*	Simple_CMA_ES	2023	2	medium
Evolutionary	Memetic Algorithm	MA	OriginalMA	1989	7	easy
Evolutionary	Genetic Algorithm	GA	BaseGA	1992	4	easy
Evolutionary	*	*	SingleGA	*	7	easy
Evolutionary	*	*	MultiGA	*	7	easy
Evolutionary	*	*	EliteSingleGA	*	10	easy
Evolutionary	*	*	EliteMultiGA	*	10	easy
Evolutionary	Differential Evolution	DE	BaseDE	1997	5	easy
Evolutionary	*	*	JADE	2009	6	medium
Evolutionary	*	*	SADE	2005	2	medium
Evolutionary	*	*	SAP_DE	2006	3	medium
Evolutionary	Success-History Adaptation Differential Evolution	SHADE	OriginalSHADE	2013	4	medium
Evolutionary	*	*	L_SHADE	2014	4	medium
Evolutionary	Flower Pollination Algorithm	FPA	OriginalFPA	2014	4	medium
Evolutionary	Coral Reefs Optimization	CRO	OriginalCRO	2014	11	medium
Evolutionary	*	*	OCRO	2019	12	medium
***	***	***	***	***	***	***
Swarm	Particle Swarm Optimization	PSO	OriginalPSO	1995	6	easy
Swarm	*	*	PPSO	2019	2	medium
Swarm	*	*	HPSO_TVAC	2017	4	medium
Swarm	*	*	C_PSO	2015	6	medium
Swarm	*	*	CL_PSO	2006	6	medium
Swarm	Bacterial Foraging Optimization	BFO	OriginalBFO	2002	10	hard
Swarm	*	*	ABFO	2019	8	medium
Swarm	Bees Algorithm	BeesA	OriginalBeesA	2005	8	medium
Swarm	*	*	ProbBeesA	2015	5	medium
Swarm	*	*	CleverBookBeesA	2006	8	medium
Swarm	Cat Swarm Optimization	CSO	OriginalCSO	2006	11	hard
Swarm	Artificial Bee Colony	ABC	OriginalABC	2007	8	medium
Swarm	Ant Colony Optimization	ACOR	OriginalACOR	2008	5	easy
Swarm	Cuckoo Search Algorithm	CSA	OriginalCSA	2009	3	medium
Swarm	Firefly Algorithm	FFA	OriginalFFA	2009	8	easy
Swarm	Fireworks Algorithm	FA	OriginalFA	2010	7	medium
Swarm	Bat Algorithm	BA	OriginalBA	2010	6	medium
Swarm	*	*	AdaptiveBA	2010	8	medium
Swarm	*	*	ModifiedBA	*	5	medium
Swarm	Fruit-fly Optimization Algorithm	FOA	OriginalFOA	2012	2	easy
Swarm	*	*	BaseFOA	*	2	easy
Swarm	*	*	WhaleFOA	2020	2	medium
Swarm	Social Spider Optimization	SSpiderO	OriginalSSpiderO	2018	4	hard*
Swarm	Grey Wolf Optimizer	GWO	OriginalGWO	2014	2	easy
Swarm	*	*	RW_GWO	2019	2	easy
Swarm	Social Spider Algorithm	SSpiderA	OriginalSSpiderA	2015	5	medium
Swarm	Ant Lion Optimizer	ALO	OriginalALO	2015	2	easy
Swarm	*	*	BaseALO	*	2	easy
Swarm	Moth Flame Optimization	MFO	OriginalMFO	2015	2	easy
Swarm	*	*	BaseMFO	*	2	easy
Swarm	Elephant Herding Optimization	EHO	OriginalEHO	2015	5	easy
Swarm	Jaya Algorithm	JA	OriginalJA	2016	2	easy
Swarm	*	*	BaseJA	*	2	easy
Swarm	*	*	LevyJA	2021	2	easy
Swarm	Whale Optimization Algorithm	WOA	OriginalWOA	2016	2	medium
Swarm	*	*	HI_WOA	2019	3	medium
Swarm	Dragonfly Optimization	DO	OriginalDO	2016	2	medium
Swarm	Bird Swarm Algorithm	BSA	OriginalBSA	2016	9	medium
Swarm	Spotted Hyena Optimizer	SHO	OriginalSHO	2017	4	medium
Swarm	Salp Swarm Optimization	SSO	OriginalSSO	2017	2	easy
Swarm	Swarm Robotics Search And Rescue	SRSR	OriginalSRSR	2017	2	hard*
Swarm	Grasshopper Optimisation Algorithm	GOA	OriginalGOA	2017	4	easy
Swarm	Coyote Optimization Algorithm	COA	OriginalCOA	2018	3	medium
Swarm	Moth Search Algorithm	MSA	OriginalMSA	2018	5	easy
Swarm	Sea Lion Optimization	SLO	OriginalSLO	2019	2	medium
Swarm	*	*	ModifiedSLO	*	2	medium
Swarm	*	*	ImprovedSLO	2022	4	medium
Swarm	Nake Mole*Rat Algorithm	NMRA	OriginalNMRA	2019	3	easy
Swarm	*	*	ImprovedNMRA	*	4	medium
Swarm	Pathfinder Algorithm	PFA	OriginalPFA	2019	2	medium
Swarm	Sailfish Optimizer	SFO	OriginalSFO	2019	5	easy
Swarm	*	*	ImprovedSFO	*	3	medium
Swarm	Harris Hawks Optimization	HHO	OriginalHHO	2019	2	medium
Swarm	Manta Ray Foraging Optimization	MRFO	OriginalMRFO	2020	3	medium
Swarm	Bald Eagle Search	BES	OriginalBES	2020	7	easy
Swarm	Sparrow Search Algorithm	SSA	OriginalSSA	2020	5	medium
Swarm	*	*	BaseSSA	*	5	medium
Swarm	Hunger Games Search	HGS	OriginalHGS	2021	4	medium
Swarm	Aquila Optimizer	AO	OriginalAO	2021	2	easy
Swarm	Hybrid Grey Wolf * Whale Optimization Algorithm	GWO	GWO_WOA	2022	2	easy
Swarm	Marine Predators Algorithm	MPA	OriginalMPA	2020	2	medium
Swarm	Honey Badger Algorithm	HBA	OriginalHBA	2022	2	easy
Swarm	Sand Cat Swarm Optimization	SCSO	OriginalSCSO	2022	2	easy
Swarm	Tuna Swarm Optimization	TSO	OriginalTSO	2021	2	medium
Swarm	African Vultures Optimization Algorithm	AVOA	OriginalAVOA	2022	7	medium
Swarm	Artificial Gorilla Troops Optimization	AGTO	OriginalAGTO	2021	5	medium
Swarm	*	*	MGTO	2023	3	medium
Swarm	Artificial Rabbits Optimization	ARO	OriginalARO	2022	2	easy
Swarm	*	*	LARO	2022	2	easy
Swarm	*	*	IARO	2022	2	easy
Swarm	Egret Swarm Optimization Algorithm	ESOA	OriginalESOA	2022	2	medium
Swarm	Fox Optimizer	FOX	OriginalFOX	2023	4	easy
Swarm	Golden Jackal Optimization	GJO	OriginalGJO	2022	2	easy
Swarm	Giant Trevally Optimization	GTO	OriginalGTO	2022	4	medium
Swarm	*	*	Matlab101GTO	2022	2	medium
Swarm	*	*	Matlab102GTO	2023	2	hard
Swarm	Mountain Gazelle Optimizer	MGO	OriginalMGO	2022	2	easy
Swarm	Sea-Horse Optimization	SeaHO	OriginalSeaHO	2022	2	medium
***	***	***	***	***	***	***
Physics	Simulated Annealling	SA	OriginalSA	1983	9	medium
Physics	*	*	GaussianSA	*	5	medium
Physics	*	*	SwarmSA	1987	9	medium
Physics	Wind Driven Optimization	WDO	OriginalWDO	2013	7	easy
Physics	Multi*Verse Optimizer	MVO	OriginalMVO	2016	4	easy
Physics	*	*	BaseMVO	*	4	easy
Physics	Tug of War Optimization	TWO	OriginalTWO	2016	2	easy
Physics	*	*	OppoTWO	*	2	medium
Physics	*	*	LevyTWO	*	2	medium
Physics	*	*	EnhancedTWO	2020	2	medium
Physics	Electromagnetic Field Optimization	EFO	OriginalEFO	2016	6	easy
Physics	*	*	BaseEFO	*	6	medium
Physics	Nuclear Reaction Optimization	NRO	OriginalNRO	2019	2	hard*
Physics	Henry Gas Solubility Optimization	HGSO	OriginalHGSO	2019	3	medium
Physics	Atom Search Optimization	ASO	OriginalASO	2019	4	medium
Physics	Equilibrium Optimizer	EO	OriginalEO	2019	2	easy
Physics	*	*	ModifiedEO	2020	2	medium
Physics	*	*	AdaptiveEO	2020	2	medium
Physics	Archimedes Optimization Algorithm	ArchOA	OriginalArchOA	2021	8	medium
Physics	Chernobyl Disaster Optimization	CDO	OriginalCDO	2023	2	easy
Physics	Energy Valley Optimization	EVO	OriginalEVO	2023	2	medium
Physics	Fick's Law Algorithm	FLA	OriginalFLA	2023	8	hard
Physics	Physical Phenomenon of RIME-ice	RIME	OriginalRIME	2023	3	easy
***	***	***	***	***	***	***
Human	Culture Algorithm	CA	OriginalCA	1994	3	easy
Human	Imperialist Competitive Algorithm	ICA	OriginalICA	2007	8	hard*
Human	Teaching Learning*based Optimization	TLO	OriginalTLO	2011	2	easy
Human	*	*	BaseTLO	2012	2	easy
Human	*	*	ITLO	2013	3	medium
Human	Brain Storm Optimization	BSO	OriginalBSO	2011	8	medium
Human	*	*	ImprovedBSO	2017	7	medium
Human	Queuing Search Algorithm	QSA	OriginalQSA	2019	2	hard
Human	*	*	BaseQSA	*	2	hard
Human	*	*	OppoQSA	*	2	hard
Human	*	*	LevyQSA	*	2	hard
Human	*	*	ImprovedQSA	2021	2	hard
Human	Search And Rescue Optimization	SARO	OriginalSARO	2019	4	medium
Human	*	*	BaseSARO	*	4	medium
Human	Life Choice*Based Optimization	LCO	OriginalLCO	2019	3	easy
Human	*	*	BaseLCO	*	3	easy
Human	*	*	ImprovedLCO	*	2	easy
Human	Social Ski*Driver Optimization	SSDO	OriginalSSDO	2019	2	easy
Human	Gaining Sharing Knowledge*based Algorithm	GSKA	OriginalGSKA	2019	6	medium
Human	*	*	BaseGSKA	*	4	medium
Human	Coronavirus Herd Immunity Optimization	CHIO	OriginalCHIO	2020	4	medium
Human	*	*	BaseCHIO	*	4	medium
Human	Forensic*Based Investigation Optimization	FBIO	OriginalFBIO	2020	2	medium
Human	*	*	BaseFBIO	*	2	medium
Human	Battle Royale Optimization	BRO	OriginalBRO	2020	3	medium
Human	*	*	BaseBRO	*	3	medium
Human	Student Psychology Based Optimization	SPBO	OriginalSPBO	2020	2	medium
Human	*	*	DevSPBO	*	2	medium
Human	Heap-based Optimization	HBO	OriginalHBO	2020	3	medium
Human	Human Conception Optimization	HCO	OriginalHCO	2022	6	medium
Human	Dwarf Mongoose Optimization Algorithm	DMOA	OriginalDMOA	2022	4	medium
Human	*	*	DevDMOA	*	3	medium
Human	War Strategy Optimization	WarSO	OriginalWarSO	2022	3	easy
***	***	***	***	***	***	***
Bio	Invasive Weed Optimization	IWO	OriginalIWO	2006	7	easy
Bio	Biogeography*Based Optimization	BBO	OriginalBBO	2008	4	easy
Bio	*	*	BaseBBO	*	4	easy
Bio	Virus Colony Search	VCS	OriginalVCS	2016	4	hard*
Bio	*	*	BaseVCS	*	4	hard*
Bio	Satin Bowerbird Optimizer	SBO	OriginalSBO	2017	5	easy
Bio	*	*	BaseSBO	*	5	easy
Bio	Earthworm Optimisation Algorithm	EOA	OriginalEOA	2018	8	medium
Bio	Wildebeest Herd Optimization	WHO	OriginalWHO	2019	12	hard
Bio	Slime Mould Algorithm	SMA	OriginalSMA	2020	3	easy
Bio	*	*	BaseSMA	*	3	easy
Bio	Barnacles Mating Optimizer	BMO	OriginalBMO	2018	3	easy
Bio	Tunicate Swarm Algorithm	TSA	OriginalTSA	2020	2	easy
Bio	Symbiotic Organisms Search	SOS	OriginalSOS	2014	2	medium
Bio	Seagull Optimization Algorithm	SOA	OriginalSOA	2019	3	easy
Bio	*	*	DevSOA	*	3	easy
Bio	Brown-Bear Optimization Algorithm	BBOA	OriginalBBOA	2023	2	medium
Bio	Tree Physiology Optimization	TPO	OriginalTPO	2017	5	medium
***	***	***	***	***	***	***
System	Germinal Center Optimization	GCO	OriginalGCO	2018	4	medium
System	*	*	BaseGCO	*	4	medium
System	Water Cycle Algorithm	WCA	OriginalWCA	2012	5	medium
System	Artificial Ecosystem*based Optimization	AEO	OriginalAEO	2019	2	easy
System	*	*	EnhancedAEO	2020	2	medium
System	*	*	ModifiedAEO	2020	2	medium
System	*	*	ImprovedAEO	2021	2	medium
System	*	*	AugmentedAEO	2022	2	medium
***	***	***	***	***	***	***
Math	Hill Climbing	HC	OriginalHC	1993	3	easy
Math	*	*	SwarmHC	*	3	easy
Math	Cross-Entropy Method	CEM	OriginalCEM	1997	4	easy
Math	Tabu Search	TS	OriginalTS	2004	5	easy
Math	Sine Cosine Algorithm	SCA	OriginalSCA	2016	2	easy
Math	*	*	BaseSCA	*	2	easy
Math	*	*	QLE-SCA	2022	4	hard
Math	Gradient-Based Optimizer	GBO	OriginalGBO	2020	5	medium
Math	Arithmetic Optimization Algorithm	AOA	OrginalAOA	2021	6	easy
Math	Chaos Game Optimization	CGO	OriginalCGO	2021	2	easy
Math	Pareto-like Sequential Sampling	PSS	OriginalPSS	2021	4	medium
Math	weIghted meaN oF vectOrs	INFO	OriginalINFO	2022	2	medium
Math	RUNge Kutta optimizer	RUN	OriginalRUN	2021	2	hard
Math	Circle Search Algorithm	CircleSA	OriginalCircleSA	2022	3	easy
Math	Success History Intelligent Optimization	SHIO	OriginalSHIO	2022	2	easy
***	***	***	***	***	***	***
Music	Harmony Search	HS	OriginalHS	2001	4	easy
Music	*	*	BaseHS	*	4	easy
+++	+++	+++	+++	+++	+++	+++
WARNING	PLEASE CHECK PLAGIARISM BEFORE USING BELOW ALGORITHMS	*	*	*	*	*
Swarm	Coati Optimization Algorithm	CoatiOA	OriginalCoatiOA	2023	2	easy
Swarm	Fennec For Optimization	FFO	OriginalFFO	2022	2	easy
Swarm	Northern Goshawk Optimization	NGO	OriginalNGO	2021	2	easy
Swarm	Osprey Optimization Algorithm	OOA	OriginalOOA	2023	2	easy
Swarm	Pelican Optimization Algorithm	POA	OriginalPOA	2023	2	easy
Swarm	Serval Optimization Algorithm	ServalOA	OriginalServalOA	2022	2	easy
Swarm	Siberian Tiger Optimization	STO	OriginalSTO	2022	2	easy
Swarm	Tasmanian Devil Optimization	TDO	OriginalTDO	2022	2	easy
Swarm	Walrus Optimization Algorithm	WaOA	OriginalWaOA	2022	2	easy
Swarm	Zebra Optimization Algorithm	ZOA	OriginalZOA	2022	2	easy
Human	Teamwork Optimization Algorithm	TOA	OriginalTOA	2021	2	easy

References

A

• ABC - Artificial Bee Colony

  • OriginalABC: Karaboga, D. (2005). An idea based on honey bee swarm for numerical optimization (Vol. 200, pp. 1-10). Technical report-tr06, Erciyes university, engineering faculty, computer engineering department.

• ACOR - Ant Colony Optimization.

  • OriginalACOR: Socha, K., & Dorigo, M. (2008). Ant colony optimization for continuous domains. European journal of operational research, 185(3), 1155-1173.

• ALO - Ant Lion Optimizer

  • OriginalALO: Mirjalili S (2015). “The Ant Lion Optimizer.” Advances in Engineering Software, 83, 80-98. doi: 10.1016/j.advengsoft.2015.01.010
  • BaseALO: The developed version

• AEO - Artificial Ecosystem-based Optimization

  • OriginalAEO: Zhao, W., Wang, L., & Zhang, Z. (2019). Artificial ecosystem-based optimization: a novel nature-inspired meta-heuristic algorithm. Neural Computing and Applications, 1-43.
  • AugmentedAEO: Van Thieu, N., Barma, S. D., Van Lam, T., Kisi, O., & Mahesha, A. (2022). Groundwater level modeling using Augmented Artificial Ecosystem Optimization. Journal of Hydrology, 129034.
  • ImprovedAEO: Rizk-Allah, R. M., & El-Fergany, A. A. (2020). Artificial ecosystem optimizer for parameters identification of proton exchange membrane fuel cells model. International Journal of Hydrogen Energy.
  • EnhancedAEO: Eid, A., Kamel, S., Korashy, A., & Khurshaid, T. (2020). An Enhanced Artificial Ecosystem-Based Optimization for Optimal Allocation of Multiple Distributed Generations. IEEE Access, 8, 178493-178513.
  • ModifiedAEO: Menesy, A. S., Sultan, H. M., Korashy, A., Banakhr, F. A., Ashmawy, M. G., & Kamel, S. (2020). Effective parameter extraction of different polymer electrolyte membrane fuel cell stack models using a modified artificial ecosystem optimization algorithm. IEEE Access, 8, 31892-31909.

• ASO - Atom Search Optimization

  • OriginalASO: Zhao, W., Wang, L., & Zhang, Z. (2019). Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowledge-Based Systems, 163, 283-304.

• ArchOA - Archimedes Optimization Algorithm

  • OriginalArchOA: Hashim, F. A., Hussain, K., Houssein, E. H., Mabrouk, M. S., & Al-Atabany, W. (2021). Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems. Applied Intelligence, 51(3), 1531-1551.

• AOA - Arithmetic Optimization Algorithm

  • OriginalAOA: Abualigah, L., Diabat, A., Mirjalili, S., Abd Elaziz, M., & Gandomi, A. H. (2021). The arithmetic optimization algorithm. Computer methods in applied mechanics and engineering, 376, 113609.

• AO - Aquila Optimizer

  • OriginalAO: Abualigah, L., Yousri, D., Abd Elaziz, M., Ewees, A. A., Al-qaness, M. A., & Gandomi, A. H. (2021). Aquila Optimizer: A novel meta-heuristic optimization Algorithm. Computers & Industrial Engineering, 157, 107250.

• AVOA - African Vultures Optimization Algorithm

  • OriginalAVOA: Abdollahzadeh, B., Gharehchopogh, F. S., & Mirjalili, S. (2021). African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Computers & Industrial Engineering, 158, 107408.

• AGTO - Artificial Gorilla Troops Optimization

  • OriginalAGTO: Abdollahzadeh, B., Soleimanian Gharehchopogh, F., & Mirjalili, S. (2021). Artificial gorilla troops optimizer: a new nature‐inspired metaheuristic algorithm for global optimization problems. International Journal of Intelligent Systems, 36(10), 5887-5958.

• ARO - Artificial Rabbits Optimization:

  • OriginalARO: Wang, L., Cao, Q., Zhang, Z., Mirjalili, S., & Zhao, W. (2022). Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Engineering Applications of Artificial Intelligence, 114, 105082.

B

• BFO - Bacterial Foraging Optimization

  • OriginalBFO: Passino, K. M. (2002). Biomimicry of bacterial foraging for distributed optimization and control. IEEE control systems magazine, 22(3), 52-67.
  • ABFO: Nguyen, T., Nguyen, B. M., & Nguyen, G. (2019, April). Building resource auto-scaler with functional-link neural network and adaptive bacterial foraging optimization. In International Conference on Theory and Applications of Models of Computation (pp. 501-517). Springer, Cham.

• BeesA - Bees Algorithm

  • OriginalBeesA: Pham, D. T., Ghanbarzadeh, A., Koc, E., Otri, S., Rahim, S., & Zaidi, M. (2005). The bees algorithm. Technical Note, Manufacturing Engineering Centre, Cardiff University, UK.
  • ProbBeesA: The probabilitic version of: Pham, D. T., Ghanbarzadeh, A., Koç, E., Otri, S., Rahim, S., & Zaidi, M. (2006). The bees algorithm—a novel tool for complex optimisation problems. In Intelligent production machines and systems (pp. 454-459). Elsevier Science Ltd.

• BBO - Biogeography-Based Optimization

  • OriginalBBO: Simon, D. (2008). Biogeography-based optimization. IEEE transactions on evolutionary computation, 12(6), 702-713.
  • BaseBBO: The developed version

• BA - Bat Algorithm

  • OriginalBA: Yang, X. S. (2010). A new metaheuristic bat-inspired algorithm. In Nature inspired cooperative strategies for optimization (NICSO 2010) (pp. 65-74). Springer, Berlin, Heidelberg.
  • AdaptiveBA: Wang, X., Wang, W. and Wang, Y., 2013, July. An adaptive bat algorithm. In International Conference on Intelligent Computing(pp. 216-223). Springer, Berlin, Heidelberg.
  • ModifiedBA: Dong, H., Li, T., Ding, R. and Sun, J., 2018. A novel hybrid genetic algorithm with granular information for feature selection and optimization. Applied Soft Computing, 65, pp.33-46.

• BSO - Brain Storm Optimization

  • OriginalBSO: . Shi, Y. (2011, June). Brain storm optimization algorithm. In International conference in swarm intelligence (pp. 303-309). Springer, Berlin, Heidelberg.
  • ImprovedBSO: El-Abd, M., 2017. Global-best brain storm optimization algorithm. Swarm and evolutionary computation, 37, pp.27-44.

• BSA - Bird Swarm Algorithm

  • OriginalBSA: Meng, X. B., Gao, X. Z., Lu, L., Liu, Y., & Zhang, H. (2016). A new bio-inspired optimisation algorithm:Bird Swarm Algorithm. Journal of Experimental & Theoretical Artificial Intelligence, 28(4), 673-687.

• BMO - Barnacles Mating Optimizer:

  • OriginalBMO: Sulaiman, M. H., Mustaffa, Z., Saari, M. M., Daniyal, H., Daud, M. R., Razali, S., & Mohamed, A. I. (2018, June). Barnacles mating optimizer: a bio-inspired algorithm for solving optimization problems. In 2018 19th IEEE/ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD) (pp. 265-270). IEEE.

• BES - Bald Eagle Search

  • OriginalBES: Alsattar, H. A., Zaidan, A. A., & Zaidan, B. B. (2019). Novel meta-heuristic bald eagle search optimisation algorithm. Artificial Intelligence Review, 1-28.

• BRO - Battle Royale Optimization

  • OriginalBRO: Rahkar Farshi, T. (2020). Battle royale optimization algorithm. Neural Computing and Applications, 1-19.
  • BaseBRO: The developed version

C

• CA - Culture Algorithm

  • OriginalCA: Reynolds, R.G., 1994, February. An introduction to cultural algorithms. In Proceedings of the third annual conference on evolutionary programming (Vol. 24, pp. 131-139). River Edge, NJ: World Scientific.

• CEM - Cross Entropy Method

  • OriginalCEM: Rubinstein, R. (1999). The cross-entropy method for combinatorial and continuous optimization. Methodology and computing in applied probability, 1(2), 127-190.

• CSO - Cat Swarm Optimization

  • OriginalCSO: Chu, S. C., Tsai, P. W., & Pan, J. S. (2006, August). Cat swarm optimization. In Pacific Rim international conference on artificial intelligence (pp. 854-858). Springer, Berlin, Heidelberg.

• CSA - Cuckoo Search Algorithm

  • OriginalCSA: Yang, X. S., & Deb, S. (2009, December). Cuckoo search via Lévy flights. In 2009 World congress on nature & biologically inspired computing (NaBIC) (pp. 210-214). Ieee.

• CRO - Coral Reefs Optimization

  • OriginalCRO: Salcedo-Sanz, S., Del Ser, J., Landa-Torres, I., Gil-López, S., & Portilla-Figueras, J. A. (2014). The coral reefs optimization algorithm: a novel metaheuristic for efficiently solving optimization problems. The Scientific World Journal, 2014.
  • OCRO: Nguyen, T., Nguyen, T., Nguyen, B. M., & Nguyen, G. (2019). Efficient time-series forecasting using neural network and opposition-based coral reefs optimization. International Journal of Computational Intelligence Systems, 12(2), 1144-1161.

• COA - Coyote Optimization Algorithm

  • OriginalCOA: Pierezan, J., & Coelho, L. D. S. (2018, July). Coyote optimization algorithm: a new metaheuristic for global optimization problems. In 2018 IEEE congress on evolutionary computation (CEC) (pp. 1-8). IEEE.

• CHIO - Coronavirus Herd Immunity Optimization

  • OriginalCHIO: Al-Betar, M. A., Alyasseri, Z. A. A., Awadallah, M. A., & Abu Doush, I. (2021). Coronavirus herd immunity optimizer (CHIO). Neural Computing and Applications, 33(10), 5011-5042.
  • BaseCHIO: The developed version

• CGO - Chaos Game Optimization

  • OriginalCGO: Talatahari, S., & Azizi, M. (2021). Chaos Game Optimization: a novel metaheuristic algorithm. Artificial Intelligence Review, 54(2), 917-1004.

• CSA - Circle Search Algorithm

  • OriginalCSA: Qais, M. H., Hasanien, H. M., Turky, R. A., Alghuwainem, S., Tostado-Véliz, M., & Jurado, F. (2022). Circle Search Algorithm: A Geometry-Based Metaheuristic Optimization Algorithm. Mathematics, 10(10), 1626.

D

• DE - Differential Evolution

  • BaseDE: Storn, R., & Price, K. (1997). Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. Journal of global optimization, 11(4), 341-359.
  • JADE: Zhang, J., & Sanderson, A. C. (2009). JADE: adaptive differential evolution with optional external archive. IEEE Transactions on evolutionary computation, 13(5), 945-958.
  • SADE: Qin, A. K., & Suganthan, P. N. (2005, September). Self-adaptive differential evolution algorithm for numerical optimization. In 2005 IEEE congress on evolutionary computation (Vol. 2, pp. 1785-1791). IEEE.
  • SHADE: Tanabe, R., & Fukunaga, A. (2013, June). Success-history based parameter adaptation for differential evolution. In 2013 IEEE congress on evolutionary computation (pp. 71-78). IEEE.
  • L_SHADE: Tanabe, R., & Fukunaga, A. S. (2014, July). Improving the search performance of SHADE using linear population size reduction. In 2014 IEEE congress on evolutionary computation (CEC) (pp. 1658-1665). IEEE.
  • SAP_DE: Teo, J. (2006). Exploring dynamic cls-adaptive populations in differential evolution. Soft Computing, 10(8), 673-686.

• DSA - Differential Search Algorithm (not done)

  • BaseDSA: Civicioglu, P. (2012). Transforming geocentric cartesian coordinates to geodetic coordinates by using differential search algorithm. Computers & Geosciences, 46, 229-247.

• DO - Dragonfly Optimization

  • OriginalDO: Mirjalili, S. (2016). Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Computing and Applications, 27(4), 1053-1073.

• DMOA - Dwarf Mongoose Optimization Algorithm

  • OriginalDMOA: Agushaka, J. O., Ezugwu, A. E., & Abualigah, L. (2022). Dwarf mongoose optimization algorithm. Computer methods in applied mechanics and engineering, 391, 114570.
  • DevDMOA: The developed version

E

• ES - Evolution Strategies .

  • OriginalES: Schwefel, H. P. (1984). Evolution strategies: A family of non-linear optimization techniques based on imitating some principles of organic evolution. Annals of Operations Research, 1(2), 165-167.
  • LevyES: Zhang, S., & Salari, E. (2005). Competitive learning vector quantization with evolution strategies for image compression. Optical Engineering, 44(2), 027006.

• EP - Evolutionary programming .

  • OriginalEP: Fogel, L. J. (1994). Evolutionary programming in perspective: The top-down view. Computational intelligence: Imitating life.
  • LevyEP: Lee, C.Y. and Yao, X., 2001, May. Evolutionary algorithms with adaptive lévy mutations. In Proceedings of the 2001 congress on evolutionary computation (IEEE Cat. No. 01TH8546) (Vol. 1, pp. 568-575). IEEE.

• EHO - Elephant Herding Optimization .

  • OriginalEHO: Wang, G. G., Deb, S., & Coelho, L. D. S. (2015, December). Elephant herding optimization. In 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI) (pp. 1-5). IEEE.

• EFO - Electromagnetic Field Optimization .

  • OriginalEFO:Abedinpourshotorban, H., Shamsuddin, S. M., Beheshti, Z., & Jawawi, D. N. (2016). Electromagnetic field optimization: A physics-inspired metaheuristic optimization algorithm. Swarm and Evolutionary Computation, 26, 8-22.
  • BaseEFO: The developed version

• EOA - Earthworm Optimisation Algorithm .

  • OriginalEOA: Wang, G. G., Deb, S., & dos Santos Coelho, L. (2018). Earthworm optimisation algorithm: a bio-inspired metaheuristic algorithm for global optimisation problems. IJBIC, 12(1), 1-22.

• EO - Equilibrium Optimizer .

  • OriginalEO: Faramarzi, A., Heidarinejad, M., Stephens, B., & Mirjalili, S. (2019). Equilibrium optimizer: A novel optimization algorithm. Knowledge-Based Systems.
  • ModifiedEO: Gupta, S., Deep, K., & Mirjalili, S. (2020). An efficient equilibrium optimizer with mutation strategy for numerical optimization. Applied Soft Computing, 96, 106542.
  • AdaptiveEO: Wunnava, A., Naik, M. K., Panda, R., Jena, B., & Abraham, A. (2020). A novel interdependence based multilevel thresholding technique using adaptive equilibrium optimizer. Engineering Applications of Artificial Intelligence, 94, 103836.

F

• FFA - Firefly Algorithm

  • OriginalFFA: Łukasik, S., & Żak, S. (2009, October). Firefly algorithm for continuous constrained optimization tasks. In International conference on computational collective intelligence (pp. 97-106). Springer, Berlin, Heidelberg.

• FA - Fireworks algorithm

  • OriginalFA: Tan, Y., & Zhu, Y. (2010, June). Fireworks algorithm for optimization. In International conference in swarm intelligence (pp. 355-364). Springer, Berlin, Heidelberg.

• FPA - Flower Pollination Algorithm

  • OriginalFPA: Yang, X. S. (2012, September). Flower pollination algorithm for global optimization. In International conference on unconventional computing and natural computation (pp. 240-249). Springer, Berlin, Heidelberg.

• FOA - Fruit-fly Optimization Algorithm

  • OriginalFOA: Pan, W. T. (2012). A new fruit fly optimization algorithm: taking the financial distress model as an example. Knowledge-Based Systems, 26, 69-74.
  • BaseFOA: The developed version
  • WhaleFOA: Fan, Y., Wang, P., Heidari, A. A., Wang, M., Zhao, X., Chen, H., & Li, C. (2020). Boosted hunting-based fruit fly optimization and advances in real-world problems. Expert Systems with Applications, 159, 113502.

• FBIO - Forensic-Based Investigation Optimization

  • OriginalFBIO: Chou, J.S. and Nguyen, N.M., 2020. FBI inspired meta-optimization. Applied Soft Computing, p.106339.
  • BaseFBIO: Fathy, A., Rezk, H. and Alanazi, T.M., 2021. Recent approach of forensic-based investigation algorithm for optimizing fractional order PID-based MPPT with proton exchange membrane fuel cell.IEEE Access,9, pp.18974-18992.

• FHO - Fire Hawk Optimization

  • OriginalFHO: Azizi, M., Talatahari, S., & Gandomi, A. H. (2022). Fire Hawk Optimizer: a novel metaheuristic algorithm. Artificial Intelligence Review, 1-77.

G

• GA - Genetic Algorithm

  • BaseGA: Holland, J. H. (1992). Genetic algorithms. Scientific american, 267(1), 66-73.
  • SingleGA: De Falco, I., Della Cioppa, A. and Tarantino, E., 2002. Mutation-based genetic algorithm: performance evaluation. Applied Soft Computing, 1(4), pp.285-299.
  • MultiGA: De Jong, K.A. and Spears, W.M., 1992. A formal analysis of the role of multi-point crossover in genetic algorithms. Annals of mathematics and Artificial intelligence, 5(1), pp.1-26.
  • EliteSingleGA: Elite version of Single-point mutation GA
  • EliteMultiGA: Elite version of Multiple-point mutation GA

• GWO - Grey Wolf Optimizer

  • OriginalGWO: Mirjalili, S., Mirjalili, S. M., & Lewis, A. (2014). Grey wolf optimizer. Advances in engineering software, 69, 46-61.
  • RW_GWO: Gupta, S., & Deep, K. (2019). A novel random walk grey wolf optimizer. Swarm and evolutionary computation, 44, 101-112.
  • GWO_WOA: Obadina, O. O., Thaha, M. A., Althoefer, K., & Shaheed, M. H. (2022). Dynamic characterization of a master–slave robotic manipulator using a hybrid grey wolf–whale optimization algorithm. Journal of Vibration and Control, 28(15-16), 1992-2003.
  • IGWO: Kaveh, A. & Zakian, P.. (2018). Improved GWO algorithm for optimal design of truss structures. Engineering with Computers. 34. 10.1007/s00366-017-0567-1.

• GOA - Grasshopper Optimisation Algorithm

  • OriginalGOA: Saremi, S., Mirjalili, S., & Lewis, A. (2017). Grasshopper optimisation algorithm: theory and application. Advances in Engineering Software, 105, 30-47.

• GCO - Germinal Center Optimization

  • OriginalGCO: Villaseñor, C., Arana-Daniel, N., Alanis, A. Y., López-Franco, C., & Hernandez-Vargas, E. A. (2018). Germinal center optimization algorithm. International Journal of Computational Intelligence Systems, 12(1), 13-27.
  • BaseGCO: The developed version

• GSKA - Gaining Sharing Knowledge-based Algorithm

  • OriginalGSKA: Mohamed, A. W., Hadi, A. A., & Mohamed, A. K. (2019). Gaining-sharing knowledge based algorithm for solving optimization problems: a novel nature-inspired algorithm. International Journal of Machine Learning and Cybernetics, 1-29.
  • BaseGSKA: Mohamed, A.W., Hadi, A.A., Mohamed, A.K. and Awad, N.H., 2020, July. Evaluating the performance of adaptive GainingSharing knowledge based algorithm on CEC 2020 benchmark problems. In 2020 IEEE Congress on Evolutionary Computation (CEC) (pp. 1-8). IEEE.

• GBO - Gradient-Based Optimizer

  • OriginalGBO: Ahmadianfar, I., Bozorg-Haddad, O., & Chu, X. (2020). Gradient-based optimizer: A new metaheuristic optimization algorithm. Information Sciences, 540, 131-159.

H

• HC - Hill Climbing .

  • OriginalHC: Talbi, E. G., & Muntean, T. (1993, January). Hill-climbing, simulated annealing and genetic algorithms: a comparative study and application to the mapping problem. In [1993] Proceedings of the Twenty-sixth Hawaii International Conference on System Sciences (Vol. 2, pp. 565-573). IEEE.
  • SwarmHC: The developed version based on swarm-based idea (Original is single-solution based method)

• HS - Harmony Search .

  • OriginalHS: Geem, Z. W., Kim, J. H., & Loganathan, G. V. (2001). A new heuristic optimization algorithm:harmony search. simulation, 76(2), 60-68.
  • BaseHS: The developed version

• HHO - Harris Hawks Optimization .

  • OriginalHHO: Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M., & Chen, H. (2019). Harris hawks optimization: Algorithm and applications. Future Generation Computer Systems, 97, 849-872.

• HGSO - Henry Gas Solubility Optimization .

  • OriginalHGSO: Hashim, F. A., Houssein, E. H., Mabrouk, M. S., Al-Atabany, W., & Mirjalili, S. (2019). Henry gas solubility optimization: A novel physics-based algorithm. Future Generation Computer Systems, 101, 646-667.

• HGS - Hunger Games Search .

  • OriginalHGS: Yang, Y., Chen, H., Heidari, A. A., & Gandomi, A. H. (2021). Hunger games search:Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Systems with Applications, 177, 114864.

• HHOA - Horse Herd Optimization Algorithm (not done) .

  • BaseHHOA: MiarNaeimi, F., Azizyan, G., & Rashki, M. (2021). Horse herd optimization algorithm: A nature-inspired algorithm for high-dimensional optimization problems. Knowledge-Based Systems, 213, 106711.

• HBA - Honey Badger Algorithm:

  • OriginalHBA: Hashim, F. A., Houssein, E. H., Hussain, K., Mabrouk, M. S., & Al-Atabany, W. (2022). Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Mathematics and Computers in Simulation, 192, 84-110.

I

• IWO - Invasive Weed Optimization .

  • OriginalIWO: Mehrabian, A. R., & Lucas, C. (2006). A novel numerical optimization algorithm inspired from weed colonization. Ecological informatics, 1(4), 355-366.

• ICA - Imperialist Competitive Algorithm

  • OriginalICA: Atashpaz-Gargari, E., & Lucas, C. (2007, September). Imperialist competitive algorithm: an algorithm for optimization inspired by imperialistic competition. In 2007 IEEE congress on evolutionary computation (pp. 4661-4667). Ieee.

• INFO - weIghted meaN oF vectOrs:

  • OriginalINFO: Ahmadianfar, I., Heidari, A. A., Gandomi, A. H., Chu, X., & Chen, H. (2021). RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Systems with Applications, 181, 115079.

J

• JA - Jaya Algorithm
  • OriginalJA: Rao, R. (2016). Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. International Journal of Industrial Engineering Computations, 7(1), 19-34.
  • BaseJA: The developed version
  • LevyJA: Iacca, G., dos Santos Junior, V. C., & de Melo, V. V. (2021). An improved Jaya optimization algorithm with Levy flight. Expert Systems with Applications, 165, 113902.

K

L

• LCO - Life Choice-based Optimization
  • OriginalLCO: Khatri, A., Gaba, A., Rana, K. P. S., & Kumar, V. (2019). A novel life choice-based optimizer. Soft Computing, 1-21.
  • BaseLCO: The developed version
  • ImprovedLCO: The improved version using Gaussian distribution and Mutation Mechanism

M

• MA - Memetic Algorithm

  • OriginalMA: Moscato, P. (1989). On evolution, search, optimization, genetic algorithms and martial arts: Towards memetic algorithms. Caltech concurrent computation program, C3P Report, 826, 1989.

• MFO - Moth Flame Optimization

  • OriginalMFO: Mirjalili, S. (2015). Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowledge-based systems, 89, 228-249.
  • BaseMFO: The developed version

• MVO - Multi-Verse Optimizer

  • OriginalMVO: Mirjalili, S., Mirjalili, S. M., & Hatamlou, A. (2016). Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Computing and Applications, 27(2), 495-513.
  • BaseMVO: The developed version

• MSA - Moth Search Algorithm

  • OriginalMSA: Wang, G. G. (2018). Moth search algorithm: a bio-inspired metaheuristic algorithm for global optimization problems. Memetic Computing, 10(2), 151-164.

• MRFO - Manta Ray Foraging Optimization

  • OriginalMRFO: Zhao, W., Zhang, Z., & Wang, L. (2020). Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Engineering Applications of Artificial Intelligence, 87, 103300.

• MPA - Marine Predators Algorithm:

  • OriginalMPA: Faramarzi, A., Heidarinejad, M., Mirjalili, S., & Gandomi, A. H. (2020). Marine Predators Algorithm: A nature-inspired metaheuristic. Expert systems with applications, 152, 113377.

N

• NRO - Nuclear Reaction Optimization

  • OriginalNRO: Wei, Z., Huang, C., Wang, X., Han, T., & Li, Y. (2019). Nuclear Reaction Optimization: A novel and powerful physics-based algorithm for global optimization. IEEE Access.

• NMRA - Nake Mole-Rat Algorithm

  • OriginalNMRA: Salgotra, R., & Singh, U. (2019). The naked mole-rat algorithm. Neural Computing and Applications, 31(12), 8837-8857.
  • ImprovedNMRA: Singh, P., Mittal, N., Singh, U. and Salgotra, R., 2021. Naked mole-rat algorithm with improved exploration and exploitation capabilities to determine 2D and 3D coordinates of sensor nodes in WSNs. Arabian Journal for Science and Engineering, 46(2), pp.1155-1178.

O

P

• PSO - Particle Swarm Optimization

  • OriginalPSO: Eberhart, R., & Kennedy, J. (1995, October). A new optimizer using particle swarm theory. In MHS'95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science (pp. 39-43). Ieee.
  • PPSO: Ghasemi, M., Akbari, E., Rahimnejad, A., Razavi, S. E., Ghavidel, S., & Li, L. (2019). Phasor particle swarm optimization: a simple and efficient variant of PSO. Soft Computing, 23(19), 9701-9718.
  • HPSO_TVAC: Ghasemi, M., Aghaei, J., & Hadipour, M. (2017). New cls-organising hierarchical PSO with jumping time-varying acceleration coefficients. Electronics Letters, 53(20), 1360-1362.
  • C_PSO: Liu, B., Wang, L., Jin, Y. H., Tang, F., & Huang, D. X. (2005). Improved particle swarm optimization combined with chaos. Chaos, Solitons & Fractals, 25(5), 1261-1271.
  • CL_PSO: Liang, J. J., Qin, A. K., Suganthan, P. N., & Baskar, S. (2006). Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE transactions on evolutionary computation, 10(3), 281-295.

• PFA - Pathfinder Algorithm

  • OriginalPFA: Yapici, H., & Cetinkaya, N. (2019). A new meta-heuristic optimizer: Pathfinder algorithm. Applied Soft Computing, 78, 545-568.

• PSS - Pareto-like Sequential Sampling

  • OriginalPSS: Shaqfa, M., & Beyer, K. (2021). Pareto-like sequential sampling heuristic for global optimisation. Soft Computing, 25(14), 9077-9096.

Q

• QSA - Queuing Search Algorithm
  • OriginalQSA: Zhang, J., Xiao, M., Gao, L., & Pan, Q. (2018). Queuing search algorithm: A novel metaheuristic algorithm for solving engineering optimization problems. Applied Mathematical Modelling, 63, 464-490.
  • BaseQSA: The developed version
  • OppoQSA: Zheng, X. and Nguyen, H., 2022. A novel artificial intelligent model for predicting water treatment efficiency of various biochar systems based on artificial neural network and queuing search algorithm. Chemosphere, 287, p.132251.
  • LevyQSA: Abderazek, H., Hamza, F., Yildiz, A.R., Gao, L. and Sait, S.M., 2021. A comparative analysis of the queuing search algorithm, the sine-cosine algorithm, the ant lion algorithm to determine the optimal weight design problem of a spur gear drive system. Materials Testing, 63(5), pp.442-447.
  • ImprovedQSA: Nguyen, B.M., Hoang, B., Nguyen, T. and Nguyen, G., 2021. nQSV-Net: a novel queuing search variant for global space search and workload modeling. Journal of Ambient Intelligence and Humanized Computing, 12(1), pp.27-46.

R

• RUN - RUNge Kutta optimizer:
  • OriginalRUN: Ahmadianfar, I., Heidari, A. A., Gandomi, A. H., Chu, X., & Chen, H. (2021). RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Systems with Applications, 181, 115079.

S

• SA - Simulated Annealling OriginalSA: Kirkpatrick, S., Gelatt Jr, C. D., & Vecchi, M. P. (1983). Optimization by simulated annealing. science, 220(4598), 671-680. GaussianSA: Van Laarhoven, P. J., Aarts, E. H., van Laarhoven, P. J., & Aarts, E. H. (1987). Simulated annealing (pp. 7-15). Springer Netherlands. SwarmSA: My developed version

• SSpiderO - Social Spider Optimization

  • OriginalSSpiderO: Cuevas, E., Cienfuegos, M., ZaldíVar, D., & Pérez-Cisneros, M. (2013). A swarm optimization algorithm inspired in the behavior of the social-spider. Expert Systems with Applications, 40(16), 6374-6384.

• SOS - Symbiotic Organisms Search:

  • OriginalSOS: Cheng, M. Y., & Prayogo, D. (2014). Symbiotic organisms search: a new metaheuristic optimization algorithm. Computers & Structures, 139, 98-112.

• SSpiderA - Social Spider Algorithm

  • OriginalSSpiderA: James, J. Q., & Li, V. O. (2015). A social spider algorithm for global optimization. Applied Soft Computing, 30, 614-627.

• SCA - Sine Cosine Algorithm

  • OriginalSCA: Mirjalili, S. (2016). SCA: a sine cosine algorithm for solving optimization problems. Knowledge-Based Systems, 96, 120-133.
  • BaseSCA: Attia, A.F., El Sehiemy, R.A. and Hasanien, H.M., 2018. Optimal power flow solution in power systems using a novel Sine-Cosine algorithm. International Journal of Electrical Power & Energy Systems, 99, pp.331-343.

• SRSR - Swarm Robotics Search And Rescue

  • OriginalSRSR: Bakhshipour, M., Ghadi, M. J., & Namdari, F. (2017). Swarm robotics search & rescue: A novel artificial intelligence-inspired optimization approach. Applied Soft Computing, 57, 708-726.

• SBO - Satin Bowerbird Optimizer

  • OriginalSBO: Moosavi, S. H. S., & Bardsiri, V. K. (2017). Satin bowerbird optimizer: a new optimization algorithm to optimize ANFIS for software development effort estimation. Engineering Applications of Artificial Intelligence, 60, 1-15.
  • BaseSBO: The developed version

• SHO - Spotted Hyena Optimizer

  • OriginalSHO: Dhiman, G., & Kumar, V. (2017). Spotted hyena optimizer: a novel bio-inspired based metaheuristic technique for engineering applications. Advances in Engineering Software, 114, 48-70.

• SSO - Salp Swarm Optimization

  • OriginalSSO: Mirjalili, S., Gandomi, A. H., Mirjalili, S. Z., Saremi, S., Faris, H., & Mirjalili, S. M. (2017). Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Advances in Engineering Software, 114, 163-191.

• SFO - Sailfish Optimizer

  • OriginalSFO: Shadravan, S., Naji, H. R., & Bardsiri, V. K. (2019). The Sailfish Optimizer: A novel nature-inspired metaheuristic algorithm for solving constrained engineering optimization problems. Engineering Applications of Artificial Intelligence, 80, 20-34.
  • ImprovedSFO: Li, L.L., Shen, Q., Tseng, M.L. and Luo, S., 2021. Power system hybrid dynamic economic emission dispatch with wind energy based on improved sailfish algorithm. Journal of Cleaner Production, 316, p.128318.

• SARO - Search And Rescue Optimization

  • OriginalSARO: Shabani, A., Asgarian, B., Gharebaghi, S. A., Salido, M. A., & Giret, A. (2019). A New Optimization Algorithm Based on Search and Rescue Operations. Mathematical Problems in Engineering, 2019.
  • BaseSARO: The developed version using Levy-flight

• SSDO - Social Ski-Driver Optimization

  • OriginalSSDO: Tharwat, A., & Gabel, T. (2019). Parameters optimization of support vector machines for imbalanced data using social ski driver algorithm. Neural Computing and Applications, 1-14.

• SLO - Sea Lion Optimization

  • OriginalSLO: Masadeh, R., Mahafzah, B. A., & Sharieh, A. (2019). Sea Lion Optimization Algorithm. Sea, 10(5).
  • ImprovedSLO: The developed version
  • ModifiedSLO: Masadeh, R., Alsharman, N., Sharieh, A., Mahafzah, B.A. and Abdulrahman, A., 2021. Task scheduling on cloud computing based on sea lion optimization algorithm. International Journal of Web Information Systems.

• Seagull Optimization Algorithm

  • OriginalSOA: Dhiman, G., & Kumar, V. (2019). Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowledge-based systems, 165, 169-196.
  • DevSOA: The developed version

• SMA - Slime Mould Algorithm

  • OriginalSMA: Li, S., Chen, H., Wang, M., Heidari, A. A., & Mirjalili, S. (2020). Slime mould algorithm: A new method for stochastic optimization. Future Generation Computer Systems.
  • BaseSMA: The developed version

• SSA - Sparrow Search Algorithm

  • OriginalSSA: Jiankai Xue & Bo Shen (2020) A novel swarm intelligence optimization approach: sparrow search algorithm, Systems Science & Control Engineering, 8:1, 22-34, DOI: 10.1080/21642583.2019.1708830
  • BaseSSA: The developed version

• SPBO - Student Psychology Based Optimization

  • OriginalSPBO: Das, B., Mukherjee, V., & Das, D. (2020). Student psychology based optimization algorithm: A new population based optimization algorithm for solving optimization problems. Advances in Engineering software, 146, 102804.
  • DevSPBO: The developed version

• SCSO - Sand Cat Swarm Optimization

  • OriginalSCSO: Seyyedabbasi, A., & Kiani, F. (2022). Sand Cat swarm optimization: a nature-inspired algorithm to solve global optimization problems. Engineering with Computers, 1-25.

T

• TLO - Teaching Learning Optimization

  • OriginalTLO: Rao, R. V., Savsani, V. J., & Vakharia, D. P. (2011). Teaching–learning-based optimization: a novel method for constrained mechanical design optimization problems. Computer-Aided Design, 43(3), 303-315.
  • BaseTLO: Rao, R., & Patel, V. (2012). An elitist teaching-learning-based optimization algorithm for solving complex constrained optimization problems. International Journal of Industrial Engineering Computations, 3(4), 535-560.
  • ImprovedTLO: Rao, R. V., & Patel, V. (2013). An improved teaching-learning-based optimization algorithm for solving unconstrained optimization problems. Scientia Iranica, 20(3), 710-720.

• TWO - Tug of War Optimization

  • OriginalTWO: Kaveh, A., & Zolghadr, A. (2016). A novel meta-heuristic algorithm: tug of war optimization. Iran University of Science & Technology, 6(4), 469-492.
  • OppoTWO: Kaveh, A., Almasi, P. and Khodagholi, A., 2022. Optimum Design of Castellated Beams Using Four Recently Developed Meta-heuristic Algorithms. Iranian Journal of Science and Technology, Transactions of Civil Engineering, pp.1-13.
  • LevyTWO: The developed version using Levy-flight
  • ImprovedTWO: Nguyen, T., Hoang, B., Nguyen, G., & Nguyen, B. M. (2020). A new workload prediction model using extreme learning machine and enhanced tug of war optimization. Procedia Computer Science, 170, 362-369.

• TSA - Tunicate Swarm Algorithm

  • OriginalTSA: Kaur, S., Awasthi, L. K., Sangal, A. L., & Dhiman, G. (2020). Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Engineering Applications of Artificial Intelligence, 90, 103541.

• TSO - Tuna Swarm Optimization

  • OriginalTSO: Xie, L., Han, T., Zhou, H., Zhang, Z. R., Han, B., & Tang, A. (2021). Tuna swarm optimization: a novel swarm-based metaheuristic algorithm for global optimization. Computational intelligence and Neuroscience, 2021.

U

V

• VCS - Virus Colony Search
  • OriginalVCS: Li, M. D., Zhao, H., Weng, X. W., & Han, T. (2016). A novel nature-inspired algorithm for optimization: Virus colony search. Advances in Engineering Software, 92, 65-88.
  • BaseVCS: The developed version

W

• WCA - Water Cycle Algorithm

  • OriginalWCA: Eskandar, H., Sadollah, A., Bahreininejad, A., & Hamdi, M. (2012). Water cycle algorithm–A novel metaheuristic optimization method for solving constrained engineering optimization problems. Computers & Structures, 110, 151-166.

• WOA - Whale Optimization Algorithm

  • OriginalWOA: Mirjalili, S., & Lewis, A. (2016). The whale optimization algorithm. Advances in engineering software, 95, 51-67.
  • HI_WOA: Tang, C., Sun, W., Wu, W., & Xue, M. (2019, July). A hybrid improved whale optimization algorithm. In 2019 IEEE 15th International Conference on Control and Automation (ICCA) (pp. 362-367). IEEE.

• WHO - Wildebeest Herd Optimization

  • OriginalWHO: Amali, D., & Dinakaran, M. (2019). Wildebeest herd optimization: A new global optimization algorithm inspired by wildebeest herding behaviour. Journal of Intelligent & Fuzzy Systems, (Preprint), 1-14.

• WDO - Wind Driven Optimization

  • OriginalWDO: Bayraktar, Z., Komurcu, M., Bossard, J.A. and Werner, D.H., 2013. The wind driven optimization technique and its application in electromagnetics. IEEE transactions on antennas and propagation, 61(5), pp.2745-2757.

X

Y

Z

List of papers used MEALPY

• Min, J., Oh, M., Kim, W., Seo, H., & Paek, J. (2022, October). Evaluation of Metaheuristic Algorithms for TAS Scheduling in Time-Sensitive Networking. In 2022 13th International Conference on Information and Communication Technology Convergence (ICTC) (pp. 809-812). IEEE.
• Khozeimeh, F., Sharifrazi, D., Izadi, N. H., Joloudari, J. H., Shoeibi, A., Alizadehsani, R., ... & Islam, S. M. S. (2021). Combining a convolutional neural network with autoencoders to predict the survival chance of COVID-19 patients. Scientific Reports, 11(1), 15343.
• Rajesh, K., Jain, E., & Kotecha, P. (2022). A Multi-Objective approach to the Electric Vehicle Routing Problem. arXiv preprint arXiv:2208.12440.
• Sánchez, A. J. H., & Upegui, F. R. (2022). Una herramienta para el diseño de redes MSMN de banda ancha en líneas de transmisión basada en algoritmos heurísticos de optimización comparados. Revista Ingeniería UC, 29(2), 106-123.
• Khanmohammadi, M., Armaghani, D. J., & Sabri Sabri, M. M. (2022). Prediction and Optimization of Pile Bearing Capacity Considering Effects of Time. Mathematics, 10(19), 3563.
• Kudela, J. (2023). The Evolutionary Computation Methods No One Should Use. arXiv preprint arXiv:2301.01984.
• Vieira, M., Faia, R., Pinto, T., & Vale, Z. (2022, September). Schedule Peer-to-Peer Transactions of an Energy Community Using Particle Swarm. In 2022 18th International Conference on the European Energy Market (EEM) (pp. 1-6). IEEE.
• Bui, X. N., Nguyen, H., Le, Q. T., & Le, T. N. Forecasting PM. MINING SCIENCE ANDTECHNOLOGY (Russia), 111.
• Bui, X. N., Nguyen, H., Le, Q. T., & Le, T. N. (2022). Forecasting PM 2.5 emissions in open-pit minesusing a functional link neural network optimized by various optimization algorithms. Gornye nauki i tekhnologii= Mining Science and Technology (Russia), 7(2), 111-125.
• Doğan, E., & Yörükeren, N. (2022). Enhancement of Transmission System Security with Archimedes Optimization Algorithm.
• Ayub, N., Aurangzeb, K., Awais, M., & Ali, U. (2020, November). Electricity theft detection using CNN-GRU and manta ray foraging optimization algorithm. In 2020 IEEE 23Rd international multitopic conference (INMIC) (pp. 1-6). IEEE.
• Pintilie, L., Nechita, M. T., Suditu, G. D., Dafinescu, V., & Drăgoi, E. N. (2022). Photo-decolorization of Eriochrome Black T: process optimization with Differential Evolution algorithm. In PASEW-22, MESSH-22 & CABES-22 April 19–21, 2022 Paris (France). Eminent Association of Pioneers.
• LaTorre, A., Molina, D., Osaba, E., Poyatos, J., Del Ser, J., & Herrera, F. (2021). A prescription of methodological guidelines for comparing bio-inspired optimization algorithms. Swarm and Evolutionary Computation, 67, 100973.
• Gottam, S., Nanda, S. J., & Maddila, R. K. (2021, December). A CNN-LSTM Model Trained with Grey Wolf Optimizer for Prediction of Household Power Consumption. In 2021 IEEE International Symposium on Smart Electronic Systems (iSES)(Formerly iNiS) (pp. 355-360). IEEE.
• Darius, P. S., Devadason, J., & Solomon, D. G. (2022, December). Prospects of Ant Colony Optimization (ACO) in Various Domains. In 2022 4th International Conference on Circuits, Control, Communication and Computing (I4C) (pp. 79-84). IEEE.
• Ayub, N., Irfan, M., Awais, M., Ali, U., Ali, T., Hamdi, M., ... & Muhammad, F. (2020). Big data analytics for short and medium-term electricity load forecasting using an AI techniques ensembler. Energies, 13(19), 5193.
• Biundini, I. Z., Melo, A. G., Coelho, F. O., Honório, L. M., Marcato, A. L., & Pinto, M. F. (2022). Experimentation and Simulation with Autonomous Coverage Path Planning for UAVs. Journal of Intelligent & Robotic Systems, 105(2), 46.
• Yousaf, I., Anwar, F., Imtiaz, S., Almadhor, A. S., Ishmanov, F., & Kim, S. W. (2022). An Optimized Hyperparameter of Convolutional Neural Network Algorithm for Bug Severity Prediction in Alzheimer’s-Based IoT System. Computational Intelligence and Neuroscience, 2022.
• Xu, L., Yan, W., & Ji, J. (2023). The research of a novel WOG-YOLO algorithm for autonomous driving object detection. Scientific reports, 13(1), 3699.
• Costache, R. D., Arabameri, A., Islam, A. R. M. T., Abba, S. I., Pandey, M., Ajin, R. S., & Pham, B. T. (2022). Flood susceptibility computation using state-of-the-art machine learning and optimization algorithms.
• Del Ser, J., Osaba, E., Martinez, A. D., Bilbao, M. N., Poyatos, J., Molina, D., & Herrera, F. (2021, December). More is not always better: insights from a massive comparison of meta-heuristic algorithms over real-parameter optimization problems. In 2021 IEEE Symposium Series on Computational Intelligence (SSCI) (pp. 1-7). IEEE.
• Rustam, F., Aslam, N., De La Torre Díez, I., Khan, Y. D., Mazón, J. L. V., Rodríguez, C. L., & Ashraf, I. (2022, November). White Blood Cell Classification Using Texture and RGB Features of Oversampled Microscopic Images. In Healthcare (Vol. 10, No. 11, p. 2230). MDPI.
• Neupane, D., Kafle, S., Gurung, S., Neupane, S., & Bhattarai, N. (2021). Optimal sizing and financial analysis of a stand-alone SPV-micro-hydropower hybrid system considering generation uncertainty. International Journal of Low-Carbon Technologies, 16(4), 1479-1491.
• Liang, R., Le-Hung, T., & Nguyen-Thoi, T. (2022). Energy consumption prediction of air-conditioning systems in eco-buildings using hunger games search optimization-based artificial neural network model. Journal of Building Engineering, 59, 105087.
• He, Z., Nguyen, H., Vu, T. H., Zhou, J., Asteris, P. G., & Mammou, A. (2022). Novel integrated approaches for predicting the compressibility of clay using cascade forward neural networks optimized by swarm-and evolution-based algorithms. Acta Geotechnica, 1-16.
• Xu, L., Yan, W., & Ji, J. (2022). The research of a novel WOG-YOLO algorithm forautonomous driving object detection.
• Nasir Ayub, M. I., Awais, M., Ali, U., Ali, T., Hamdi, M., Alghamdi, A., & Muhammad, F. Big Data Analytics for Short and Medium Term Electricity Load Forecasting using AI Techniques Ensembler.
• Xie, C., Nguyen, H., Choi, Y., & Armaghani, D. J. (2022). Optimized functional linked neural network for predicting diaphragm wall deflection induced by braced excavations in clays. Geoscience Frontiers, 13(2), 101313.
• Hakemi, S., Houshmand, M., & Hosseini, S. A. (2022). A Dynamic Quantum-Inspired Genetic Algorithm with Lengthening Chromosome Size.
• Kashifi, M. T. City-Wide Crash Risk Prediction and Interpretation Using Deep Learning Model with Multi-Source Big Data. Available at SSRN 4329686.
• Nguyen, H., & Hoang, N. D. (2022). Computer vision-based classification of concrete spall severity using metaheuristic-optimized Extreme Gradient Boosting Machine and Deep Convolutional Neural Network. Automation in Construction, 140, 104371.
• Zheng, J., Lu, Z., Wu, K., Ning, G. H., & Li, D. (2020). Coinage-metal-based cyclic trinuclear complexes with metal–metal interactions: Theories to experiments and structures to functions. Chemical Reviews, 120(17), 9675-9742.
• Van Thieu, N., Barma, S. D., Van Lam, T., Kisi, O., & Mahesha, A. (2023). Groundwater level modeling using Augmented Artificial Ecosystem Optimization. Journal of Hydrology, 617, 129034.
• Mo, Z., Zhang, Z., Miao, Q., & Tsui, K. L. (2022). Intelligent Informative Frequency Band Searching Assisted by a Dynamic Bandit Tree Method for Machine Fault Diagnosis. IEEE/ASME Transactions on Mechatronics.
• Dangi, D., Chandel, S. T., Dixit, D. K., Sharma, S., & Bhagat, A. (2023). An Efficient Model for Sentiment Analysis using Artificial Rabbits Optimized Vector Functional Link Network. Expert Systems with Applications, 119849.
• Dey, S., Roychoudhury, R., Malakar, S., & Sarkar, R. (2022). An optimized fuzzy ensemble of convolutional neural networks for detecting tuberculosis from Chest X-ray images. Applied Soft Computing, 114, 108094.
• Mousavirad, S. J., & Alexandre, L. A. (2022). Population-based JPEG Image Compression: Problem Re-Formulation. arXiv preprint arXiv:2212.06313.
• Tsui, K. L. Intelligent Informative Frequency Band Searching Assisted by A Dynamic Bandit Tree Method for Machine Fault Diagnosis.
• Neupane, D. (2020). Optimal Sizing and Performance Analysis of Solar PV-Micro hydropower Hybrid System in the Context of Rural Area of Nepal (Doctoral dissertation, Pulchowk Campus).
• LaTorre, A., Molina, D., Osaba, E., Poyatos, J., Del Ser, J., & Herrera, F. Swarm and Evolutionary Computation.
• Vieira, M. A. (2022). Otimização dos custos operacionais de uma comunidade energética considerando transações locais em “peer-to-peer” (Doctoral dissertation).
• Toğaçar, M. (2022). Using DarkNet models and metaheuristic optimization methods together to detect weeds growing along with seedlings. Ecological Informatics, 68, 101519.
• Toğaçar, M. (2021). Detection of segmented uterine cancer images by Hotspot Detection method using deep learning models, Pigeon-Inspired Optimization, types-based dominant activation selection approaches. Computers in Biology and Medicine, 136, 104659.
• Khan, N. A Short Term Electricity Load and Price Forecasting Model Based on BAT Algorithm in Logistic Regression and CNN-GRU with WOA.
• Yelisetti, S., Saini, V. K., Kumar, R., & Lamba, R. (2022, May). Energy Consumption Cost Benefits through Smart Home Energy Management in Residential Buildings: An Indian Case Study. In 2022 IEEE IAS Global Conference on Emerging Technologies (GlobConET) (pp. 930-935). IEEE.
• Nguyen, H., Cao, M. T., Tran, X. L., Tran, T. H., & Hoang, N. D. (2022). A novel whale optimization algorithm optimized XGBoost regression for estimating bearing capacity of concrete piles. Neural Computing and Applications, 1-28.
• Hirsching, C., de Jongh, S., Eser, D., Suriyah, M., & Leibfried, T. (2022). Meta-heuristic optimization of control structure and design for MMC-HVdc applications. Electric Power Systems Research, 213, 108371.
• Amelin, V., Gatiyatullin, E., Romanov, N., Samarkhanov, R., Vasilyev, R., & Yanovich, Y. (2022). Black-Box for Blockchain Parameters Adjustment. IEEE Access, 10, 101795-101802.
• Ngo, T. Q., Nguyen, L. Q., & Tran, V. Q. (2022). Novel hybrid machine learning models including support vector machine with meta-heuristic algorithms in predicting unconfined compressive strength of organic soils stabilised with cement and lime. International Journal of Pavement Engineering, 1-18.
• Zhu, Y., & Iiduka, H. (2021). Unified Algorithm Framework for Nonconvex Stochastic Optimization in Deep Neural Networks. IEEE Access, 9, 143807-143823.
• Hakemi, S., Houshmand, M., KheirKhah, E., & Hosseini, S. A. (2022). A review of recent advances in quantum-inspired metaheuristics. Evolutionary Intelligence, 1-16.
• Das, A., Das, S. R., Panda, J. P., Dey, A., Gajrani, K. K., Somani, N., & Gupta, N. (2022). Machine learning based modelling and optimization in hard turning of AISI D6 steel with newly developed AlTiSiN coated carbide tool. arXiv preprint arXiv:2202.00596.
• Yelisetti, S., Saini, V. K., Kumar, R., Lamba, R., & Saxena, A. (2022). Optimal energy management system for residential buildings considering the time of use price with swarm intelligence algorithms. Journal of Building Engineering, 59, 105062.
• Valdés, G. T. (2022). Algoritmo para la detección de vehículos y peatones combinando CNN´ sy técnicas de búsqueda.
• Sallam, N. M., Saleh, A. I., Ali, H. A., & Abdelsalam, M. M. (2023). An efficient EGWO algorithm as feature selection for B-ALL diagnoses and its subtypes classification using peripheral blood smear images. Alexandria Engineering Journal, 68, 39-66.