-
Notifications
You must be signed in to change notification settings - Fork 89
Nemerle language (part 2)
Author: Chistyakov Vladislav Yuryevich
Original: http://rsdn.ru/article/Nemerle/TheNemerleLanuage-prt-2.xml
Translator: Pavel Klinov
Variables are used for storing intermediate results of calculations. For example, consider the code below, which is the program from the previous section converting temperature from Celsius into Fahrenheit:
using System.Console;
def fahrenheitToCelsius(fahrenheit)
{
5.0 / 9 * (fahrenheit - 32)
}
def loop(fahrenheit)
{
WriteLine("Fahrenheit: {0, 4} Celsius: {1, 5:##0.0}",
fahrenheit, fahrenheitToCelsius(fahrenheit));
match (fahrenheit >= 0 && fahrenheit < 300)
{
| true => loop(fahrenheit + 20);
| false => ()
}
}
loop(0);It can be rewritten to use a new variable, e.g., fahrenheit:
using System.Console;
def fahrenheitToCelsius(fahrenheit)
{
5.0 / 9 * (fahrenheit - 32)
}
mutable fahrenheit = 0;
def loop()
{
match (fahrenheit >= 0 && fahrenheit < 300)
{
| true =>
WriteLine("Fahrenheit: {0, 4} Celsius: {1, 5:##0.0}",
fahrenheit, fahrenheitToCelsius(fahrenheit));
fahrenheit = fahrenheit + 20;
loop();
| false => ()
}
}
loop();WARNING
Besides replacing an argument by the variable we also moved the WriteLine call (for console output) inside the first pattern of the match operator. This does not change the behavior unless the program gets an input number which lies outside of the 0..300 range. Nothing will be printed in that case.
In the example above, the variable “farenheit” is ’’mutable’’. It is ’’declared’’ in the following line:
mutable fahrenheit = 0;and can be used in the subsequent code. The ’’modifier’’ mutable implies that the value of the variable can be changed repeatedly after the initial assignment.
Type of the new variable can be specified at the declaration time:
mutable fahrenheit : int = 0;If the type is not specified the compiler will attempt to infer it based on how the variable is initialized or used (the same is true for arguments of local functions). In the above example the variable is initialized with 0 so its type is inferred as int.
In our example the variable is initialized at the declaration time, however, uninitialized variables can also be declared:
mutable fahrenheit;Such variables are initialized implicitly based on the default value for the inferred type. In our example the variable is used as an integer so its initial value will be 0, which is the default value for int.
Explicit type specification and initialization are orthogonal, so any combinations are possible.
Consider the following line of code:
fahrenheit = fahrenheit + 20;Here the variable’s value is changed. The variable is assigned the value of the expression on the right hand-side. Since the same variable also occurs in that expression it is substituted for the previous value (the one stored before the assignment). If, for example, the variable fahrenheit was previously zero, its value will be changed to 20 as after this expression is evaluated. If it was 20, it will become 40 and so forth.
All assignment expressions have type “void”. One consequence of this is that Nemerle does not allow assigning the result of the same expression to multiple variables (this is allowed in various C-like languages, e.g., C, C++, C#, etc.). An attempt to compile the following code:
mutable x : int;
x = fahrenheit = fahrenheit + 20;will lead to the following compile time error:
Error: expected int, got void in assigned value: void is not a subtype of intThis happens simply because the expression “fahrenheit = fahrenheit + 20” has type “void”.
Any variable is visible starting from its declaration and until the end of that block of code (recall that each block is encompassed in curly brackets). Consider the sample of ‘’pseudo-code’’ (i. e., not a real code, just its prototype) below which illustrates visibility of the variable “x”:
"x" is NOT visible
{
"x" is NOT visible
mutable x = 0;
{
"x" is visible
def func()
{
"x" is visible
}
}
"x" is visible
}
"x" is NOT visibleVariables declared in a block are visible inside ‘’any nested expressions’’ including ‘’local functions’’. Therefore, functions can access not only values passed through their arguments but also variables declared in outer blocks.
Our examples use recursion for iterating over data, but most programming languages provide special constructs for this task, called loops. The most basic kind of loop in C-like languages is “while”. Its syntax and semantics are very simple:
while (condition)
bodyHere “condition” is a Boolean expression (i.e., an expression with the type bool) and “body” is an expression which is going to be evaluated as long as the condition is true. The body expression can be a block which allows for combining multiple expressions inside a loop.
Body expressions in Nemerle must have the type void since loops cannot have return values.
As mention above, there are no loops as basic syntactic constructs in Nemerle, however, they, as many other things, can be expressed using macros. We will do so shortly.
Having rewritten the example for translating Celcius into Fahrenheit using a variable, we essentially converted the loop function into a kind of loop. Therefore we now can easily extract the looping code and put it into a new macro.
Open the file MyMacroses.n, which you created when following the examples from the previous article, and copy into it the following code:
public macro While(condition, body)
syntax ("while", "(", condition, ")", body)
{
<[
def loop() : void
{
match ($condition)
{
| true =>
$body;
loop();
| false => ()
}
}
loop();
]>
}The quasi-quoting code is very similar to the previous example with two exceptions. First, the condition in the match operation is replaced by “$condition : bool”. Second, the code responsible for modifying the variable fahrenheit and printing it to the screen is replaced by “$body”. Arguments of the While macro are actual values of “condition” and “body” placeholders. As you remember from the previous article, such values are expressions which are inserted into the quasi-quotation wherever the placeholders are references in the code (two such places are highlighted in red in the above example).
So, as you can see, all works the same as in the example with the && operator. Except that this macro actually introduces new syntax! Here is what this means.
We said above that applying a macro in the code may look either like a function or an operator call. Here we obviously prefer the former since loops have nothing to do with operators. However, if we rewrite this macro in a straightforward way, i.e., by using the macro While without the syntactic extension, it will look not quite the way we want it to:
using System.Console;
def fahrenheitToCelsius(fahrenheit)
{
5.0 / 9 * (fahrenheit - 32)
}
mutable fahrenheit = 0;
While(fahrenheit >= 0 && fahrenheit < 300,
{
WriteLine("Fahrenheit: {0, 4} Celsius: {1, 5:##0.0}",
fahrenheit, fahrenheitToCelsius(fahrenheit));
fahrenheit = fahrenheit + 20;
});Instead, we would much prefer to mimic the C-like syntax as closely as possible. This is exactly what is achieved by adding the following declaration for extending the syntax:
syntax ("while", "(", condition, ")", body)The declaration consists of the syntax keyword which is followed by the description of the new syntax. Such descriptions may include static constructs, like “while” and the curly brackets in this example, as well as arguments of the macro which are treated as sub-expressions. String literals, e.g., “while”, used to describe new syntax become new language keywords. In particular, this means that declaring variables or functions with the same name in the same scope will not be permitted.
HINT
Using macros requires that its namespace (i.e., the namespace in which the macro is defined) is made accessible via the using directive. All macros shown above are defined the global namespace and are globally accessible. However, it makes sense to put user-defined macros into specific namespaces so that they do not interfere with other macros as well as with variables and functions having the same names.
Thus, the following syntax description:
syntax ("while", "(", condition, ")", body)introduces new syntax which is precisely identical to the classical syntax of while loops:
while (condition)
bodyAfter compiling the new macro (file MyMacroses.n) and adding the new assembly (file MyMacroses.dll) to the main program, we may use the new syntax to rewrite our temperature conversion example in the following way:
using System.Console;
def fahrenheitToCelsius(fahrenheit)
{
5.0 / 9 * (fahrenheit - 32)
}
mutable fahrenheit = 0;
while (fahrenheit >= 0 && fahrenheit < 300)
{
WriteLine("Fahrenheit: {0, 4} Celsius: {1, 5:##0.0}",
fahrenheit, fahrenheitToCelsius(fahrenheit));
fahrenheit = fahrenheit + 20;
}This code is eventually translated into a recursive function but, from the end programmer perspective, it simply uses a loop which looks exactly the same as the familiar while loop in C or C++.
Clearly, it could be quite tedious to define such common constructs as the operators && and ||, the while loop and so on. Fortunately, they are included in the standard macro library NemerleMacros.dll which ships with the compiler. The source code is available for downloading here.
The standard macros provide a bit more functionality than our simple macro shown above. For instance, they allow using the break and continue keywords which are familiar to any C developer. Interestingly, as we will describe later, these keywords are also defined as macros.
All the examples above printed results to the screen right after the conversion. This might be handy is some cases but quite often it is required to get the full list of results for subsequent processing. For example, we might want to construct a list of temperature values in Celsius and then either output everything to console or process it in some other way.
Nemerle does not provide any built-in types for manipulating lists but it could be done by using certain user-defined types. Some of those, for example, arrays, are provided by the language type system (.Net or Mono) while others, e.g., dynamic arrays, are included in the standard .Net libraries or the standard Nemerle library (Nemerle.dll). An example of the latter is list[T] which is very easy to use and is perfectly suited for learning list processing in Nemerle.
NOTE
Nemerle supports special kinds of literals for initializing arrays and instances of list[T] with constant values. It also provides a special concatenation operator for merging list[T] objects (we will describe it shortly).
The following code is yet another version of our evergoing temperature conversion example , but this time it is based on lists:
using System.Console;
def fahrenheitToCelsius(fahrenheit)
{
5.0 / 9 * (fahrenheit - 32)
}
def convertFsToCs(fahrenheits)
{
match (fahrenheits)
{
| headFahrenheit :: tailFahrenheits => fahrenheitToCelsius(headFahrenheit) :: convertFsToCs(tailFahrenheits)
| _ => []
}
}
def fahrenheits = [0, 20, 40, 60, 80, 100, 120, 140, 160, 180,
200, 220, 240, 260, 280, 300];
def celsiuses = convertFsToCs(fahrenheits);
WriteLine(celsiuses);This program outputs only the resulting temperature values in Fahrenheit:
[-17,7777777777778, -6,66666666666667, 4,44444444444444, 15,5555555555556,
26,6666666666667, 37,7777777777778, 48,8888888888889, 60, 71,1111111111111,
82,2222222222222, 93,3333333333333, 104,444444444444, 115,555555555556,
126,666666666667, 137,777777777778, 148,888888888889]As you can see, the output is not pretty-printed but no worries, we will fix it later. Now, let’s dig deeper into the example.
The fahrenheitToCelsius function has not changes so it can be skipped. The convertFsToCs function is responsible for converting a list of integers (temperature values in Fahrenheit) into a list of reals (temperature values in Celsius). We will first examine how this function is used and then proceed to its implementation.
The following line defines an immutable variable referencing the list of temperature values (in Fahrenheit):
def fahrenheits = [0, 20, 40, 60, 80, 100, 120, 140, 160, 180,
200, 220, 240, 260, 280, 300];The def keyword in front of a variable’s name, e.g., fahrenheits, designates that the variable is immutable. Such variables can be thought of as names associated with values of corresponding expressions, e.g., the list expression.
NOTE
In this example, as well as in most other cases, we could have used a mutable variable, however, immutable variables are generally preferred. They help to avoid accidental bugs which arise from unintended modifications, which improves the overall robustness of the software.
Values of immutable variables are set at initialization and remain constant during their lifetime. However, it is important to realize that it is the variable that remains constant, not the object that it points to. If the object permits modifications, then it could be changed even if referenced via an immutable variable.
It is possible to indicate type when declaring a new immutable variable. In the following example we declare and initialize the new variable y of type double.
def y : double = 10;It is initialized with 10. The literal 10 has type int but, since it is assigned to a variable of type double, it is implicitly casted to double. Such type conversion are always performed in compile time which means that first, there is no overhead at run time, and second, the compiler guarantees safety, i.e., all type errors are reported during compilation.
Nemerle imposes the following restrictions on variable names:
1. Names are composed of letters, numbers, and underscore symbols. The leading symbol must be either a letter or underscore.
2. Names are case-sensitive which means, for example, that «test» , «Test» , «TeSt» , «teSt» are considered distinct. The most common conventions for type names, type members, macros, and other public names in Nemerle are the “camel notation”, where all words in a name begin with a capital letter, or the “Pascal notation”, according to which even the first letter is capitalized. Keywords, both built-in and introduced via macros, are generally in lower case, even when composed of two or more words, (e.g. “foreach”)
3. Variable names should not coincide with keywords since the latter are reserved.
Reserved keywords in Nemerle
_, abstract, and, array, as, base, catch, class, def, delegate, enum, event, extern, false, finally, fun, implements, interface, internal, is, macro, match, matches, module, mutable, namespace, new, null, out, override, params, partial, private, protected, public, ref, sealed, static, struct, syntax, this, throw, true, try, type, typeof, using, variant, virtual, void, volatile, when, where, with
This list does not include keywords imported from macro libraries (including the standard library).
4. Names can begin with @ which indicates that the current token is a name and not a keyword. Therefore, this prefix allows for using any names for variable, function, and macro’s names, including the reserved ones, thus helping to lift the restriction described in 3. For example, @false is a perfectly valid variable’s name whereas false is not. Obviously, one would have to prepend @ to this name in all places in the code, however, in all languages where it is not a keyword it will be visible as false and not as @false (in other words, the compiler internally ignores the @ prefix). Another place where @ is ignored is meta-data which we will describe towards the end of this article.
Constructs of the form [comma separated list of values] are called list literals. Each such literal describes a statically defined list (i.e., a list whose elements are known at compile time). Lists are always ordered from left to right, so the literal [0, 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300] defines the list made of the numbers 0, 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300. A reference to this list is stored in the variable fahrenheits.
Lists can be constructed in the following ways:
1. via list literals (as in the example above)
2. via the concatenation operator :: also called list constructor
3. via the macro-defined operator ::= which is implemented on the basis of ::
4. via special constructs called list comprehensions. They are macros based on concatenation.
Concatenation allows for prepending single elements to the beginning of a list. Concatenation always returns values of the type list which allows for using it several times in a single expression.
For example, consider the list with three elements: 1, 2, and 3. It can be constructed via the following list literal:
[1, 2, 3]Or by using the list constructor:
1 :: 2 :: 3 :: []The last construct [] is a literal describing the empty list. Empty lists can only be represented via literals or by explicitly invoking list[T].Nil(). We will describe the latter option after we have introduced objects.
The list constructor is right associative, so the example above is equivalent to the following:
1 :: (2 :: (3 :: []))as opposed to:
((1 :: 2) :: 3) :: []This is quite important since internally lists are implemented as singly linked lists in which every element points to the next. The last element points to a special object denoted as [].
In the next example we define another immutable variable (celsiuses) that references a list of temperature values (in Celsius) constructed by applying the fahrenheitToCelsius function to all elements of the fahrenheits list which is passed as an argument.
def celsiuses = convertFsToCs(fahrenheits);Finally, the line
WriteLine(celsiuses);simply prints the list to console (this function must be familiar by now so we omit the details).
Now we move to the most interesting (and difficult) part of this example, convertFsToCs function, as shown below:
def convertFsToCs(fahrenheits)
{
match (fahrenheits)
{
| headFahrenheit :: tailFahrenheits => fahrenheitToCelsius(headFahrenheit) :: convertFsToCs(tailFahrenheits)
| _ => []
}
}HINT
Take a deep breath before moving forward if you have no experience with other functional languages. You are going to explore a few concepts which might appear bizarre not only to amateurs but even developers with fair experience in imperative programming, e.g., writing code in C, C++, C#, Java, Pascal, etc. The function being described uses the familiar match operator, however, in a bit more advanced way.
Here we the list constructor :: in the pattern. The following pattern:
| headFahrenheit :: tailFahrenheits =>means that the list is treated as if it contains at least one head element (headFahrenheit) and the tail, which is also a list (tailFahrenheits). The tail is just an arbitrary list, for example, It could well be empty []. Consequently, the pattern matches all lists containing at least one element and binds its head and tail to the variables headFahrenheit and tailFahrenheits respectively.
In other words, this pattern ’’decomposes’’ the list. This is in a sense the inverse of list construction since applying the constructor to the decomposed version restores the original list (see the example below).
| headFahrenheit :: tailFahrenheits => headFahrenheit :: tailFahrenheitsNOTE
The power of the pattern matching operator (match) mostly stems from the fact that it is capable of matching various object types based on patterns specified in their constructors. In other words, it describes an object which is then used for matching other objects. In later sections we will this operator for dealing with a number of different types and patterns to illustrate its capabilities.
Thus, the following pattern:
| headFahrenheit :: tailFahrenheits =>matches any non-empty list, binds it head to the variable headsFahrenheit and its tail (i.e., the remainder) to tailFahrenheits. This enables application of the conversion function, i.e., fahrenheitToCelsius, to the head of the list and the following recursive application of convertFsToCs to its tail.
fahrenheitToCelsius(headFahrenheit) :: convertFsToCs(tailFahrenheits)On the next iteration the variable fahrenheits will refer to the tail of the list and the same pattern will be matched. The process will continue until the list is empty. At that point the pattern headFahrenheit :: tailFahrenheits will not match the list so the next one, namely,
| _ =>That is to say, the function fahrenheitToCelsius is consequently applied to every element of the original list and its return value is prepended to the list constructed as a result of applying convertFsToCs to the tail of fahrenheits. Therefore the overall result is again a list whose length is that of the original list and each element is the converted into Celsius value of the corresponding element in fahrenheits.
HINT
Variable binding in pattern matching may appear weird to those developers who have previously used only imperative languages and are unfamiliar with functional programming. They are used to explicit variable declaration while each pattern declares its variables implicitly. Every name inside a pattern declares a variable so the value of the expression being matched can be bound to it. Understanding this fact might require some changes in how developers think about programs and even reconsidering certain basic principles which no longer work.
Few more words about expressiveness.
The example is already quite short but can still be improved. First, we can slightly change the representation of the list by moving from
def fahrenheits = [0, 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300];to:
def fahrenheit = $[0, 20 .. 300];The construct $[0, 20 .. 300] belongs to the list comprehensions family. List comprehensions is a macro that helps to simplify list generation and processing. In this particular example we use list comprehensions expression which generates the sequence of numbers by following a given pattern. This pattern works only for lists containing numbers. The first number in the expression defines the first element, the second number defines the second element as well as the difference between two consecutive elements. Finally, the number following .. defines a stopping condition, i.e., the value which the last element must not exceed. For example, consider the following expression:
$[1, 3 .. 10]It will generate the following list:
[1, 3, 5, 7, 9]while the expression
$[1, 3 .. 11]will produce
[1, 3, 5, 7, 9, 11]If the second element is omitted then the difference of 1 will be used, so the expression
$[1 .. 5]generates
[1, 2, 3, 4, 5]Generation of decreasing sequences is equally simply: the second argument must be less than the first and the last number must be less than the second. For instance, the expression shown below
$[5, 4 .. -5]will produce
[5, 4, 3, 2, 1, 0, -1, -2, -3, -4, -5]This looks quite similar to what most of you must have learned about number sequences in middle school.
Let us explicitly specify all types used in the convertFsToCs function for better understanding.
def convertFsToCs(fahrenheits : list[int]) : list[double]
{
match (fahrenheits)
{
| headFahrenheit : int :: tailFahrenheits : list[int] =>
fahrenheitToCelsius(headFahrenheit) : double :: convertFsToCs(tailFahrenheits) : list[double]
| [] => [] : list[double]
}
}For clarity we will put some type qualifications in parentheses as shown below:
def convertFsToCs(fahrenheits : list[int]) : list[double]
{
match (fahrenheits)
{
| (headFahrenheit : int) :: (tailFahrenheits : list[int]) =>
(fahrenheitToCelsius(headFahrenheit) : double) :: (convertFsToCs(tailFahrenheits) : list[double])
| [] => [] : list[double]
}
}The first thing which might confuse you is the construct like list[int] or list[double]. In the both cases the first token is a type name (“list”) while the one enclosed in the brackets is a type argument. The type list has a single argument which defines the type of stored elements.
One list cannot store elements of more than one type, e.g., numbers and strings, or numbers and floats. This restriction helps to avoid bugs and maximize runtime performance.
Type arguments are also types. Each type can have multiple arguments. In most cases Nemerle’s compiler can infer types for arguments. For instance, it was able to infer all types in the original examples in which no type was specified explicitly.
Also, Nemerle allows partial specification of types for local functions and variables. In particular, it is permitted to use the placeholder _ instead of a type. For example, one may specify a type while omitting a type argument:
expression : list[_]It is quite convenient when in those cases when the concrete type is unknown but the compiler should expect a type with single type argument. The following example is of the same kind but with three type arguments:
expression : X[_, _, _]The compiler will attempt to infer types for all placeholders but will raise an error if the structure of the type being inferred (i.e., the number of arguments) does not match the structure specified in the code. In addition, using placeholders allows for giving hints to the compiler without listing type arguments explicitly. This may help it to distinguish between types with the same name but with different number of arguments.
If the body of a function is just a single match expression and all arguments are passed inside that match then the match operator can be omitted. This means that the original implementation of convertFsToCs (see below):
def convertFsToCs(fahrenheits)
{
match (fahrenheits)
{
| headFahrenheit :: tailFahrenheits =>
fahrenheitToCelsius(headFahrenheit) :: convertFsToCs(tailFahrenheits)
| _ => []
}
}can be simplified to:
def convertFsToCs(fahrenheits)
{
| headFahrenheit :: tailFahrenheits =>
fahrenheitToCelsius(headFahrenheit) :: convertFsToCs(tailFahrenheits)
| _ => []
}The compiler should realize what is going on here and generate the same code as with explicit match. Therefore the latter example is just a terser equivalent of the former.
The function convertFsToCs is not universal because of using the specialized function fahrenheitToCelsius (declared above). However, it carries out a very common task: transforming one list into another by applying a certain function to every element of the original list.
NOTE
In mathematics such operations are often called mappings (of one list into another).
Next we will create a universally applicable analogue of convertFsToCs function. It will accept the conversion function as an argument (the same way as a list in the convertFsToCs function in the example above).
def convertFsToCs(fahrenheits, elementConverter)
{
match (fahrenheits)
{
| headFahrenheit :: tailFahrenheits =>
elementConverter(headFahrenheit) :: convertFsToCs(tailFahrenheits, elementConverter)
| _ => []
}
}Now it makes sense to rename the function, its arguments, and local variables to reflect its more general nature. Here is the updated version:
def convert(sourceList, elementConverter)
{
match (sourceList)
{
| head :: tail => elementConverter(head) :: convert(tail, elementConverter)
| _ => []
}
}HINT
The generic version may well appear easier to understand. This could be due to shorter (but no less meaningful) argument and variable names, as well as its declarative nature. The function is now separated from any of the use cases which clarifies its behavior.
The next listing demonstrates how the generic function could be used in the original example:
using System.Console;
def convert(sourceList, elementConverter)
{
match (sourceList)
{
| head :: tail => elementConverter(head) :: convert(tail, elementConverter)
| _ => []
}
}
def fahrenheitToCelsius(fahrenheit)
{
5.0 / 9 * (fahrenheit - 32)
}
def fahrenheits = $[0, 20 .. 300];
def celsiuses = convert(fahrenheits, fahrenheitToCelsius);
WriteLine(celsiuses);Note the second argument of the “convert” function. It is used to pass a reference to the conversion function “fahrenheitToCelsius”.
NOTE
We deliberately declared the “convert” function before the “fahrenheitToCelsius” function in order to prevent the first one to invoke the second one directly.
Now the function “convert” can be used for converting any kinds of lists using any applicable function. Functions having such property are often called universal.
NOTE
Functions which take other functions as input (or return other functions) are called higher-order functions (HOF).
However, an attempt to use the same function for the inverse transformation (Fahrenheit to Celsius) leads to an error saying that actual argument type (list[double]) does not match the declared type (list[int]). See the example:
def fahrenheits = $[0, 20 .. 300];
def celsiuses = convert(fahrenheits, fahrenheitToCelsius);
def celsiusToFahrenheit(celsius)
{
celsius * 9.0 / 5 + 32
}
def fahrenheits2 = convert(celsiuses, celsiusToFahrenheit);The problem might be easier to understand when all types (which are normally inferred by the compiler) are specified explicitly:
def convert(sourceList : list[int], elementConverter : int -> double) : list[double]
{
match (sourceList)
{
| head :: tail => elementConverter(head) :: convert(tail, elementConverter)
| _ => []
}
}NOTE
One question you may ask here is “how does the compiler infer types if there is no type information in the function’s body?” In such cases the compiler infers arguments’ types and the return value’s type based on how the function is first invoked. It searches through the source code for the first occurrence of the function, analyzes types of the passed arguments and uses that information to make inferences.
The first thing to note is the construct “int → double” which specifies the type of the function. The type to the left of the arrow specifies the argument type whereas the one to the right is the return type. All together it means that only functions which take an integer and return a double can be passed as arguments.
The issue here is that the original list storing values in Celsius has the type list[int] while the resulting list is a list of doubles (list[double]). We cannot pass the resulting list back to the function convert, nor can we pass a function of type double → double or double → int as the second argument. Does this mean we will be forced to create multiple versions of the same function, one for each combination of list types?
Fortunately not since Nemerle supports generic programming. This allows to abstract from concrete types by introducing a type parameter of a function (or a type). An example is shown below:
def convert[TInputElem, TOutputElem](
sourceList : list[TInputElem],
elementConverter : TInputElem -> TOutputElem
) : list[TOutputElem]
{
match (sourceList)
{
| head :: tail => elementConverter(head) :: convert(tail, elementConverter)
| _ => []
}
}Let’s take this to pieces. Enclosed in the square brackets is the specification of two type parameters, TInputElem and TOutputElem. Those are abstract type names which can be used in place of actual types in the function declaration. Each type name can be substituted by a single type. Type parameters can be arbitrary token; the only thing to be ensured is their uniqueness, i.e., they should not match any other types visible at the point of declaration.
NOTE
It was necessary to use two type parameters for convert function because elements of the original and the resulting lists can differ. However, just one type parameter might suffice in a situation when the used conversion function changes only values, but not types of the elements.
Generic functions can be used in exactly the same way as other functions:
using System.Console;
def convert[TInputElem, TOutputElem](
sourceList : list[TInputElem],
elementConverter : TInputElem -> TOutputElem
) : list[TOutputElem]
{
match (sourceList)
{
| head :: tail => elementConverter(head) :: convert(tail, elementConverter)
| _ => []
}
}
def fahrenheitToCelsius(fahrenheit)
{
5.0 / 9 * (fahrenheit - 32)
}
def fahrenheits = $[0, 20 .. 300];
def celsiuses = convert(fahrenheits, fahrenheitToCelsius);
WriteLine(celsiuses);A compiler will infer types for type parameters for all invocations of the convert function.
The next example shows that this generic function can be used for lists of any types. Here we add the inverse conversion (i.e., Fahrenheit to Celsius) to the previous example:
using System.Console;
def convert[TInputElem, TOutputElem](
sourceList : list[TInputElem],
elementConverter : TInputElem -> TOutputElem
) : list[TOutputElem]
{
match (sourceList)
{
| head :: tail => elementConverter(head) :: convert(tail, elementConverter)
| _ => []
}
}
def fahrenheitToCelsius(fahrenheit)
{
5.0 / 9 * (fahrenheit - 32)
}
def fahrenheits = $[0, 20 .. 300];
def celsiuses = convert(fahrenheits, fahrenheitToCelsius);
WriteLine(celsiuses);
// The inverse conversion
def celsiusToFahrenheit(celsius)
{
celsius * 9.0 / 5 + 32
}
def fahrenheits2 = convert(celsiuses, celsiusToFahrenheit);
WriteLine(fahrenheits2); // Celsius list converted back to Fahrenheit
WriteLine(fahrenheits); // The original list (compare them!)This code will print the following:
[-17,7777777777778, -6,66666666666667, 4,44444444444444, 15,5555555555556,
26,6666666666667, 37,7777777777778, 48,8888888888889, 60, 71,1111111111111,
82,2222222222222, 93,3333333333333, 104,444444444444, 115,555555555556,
126,666666666667, 137,777777777778, 148,888888888889]
[0, 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300]
[0, 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300]NOTE
Note the text following the double slash. This is an example of single line comments, which begin after a double slash and continue till the end of the line. As in other languages, a compiler will ignore such strings so they can safely be used for commenting the code or for temporary exclusion of certain blocks of code.
The lists fahrenheits and celsiuses are of different types. The former has type list[int] while the latter – list[double]. Nonetheless, the code compiles and runs as expected.
Homework
Specify all types for the arguments of the convert function.
NOTE
Figure 1 illustrates how an IDE displays information about a specific invocation of convert (IDE will be discussed in more detail later). Note the second line in the tooltip which begins with “Inferred:”. It shows the inferred type of the function in which all type parameters have been replaced by actual types inferred by the compiler.
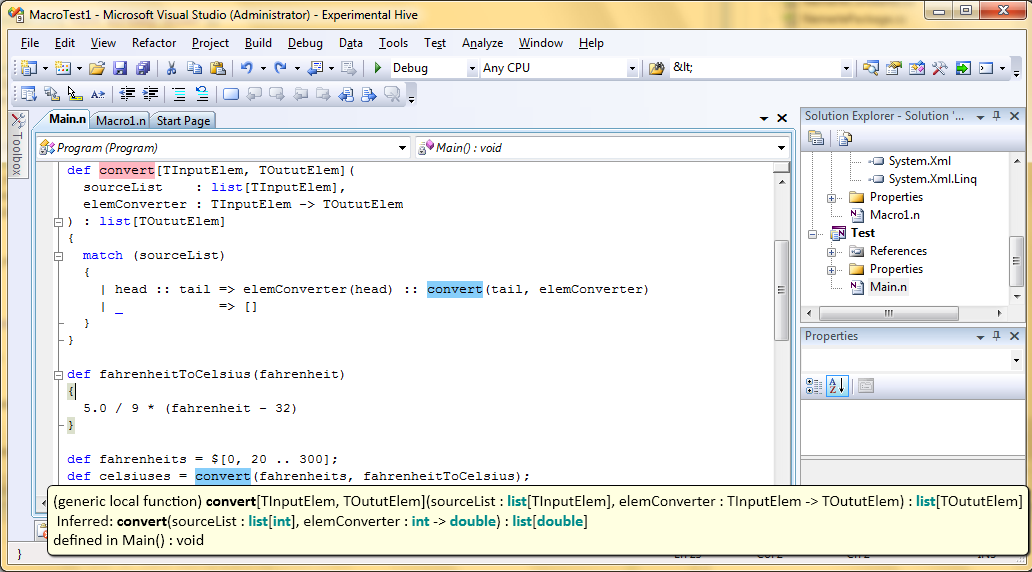
Figure 1. The information about the “convert” function displayed in the IDE.
Functions similar to convert are commonly used in Nemerle, so the language developers had taken them out into a separate library Nemerle.dll, which is automatically linked to all Nemerle programs. The analogue of convert provided by that library is called Map. It is a global function defined in the module NList which belongs to Nemerle.Collections namespace.
The listing below shows our temperature conversion code which now uses the library function Map.
using System.Console;
using Nemerle.Collections;
def fahrenheitToCelsius(fahrenheit)
{
5.0 / 9 * (fahrenheit - 32)
}
def fahrenheits = $[0, 20 .. 300];
def celsiuses = NList.Map(fahrenheits, fahrenheitToCelsius);
WriteLine(celsiuses);The module NList provides a variety of functions which simplify manipulations of lists (list[T]). Most of them are implemented either as global functions or as methods while some are available as methods only.
The principal difference between a method and function is that the former belongs to a type and is invoked via that type (i.e., using the “type_name.method_name” convention). Our example can be adapted to use a method as follows:
using System.Console;
def fahrenheitToCelsius(fahrenheit)
{
5.0 / 9 * (fahrenheit - 32)
}
def fahrenheits = $[0, 20 .. 300];
def celsiuses = fahrenheits.Map(fahrenheitToCelsius);
WriteLine(celsiuses);Here the list is passed to the method as an implicit parameter.
It is common to say that an object provides methods. For example, a list object provides Map as well as many other methods.
NOTE
Some of you may wonder whether there is any need in method given that they are so similar to functions. We will expand on this point in the section devoted to user-defined types.
HINT
Are there any guidelines for choosing methods or global functions? I personally tend to use methods due to the following reasons:
1. Using method does not require their namespaces be open. Observe that in the example using the function NList.Map the namespace Nemerle.Collections is explicitly open while it is not necessary for the example using the method Map.
2. Referring to methods is somewhat shorter syntactically since it is not needed to specify the module. Of course, it is still possible to explicitly make the module visible (i.e., via the “using” directive) to invoke its functions in the same way, but in that case all its content will become visible which might lead to name clashes. In contrast to functions, method names are always treated in the context of the enclosing type so name clashes do not occur.
3. Methods always belong to a specific object. This enables code completion in the IDE, i.e., getting the full list of methods just by entering a period following a variable’s name and pressing «Ctrl+Space».
You may have noticed that readability of the output declined quite substantially since we started using lists in our example. Now it is time to fix it without giving up on lists.
All we need to do is to union both lists (Celsius and Fahrenheit) into a new list, iterate over the latter, and print its elements to console in the same way as in the previous article. This is done in the example below:
def fahrenheitToCelsius(fahrenheit)
{
5.0 / 9 * (fahrenheit - 32)
}
def fahrenheits = $[0, 20 .. 300];
def celsiuses = fahrenheits.Map(fahrenheitToCelsius);
foreach ((fahrenheit, celsius) in fahrenheits.Zip(celsiuses))
WriteLine("Fahrenheit: {0, 4} Celsius: {1, 5:##0.0}", fahrenheit, celsius);WARNING
This example requires the standard macro library to compile, so you cannot use the compiler option “-nostdmacros”. The library provides the macros && and while so you also cannot use our library MyMacroses.dll which contains macros with the same names. To sum up, the command line for compiling this example should be “ncc -no-color f2c.n -out:f2c.exe”.
The code appears to be very similar to the previous version but that is deceptive. It is new in quite a few aspects.
First is the method “Zip”. It takes the second list as an argument and combines every element of the first list with every element of the second thus returning a list of pairs.
Second, the list returned by Zip is made up of tuples, the type we have not used so far. “Tuple” is an immutable data type which allows storing two or more values of different types. Unlike lists tuple’s length is constant and each tuple is treated as a single value. It is not allowed to change its components or their types. You may think of a tuple as of an argument list of a function.
Consider the following example which builds a tuple of two values (a pair). The first value is an integer while the second is a string.
(123, "String")The next example shows a tuple of three values:
(1, 1, 2.2)The type of a tuple is Cartesian product of the types of its components. For instance, the type of the tuple above is “int * int * double” while of the previous one is “int * string”.
Zip function creates one tuple of the type “int * double” for each pair of elements in the lists fahrenheits / celsiuses and adds it to the resulting list of tuples.
Third, note that a new kind of loop, namely, foreach, is used in this example. Similarly to other kinds of loops foreach is implemented as a macro. The standard implementation provided by the Nemerle macro library is quite flexible so we will not try to create anything near it at this point. Instead of implementing a simpler version (which would be much like the while loop described earlier) we will take a close look at how this loop works.
The syntax of “foreach” looks as follows:
foreach (current_element in collection)
bodywhere “collection” can be any object in Nemerle (and, more generally, in .Net) that could be iterated over. In our case it is the list of tuples that plays the role of such collection. “current element” stands for a variable name which every element in the collection binds to. There we use the pattern (fahrenheit, celsius) which is also new. The pattern decomposes 2-tuples (pairs) onto their elements so that the value of the first element binds to the name fahrenheit while the second element binds to celsius.
This decomposition is yet another illustration of pattern matching in Nemerle even though there is no explicit match operator. However, keep in mind that foreach is a macro so there is a lot of flexibility in how it can process its arguments. For instance, it may generate code involving the match operator and use to match patterns passed as input arguments. This is precisely how foreach works.
Any Nemerle expression, including blocks (expressions in curly brackets), can be used as the loop’s body. The current element is accessible inside the body which is evaluated at every iteration.
Consider the following example:
foreach ((fahrenheit, celsius) in fahrenheits.Zip(celsiuses))
WriteLine("Fahrenheit: {0, 4} Celsius: {1, 5:##0.0}", fahrenheit, celsius);Here the expression
WriteLine("Fahrenheit: {0, 4} Celsius: {1, 5:##0.0}", fahrenheit, celsius);is evaluated for every tuple in the list produced by the expression fahrenheits.Zip(celsiuses). The first element in every tuple is bound to the name fahrenheit while the second goes to celsius.
NOTE
The code above functions as expected since the lists fahrenheits and celsiuses have the same number of elements. Otherwise it would fail due to an exception thrown out of the Zip method. Exceptions will be discussed in later sections.
This is about as far as we can get with the temperature conversion example, so a more advanced use case is needed. One decent possibility is a so called string calculator, i.e., a program that takes a string which encodes an arithmetic expression as an input, parses and evaluates the expression, and finally either prints the result or an error message. For instance, a calculator would output “10” for the expression “5 + 6 – 1” while reporting an error for “10 2” (since an operator is expected instead of 2).
Implementing such calculator will take a few steps each of which will illustrate further features of the language and its standard macro library. The first version will be command line based and it is natural to being with accepting user input.
The following code waits for user input and echoes it back to console:
using System.Console;
def readInput()
{
def result = ReadLine();
unless (result == "")
{
WriteLine("You have entered:");
WriteLine(result);
readInput();
}
}
readInput();There are two unfamiliar things used in this example. The first if the function ReadLine which belongs to the module System.Console. It waits for user input and returns it as soon as Enter has been pressed. The second is the unless operator. Implemented as a macro in the standard macro library it checks the boolean value of the expression passed as the input argument (in our case it is result == "") and, if it is false, it evaluates the expression which immediately follows the closing parenthesis. In the example above that expression is a block.
The implementation of unless is shown below:
macro @unless(cond, body)
syntax ("unless", "(", cond, ")", body)
{
<[ match ($cond) { | false => $body : void | _ => () } ]>
}This must look familiar since the macro simply delegates all the job to the match operator.
So this program invokes the function readInput which reads user input as a string, stores that string in the variable results, checks whether it is empty, and (if not) outputs two other string back to console: “You have entered:” and the entered string. Finally, the function recursively calls itself thus creating an infinite loop. If the user entered the empty string, i.e., pressed Enter without entering a symbol, the function does nothing so the program terminates.
If you compile and run the program, enter, say, “1+1”, and press Enter, the function outputs the following two lines back to console:
You have entered:
1 + 1This can be repeated as many times as you wish. To terminate the program simply press Enter without typing anything.
Currently the program operates with expressions encoded as strings. This is not a suitable representation for evaluating expressions since arithmetic operations can only be performed over numbers (integers or floats). There are two principal ways to sort this out:
1. Parse strings and evaluate the expressions immediately.
2. Transform strings into some intermediate representation that is suitable for subsequent evaluation.
Our task is pretty simple (in contrast to, for example, parsing source code) so we can easily solve it using the first approach. Nevertheless, we will opt for the second since it can perfectly illustrate a generic way of handling complex tasks by decomposing them onto manageable parts. In this case the parts are the following:
1. Splitting each string onto numbers and arithmetic operators while discarding white spaces (spaces, tabs, etc.). On this step, which is known as “lexical analysis”, we can also detect some input errors, for example, presence of unsupported operators or letter. We will call the function performing this kind of analysis lexer.
2. Syntactic analysis (parsing) and expression evaluation.
Lexical analysis involves reading the input string and converting it into a list composed of operators and their operands. As mentioned above, we will also detect some erroneous input, e.g., anything other than numbers and support operators. Currently the calculator supports only four operators: +, -, *, and /.
Lists can only contain elements of a single type while we clearly need to store both operators and numbers. One way to handle this is to reserve some strings to express the operators but this is likely to lead to a highly convoluted and unreadable code. A better option is to use the special user-defined variant type which helps putting elements of different types into a list.
WARNING
If you have a past experience with either VB or COM, be careful not to confuse variant in Nemerle with Variant or VARIANT from VB or COM respectively. There is nothing in common. Nemerle’s variant is more similar to union in C/C++ but, unlike them, it is type safe and can be analyzed in an elegant way via pattern matching.
Variant is an example of a user-defined type. “User-defined” simply means that the type is introduced by a developer for their own purpose. We will use the following variant type Token:
variant Token
{
| Number { value : int; }
| Operator { name : string; }
| Error
}Each instance of Token can store a single value of one of the following types:
- Number,
- Operator,
- Error.
We will use the type Number to store integer values extracted from the input while Operator will store parsed arithmetic operations as strings, i.e., “+”, “-” and so on. Error cannot store anything but is handy to indicate erroneous tokens. Each of the types Number, Operator, and Error is called an option of the variant. Each option’s description begins with “|” followed by the name of the option.
The string shown below:
| Number { value : int; }describes the option for Number. It declares one immutable field value of type int. Each field is a variable stored inside an object of some explicitly specified type. Analogously, the following string:
| Operator { name : string; }describes the option for Operator which has a single field name of the type string. Finally, the line
| Erroris the option for Error having no values at all.
Option’s fields, if any, are enclosed in curly brackets which immediately follow the name. An option can have arbitrary many names. Their order is important since it determines the order of arguments passed into a constructor of the option. Constructors are created automatically based on the option’s description.
Next, consider the function lexer which performs lexical analysis of an input string and returns a value of the type list[Token]. The code is shown below:
def lexer(text : string) : list[Token]
{
mutable index = 0;
def peek() : char
{
if (index >= text.Length) '\0' else text[index]
}
def read() : char
{
def ch = peek();
when (index < text.Length)
index++;
ch
}
def isDigit(ch) { ch >= '0' && ch <= '9' }
def loop(resultTokens : list[Token]) : list[Token]
{
def number(ch : char, accumulator : int = 0) : int
{
def highOrderValue = accumulator * 10;
def currentOrderValue = ch - '0' : int;
def currentValue = highOrderValue + currentOrderValue;
if (isDigit(peek()))
number(read(), currentValue);
else
currentValue
}
def error()
{
WriteLine(string(' ', index - 1) + "^");
WriteLine("A number or an operator expected");
(Token.Error() :: resultTokens).Reverse()
}
def ch = read();
match (ch)
{
| ' ' | '\t' => loop(resultTokens) // skip whitespaces
| '+' | '-' | '*' | '/' => loop(Token.Operator(ch.ToString()) :: resultTokens)
| '\0' => resultTokens.Reverse()
| _ when isDigit(ch) => loop(Token.Number(number(ch)) :: resultTokens)
| _ => error()
}
}
loop([])
}The function deserves a more close attention.
At the beginning, the function defines a mutable variables called index and two auxiliary functions: peek and read:
mutable index = 0;
def peek() : char
{
if (index >= text.Length) '\0' else text[index]
}
def read() : char
{
def ch = peek();
when (index < text.Length)
index++;
ch
}The variable index stores the index of the current symbol in the input string. The index is incremented as the analysis proceeds.
The function peek looks one symbol ahead in the string being analyzed. Note that it is declared inside another function (lexer). This enables peek to access to the arguments of the outer function as well as to variables declared prior to itself. In particular, it uses the argument “text” captured from the outer function. It stores the value of the input string.
Each string in Nemerle is a sequence of characters which are represented using the datatype char. Each character is stored as a number according to the Unicode 16 encoding. Simply put, all characters have their ’’codes’’. Most of them also have a visual representation but some are non-printable and have to be encoded using escape sequences.
Characters are always ordered and a string can have zero or more characters. Strings without characters are called “empty”.
The expression text.Length returns the number of characters in the string that the variable text points to. Don’t worry about Length for the moment, we will get to it later.
“if” is yet another macro based on match operator. Its definition is shown below:
macro @if (cond, e1, e2)
syntax ("if", "(", cond, ")", e1, Optional (";"), "else", e2)
{
<[
match ($cond : bool)
{
| true => $e1
| _ => $e2
}
]>
}As you can see, if the expression cond enclosed in the curly brackets is true then the expression e1, which goes right after the closing bracket, is evaluated and returned as a result of if. Otherwise, the expression that follows else, i.e., e2, is evaluated and returned.
As an example, consider the following expression:
if (index >= text.Length) '\0' else text[index]Its value is ‘\0’ if index is greater than or equal to the length of the string (i.e., when the expression index >= text.Length is true) and is the value of text[index] otherwise.
The string ‘\0’ is an example of a character literal. They describe single characters and are of the type char.
As in string literals, you may use escape sequences in character literals. The sequence ‘\0’ denotes the character having the code 0 (do not confuse it the character 0 whose code is actually 48). This character is also known as the “zero-character”. The same value can be obtained using the type specification: 0 : char.
Consider the following simple illustration of the difference between the character “0” and the zero-character:
using System.Console;
WriteLine('0' : int);
WriteLine('\0' : int);Here is the output:
48
0HINT
All escape sequences which can be used in character literals will be listed in a later section.
As mentioned earlier, characters of a string are ordered in a sequence which, in particular, allows for index-based access to individual symbols. The index of a character is simply its position in the sequence (the first character has the position 0).
The expression text[i] returns the character at the position i in the string that the variable text refers to. For example, the value of the expression text[0] is the first symbol of the string while text[3] returns the fourth character.
WARNING
An index must be a 32-bit non-negative integer. Consequently, strings in Nemerle cannot be longer than 2 147 483 647 characters.
Analogously, the expression text[index] allows for getting a character with the index stored in the variable index.
The function peek does not change the value of index or modify the state of the outer function, so it can be used an arbitrary number of times.
Now, since we covered every single bit of the expression
if (index >= text.Length) '\0' else text[index]And it is time to explain its role in the larger context of the program.
This expression returns either the next character to be analyzed or the zero-character. Checking that the index remains within the the bounds is necessary since otherwise the expression text[index] will throw an exception as soon as the index becomes equal to the length of the string. Throwing and not handling an exception will, of course, abort the program’s execution.
NOTE
Index-based access is a potentially unsafe operation which may, if performed carelessly, cause the program to fail. Unfortunately, it does not take a lot of effort to make a mistake here, so it is usually advisable to minimize explicit use of indexes by taking that logic out into special-purpose functions which keep the indexes under tight control. The program can then be built around those function. This approach, commonly referred to as encapsulation, helps to conceal unsafe or complex details of the algorithm behind simple and understandable abstractions.
In our case the local function read and peek encapsulate the logic of iterating over characters in a string. As soon as the process hits the end of the string (variable text) the functions begin returning the zero-character thus signaling that it is time to stop. That allows the main algorithm to abstract away from such details as controlling the index. All that is important is that the function peek can be used to get the current character being analyzed while the function read will get the next character and move the current position in the string one step forward.
Next, let us have a look at the implementation of read:
def read() : char
{
def ch = peek();
when (index < text.Length)
index++;
ch
}First, the function uses peek to get the next character and stores it in the immutable variable ch. The variable is needed to return the read character at the end of the function.
As you may well guess, when is yet another macro from the standard macro library (it is also based on the match operator). The macro allows for evaluating an expression, e.g., index++ above, if the expression in parentheses, e.g., index < text.Length, is true.
“++” is also a standard macro. It is a unary operator which increments the value of a variable, so index++ is equivalent to index = index + 1.
NOTE
There is also the inverse macro “—” which decrements variables.
Therefore, the expression below:
when (index < text.Length)
index++;increments the value of the variable index and then checks whether it is still less than the length of the string stored in the variable text. Thus, the value of index stops incrementing as soon as it gets out of the bounds.
Since the function read uses peek to read the current character, it also begins returning the zero-character as soon as the end of the string has been reached.
HINT
The current implementation of read based on peek guarantees is the functions will keep the consistent behavior after some other part of the program has been modified. Of course, we could have implemented read differently, i.e., without any use of peek, but our approach helps to avoid potential bugs and increase program’s robustness.
NOTE
The macros “++” and “–-”, as well as the assignment operator, have the return value of the “void” type which precludes their use as sub-expressions. That was done in order to prevent errors which often result from manipulating mutable variables in expressions and to encourage developers to place a tighter control over mutable state. It is the ability to change the state of some part of the program that causes majority of bugs in modern software, so highlighting operations that operate with mutable variables is a step towards alleviating this issue.
The following expression can be used to check if a character is a digit:
ch >= '0' && ch <= '9'Here ch is a variable (or an argument) having the type char while ‘0’ and ‘9’ are literals which correspond to characters “0” and “9”. The expression uses the fact that characters that stand for digits in Unicode follow one another in the natural order (i.e., two characters are arranged in the same relative order as the corresponding digits).
In principle, there is nothing wrong with using the expression above whenever required to check if a character represents a digit. However, it is a little clumsy and, more a way importantly, requires that everyone who happens to read that code understands to the expression is doing. Therefore, it is preferable to take it out into a separate function with clear semantics:
def isDigit(ch) { ch >= '0' && ch <= '9' }Now, wherever this function is used, the intent is immediately clear.
HINT
Nemerle’s standard library provide the global function char.IsDigit which does the same job as our function but in a more correct way. So in production code it is advisable to use that function while our goal was merely to demonstrate how to operate with characters.
“loop” is a function that is responsible for most of the lexical analysis. First, we neglect both its local functions and consider its body at a high level.
def loop(resultTokens : list[Token]) : list[Token]
{
def number(ch : char, accumulator : int = 0) : int { ... }
def error() { ... }
def ch = read();
match (ch)
{
| ' ' | '\t' => loop(resultTokens) // skipping whitespaces
| '+' | '-' | '*' | '/' => loop(Token.Operator(ch.ToString()) :: resultTokens)
| '\0' => resultTokens.Reverse()
| _ when isDigit(ch) => loop(Token.Number(number(ch)) :: resultTokens)
| _ => error()
}
}The function is recursive where each recursive step reads and analyzes the current character in the string.
The argument resultTokens is used to accumulate the result. It stores a list of tokens that have been parsed up to the current point. The function receives the empty list when called by the function lexer for the first time. As it progresses along the string, it adds new tokens to the list.
The next line reads the current character from the input string:
def ch = read();That character is then passed on to the match operator for analysis. If the character is a whitespace (space of tab) then the following expression is executed:
| ' ' | '\t' => loop(resultTokens) // skipping whitespacesNOTE
“\t” is an escape-sequence which represents tabulation.
Whitespaces are simply ignored as they play no role in arithmetic expressions. From the lexical analysis perspective “ignored” means that such characters do not produce any new tokens, so the function loop is called recursively with the same list as on the previous step.
NOTE
Numbers are parsed inside a special function called number which does not skip over whitespaces but rather treats them as syntax errors.
If the current character turns out to be an arithmetic operation (i.e., +, -, *, or /), then the following expression is evaluated:
| '+' | '-' | '*' | '/' => loop(Token.Operator(ch.ToString()) :: resultTokens)It can be broken down into a set of simpler steps. First, the current character is converted into a string using the method ToString:
ch.ToString()“ToString” method is supported by all and every .Net object and produces a string representation of the objects. In the case of a character, the method returns a string which contains that single character. For example, ‘+’.ToString() will return “+”.
The string produced in that way is passed on to the constructor of the option Operator in the variant Token:
Token.Operator(ch.ToString())You may wonder where that argument came from but recall how that option was described earlier:
| Operator { name : string; }A single argument is created for every field of the option so the line:
Token.Operator("+")instantiates the option Operator with the value of name equal to “+”. The instantiated token is placed in the head position of the list resultTokens:
Token.Operator(...) :: resultTokensThe resulting list is next passed on to the next recursive invocation of loop:
loop(Token.Operator(...) :: resultTokens)Let us rewrite the expression to make it more salient. Instead of
loop(Token.Operator(ch.ToString()) :: resultTokens)we may use an equivalent expression which involves a number of intermediate variables with specified types:
def operatorStr : string = ch.ToString();
def operatorToken : Token.Operator = Token.Operator(operatorStr);
def token : Token = operatorToken;
def newRes : list[Token] = token :: resultTokens;
loop(newRes)HINT
The space padding above is used solely to improve readability. The program will compile and run without it but this tabular style makes it easier to read and understand the code.
At this point you should be able to understand all the lines in the example above. The only possible exception is the following:
def token : Token = operatorToken;This only thing going on here is an implicit conversion from the option Token.Operator into the type Token (i.e., into a variant). Variant’s options are compatible with the variant type which defines them. This allows for storing values of the type Token.Operator in the list of the type list[Token]. Furthermore, a single list can contain elements of different options, e.g., Token.Number and Token.Error.
If the current character is ‘\0’, then the following match option is evaluated:
| '\0' => resultTokens.Reverse()As you remember, the zero-character indicates that the end of the input string has been reached. Tokens were always prepended to the head of the list, so the resulting list is reversed. The Reverse method is used to reverse the list back to restore the original order of the tokens. Finally, the list is returned as the result of the function loop.
Note that there is no further recursive call on the last iteration. In other words, the zero-character is an indication to stop the recursion.
If the current character is a digit, then the following option is evaluated:
| _ when isDigit(ch) => loop(Token.Number(number(ch)) :: resultTokens)It calls the local function number which is responsible for parsing numbers. Each parsed number is passed to the constructor of the option Token.Number and the resulting value is added to the beginning of the token list. The list is again passed as the argument of loop.
This match option looks similarly to the one dealing with operators but with two distinctions. First, it uses one unfamiliar syntactic feature of the when… pattern, namely ’’guards’’, and second, the function number deserves a special attention. We will consider the guard first.
Let’s once again consider the following option:
| _ when isDigit(ch) => ...As you already know, the underscore symbol specifies the pattern that matches every expression. However, it is now followed by the construct when isDigit(ch). What does that mean?
Such constructs are called pattern guards. They always begin with the when keyword which is followed by a single Boolean expression (‘’guard condition’’). A guard can be added to any pattern (not necessarily to _) and is used to apply and additional check. In that case the expression is evaluated when first, the pattern is matched and second, the guard condition is true. In our case the condition is the function that checks if the variable ch stores a digit or not:
isDigit(ch)Guard conditions can use any variables or functions visible in the scope where the match is defined as well as all bound variables introduced in the pattern which owns the guard. For example, the option
| _ when isDigit(ch) => ...can be rewritten to
| x when isDigit(x) => ...Here the guard introduces a new variable x which is bound to the expression passed into match as the argument. In our case introducing a new variable probably does not make much sense (since ch has been defined) but it could be useful in some situations. For example, it would have been handy had we directly used the value of the read function in the match operator:
match (read())
{
...
| ch when isDigit(ch) => loop(Token.Number(number(ch)) :: resultTokens)This would allow us to access the value of read via the variable ch (highlighted in the example). In essence, the pattern _ is no more than a special case of variable patterns.
The order of patterns is generally important in match operators (since they are matched in the order they are defined) but it is even more significant for patterns with guards. For example, swapping the patterns
| _ when isDigit(ch) => loop(Token.Number(number(ch)) :: resultTokens)and
| _ => error()the first pattern (which will become the second) will never be matched because the _ will match all values so the guard’s condition will never be evaluated.
The last option of the match operator is the following:
| _ => error()It simply invokes the local function error declared at the end of loop.
def error()
{
WriteLine(string(' ', index - 1) + "^");
WriteLine("a number or an operator expected");
(Token.Error() :: resultTokens).Reverse()
}The role of this function is to output a user-friendly error message which points to the lexically incorrect place. Its first line outputs a string of the form
^where the symbol ^ points to the position in the input string which is considered invalid by the lexical analyzer. The string is created by concatenating the number of spaces equal to error position minus one with the symbol “^”. It is then printed to the console so “^” acts as an arrow which point to the error in the above line (i.e., the input string).
Next, the function prints another line with the message “a number or an operator expected”.
At the end the function prepends an instance of the type Token.Error to the list resultTokens. This lets the next layer of the program, i.e., the syntax analyzer, know that an error has occurred during the lexical analysis. Finally, as when the end of the input string has been reached, the resulting list is reversed and returned as the result of the loop function.
The “number” function shown below parses a part of the string which contains an integer.
def number(ch : char, accumulator : int = 0) : int
{
def highOrderValue = accumulator * 10; // values of higher decades
def currentOrderValue = ch - '0' : int; // value of the current decade
def currentValue = highOrderValue + currentOrderValue;
if (isDigit(peek()))
number(read(), currentValue);
else
currentValue
}The first thing to note is the argument accumulator which has a default value. Such arguments need not be specified when invoking function so if the function is called as follows:
number('1')the value of accumulator will be zero while the following call:
number('1', 5)will set it to 5.
WARNING
Arguments with default values have to be placed at the end of the argument list. They cannot be interleaved with other arguments.
All operators used in this function should look familiar but we will nonetheless take into pieces. The first three lines:
def highOrderValue = accumulator * 10;
def currentOrderValue = ch - '0' : int;
def currentValue = highOrderValue + currentOrderValue;calculate the current value of the number being parsed. The number can have several decades (each of which is character) so the parsing is performed via recursion on the length of the string.
The accumulator argument contains the value of the number computed on the previous recursive step (or 0, if it is the first invocation). Multiplying that value by 10 gives us the value of the higher decades of the number:
def highOrderValue = accumulator * 10;The current decade’s value can be obtained from the code of the current character (the one stored in the variable ch) simply by subtracting the code of ‘0’:
def currentOrderValue = ch - '0' : int;As it is said earlier, numerical codes for the characters representing digits go in an ascending order such that each next code is equal to the previous plus one. Therefore, subtracting the code of ‘0’ from the code of any digit X results in the value of X. For example, the result of
'2' - '0' : intis simply “2”. The type specification is necessary here since the subtraction operator is undefined for chars so the values need to be converted into int. This is precisely what happens when the type int is specified for any of the operands. The compiler can then infer the type for the second operand so the operation is carried out over integers.
The next step is to add the value of the current decades to the accumulated higher decades:
def currentValue = highOrderValue + currentOrderValue;Now the variable currentValue stores the value of parsed part of the number.
Let’s consider a simple example illustrating the process. Assume that the number function is being used to parse the number of 12. On the first recursive step the value of accumulator is zero while the argument ch is equal to ‘1’. Multiplying accumulator by 10 still gives zero (in the code below the argument accumulator is replaced by its current value):
def highOrderValue = 0 * 10;As you can see the variable highOrderValue is going to contain zero.
The current value of ch is ‘1’. We then subtract the code of ‘0’ from it
def currentOrderValue = '1' - '0' : int;and result, i.e., “1”, is stored in the variable currentOrderValue. Adding 0 to 1 is 1 which is stored in the variable currentValue:
def currentValue = highOrderValue + currentOrderValue;The next step is to heck if the next character is a digit or not:
if (isDigit(peek()))In our example the next character is ‘2’ so the condition, i.e., the return value of isDigit, is true. This leads to the recursive call of the number function whose arguments are now ‘2’ (ch) and 1 (accumulator):
number('2', 1) // arguments are replaced by their respective valuesThe function again performance the same sort of calculations:
def highOrderValue = accumulator * 10;
def currentOrderValue = ch - '0' : int;
def currentValue = highOrderValue + currentOrderValue;Now the value of accumulator is 1 and the result of ch – ‘0’ : int is 2, so the resulting value of currentValue is 12. The next character of the input string is not a digit and the isDigit function returns false. Therefore the function is going to stop the sequence of recursive calls and return the value of 12.
WARNING
The function number is auxiliary meaning that its usage makes sense only in the context of another function, e.g., loop. It is called only if the main analysis function, loop, determines that the current character is a digit. At this point the character is stored in the argument ch. There is no other way how number can know the value of the current character since loop reads characters using the read function, so a possible call to peek would return the character next to the current. The function number does not check the value of ch assuming that it cannot be invalid. Such assumptions are acceptable only when it is known in advance that the arguments will be valid for all future invocations. Later you will learn how to represent such assumptions explicitly but for now it is best to keep in mind that they are potentially unsafe, should be carefully checked or, ideally, avoided at all. For example, passing any character other than a digit as the value of ch would cause number to function incorrectly.