CUDA

The GPU Computation framework.

This is an excerpt from our final year project report, titled "Fractional Calculus using CUDA". The team members include
Guides: Bhavana B Turorikar, Dr.Vishwesh Vyawahare

1. Somesh Musunuri (the most versatile coder).
2. Naveen Peddyreddy (the mathe-magician).
3. Ameya Mhatre (the LaTex & Matlab genius)
4. Avinash Maurya (Me :D)

Introduction

This project was focused on developing libraries in NVidia's CUDA framework for some Special functions in Calculus, specifically Fractional Calculus. We'll break it down a bit for ease of explanation:

• Normally calculus deals with derivatives like dy/dx, d²y/dx², d³y/dx³... i.e in Integral order. Similar goes for Integrations.
• Integral calculus is a special case of Fractional calculus, which deals in fractional order Derivatives and Integrations. Eg. d^1.2y/dx^1.2 or something like 4.3! (4.3 Factorial)
• Some special functions in fractional calculus are computationally very expensive, i.e require a lot of iterative calculuations eg. Caputo Fractional, Mittag-Leffler and others. This is where CUDA comes in.
• CUDA is a framework developed by NVidia to harness the multi-core architecture of GPU(Graphics Processing Unit) for General Purpose computing.

---

Motivation

Most of the programming languages, frameworks or tools which exist today are CPU based, i.e. the CPU is responsible for processing the program and giving outputs. With the growing need of more compute power, we are building more cores in our CPUs or over-clocking it to gain a better throughput. An alternative approach for the CPU problem is General Purpose Graphic Processing Unit (GPGPU) computing. Since the last decade, the semiconductor industry is exploring ways to harness the compute ability of GPU for General Computing purposes. This shift in paradigm of GPU from rendering video and display parameters to General purpose computing has opened new opportunities for enhanced compute performance of commodity computers.

---

The making

Finding the Right implementation is the Tough part

Enters our Mathe-Magican, Naveen
Let's start with the most basic, the Gamma function (Γ)
Traditionally, the formula for computing Gamma value is:

Approach One:

The above formula can be used for parallel implementation, we can launch multiple threads with different values of x with an increment index of 0.001, so the equation would roughly tanslate to:

1. Γ(z=4) = 0^(4-1)*e^-0 + 0.001^(4-1)*e^-0.001 + 0.002^(4-1)*e^-0.002 + 0.003^(4-1)*e^-0.003 + ...

Here we could take up each term and compute it on a different thread, finally then recursively add the results of each thread (algorithmically in O(logN) complexity).

Approach Two:

Use the Weierstrass's definition for approximation of Gamma function.

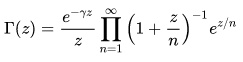
here, γ = 0.57721

This equation was better suited for our needs because it was computationally a bit less expensive(x^(z-1) would be heavier as compared to (n/(n+z))), it was the recommended parallelised approach and it gave us a better programmatic-understanding if the increments were integral.

Implementation is a Tougher part

Here come the duo Matlab genius-Ameya & Versatile Coder-Somesh
Now that we figured out what we need to make, we need to translate it algorithmically. We made the codes for the same Weierstrass's implementation in Matlab first, tested it out for several values and checked its computation-time, first without vectorization and then with vectorization on GPU. Matlab abstracts the sharing of jobs to thread, there's no fine control over allocation of blocks and threads. So we just used it as a tool to check the correctness of values.
The load of translating the mathematical equations to programs was done using matlab first, results were verified and then we proceeded with its C++ implementation. Our intention was to check the speedup time achieved using a parellised architecture vs a CPU based single-core implementation.
We ran many different permutaions of block-size, thread-size, reduction techniques and other intricate details to achieve a high throughput.

We used IIT-B's GCOE for implementation of this project:
Configuration:
GPU: Tesla K40 - 2880 cores
CPU: Intel(R) Xeon(R) CPU E5-2620@ 2.00GHz with 24 cores.

More on Implementation & debugging coming soon... We'd be writing a series of posts about the core implementation details and the workflow...

Result is the Sweet part

So with all that handled, we got a great speedup for our algorithm as under:

Gamma	Time taken for C++	Time taken for CUDA	Net Speed up
z=4.2	135.7	0.46	291
z=5.2	137.1	0.44	309.8
z=6.0	137.7	0.44	310.4