-
Notifications
You must be signed in to change notification settings - Fork 15
Tutorial ParabolicDish V201
This tutorial explains how to use Tonatiuh release 2.0.1 to model a parabolic dish and simulate its optical behaviour. It also explains how to use Mathematica to process the output from Tonatiuh to estimate the concentrated solar flux distribution at the focal plane of the parabolic dish and related parameters, such as the maximum radius of such distribution, i.e., the size of the solar radiation spot at the focal plane.
The parabolic dish we are going to model is composed of a parabolic dish mirror and a flat disk receiver located in the focal plane of the mirror and centred at the focal point.
For simplicity, we are going to assume that the mirror is a perfect specular mirror of ideal paraboloidal shape and the receiver is a perfect absorber of ideal flat disk shape.
We are going to use the following values for the parameters defining the geometry of dish and the receiver:
- Parabolic mirror * Radius = 5 meters * Focal length = 6.0454798 meters
- Flat disk receiver * Radius = 0.06 meters
Such a parabolic dish, which has an f-Number (ratio of the focal length to the dish diameter) of 0.60454798, achieves the maximum geometric concentration ratio for a parabolic dish.
After starting Tonatiuh release 2.0.1, do the following:
- Add a Group Node to the RootNode and label it "ConcentratingSystem".
- Add a Group Node to the "ConcentratingSystem" Group Node and label it "ParabolicDish".
- Add a second Group Node to the "ConcentratingSystem" Group Node and label it "!Receiver".
After doing this, Tonatiuh's user interface should look like this:
The 3D pane view located to the left of Tonatiuh's Graphics User Interface (GUI) does not show any surfaces, since we have not defined them yet. The Symbolic pane view located to the right of Tonatiuh's GUI shows the Group Node tree structure we have just created. In this tree structure, the Group Nodes represent three-dimensional reference frames. Each one of these reference frames can be translated and rotated with respect to the reference frame of their parents. The dimensions along the axes of each reference frame can be independently scaled. By default Tonatiuh creates the Group Note with the x-z plane as the horizontal plane and with the y-axis as the vertical axis, positive upwards. Since we have not changed the default parameters, the three reference frames created with the three Group Nodes just defined ("ConcentratingSystem", "ParabolicDish", "Receiver") are all coincident with the world reference frame represented by the Group Node "RootNode".
- Click on the "ParabolicDish" Group Node to select it. Add to it a Surface Node and keep the automatic label "!TShapeKit1" provided by Tonatiuh.
- Click on the just created "TShapeKit1" Surface Node and add to it: * A "Parabolic_Dish" node. * A "Specular_Standard_Material" node.
After doing this, if you select within the "View" menu the option "Edit Mode" and set up the four 3D-Windows of the 3D pane view appropriately, Tonatiuh's user interface should look like this:
As Tonatiuh's GUI shows, we have managed to create a parabolic dish. However, the parabolic dish that we have created is not the parabolic dish we wanted to model. The reason for this is that we have not changed the default values that Tonatiuh assigns to any newly created parabolic dish. This default values are:
- A focal length "focusLength" of 0.125 meters.
- A minimum radius "dishMinRadius" of 0.1 meters.
- A maximum radius "dishMaxRadius" of 0.5 meters.
- A maximum rotational angle "phiMax" of 2 Pi.
- An active side for representation purposes "activeSide" of "OUTSIDE".
Obviously, we have to change the values assigned to some of the above listed variables to model the parabolic dish we are interested in. The changes that we need to carry out are the following:
- Change the focal length "focusLength" to 6.0454798 meters.
- Change the minimum radius "dishMinRadius" to 0. meters.
- Change the maximum radius "dishMaxRadius" to 5 meters.
- Change the active side for representation purposes "activeSide" to "INSIDE".
After doing this, Tonatiuh's user interface should look like this:
Although, we have modelled the geometry of the parabolic dish, we still have to model its physical properties. To do this, we select the "Specular_Standard_Material" node and change the values of the following variables from their default values to the following ones:
- m_reflectivity = 1 (default value 0)
- m_sigmaSlope = 0 (default value 2)
By setting the reflectivity to 1 and the sigma slope to 0 we are telling Tonatiuh that the mirror should be modelled as an ideal specular reflective mirror that follows exactly Descarte's law of reflection.
- Click on the "Receiver" Group Node to select it and change the value of the translation variable from "0 0 0" to "0 6.0454798 0" in order to translate the flat disk's reference frame in the vertical y-direction and place its origin at the focal point of the mirror.
- Add to the "Receiver" Group Node a Surface Node and keep the automatic label "TShapeKit1" provided by Tonatiuh.
- Click on the just created "TShapeKit1" Surface Node and add to it: * A "Flat_Disk" node. * A "Specular_Standard_Material" node.
- Select the "Flat_Disk" node and change the "radius" from 0.5 meters (default) to 0.06 meters, and the "activeSide" from "FRONT" to "BACK".
After doing this, if you select within the "View" menu the option "Edit Mode" and set up the four 3D-Windows of the 3D pane view appropriately, Tonatiuh's user interface should look like this:
- From Tonatiuh's menu bar select "Environment>Sun Light>Define SunLight" in order to make the program to display the "Define SunLight" dialog.
- In the "Sun Shape" tab of that dialogue, select "Pillbox_Sunshape" as the "Sunshape Type".
- Accept the default values provided by the program for the direct solar irradiance (1000 W/m2) and for the maximums half angle subtended by the direct solar radiation, "thetaMax" (0.00465 radians or 16 minutes of arc) and click "OK".
We do not need to change the azimuth and elevation of the sun vector, because by default the azimuth is considered 0 degrees and the elevation 90 degrees, that is, the sun vector, by default, is defined in the y-direction pointing upwards and, therefore, aligned with the optical axis of the parabolic mirror we just modelled.
Once we have modelled the solar concentrating system and the incoming direct solar radiation, we are ready to run Tonatiuh in order to ray trace rays from the Sun into the concentrating system and collect the ray traced rays for post processing outside Tonatiuh.
To specify how many rays we want to generate, and other ray tracing options we go to the main menu bar and select "Ray Trace>Ray Trace Options" in order to make the program to display the "Ray Trace Options" pop up dialog, shown in the Figure below.
In this dialogue let us just modify the number of rays to be traced by Tonatiuh from the default value of 10000 to 75 million rays, and click the "OK" button.
Once this is done, let us run the ray tracer by selecting on the main menu the option "Ray trace>run". This will trigger the display by Tonatiuh of the "Photon Map Export Settings" dialogue.
In this dialogue, change the values of the following options from their default values to the ones indicated below:
- Store type = Binary_file
- Directory name = The directory where you want to store the results
- File name = Receiver
- Select photons to store = Export surfaces
- Select photons information to store:
- Coordinates
- Local Coordinates
- Surface identifier = No (unselected)
Since we have selected "Export surfaces" as the option of "Select photons to store" we need to specify which surfaces we are interested in. In our case, we are just interested in exporting the photons incident upon the flat disk receiver. Thus, we need to add that surface to the list of "Export surfaces". We do this by clicking on the "Add" button and selecting the appropriate surface in the "Select Surface Dialog" that will pop up. Actually, what we need to select is the "TShapeKit1" node that is the parent of the "Flat_disk" surface.
Once we have finished selecting and entering the appropriate values in the "Photon Map Export Settings" dialog, the content of such dialog should look like the Figure below:
Now, to run the program we just need to click on the "OK" button of the "Photon Map Export Settings" dialog. How much time Tonatiuh will need to trace the 75 million rays depends on the characteristics of the computer in which we are running Tonatiuh. In principle, Tonatiuh should be able to detect the number of cores you have on your computer system and parallelize the ray tracing accordingly. When carrying out the ray tracing, Tonatiuh will display a dialog informing the user of the number threads it is using and degree of completion of the ray tracing activity, as shown in the Figure below.
In the computer I used to develop this tutorial (a Dell laptop with an Intel Core i5.3360M at 2.8 GHz and 4 GB of RAM, running a 32/bit Windows 7 Enterprise operating system) it took Tonatiuh around 4 minutes to trace the 75 million rays and store the related information on disk.
After carrying out the ray tracing of the 75 million rays, Tonatiuh stored the information about the photons that it has traced in a series of binary files. Since we established as the core name of the files "Receiver", Tonatiuh generated 58 files, starting in the file "Receiver_1.dat" and ending in the file "Receiver_58.dat". As we established when selecting the options for the ray tracing, all of these files, but the last one, contain information about 10 million photons.
In addition to the 58 binary data files, with information about the different photons incident on the flat disk receiver, Tonatiuh also generated a file entitled "Receiver_parameter.txt" with the following content:
START PARAMETERS
id
x
y
z
side
END PARAMETERS
START SURFACES
1 //SunNode/RootNode/ConcentratingSystem/Receiver/TShapeKit1
END SURFACES
0.00137342
The above information is essential to process the binary data files correctly.
- The information contained within the "START PARAMETERS" and "END PARAMETERS" labels, specify how the photon information on the binary data files is structured.
- The information contained within the "START SURFACES" and "END SURFACES" labels, specify the path of each of the ShapeKits associated with the surfaces we exported. In our case, we just exported one surface -the flat disk receiver. In fact, saying that we exported a surface is a lose way of talking. What we actually exported are the photons impinging on either side of the surface.
- Finally, the real number at the end of the file, just after the "END SURFACES" label, indicates the power per photon in Watts, to be considered when estimating concentrated solar fluxes and power values.
According to the information provided in the "Receiver_parameter.txt" file, the 58 binary data files contains of the order of 10 million of 5-tuples, with each 5-tuple providing the following information about a photon impinging on the disk flat receiver:
- The photon id.
- The x-coordinate of the photon.
- The y-coordinate of the photon.
- The z-coordinate of the photon.
- The side of the surface in which the photon is impinging (0 if is in the back side, and 1 if is in the front side)
Since we selected "Local Coordinates" in the "Photon Map Export Settings" before ray tracing with Tonatiuh, the x, y, and z coordinates of the photons are given in the local coordinate reference frame of the flat disk receiver. In this reference frame, the flat disk receiver is located on the x - z plane with its "FRONT" side looking upwards in the direction of the positive y-coordinates. The centre of the flat disk receiver is located at the origin of the local reference frame. Since the photons are impinging on the flat disk receiver and this is located in the x-z plane of the local reference system, the y-coordinates of all the impinging photons should be zero. Due to numerical errors, it may be the case that these coordinates are not exactly zero. However, if they are not exactly zero, they should be extremely close to zero.
To process Tonatiuh's results binary data files with Mathematica the first thing we need to do is to specify Mathematica the directory where the data files are located.
One way to do this is to set up the working directory of our Mathematica notebook file as the directory where Tonatiuh's binary data files are located, and one way to do this is to locate our Mathematica notebook in that directory, and instruct Mathematica to consider as its working directory the directory where the notebook is located. This is done, with the following instruction:
SetDirectory[NotebookDirectory[]]Defining an auxiliary function to determine if a photon is impinging in the correct side of the receiver flat disk
Because of the geometry of the concentrating system we are simulating and the relative position of the Sun with respect to it, it is evident that a small portion of the photons from the Sun will directly hit the flat disk receiver in its front surface, while the majority of the photons will first hit the parabolic dish mirror and after being reflected in it will hit the back surface of the flat disk receiver.
Since we are interested in estimating the solar flux distribution in the side of the flat disk receiver that is facing the parabolic dish mirror, we need to differentiate the photons that are impinging on the front surface of the flat disk receiver from those which are impinging on the back surface of the receiver. To do this, we just need to check the value of the sideID in the 5-tuple set of data providing the information of a given photon.
To facilitate the filtering of the photons that are impinging on the wrong side of the receiver flat disk we define in Mathematica a trivial function that gets as an input the 5-tuple of a photon and the reference ID of the receiver side, refDide (1 = FRONT, 0 = BACK) and return True if the photon is in the correct side of the receiver and False otherwise. This function is defined as follows:
side[{photonID_, x_, y_, z_, sideID_}, refSide_] := sideID == refSideSince we told Tonatiuh to use as the "core" of the binary data files filenames "Receiver", we can get the complete list of binary data files to be processed with the following Mathematica statement:
In[5]:= file = FileNames["Receiver_*.dat"]
Out[5]= {"Receiver_10.dat", "Receiver_11.dat", "Receiver_12.dat", \
"Receiver_13.dat", "Receiver_14.dat", "Receiver_15.dat", \
"Receiver_16.dat", "Receiver_17.dat", "Receiver_18.dat", \
"Receiver_19.dat", "Receiver_1.dat", "Receiver_20.dat", \
"Receiver_21.dat", "Receiver_22.dat", "Receiver_23.dat", \
"Receiver_24.dat", "Receiver_25.dat", "Receiver_26.dat", \
"Receiver_27.dat", "Receiver_28.dat", "Receiver_29.dat", \
"Receiver_2.dat", "Receiver_30.dat", "Receiver_31.dat", \
"Receiver_32.dat", "Receiver_33.dat", "Receiver_34.dat", \
"Receiver_35.dat", "Receiver_36.dat", "Receiver_37.dat", \
"Receiver_38.dat", "Receiver_39.dat", "Receiver_3.dat", \
"Receiver_40.dat", "Receiver_41.dat", "Receiver_42.dat", \
"Receiver_43.dat", "Receiver_44.dat", "Receiver_45.dat", \
"Receiver_46.dat", "Receiver_47.dat", "Receiver_48.dat", \
"Receiver_49.dat", "Receiver_4.dat", "Receiver_50.dat", \
"Receiver_51.dat", "Receiver_52.dat", "Receiver_53.dat", \
"Receiver_54.dat", "Receiver_55.dat", "Receiver_56.dat", \
"Receiver_57.dat", "Receiver_58.dat", "Receiver_5.dat", \
"Receiver_6.dat", "Receiver_7.dat", "Receiver_8.dat", \
"Receiver_9.dat"}To estimate the flux in the back surface of the receiver flat disk the following variables must be defined and initialized:
"Initialization of variables"
"Number of Tonatiuh's binary data files to be processed"
numberOfFiles = Length[file]
<i>58</i>
"Radius of the flat disk receiver"
rReceiver = 0.06 (* m *)
<i>0.06</i>
"Power per photon as indicated in Tonatiuh's output file "Receiver_parameters.txt""
In[64]:= powerPerPhoton = 0.00137342 (* W/m2 *)
Out[64]= 0.00137342
"Number of elements in which we want to divide each side of the circumscribing square about the disk receiver"
In[65]:= nElements = 100
Out[65]= 100
"Length of the sides of the elements in which we are dividing the circumscribing square about the disk receiver"
In[66]:= ds = (2 rReceiver)/nElements (* m *)
Out[66]= 0.0012
"Area of the square elements in which we are dividing the circumscribing square about the disk receiver"
In[67]:= elementArea = ds * ds (* m^2 *)
Out[67]= 1.44*10^-6
"Array of nElements by nElements with all the elements initialized to zero"
In[68]:= totalPhotonsCounts = ConstantArray[0, {nElements, nElements}];
"Total number of photons reaching the back side of the flat disk receiver"
In[69]:= totalNumberOfPhotons = 0
Out[69]= 0
"Radius in meters of the minimum circle that contains all photons impinging on the back side of the receiver"
In[70]:= rMin = 0.
Out[70]= 0.
"Factor to convert number of photons within a given element of area into solar flux intensity"
In[71]:= conversionFactor = powerPerPhoton/(elementArea*1000000) (* MW/m2 *)
Out[71]= 0.000953764Once the above variables have been properly defined and initialized, we are ready to process all Tonatiuh's results binary data files in order to estimate:
- The flux distribution at the back side of the flat disk receiver,
- The minimum radius of the circle that contains all of the photons impinging on the back side of the receiver, i.e. the radius of the spot of concentrating sunlight on the receiver.
- The total power incident on the back side of the receiver.
The Mathematica code to carry out the processing of the binary data files is the following:
For[i = 1, i <= numberOfFiles, ++i,
fileRawData = BinaryReadList[file[[i]], "Real64", ByteOrdering -> +1];
filePhotonSet =
Partition[fileRawData[[1 ;; Length[fileRawData]]], 5];
Clear[fileRawData];
fileValidPhoton =
Select[filePhotonSet,
side[#, 0] &] /. {photonID_, x_, y_, z_, sideID_} -> {x, z} ;
Clear[filePhotonSet];
rMin = Max[rMin, Sqrt[Max[fileValidPhoton /. {x_, z_} -> x*x + z*z]]];
Print["Iteration # ", i, ". Processing file: ", file[[i]], " rMin= ",
rMin, " "];
fileNumberOfValidPhotons = Length[fileValidPhoton];
totalNumberOfPhotons =
totalNumberOfPhotons + fileNumberOfValidPhotons;
filePhotonCounts =
BinCounts[
fileValidPhoton, {-rReceiver, rReceiver, ds}, {-rReceiver,
rReceiver, ds}]; Clear[fileValidPhoton];
totalPhotonsCounts = totalPhotonsCounts + filePhotonCounts;
Clear[filePhotonCounts]]The For loop runs from i = 1 to i = numberOfFiles, which ensures the processing of all binary data files output by Tonatiuh. For every binary data file, the first thing that is done is to read the file as a list of long double numbers ("Real64") and storing the list of double numbers in the variable named "fileRawData". This is done by the following Mathematica statement:
fileRawData = BinaryReadList[file[[i]], "Real64", ByteOrdering -> +1];By providing the option ByteOrdering -> +1 we are assuming that the ordering of the bytes in the binary representation of the numbers follow the "big endian" convention.
Once we got the raw list of long double numbers stored in the data file, the next step is to structure that raw list of numbers into 5-tuples, since we know that for every photon Tonatiuh is providing in the binary file the PhotonID, the three (x, y, z) local coordinates, and the SideID, indicating if the photon is impinging on the front or on the back of the surface. This is done by the following Mathematica statement. which stores the newly created structured list of 5-tuples in the variable named "filePhotonSet":
filePhotonSet = Partition[fileRawData[[1 ;; Length[fileRawData]]], 5];Once we have partitioned into 5-tuples the initial list of long doubles stored in the "fileRawData" variable and stored it in the variable "filePhotonSet", we no longer need the raw list stored in "fileRawData". Thus, in order to save memory we erase the content of "fileRawData" using the following Mathematica statement:
Clear[fileRawData];Now, from the 5-tuples associated to the photons impinging on any side of the flat disk receiver we need to select only those that are impinging on the back of the receiver, which is the side of the receiver looking towards the parabolic dish mirror and receiving the concentrated solar radiation reflected by it. Furthermore, from those valid photons, we just need to know their (x,z) coordinates, since their y-coordinate, which is the coordinate in the normal direction to the plane of the flat disk must be zero. The selection of the appropriate photons and the transformation of the 5-tuples in 2-tuples or pair of (x, z) coordinates is achieved by the following Mathematica statement, which stores the pairs of (x,z) coordinates of the valid photons on the variable named "fileValidPhoton":
fileValidPhoton =
Select[filePhotonSet,
side[#, 0] &] /. {photonID_, x_, y_, z_, sideID_} -> {x, z} ;As before, since the content of "filePhotonSet" is not longer needed, we erase the variable using the Clear[filePhotonSet] Mathematica statement.
Once we have the (x,z) coordinates of all the photons contained in the binary file that we are processing, we calculate the distance of each photon from the centre of the disk, obtain the greatest distance of them all, and update rMin accordingly (i.e., if the distance stored in rMin is smaller than the largest distance we have encountered processing the file, we replace rMin with the new largest distance. However, if that is not the case, we keep the original value of rMin). This updating of rMin is achieved by the following Mathematica statement:
rMin = Max[rMin, Sqrt[Max[fileValidPhoton /. {x_, z_} -> x*x + z*z]]];Since, the processing of all the binary data files may take long, to provide some feedback to the user, for every file processed in the loop we print the loop iteration number, the name of the file, and the value of rMin. This is done by the following Mathematica statement:
Print["Iteration # ", i, ". Processing file: ", file[[i]], " rMin= ",
rMin, " "];Then, we update the variable totalNumberOfPhotons adding to it the number of valid photons contained in the binary file being processed. This is done by the following Mathematica statement:
totalNumberOfPhotons = totalNumberOfPhotons + Length[fileValidPhoton];Finally, we update the (nElements x nElements) array named "totalPhotonsCounts" containing the number of photons per element of area with the additional number of photons per element or area obtained from processing the current binary file. This updating is achieved by the following Mathematica statement, which represents a matrix or array addition:
totalPhotonsCounts =
totalPhotonsCounts +
BinCounts[
fileValidPhoton, {-rReceiver, rReceiver, ds}, {-rReceiver,
rReceiver, ds}];Once this is done, we erase the content of the fileValidPhoton variable to save memory, using the Clear[fileValidPhoton] statement, and go back to the beginning of the For loop to process a new Tonatiuh binary data output file.
At the exit of the binary data files processing loop:
- The "totalNumberOfPhotons" variable stores the total number of photons that impinged on the back side of the flat disk receiver out of the 75 millions traced by Tonatiuh.
- The "totalPhotonCoutns" 100 x 100 array stores in each of its elements the number of photons which impinged in the corresponding area elements of the circumscribing square about the disk receiver.
- The "rMin" variable stores the maximum distance from the centre of the flat disk receiver of any of the photons impinging on the back side of the receiver, which is the minimum radius of the circle around the centre of the receiver that enclosed all the incoming photons.
The power at the receiver is estimated by multiplying the total number of photons reaching the back side of the receiver by the total power per photon. This is done with the following Mathematica statement:
In[18]:= estimatedPowerAtReceiver =
powerPerPhoton totalNumberOfPhotons/1000 (* kW *)
Out[18]= 78.5262The division by 1000 is used to provide the figure in kilo Watts rather than in Watts.
The flux distribution at the receiver is estimated by multiplying by the value stored in the variable "conversionFactor" each one of the elements of the array containing the number of photons impinging upon the corresponding elements of area in which we have divided the circumscribing square about the flat disk receiver. This is done with the following Mathematica statement:
fluxDistribution = conversionFactor * totalPhotonsCounts;This flux can be graphically represented in Mathematica in many forms,such as a ListContourPLot or ListPlot3D.
To represent the flux as a ListCountourPlot we can use the following Mathematica statement:
ListContourPlot[fluxDistribution, Contours -> 10,
DataRange -> {{-0.06, 0.06}, {-0.06, 0.06}}]The graph generated by Mathematica as a result of executing the previous statement is the following:
To represent the flux as a ListPlot3D we can use the following Mathematica statement:
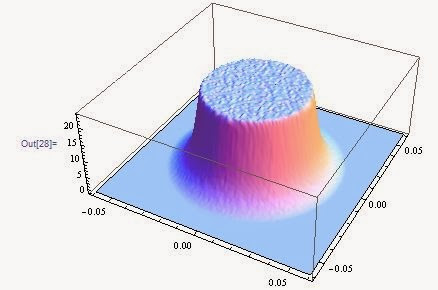
ListPlot3D[fluxDistribution, InterpolationOrder -> 1, Mesh -> None,
DataRange -> {{-0.06, 0.06}, {-0.06, 0.06}}]The graph generated by Mathematica as a result of executing the previous statement is the following:
This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 Unported License