-
Notifications
You must be signed in to change notification settings - Fork 36
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
curve.f90:evaluate_curve_barycentric() broken when num_nodes exceeds 30
#156
Comments
|
@saxenarohan97 Thanks for stopping by, it's great to hear from users! Sorry for my 12 day (:scream:) delay here (advent of code has been stealing all my free time).
So, the
You should just use
I have observed this as well (see notebook), even in a case where I use degree elevation (which should only change the nodes, not the curve itself) and degree 29 (i.e. 30 nodes) plot becomes Thanks for surfacing this bug, hopefully something comes of it! (I have marked the issue as |
|
So, one preliminary finding is that the It does this by isolating the pure-Python components (from the Fortran speedup binary extension) import bezier._curve_helpers
def _bezier_evaluate_multi_py(nodes, s_vals):
one_less = 1.0 - s_vals
return bezier._curve_helpers._evaluate_multi_barycentric(
nodes, one_less, s_vals
)Another side note: The reason this "worked" with a mismatch of degree and the number of nodes is that |
|
Regarding INTERPOLATION, you can do this with a little bit of math by using an "elevation matrix" starting from the identity matrix. For example, to produce the matrix in the via >>> import bezier
>>> import numpy as np
>>> degree3_identity = bezier.Curve.from_nodes(np.eye(3, order="F"))
>>> degree3_elevated = degree3_identity.elevate()
>>> degree3_elevated.nodes * 3
array([[3., 1., 0., 0.],
[0., 2., 2., 0.],
[0., 0., 1., 3.]])We can extend this to elevating multiple degrees, e.g. from degree 3 (4 nodes) to degree 30 (31 nodes): >>> curve = bezier.Curve.from_nodes(np.eye(4, order="F"))
>>> for _ in range(31 - 4):
... curve = curve.elevate()
...
>>> curve.degree
30
>>> elevation_matrix = curve.nodes
>>> elevation_matrix.shape
(4, 31)This "elevation matrix" This is great if we know which translates to >>> interpolation_matrix = np.linalg.solve(
... elevation_matrix.dot(elevation_matrix.T),
... elevation_matrix,
... ).TDoing this to our "broken" curve of degree 30 (31 nodes) from the gist produces a cubic that "looks right": NOTE: When computing the elevation matrix, each intermediate stage can be computed exactly as rational numbers, so for some applications it may make sense to avoid roundoff as long as possible. This can be done with something like |
num_nodes exceeds 30
|
Hi @dhermes. Thanks a lot for your reply and detailed investigation of the issue. I too must apologize for my late response! I suppose the main takeaway for users from your comment is that calling However, if I replace from bezier import Curve
import numpy as np
def create_curve(npoints):
x = sorted(np.random.randint(1000, size=npoints).astype('float'))
y = sorted(np.random.randint(1000, size=npoints).astype('float'))
nodes = np.asfortranarray([x, y])
curve = Curve.from_nodes(nodes)
curve.plot(num_pts=100)Am I still messing up something? :( |
|
Thanks for coming by @saxenarohan97.
I fixed the issue, but have not released the fix yet. You are doing nothing wrong, thanks for checking! I hope to make the
Not necessarily, but rather that you should use the constructor with the correct degree. (But your accidental mis-usage of the constructor was great because it contributed the |
|
@saxenarohan97 OK version |






I want to use the module for fitting a curve through more than 30 points. However, I found that the interpolation "breaks" for >30 points. Minimal reproducible example:
Note that the points I've passed to
bezier.Curveare monotonically increasing, so the resulting approximation curve should also be monotonically increasing.If I fit a curve through 30 points, then it works as expected:
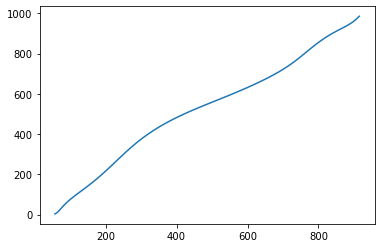
>>> create_curve(30)However, if I use >30 points:
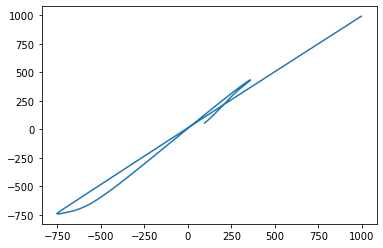
>>> create_curve(31)Then the curve loops in on itself - which it shouldn't - since all points are positive and monotonically increasing.
Any idea what might be the issue (or if there is a problem with my example code)?
The text was updated successfully, but these errors were encountered: