This is a collection of functions implemented in python that replicate their implementation in GrADS.
Requires Numpy for the calculations. We use Xarray to read in the nc files, Matplotlib and Cartopy for plotting. Below there is a simple example to be ran with the sample data included in the package.
pip install mygrads
import mygrads as mgimport numpy as np
import xarray as xr
import cartopy.crs as ccrs
import matplotlib.pyplot as plt# We are using some sample data downloaded from the NCEP Reanalysis 2
# Downloaded from: https://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis2.html
# Zonal wind
ds = xr.open_dataset('data/u.nc')
u = ds['uwnd'][0,0,:,:].values
lat = ds['lat'].values
lon = ds['lon'].values
# Meridional wind
ds = xr.open_dataset('data/v.nc')
v = ds['vwnd'][0,0,:,:].values
# Temperature
ds = xr.open_dataset('data/t.nc')
t = ds['air'][0,0,:,:].valuesIdentical as GrADS hdivg (ref.).
div = mg.hdivg(u,v,lat,lon)Or the vertical component of the relative vorticity. Identical as GrADS hcurl (ref.)
vort = mg.hcurl(u,v,lat,lon)This is not natively implemented in GrADS. Nonthenless, it is pretty straightforward given the above functions, and already described here.
tadv = mg.hadv(u,v,t,lat,lon)This replicates the cdiff function of GrADS (see their docu. "The difference is done in the grid space, and no adjustment is performed for unequally spaced grids. The result value at each grid point is the value at the grid point plus one minus the value at the grid point minus one."
It is also used internally here in hdivg, hcurl and hadv implementatinos. The numpy-like argument axis should be 0 or 1, to indicate the dimension over which the derivative is being calculated.
latv, lonv = np.meshgrid(lat, lon, indexing='ij')
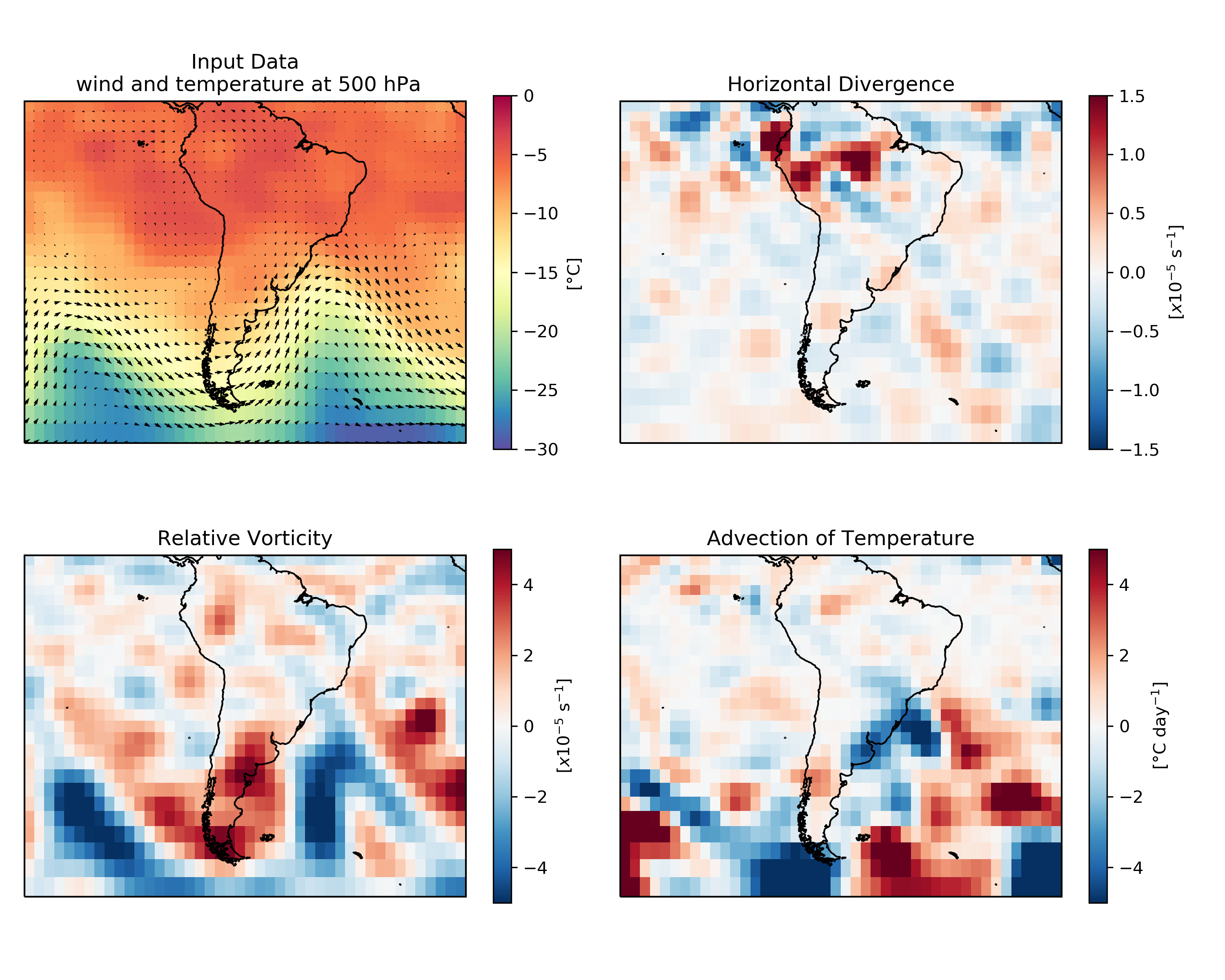
dudx = mg.cdiff(u, axis=0)/mg.cdiff(lonv*np.pi/180)Note that the data are from thr 500 hPa level, so the wind is basically geostrophic. Therefore, not much divergece results in the vicinities of the jet.
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(2,2,1,projection=ccrs.Mercator())
ax.set_extent([-120, -10, -60, 10], crs=ccrs.PlateCarree())
ax.coastlines(resolution='50m')
mesh = ax.pcolormesh(lon, lat,t-273.5, vmin=-30,vmax=0, transform=ccrs.PlateCarree(), cmap="Spectral_r")
cbar=plt.colorbar(mesh, shrink=0.75,label='[°C]')
q = ax.quiver(lon, lat, u, v, minlength=0.1, scale_units='xy',scale=0.0001, transform=ccrs.PlateCarree(), color='k',width=0.003)
plt.title('Input Data\n wind and temperature at 500 hPa')
ax = fig.add_subplot(2,2,2,projection=ccrs.Mercator())
ax.set_extent([-120, -10, -60, 10], crs=ccrs.PlateCarree())
ax.coastlines(resolution='50m')
mesh = ax.pcolormesh(lon, lat, div*100000, vmin=-1.5,vmax=1.5, transform=ccrs.PlateCarree(), cmap="RdBu_r")
cbar=plt.colorbar(mesh, shrink=0.75,label='[$x10^{-5}$ s$^{-1}$]')
plt.title('Horizontal Divergence')
ax = fig.add_subplot(2,2,3,projection=ccrs.Mercator())
ax.set_extent([-120, -10, -60, 10], crs=ccrs.PlateCarree())
ax.coastlines(resolution='50m')
mesh = ax.pcolormesh(lon, lat, vort*100000, vmin=-5,vmax=5, transform=ccrs.PlateCarree(), cmap="RdBu_r")
cbar=plt.colorbar(mesh, shrink=0.75,label='[$x10^{-5}$ s$^{-1}$]')
plt.title('Relative Vorticity')
ax = fig.add_subplot(2,2,4,projection=ccrs.Mercator())
ax.set_extent([-120, -10, -60, 10], crs=ccrs.PlateCarree())
ax.coastlines(resolution='50m')
mesh = ax.pcolormesh(lon, lat, tadv*84600, vmin=-5,vmax=5, transform=ccrs.PlateCarree(), cmap="RdBu_r")
cbar=plt.colorbar(mesh, shrink=0.75,label='[°C day$^{-1}$]')
plt.title('Advection of Temperature')
plt.tight_layout()
fig.savefig('example.png', dpi=300)