-
Notifications
You must be signed in to change notification settings - Fork 23
[Q&A for CMU Neural Networks for NLP 2018]
Perplexity(이하 PPL)는 어떤 시점에서 정답을 선택하기 위해 선택해야 하는 후보의 평균 갯수를 의미합니다. PPL이 60이라면 매 순간마다 60개의 후보를 내야 정답을 고를 수 있다는 말이죠. 정보 이론에서, PPL은 어떤 확률 분포나 확률 모델이 하나의 실제 관측치를 얼마나 잘 예측하는 지를 보여주는 척도로 쓰입니다.
우리가 해결해야 할 문제가 문장을 읽고 다음에 나올 단어를 예측하는 문제이고, 우리가 가진 단어의 갯수가 20,000개라고 가정해 봅시다. 만약 모든 단어의 출현 확률이 같다면(그럴리는 없겠지만) 다음 단어의 선택 가능의 수는 모두 동일하므로 20,000개를 후보로 둬야 정답이 나오게 됩니다. 이 때의 PPL은 20,000이 되는 것이죠. 다만 우리가 좀더 나은 Language model을 만들어서 다음에 선택할 수 있는 단어의 갯수가 평균적으로 30개정도 나왔을 때 정답을 찾을 수 있다면, PPL은 30이 되고, 더 나은 모델이라고 평가할 수 있죠.
수식으로 생각하면 더 쉬워집니다. PPL은 다음과 같은 식인데요,
여기서 는 선택가능한 하나의 경우의 수이고,
는 해당 probability model이 예측하는
의 확률입니다. 모든
가 단순 random picking인
이라면 PPL은
가 되지만, 완벽한 모델이 만들어져서
가 1개 빼고 다 0이 된다면 1이 됩니다.
-
perplexity vs cross-entropy?
간단합니다. 위의 식에서
$H(p)$ 가 곧 cross-entropy 값입니다. 즉 다음과 같습니다. -
perplexity가 낮다 == 모델의 성능이 좋다?
이는 probability distribution의 PPL을 볼 것이냐와 probability model의 PPL을 볼 것이냐에 따라 조금 달라집니다. 해당 task 자체의 난이도를 평가하기 위해서 probability distribution의 PPL을 보게 되는데, 예를 들면 "다음 주사위의 숫자를 맞추기" vs "다음 동전의 면을 맞추기" 라고 두 개의 task를 비교할 때, 전자는 PPL이 최대 6이고, 후자는 PPL이 최대 2이므로 후자가 더 쉬운 task입니다. 다른 관점에서, 같은 task 내에 여러 probability model들이 있을 때, A라는 모델이 B라는 모델보다 PPL이 더 낮다면, A라는 모델이 B라는 모델보다는 성능이 좋다고 할 수 있죠.
Pointwise Mutual Information(PMI)는 두 단어 사이의 관계 정도를 재는 척도입니다.
두 단어가 독립적이라면 결합확률은 개별확률의 곱과 같아지기 때문에 PMI(x, y) = 0이 됩니다. 반대로 두 단어가 함께 출현하는 빈도가 잦다면 PMI는 1보다 커집니다. 예컨대, ("ice", "cream"), ("New, York") 같은 단어쌍들은 PMI가 높죠.
PMI는 Information theory의 Mutual information에서 온 개념인데요. Mutual Information이 모든 가능한 경우의 평균을 말한다면 Pointwise Mutual Information은 하나의 경우만을 말합니다.
더 알아보고 싶으시다면 다음 자료를 참고해주세요.
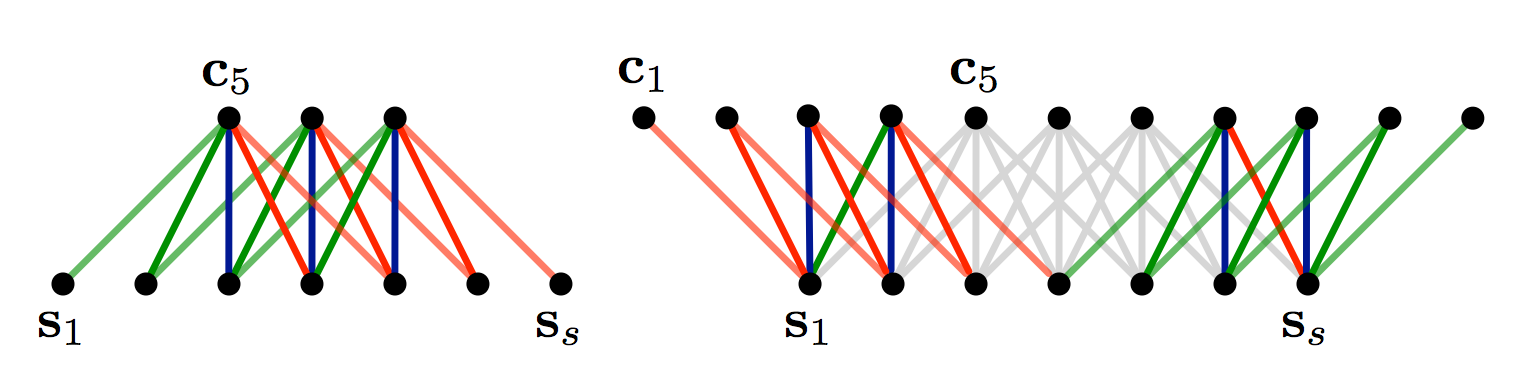
CMU 강의에서 wide convolution의 장점에 대해서 언급하였는데, padding을 문장의 시작과 끝을 나타내는 token으로 줌으로써 문장의 경계에 있는 단어를 잘 포착할 수 있다고 합니다. 위의 wide convolution 그림을 예로 들었을 때, 맨 앞에 문장의 시작을 나타내는 임의의 token을 padding을 주면 output vector의 제일 첫번째 element는 시작 token과 첫 단어에 convolution을 취한 결과로 계산됩니다. 이렇게 경계에 있는 feature를 잘 파악할 수 있기 때문에 wide convolution을 사용한다고 합니다.
k-max pooling은 주어진 k 값에 대해 sequence P에서 상위 k개의 값을 추출하는 pooling 방식입니다. P에서 제일 큰 하나만 추출하는 max-pooling과는 다릅니다. 상위 k개의 값을 추출할 때 그 순서는 원래 P 안에서의 순서와 같습니다. k-max pooling을 통하여 떨어져 있는 p개의 active position을 추출할 수 있습니다. 이는 feature의 순서는 유지하지만, 그 각각의 특정 position은 무시하게 됩니다.
dynamic k-max pooling은 중간 단계의 convolution layers에서 k 값이 고정되어있지 않고, 현재 layer의 depth와 문장의 길이에 따라 dynamic하게 결정되는 방식을 말합니다. 대표적으로 Kalchbrenner at el의 A Convolutional Neural Network for Modelling Sentences에서 dynamic k-max pooling을 사용하였는데 pooling parameter k를 다음과 같은 식으로 결정하였습니다.
l은 현재 convolution layer의 depth, L은 network 안의 전체 convolution layer의 개수, k_top은 가장 상위 convolution layer의 k 값으로 고정되어 있습니다.
-
Precision
- (검색 시스템) 검색된 문서 중 relevant한 문서의 비율
- 즉, Model이 1이라고 분류한 것들 중 실제 1의 비율
$Precision = \frac{TP}{TP + FP}$
-
Recall
- (검색 시스템) Relevant한 문서 중 검색된 비율
- 실제 1인 것들 중 Model이 1이라고 분류한 비율
$Recall = \frac{TP}{TP + FN}$
-
Precision vs Recall
- 둘다 단점이 있다. 모두가 1이라고 분류하면 Recall이 1이 되고, 모두가 0이라고 분류하면 Precision이 1이 된다. 따라서 이를 둘다 고려하거나(f1 score, AUROC), 상황을 가정하고 하나만 고려하는 경우 (Precision at k, MAP), 실제 1이 얼마나 뒤에 rank되는 지를 고려하는 경우(nDCG)이 있다.
- 보통 검색 시스템이 모델이 가장 relevant하다고 판단한 k개의 결과만 보여준다는 측면에서 자주 사용되는 방식이다.
- P@k 는 모델이 가장 relevant하다고 판단한 k개 중 실제 relevant한 비율이다.
- 단점 1 : 그 k개 안에서 실제 1이 얼마나 상위에 rank되는 지는 고려하지 못한다
- 단점 2 : k개 안에서 실제 1의 갯수가 적을 수록 아무리 좋은 모델이라도 점수가 낮아지는 경향이 있다.
주어진 Test Query들이 있을 때, 각각의 Query에 대해 Average Precision을 예측한 뒤 이를 평균낸 값이다.
- Precision-Recall Curve
- Average precision을 알려면 일단 precision-recall curve에 대해 이해해야 하는데, 모델의 성능이나 positive의 비율에 따라 precision과 recall은 다음과 같은 분포를 이루게 된다. 이 때 각각의 precision과 recall이 결정되는 기준은 classification threshold이고, 같은 모델에 대해서도 query가 어떤게 들어오느냐에 따라 그래프가 달라진다.

- 왼쪽 그림은 모델의 성능이 좋거나, positive의 갯수가 많은 것이다. 어떻게 되었든 오른쪽보다는 좋다고 볼 수 있는데, 같은 모델이어도 classification threshold에 따라 그 값이 달라지기 때문에 전체적인 모델의 성능을 평가하기 위해 Mean Precision을 계산한다. 그렇게 되면 왼쪽 그림은 0.88이 되고, 오른쪽 그림은 0.43이 된다.
- 위의 그림은 하나의 모델이 하나의 query에 대해 예측한 것을 가지고 판단한 것이다. 다양한 Test query에 대해 평가하기 위해 Q개의 query가 있다면 그들의 AP를 평균낸 것이 MAP이다.
- 단순 classification 모델도 probability에 따라 ranking을 매길 수 있다. Retrieval System에서는 이 ranking이 매우 중요한데, 결국 하위로 rank한 것 중에 1이 얼마나 아래 있는지와 상위로 rank한 것 중이 1이 얼마나 위에 있는지도 평가 기준에 넣기 위해서이다.
- 하나의 position
$p$ 에 대한 DCG는 다음과 같이 계산한다. $$ DCG_{p} = rel_1 + \sum_{i=2}^{p} \frac{rel_i}{log_2i} $$ - 여기서
$rel_i$ 는 i번째 rank된 query가 positive인지의 여부이고(때에 따라서 scale 변경 가능) 수식을 보면 후순위에 1이 있을 수록 discounted된다. 특히 여기에$log$ 를 쓴 이유는, 1위와 2위는 큰 차이지만, 999위와 1000위는 별로 차이가 없기 때문이다. - 그런데 이러면, 각각의 query에 대해 positive의 갯수가 달라질 수 있으므로 정확하지 않아서, 해당 모델과 해당 쿼리에 대한
$DCG$ 를 해당 쿼리가 가질 수 있는 최고의$DCG$ (이상적인 score)로 나눈 값이 바로$_{n}DCG$ 이다.

