A repo with an introduction to cryptography, resources and info.
- https://medium.com/coinmonks/cryptography-for-beginners-d458cdcdd6d2
- https://medium.com/@ahjuice/cryptography-what-is-it-and-how-does-it-work-2a21a730d694
- https://medium.com/@vixentael/how-to-start-learning-cryptography-49e7d91b54a8
- https://www.crypto101.io/
- https://cryptopals.com/ (Code Challenges for Basic Crypto Concepts)
- https://docs.python-guide.org/scenarios/crypto/
- https://medium.com/@raul_11817/rsa-with-cryptography-python-library-462b26ce4120
- https://medium.com/@ismailakkila/black-hat-python-encrypt-and-decrypt-with-rsa-cryptography-bd6df84d65bc
- https://medium.freecodecamp.org/how-to-create-a-bitcoin-wallet-address-from-a-private-key-eca3ddd9c05f
Cryptography is a method of storing and transmitting data in a particular form so that only those for whom it is intended can read and process it.
Cryptography includes techniques such as microdots, merging words with images, and other ways to hide information in storage or transit. Cryptography is most often associated with scrambling plaintext (ordinary text, sometimes referred to as cleartext) into ciphertext (a process called encryption), then back again (known as decryption).
Modern cryptography concerns itself with the following four objectives:
-
Confidentiality (the information cannot be understood by anyone for whom it was unintended)
-
Integrity (the information cannot be altered in storage or transit between sender and intended receiver without the alteration being detected)
-
Non-repudiation (the creator/sender of the information cannot deny at a later stage his or her intentions in the creation or transmission of the information)
-
Authentication (the sender and receiver can confirm each other?s identity and the origin/destination of the information)
Output of XOR is 1 when one input or the other (but not both) is 1:
0 ⊕ 0 = 0
1 ⊕ 0 = 1
0 ⊕ 1 = 1
1 ⊕ 1 = 0
There are a few useful arithmetic tricks we can derive from that.
-
You can apply XOR in any order: a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c
-
You can flip the operands around: a ⊕ b = b ⊕ a
-
Any bit XOR itself is 0: a ⊕ a = 0. If a is 0, then it’s 0 ⊕ 0 = 0.
-
Any bit XOR 0 is that bit again: a ⊕ 0 = a. If a is 0, then it’s 0 ⊕ 0 = 0.
These rules also imply a ⊕ b ⊕ a = b: a ⊕ b ⊕ a = a ⊕ a ⊕ b (second rule) = 0 ⊕ b (third rule) = b (fourth rule)
There’s an encryption scheme, called a one-time pad, which consists of just that single operator. It’s called a one-time pad because it involves a sequence (the ”pad”) of random bits, and the security of the scheme depends on only using that pad once. This scheme is unique not only in its simplicity, but also because it has the strongest possible security guarantee. If the bits are truly random (and therefore unpredictable by an attacker), and the pad is only used once, the attacker learns nothing about the plaintext when they see a ciphertext.
The one-time pad security guarantee only holds if it is used correctly. First of all, the one-time pad has to consist of truly random data. Secondly, the one-time pad can only be used once (hence the name). Unfortunately, most commercial products that claim to be ”one-time pads” are snake oil , and don’t satisfy at least one of those two properties.
The first issue is that they use various deterministic constructs to produce the one-time pad, instead of using truly random data. That isn’t necessarily insecure: in fact, the most obvious example, a synchronous stream cipher, is something we’ll see later in the book. However, it does invalidate the ”unbreakable” security property of one-time pads. The end user would be better served by a more honest cryptosystem, instead of one that lies about its security properties.
The other issue is with key reuse, which is much more serious. Suppose an attacker gets two ciphertexts with the same ”one-time” pad. The attacker can then XOR the two ciphertexts, which is also the XOR of the plaintexts:
c1 ⊕ c2 = (p1 ⊕ k) ⊕ (p2 ⊕ k) (definition)
= p1 ⊕ k ⊕ p2 ⊕ k (reorder terms)
= p1 ⊕ p2 ⊕ k ⊕ k (a ⊕ b = b ⊕ a)
= p1 ⊕ p2 ⊕ 0 (x ⊕ x = 0)
= p1 ⊕ p2 (x ⊕ 0 = x)
At first sight, that may not seem like an issue. To extract either p1 or p2, you’d need to cancel out the XOR operation, which means you need to know the other plaintext. The problem is that even the result of the XOR operation on two plaintexts contains quite a bit information about the plaintexts themselves.
A hash function is simply a function that takes in input value, and from that input creates an output value deterministic of the input value. For any x input value, you will always receive the same y output value whenever the hash function is run. In this way, every input has a determined output.
This is the hash function md5, which from any input data creates a 32 character hexadecimal output. Hash functions are generally irreversible (one-way), which means you can’t figure out the input if you only know the output – unless you try every possible input (which is called a brute-force attack).
SHA-1 is another hash function from the MD4 family designed by the NSA, which produces a 160-bit digest. Just like MD5, SHA-1 is no longer considered secure for digital signatures. Many software companies and browsers, including Google Chrome, have started to retire support of the signature algorithm of SHA-1. Once again the hashlib Python module can be used to generate a SHA-1 hash:
import hashlib
hashlib.sha1(”crypto101”).hexdigest()
SHA-2 is a family of hash functions including SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224 and SHA-512/256 and their digest sizes 224, 256, 384, 512, 224 and 256 respectively. These hash can be used for digital signatures, message authentication and random number generators. SHA-2 performs better than SHA-1 and provides better security, because of its increase in collision resistance. SHA-224 and SHA-256 were designed for 32-bit processor registers, while SHA-384 and SHA-512 for 64-bit registers. The 32-bit register variants will therefore run faster on a 32-bit CPU and the 64-bit variants will perform better on a 64-bit CPU. SHA-512/224 and SHA-512/256 are truncated versions of SHA-512 allowing use of 64-bit words with an output size equivalent to the 32-bit register variants (i.e., 224 and 256 digest sizes and better performance on a 64-bit CPU).
Keccak is a family of sponge functions designed by which won NIST’s Secure Hash Algorithm Competition in 2012. Keccak has since been standardized in form of the SHA3-224, SHA3-256, SHA3-384 and SHA3-512 hash functions. Although SHA-3 sounds like it might come from the same family as SHA-2, the two are designed very differently. SHA-3 is very efficient in hardware, but is relatively slow in software in comparison to SHA-2. Later in the book, you will find the security aspects of SHA-3, such as preventing length extension attacks.
The Caesar cipher, also known as a shift cipher, is one of the simplest forms of encryption. It is a substitution cipher where each letter in the original message (called the plaintext) is replaced with a letter corresponding to a certain number of letters up or down in the alphabet.
In this way, a message that initially was quite readable, ends up in a form that can not be understood at a simple glance.
For example, here's the Caesar Cipher encryption of a message, using a right shift of 3.
Plaintext:
THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG
Ciphertext:
QEB NRFZH YOLTK CLU GRJMP LSBO QEB IXWV ALD
Although most people claim they're not familiar with cryptography, they are often familiar with the concept of ciphers, whether or not they are actually conscious of it. Ciphers are arguably the corner stone of cryptography. In general, a cipher is simply just a set of steps (an algorithm) for performing both an encryption, and the corresponding decryption.
Despite might what seem to be a relatively simple concept, ciphers play a crucial role in modern technology. Technologies involving communication (including the internet, mobile phones, digital television or even ATMs) rely on ciphers in order to maintain both security and privacy.
Although most people claim they're not familiar with cryptography, they are often familiar with the concept of ciphers, whether or not they are actually conscious of it. Recent films such as The Da Vinci Code and National Treasure: Book of Secrets have plots centred around cryptography and ciphers, bringing these concepts to the general public.
This section (quite appropriately) deals with individual ciphers and algorithms. They have been divided based on their era and category (i.e. when were they used and how do they work). If you're looking for a reference guide, refer to the alphabetical list to the right, otherwise continue reading.
In our effort to provide a practical approach to these, we have developed a javascript implementation for each cipher that allows encryption and decryption of arbitrary text (of your choosing) using the cipher. Some history of each cipher is also included, and tips on cryptanalysis are also provided.
The Affine Cipher is another example of a Monoalphabetic Substituiton cipher.
It is slightly different to the other examples encountered before since the encryption process is
substantially mathematical.
The whole process relies on working modulo m (the length of the alphabet used).
By performing a calculation on the plaintext letters, we encipher the plaintext.
Encryption
The first step in the encryption process is to transform each of the letters in the plaintext
alphabet to the corresponding integer in the range 0 to m-1.
With this done, the encryption process for each letter is given by
E(x) = (ax + b) mod m
where a and b are the key for the cipher.
This means that we multiply our integer value for the plaintext letter by a, and then add b to the result.
Finally, we take this modulus m (that is we take the remainder when the solution is divided by m,
or we take away the length of the alphabet until we get a number less than this length).
Example
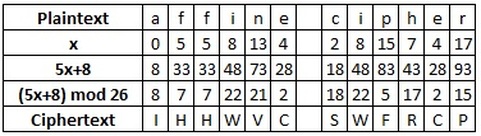
As an example, let us encrypt the plaintext "affine cipher", using the key a = 5, b = 8.
Firstly we must find the integer value of each of the letters in the plaintext alphabet
(the standard alphabet of 26 letters in this case).
The table below gives these values.
With the integer values of the plaintext letters found, the next step is to perform the calculations
on those values.
In this instance, the calculation needed is (5x+8).
Finally, we must ensure that all our answers are calculated mod 26 and convert the
integers back to ciphertext lettes.
All the informaion is shown in the table below.
Decryption
In deciphering the ciphertext, we must perform the opposite (or inverse) functions on the
ciphertext to retrieve the plaintext.
Once again, the first step is to convert each of the ciphertext letters into their integer values.
We must now perform the following calculation on each integer
D(x) = c(x - b) mod m
where c is the modular multiplicative inverse of a.
That is, ac = 1 mod m
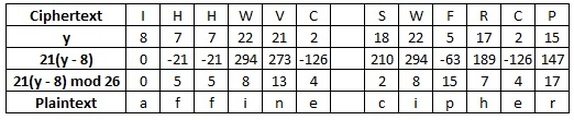
Continuing our example, we shall decrypt the ciphertext "IHHWVC SWFRCP",
using a key of a = 5, b = 8.
The first step here is to find the inverse of a, which in this case is 21
(since 21 x 5 = 105 = 1 mod 26, as 26 x 4 = 104, and 105 - 104 = 1).
We must now perform the inverse calculations on the integer values of the ciphertext.
In this case the calculation in 21(y - 8).
Once again, we must take these answers modulo 26, and finally convert the integers back to plaintext letters.
This is shown in the table below.
Important Note - For decryption c must exist => only those values of a will work such that gcd(a,m) = 1.