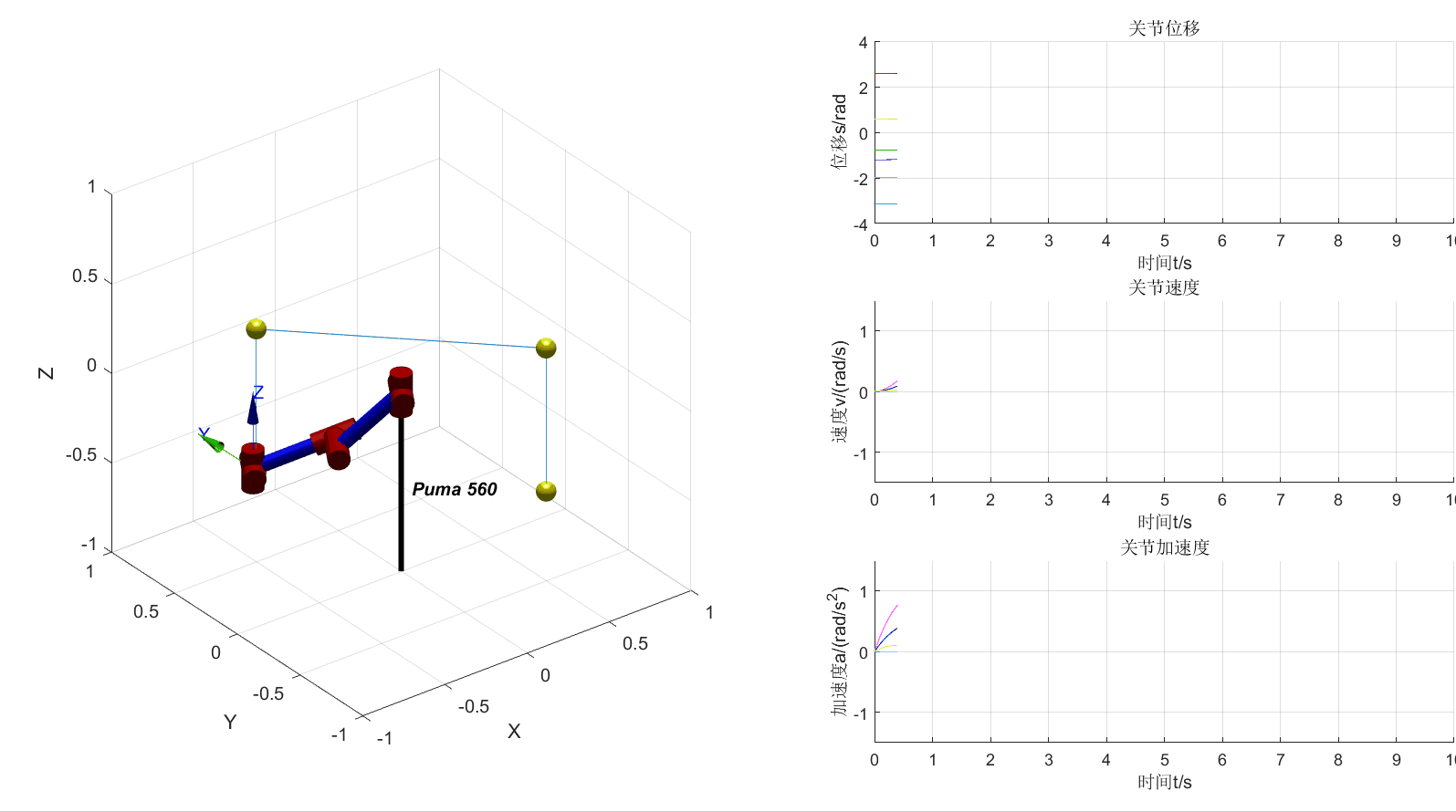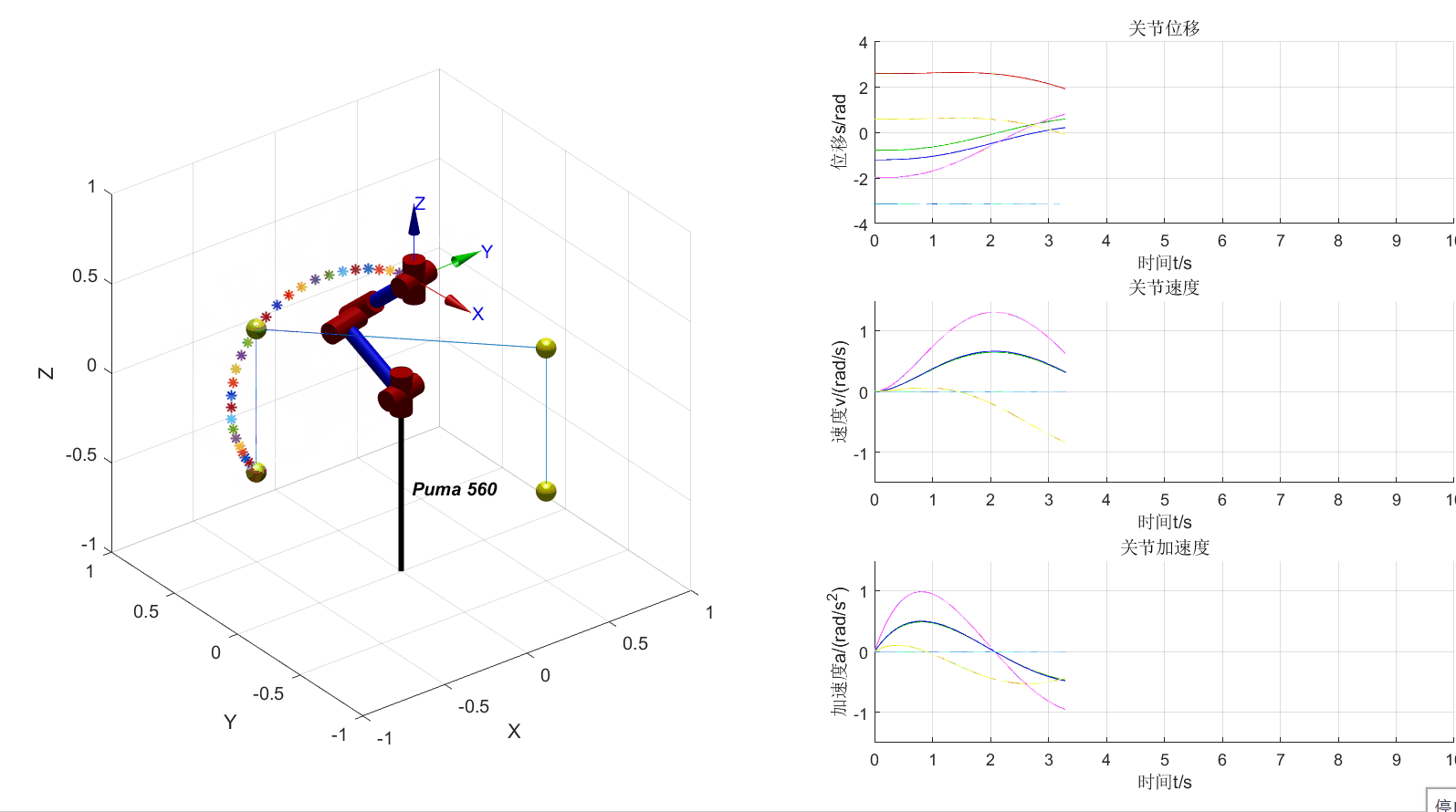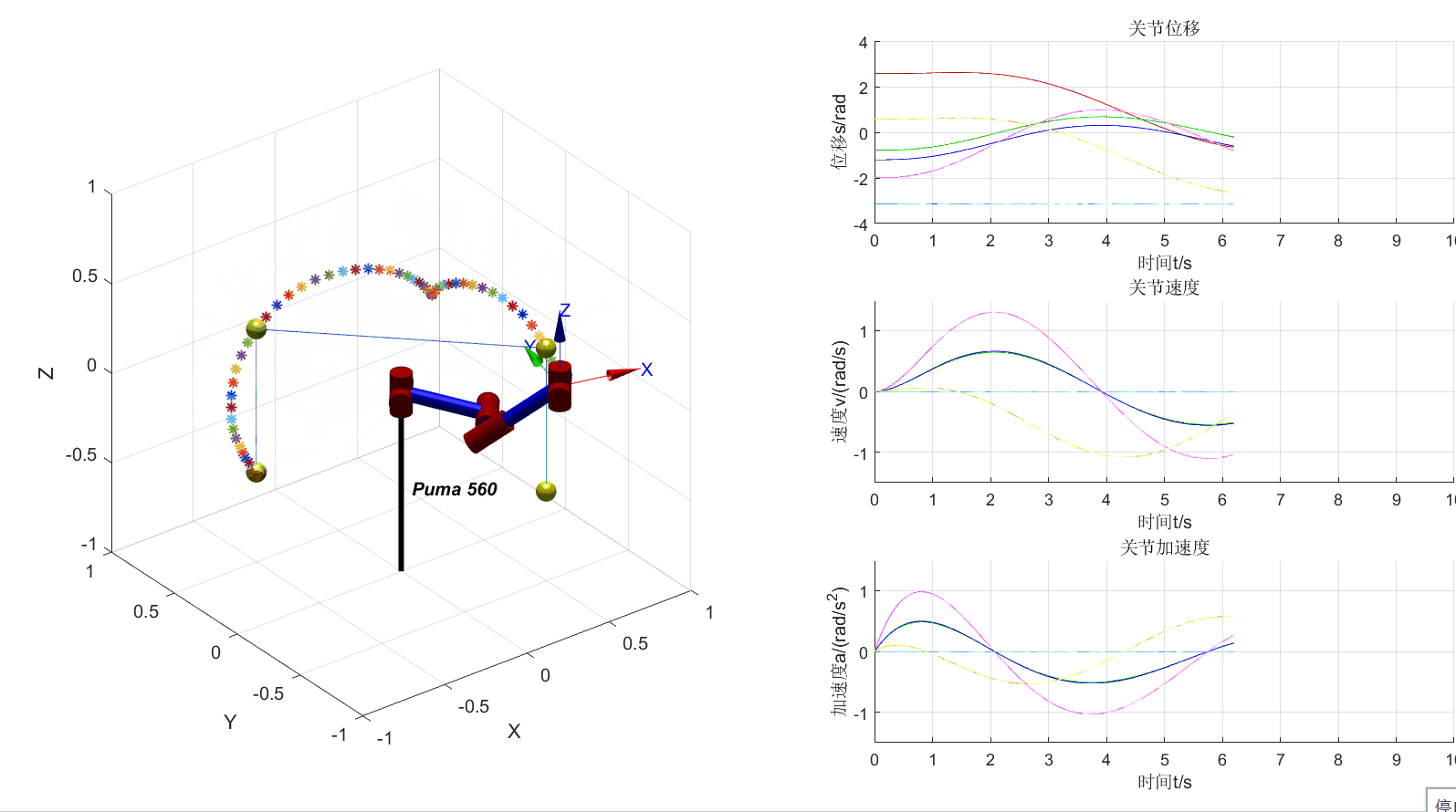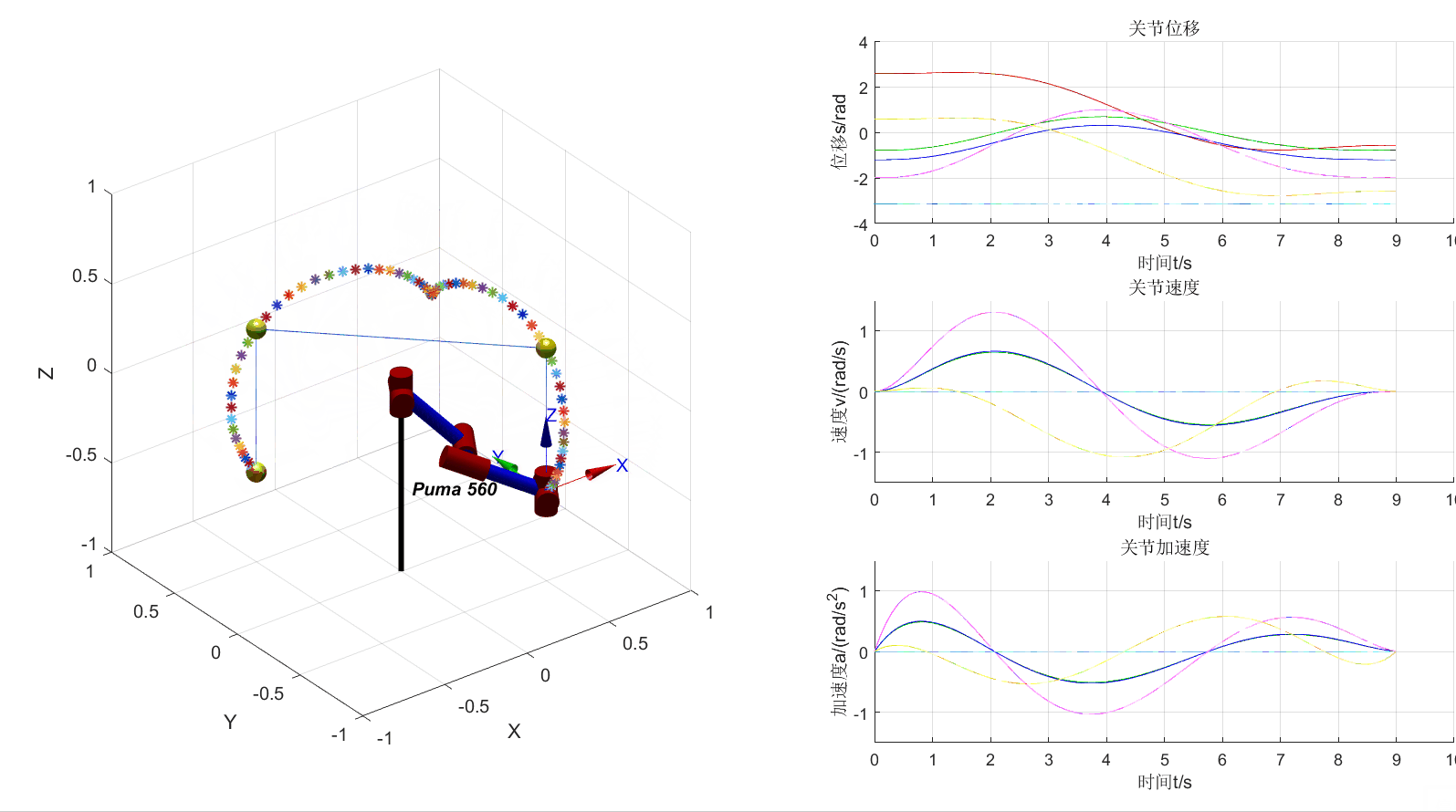
Based on PUMA560
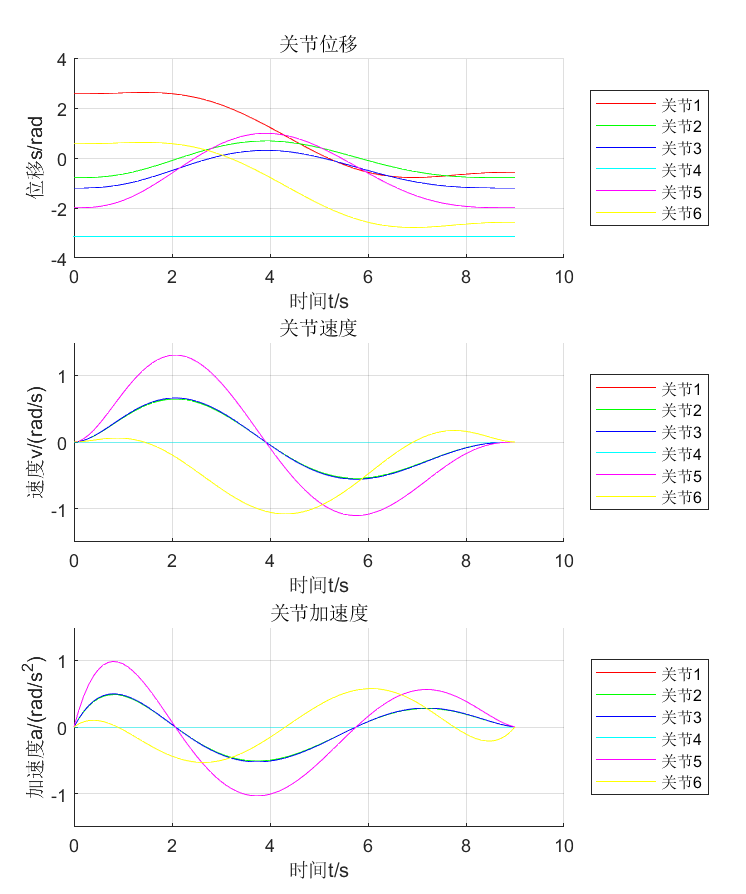
动态绘制位移、速度、加速度曲线
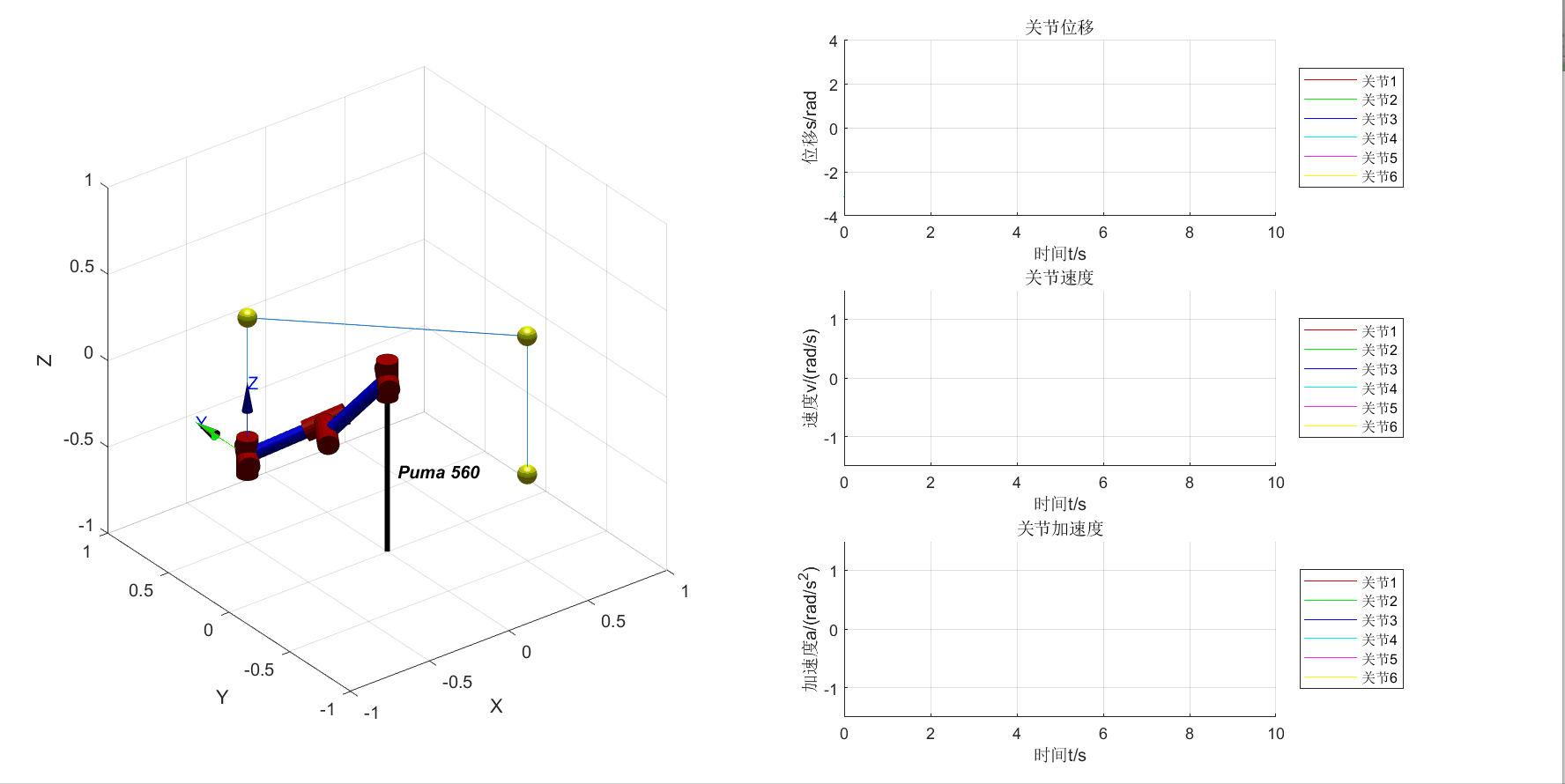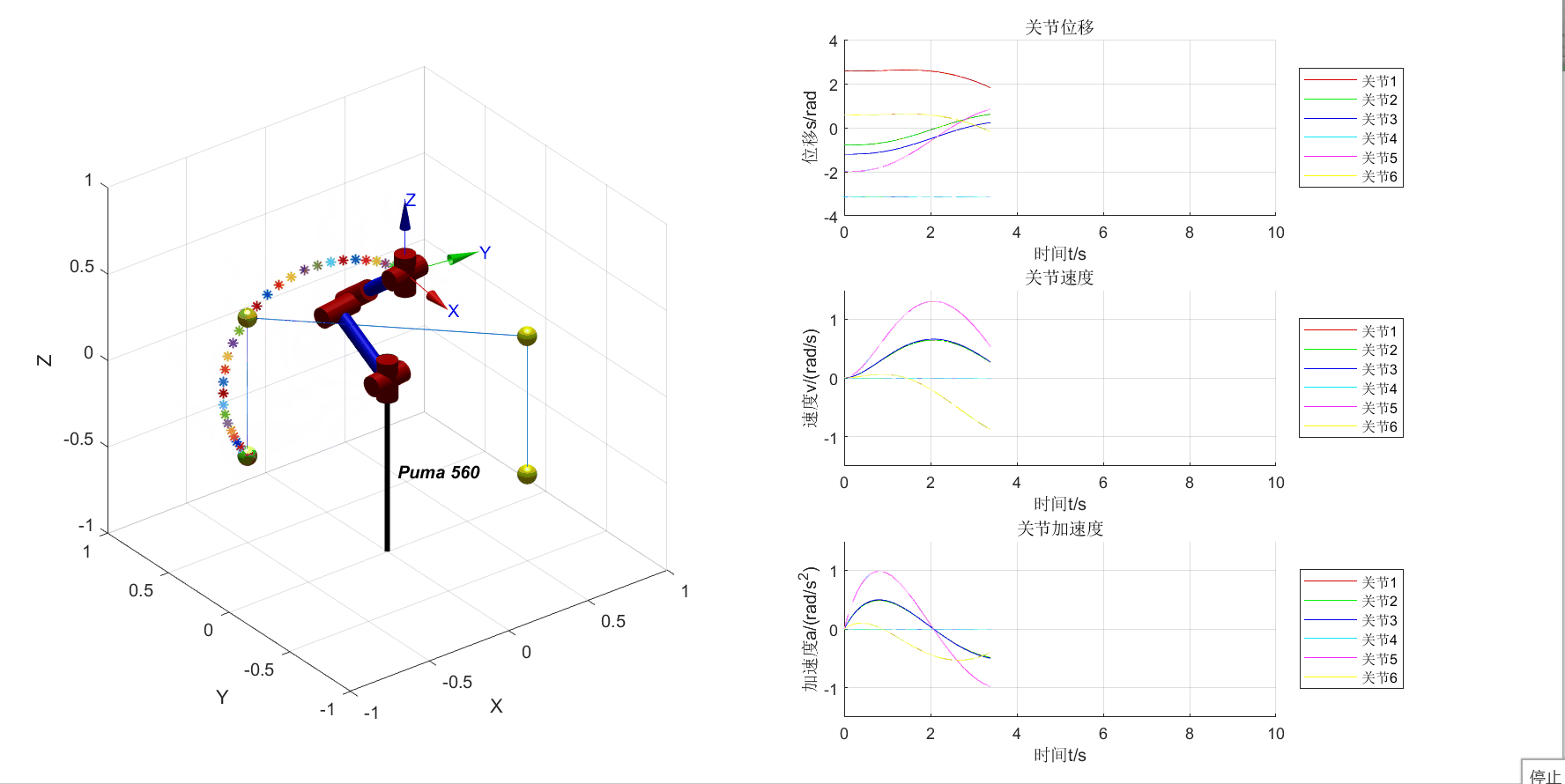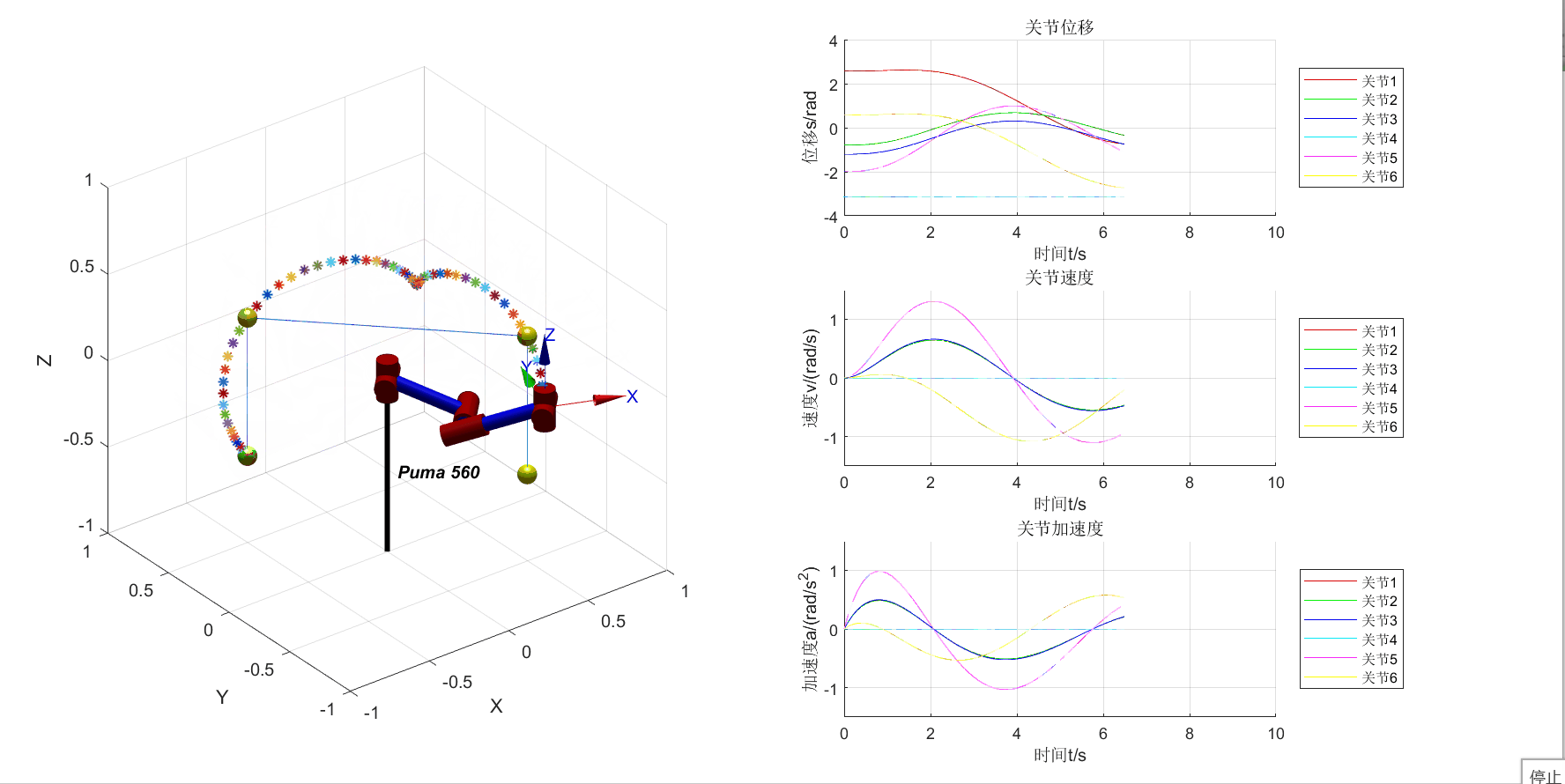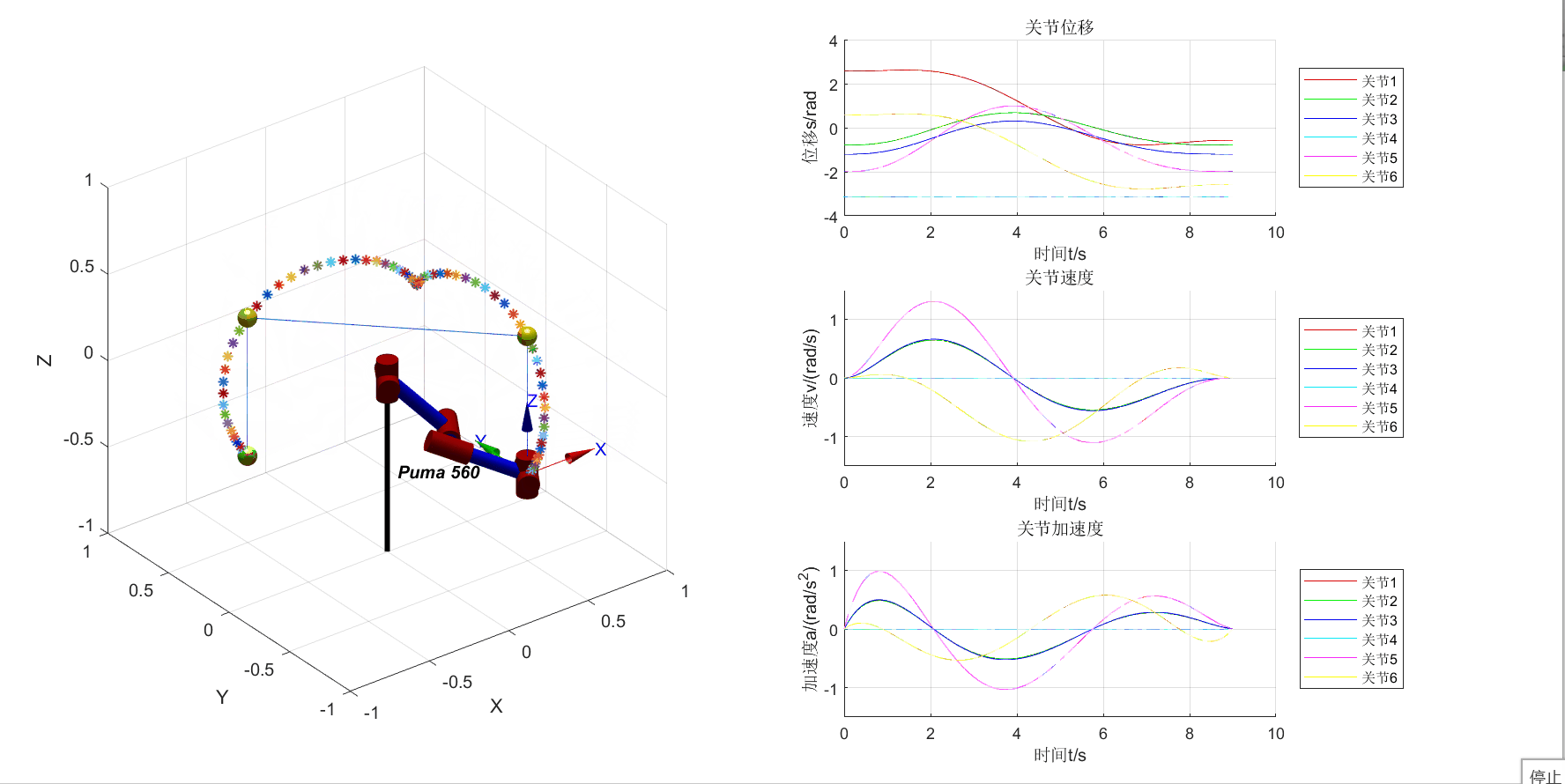
将机器人的3D视图和位移、速度、加速度曲线画在一个figure中
增加4个中间点和3段直线轨迹的可视化
先计算好轨迹,再在另一个for循环中画图,以提高绘图速度
实验3:取-放轨迹规划——7次多项式轨迹的规划@[toc]
- 掌握典型的取-放轨迹规划方法
- 参考所学,完成7次多项式实现的典型取-放轨迹。
- 其中取放作业应包含起始位置(取点)、转移位置(抬起或离开点)、卸下位置(下降点)和目标位置(放置点),整理出边界条件和连续条件。
- 列出轨迹未知系数的推导过程并形成类似于课本式(5.33)或(5.34)的求解式。
- 使用Matlab Robotics 取得PUMA560机器人末端的任一组取-放作业的四个位置点,经逆解得各关节的位置。
- 此外,假设起始位置、目标位置的关节速度和加速度都设为0,三段的运动时间分别是2s,4s和3s。接着,使用Matlab求解出轨迹的未知系数,生成PUMA560各关节的位置、速度和加速度的轨迹函数。
- 将这些轨迹输入Matlab Robotics的PUMA560中,仿真执行取放轨迹,观察其与三段直线轨迹的执行结果的差别并分析原因。
- 实验报告需绘制出轨迹的位置、速度和加速度的曲线,并与三段直线轨迹的进行对比。
MATLAB, robotics toolbox
- 初始位置:$$\theta(0)=\theta_{0}=c_{0}$$
- 初始速度:$$\dot{\theta}(0)=\dot{\theta}{0}=c{1}$$
- 初始加速度:$$\ddot{\theta}(0)=\ddot{\theta}{0}=2c{2}$$
- 目标位置:$$\theta(t_{f})=\theta_{f}=c_{0}+c_{1}t_{f}+c_{2}t_{f}^2+c_{3}t_{f}^3+c_{4}t_{f}^4+c_{5}t_{f}^5+c_{6}t_{f}^6+c_{7}t_{f}^7$$
- 目标速度:$$\dot{\theta}(t_{f})=\dot{\theta}{f}=c{1}+2c_{2}t_{f}+3c_{3}t_{f}^2+4c_{4}t_{f}^3+5c_{5}t_{f}^4+6c_{6}t_{f}^5+7c_{7}t_{f}^6$$
- 目标加速度:$$\ddot{\theta}(t_{f})=\ddot{\theta}{f}=2c{2}+6c_{3}t_{f}+12c_{4}t_{f}^2+20c_{5}t_{f}^3+30c_{6}t_{f}^4+42c_{7}t_{f}^5$$
- t1时刻位置:$$\theta(t_{1})=\theta_{1}=c_{0}+c_{1}t_{1}+c_{2}t_{1}^2+c_{3}t_{1}^3+c_{4}t_{1}^4+c_{5}t_{1}^5+c_{6}t_{1}^6+c_{7}t_{1}^7$$
- t2时刻位置:$$\theta(t_{2})=\theta_{2}=c_{0}+c_{1}t_{2}+c_{2}t_{2}^2+c_{3}t_{2}^3+c_{4}t_{2}^4+c_{5}t_{2}^5+c_{6}t_{2}^6+c_{7}t_{2}^7$$
七次多项式如下:
代入约束条件可得:
$$\begin{cases} \theta(0)=\theta_{0}=c_{0}\ \dot{\theta}(0)=\dot{\theta}{0}=c{1}\ \ddot{\theta}(0)=\ddot{\theta}{0}=2c{2}\ \theta(t_{1})=\theta_{1}=c_{0}+c_{1}t_{1}+c_{2}t_{1}^2+c_{3}t_{1}^3+c_{4}t_{1}^4+c_{5}t_{1}^5+c_{6}t_{1}^6+c_{7}t_{1}^7\ \theta(t_{2})=\theta_{2}=c_{0}+c_{1}t_{2}+c_{2}t_{2}^2+c_{3}t_{2}^3+c_{4}t_{2}^4+c_{5}t_{2}^5+c_{6}t_{2}^6+c_{7}t_{2}^7\ \theta(t_{f})=\theta_{f}=c_{0}+c_{1}t_{f}+c_{2}t_{f}^2+c_{3}t_{f}^3+c_{4}t_{f}^4+c_{5}t_{f}^5+c_{6}t_{f}^6+c_{7}t_{f}^7\ \dot{\theta}(t_{f})=\dot{\theta}{f}=c{1}+2c_{2}t_{f}+3c_{3}t_{f}^2+4c_{4}t_{f}^3+5c_{5}t_{f}^4+6c_{6}t_{f}^5+7c_{7}t_{f}^6\ \ddot{\theta}(t_{f})=\ddot{\theta}{f}=2c{2}+6c_{3}t_{f}+12c_{4}t_{f}^2+20c_{5}t_{f}^3+30c_{6}t_{f}^4+42c_{7}t_{f}^5\ \end{cases}$$
可写成如下的矩阵形式:
$$\begin{bmatrix} \theta_{0}\ \dot{\theta}{0}\ \ddot{\theta}{0}\ \theta_{1}\ \theta_{2}\ \theta_{f}\ \dot{\theta}{f}\ \ddot{\theta}{f}\ \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\ 0 & 0 & 2 & 0 & 0 & 0 & 0 & 0\ 1 & t_{1} & t_{1}^2 & t_{1}^3 & t_{1}^4 & t_{1}^5 & t_{1}^6 & t_{1}^7\ 1 & t_{2} & t_{2}^2 & t_{2}^3 & t_{2}^4 & t_{2}^5 & t_{2}^6 & t_{2}^7\ 1 & t_{f} & t_{f}^2 & t_{f}^3 & t_{f}^4 & t_{f}^5 & t_{f}^6 & t_{f}^7\ 0 & 1 & 2t_{f} & 3t_{f}^2 & 4t_{f}^3 & 5t_{f}^4 & 6t_{f}^5 & 7t_{f}^6\ 0 & 0 & 2 & 6t_{f} & 12t_{f}^2 & 20t_{f}^3 & 30t_{f}^4 & 42t_{f}^5\ \end{bmatrix} \times \begin{bmatrix} c_{0}\c_{1}\c_{2}\c_{3}\c_{4}\c_{5}\c_{6}\c_{7} \end{bmatrix} $$
或表示为
和
- 初始位置:$(-0.5,0.5,-0.5)$
- t1时刻位置:$(-0.5,0.5,0.3)$
- t2时刻位置:$(0.5,-0.5,0.3)$
- 目标位置:$(0.5,-0.5,-0.5)$
| 位置 | 关节1 | 关节2 | 关节3 | 关节4 | 关节5 | 关节6 |
|---|---|---|---|---|---|---|
| 起始位置 | 2.5700 | -0.7873 | -1.2022 | -3.1416 | -1.9895 | 0.5716 |
| 转移位置 | 2.5700 | -0.1026 | -0.5000 | -3.1416 | -0.6026 | 0.5716 |
| 卸下位置的关节角 | -0.5716 | -0.1026 | -0.5000 | -3.1416 | -0.6026 | -2.5700 |
| 目标位置的关节角 | -0.5716 | -0.7873 | -1.2022 | -3.1416 | -1.9895 | -2.5700 |
| 单位:$rad$ |
| 位置 | 关节1 | 关节2 | 关节3 | 关节4 | 关节5 | 关节6 |
|---|---|---|---|---|---|---|
| 2.5700 | -0.7873 | -1.2022 | -3.1416 | -1.9895 | 0.5716 | |
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0938 | 0.2301 | 0.2359 | 0.0000 | 0.4660 | 0.0938 | |
| -0.0750 | -0.1008 | -0.1033 | -0.0000 | -0.2041 | -0.0750 | |
| 0.0169 | 0.0165 | 0.0170 | -0.0000 | 0.0335 | 0.0169 | |
| -0.0015 | -0.0012 | -0.0012 | 0.0000 | -0.0024 | -0.0015 | |
| 0.0001 | 0.0000 | 0.0000 | 0.0000 | 0.0001 | 0.0001 |
| 函数 | 说明 |
|---|---|
| ikcon | 使用关节极限优化的反向运动学 |
| ikine6s | 六轴球形腕关节旋转机器人的逆运动学 |
| ikine | 迭代数值法逆运动学 |
通过阅读ikcon.m文件发现如下注释(已翻译成中文):
- 需要MATLAB优化工具箱中的fmincon函数
- 关节限制在这个解决方法中被考虑。
- 可用于任意自由度的机器人。
- 在有多种可行的解决方案的情况下,这个解决方案的返回依赖于 Q0 的初始选择。
- 工作通过最小化关节角正运动学解决方案和末端位姿的误差作为优化。
- 目标函数(误差)如下:
$$sumsqr( (inv(T)*robot.fkine(q) - eye(4)) * omega )$$ - omega是增益矩阵,现在不可更改
由此可以发现,ikcon是通过优化使得误差最小,从而求得逆解,可见这个逆解是一个数值解。 ikcon中调用的fmincon是MATLAB中的一个用于找到一个有几个变量的函数的最小约束,具体优化问题如下:
min F(X) subject to: AX <= B, AeqX = Beq (linear constraints) X C(X) <= 0, Ceq(X) = 0 (nonlinear constraints) LB <= X <= UB (bounds)
使用ikcon进行的轨迹规划运行结果如上图所示。由于ikcon需要输入初始的关节位置,所以第一个关节的位置是利用ikine6s求得的,代码如下:
theta_0 = p560.ikine6s(T0);
theta_1 = p560.ikcon(T1,theta_0);
theta_2 = p560.ikcon(T2,theta_1);
theta_f = p560.ikcon(Tf,theta_2);仿真结果不尽人意,怀疑是因为是7次多项式插值导致的曲线形状较差,如果给定更多的中间节点,每次迭代换新ikcon的第二个参数——关节位置,逆解效果可能会好很多。
通过阅读ikine6s.m文件发现如下注释(已翻译成中文):
- 解决许多特定情况:
- 没有肩膀偏移的机器人
- 肩膀偏移有左右配置的机器人
- 有一个肩膀偏移和一个棱柱形第三关节(像斯坦福手臂那样)
- 有肩膀和肘部偏移的Puma 560 手臂(四个长度参数)
- 有许多偏移的 Kuka KR5 (七个长度参数)
- 使用ikine_sym定义的各种逆运动学案例.
- 运动学逆解通常不是唯一的,并且取决于配置字符串.
- 关节偏移如果被定义就被添加到逆运动学去生成 Q.
- 仅适用于标准DH参数.
源文件注释中指出,ikine6s求的是解析解。仔细阅读函数源代码后发现,函数中通过手臂结构来判断机器人类型,并且选择相对应的解决方案。
if isempty(robot.ikineType)
if is_simple(L)
robot.ikineType = 'nooffset';
elseif is_puma(L)
robot.ikineType = 'puma';
elseif is_offset(L)
robot.ikineType = 'offset';
elseif is_rrp(L)
robot.ikineType = 'rrp';
else
error('RTB:ikine6s:badarg', 'This kinematic structure not supported');
end
end源文件中对于puma560机器人的判定如下:
function s = is_puma(L)
alpha = [pi/2 0 -pi/2];
s = (L(2).d == 0) && (L(1).a == 0) && ...
(L(3).d ~= 0) && (L(3).a ~= 0) && ...
all([L(1:3).alpha] == alpha) && ...
all([L(1:3).isrevolute] == 1);
end这里的扭转角$alpha$与课堂上PPT里给的[-90,0,90]有区别,故在此次实验中将其改为[90,0,-90]以使得在调用ikine6s时能够将机器人判定为puma560,或者直接修改ikine6s函数源文件中的条件以符合课堂PPT的DH参数也可行。 在判定为puma560后,ikine6s使用解析方法求解$\theta$,相比数值解更加高效、且精度更高。其源代码如下:
case 'puma'
% Puma model with shoulder and elbow offsets
% - Inverse kinematics for a PUMA 560
a2 = L(2).a;
a3 = L(3).a;
d1 = L(1).d;
d3 = L(3).d;
d4 = L(4).d;
% The following parameters are extracted from the Homogeneous
% Transformation as defined in equation 1, p. 34
Ox = T(1,2);
Oy = T(2,2);
Oz = T(3,2);
Ax = T(1,3);
Ay = T(2,3);
Az = T(3,3);
Px = T(1,4);
Py = T(2,4);
Pz = T(3,4) - d1;
%
% Solve for theta(1)
%
% r is defined in equation 38, p. 39.
% theta(1) uses equations 40 and 41, p.39,
% based on the configuration parameter n1
%
r = sqrt(Px^2 + Py^2);
if sol(1) == 1
theta(1) = atan2(Py,Px) + pi - asin(d3/r);
else
theta(1) = atan2(Py,Px) + asin(d3/r);
end
%
% Solve for theta(2)
%
% V114 is defined in equation 43, p.39.
% r is defined in equation 47, p.39.
% Psi is defined in equation 49, p.40.
% theta(2) uses equations 50 and 51, p.40, based on the configuration
% parameter n2
%
if sol(2) == 1
n2 = -1;
else
n2 = 1;
end
if sol(1) == 2
n2 = -n2;
end
V114 = Px*cos(theta(1)) + Py*sin(theta(1));
r = sqrt(V114^2 + Pz^2);
Psi = acos((a2^2-d4^2-a3^2+V114^2+Pz^2)/(2.0*a2*r));
if ~isreal(Psi)
theta = [];
else
theta(2) = atan2(Pz,V114) + n2*Psi;
%
% Solve for theta(3)
%
% theta(3) uses equation 57, p. 40.
%
num = cos(theta(2))*V114+sin(theta(2))*Pz-a2;
den = cos(theta(2))*Pz - sin(theta(2))*V114;
theta(3) = atan2(a3,d4) - atan2(num, den);
endikine6s的第二个参数通过字符串对“arm、elbow、wrist”方向进行配置,上述代码在计算解析解时会根据配置选择不同的公式作为解决方案。
% 'l' arm to the left (default)
% 'r' arm to the right
% 'u' elbow up (default)
% 'd' elbow down
% 'n' wrist not flipped (default)
% 'f' wrist flipped (rotated by 180 deg)ikine源文件中注释如下(已翻译):
- RTB 9.11中已完全重新实现了此功能.
- 不需要MATLAB优化工具箱.
- 解决方案是迭代计算的.
- 实现Levenberg-Marquardt可变步长求解器 .
- 公差是根据当前和所需刀具姿态之间的误差范数计算的。此规范是根据距离和角度计算的,没有任何权重。
- 运动学逆解通常不是唯一的,并且取决于初始猜测Q0(默认为0)。
- Q0的默认值为零,这对大多数操纵器(例如puma560,twolink)而言都不是一个好的选择,因为它对应于运动学奇点。
- 这样的解决方案是完全通用的,尽管比ikine6s或ikine3等象征性推导的特定逆运动学解决方案效率低得多。
- 这种方法允许以奇异性获得解决方案,但是可以随意分配零空间内的关节角度。
- 如果定义了关节偏移,则将它们添加到逆运动学中以生成Q。
- 这个解决方案不考虑关节限制。
- “搜索”选项使用从整个配置空间中选择的初始条件执行蛮力搜索。
- 如果使用“搜索”选项,则必须定义任何棱柱形接头的极限。
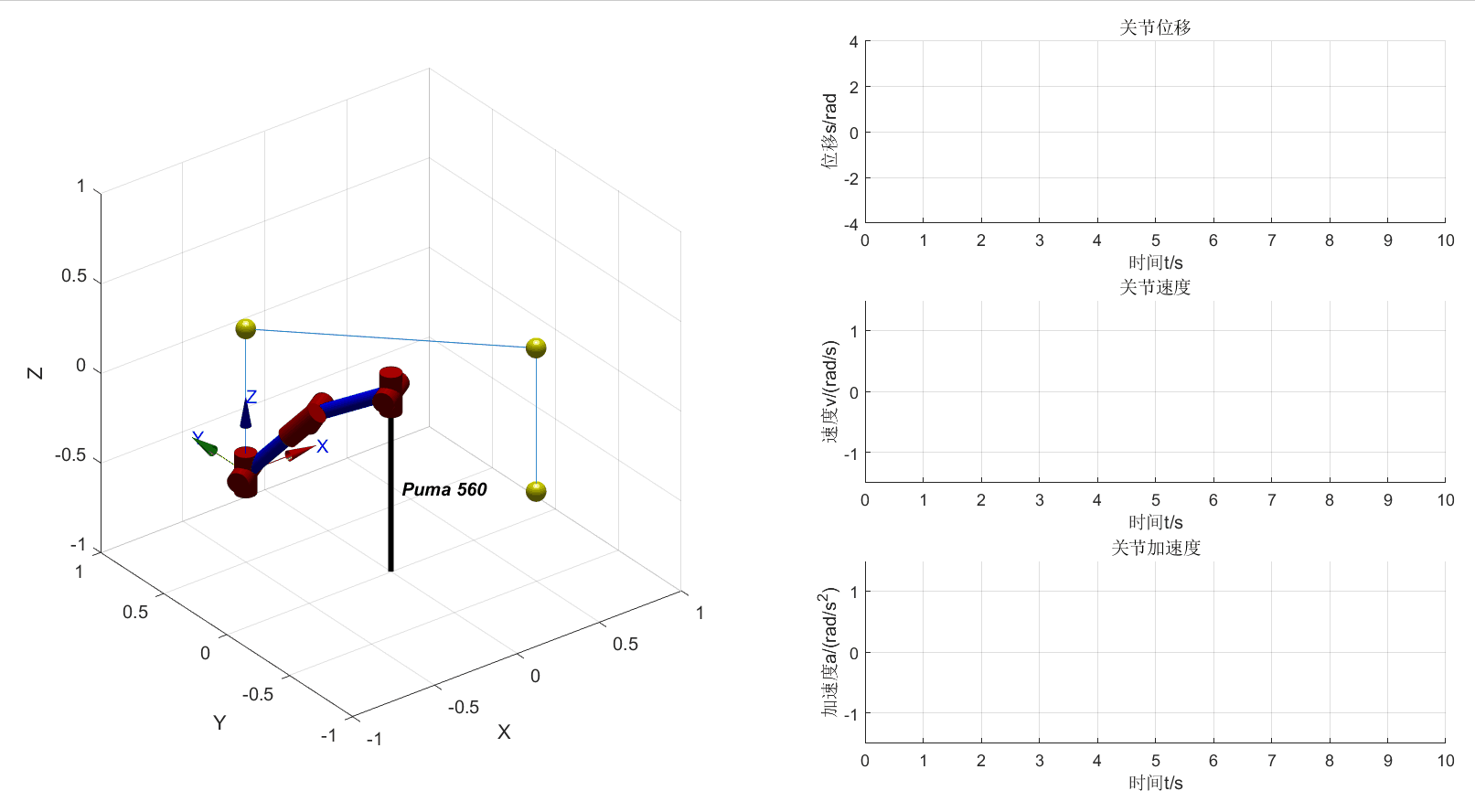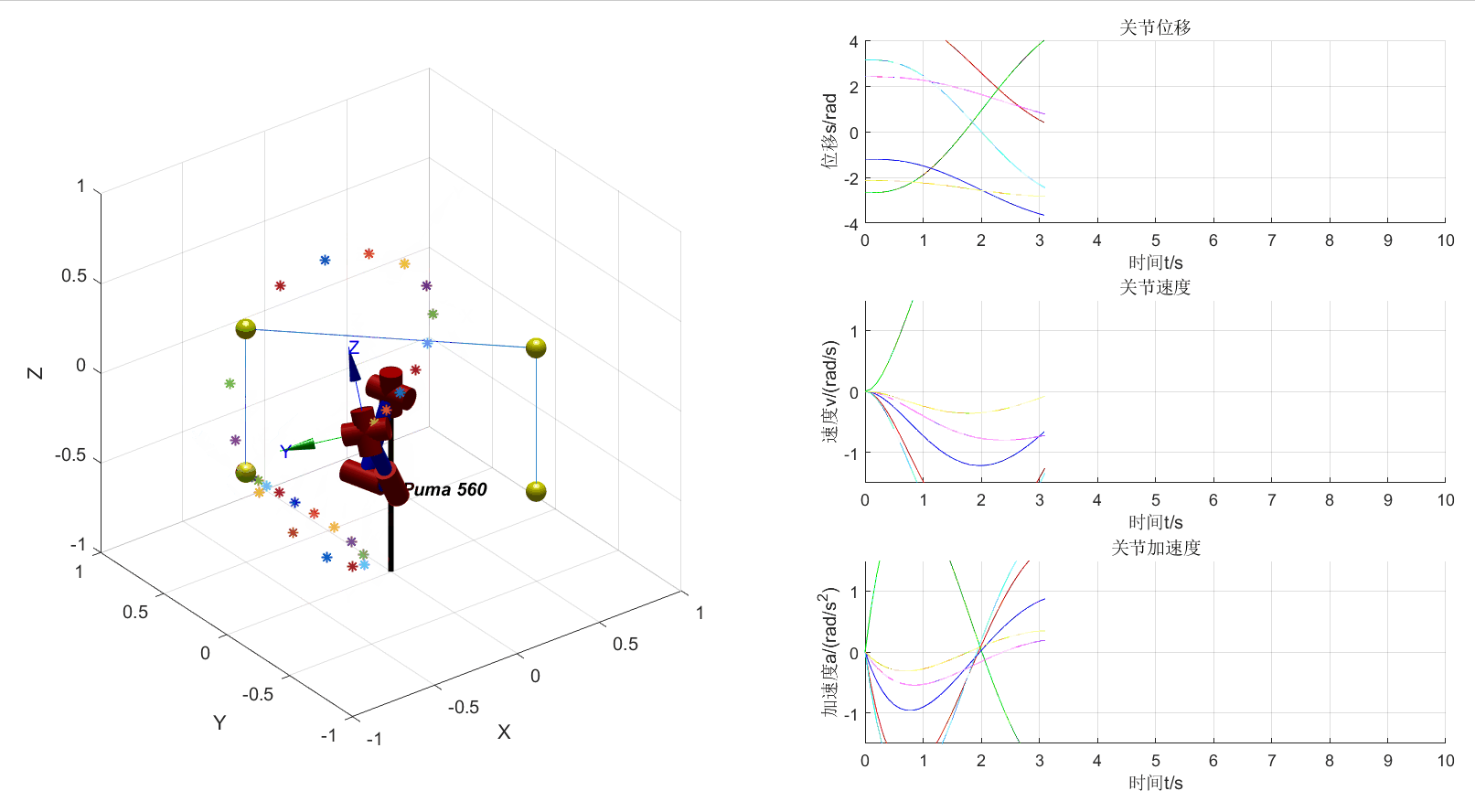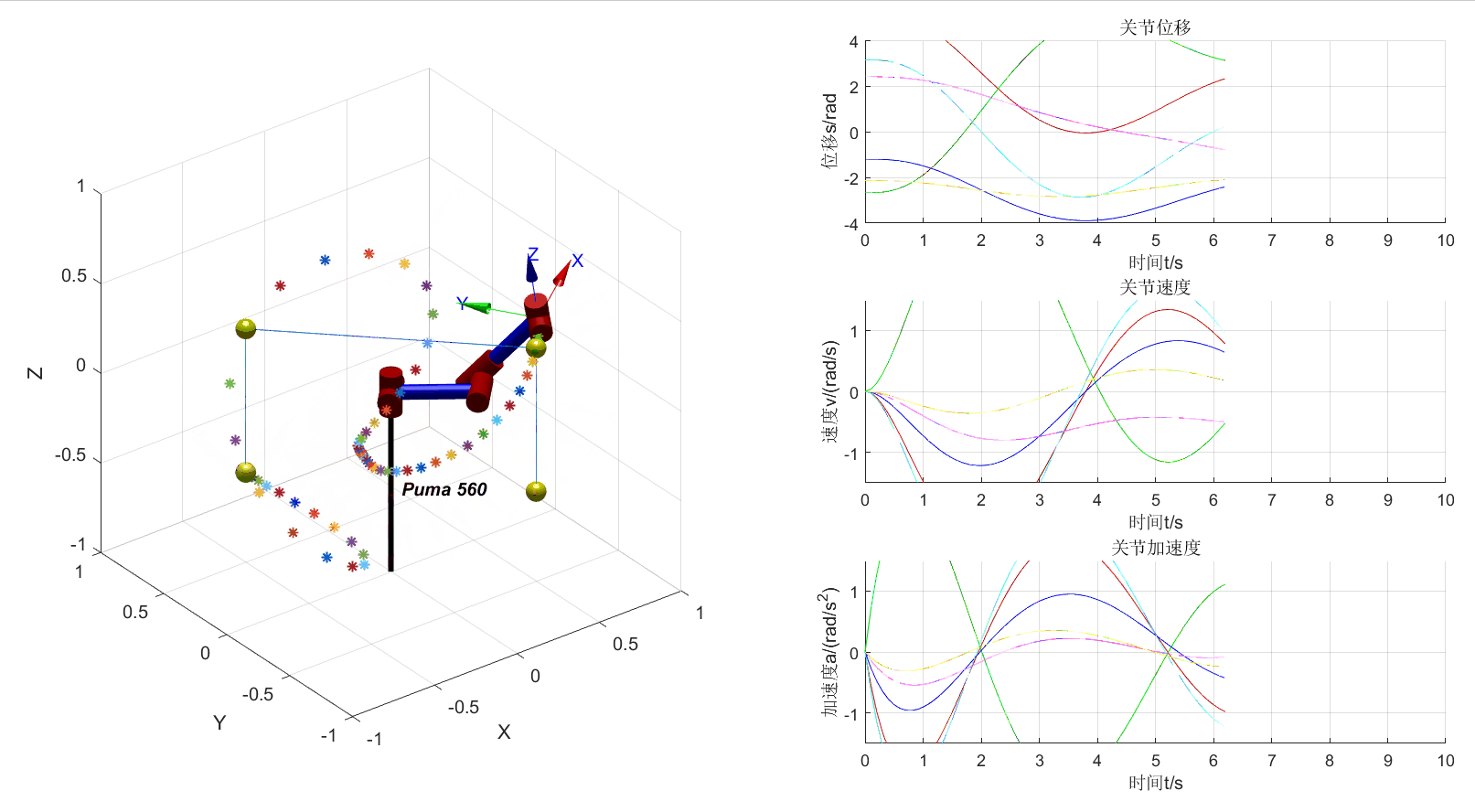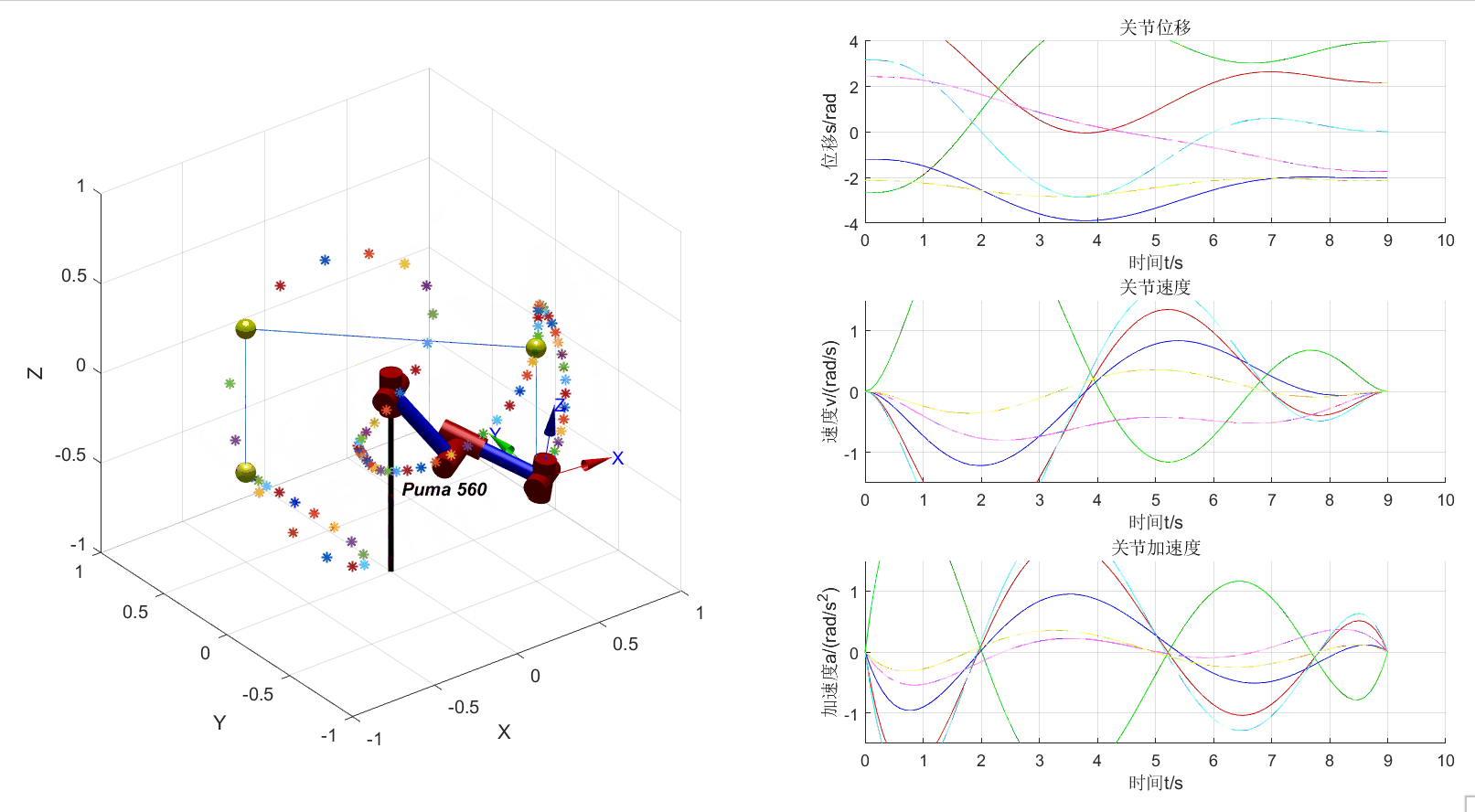
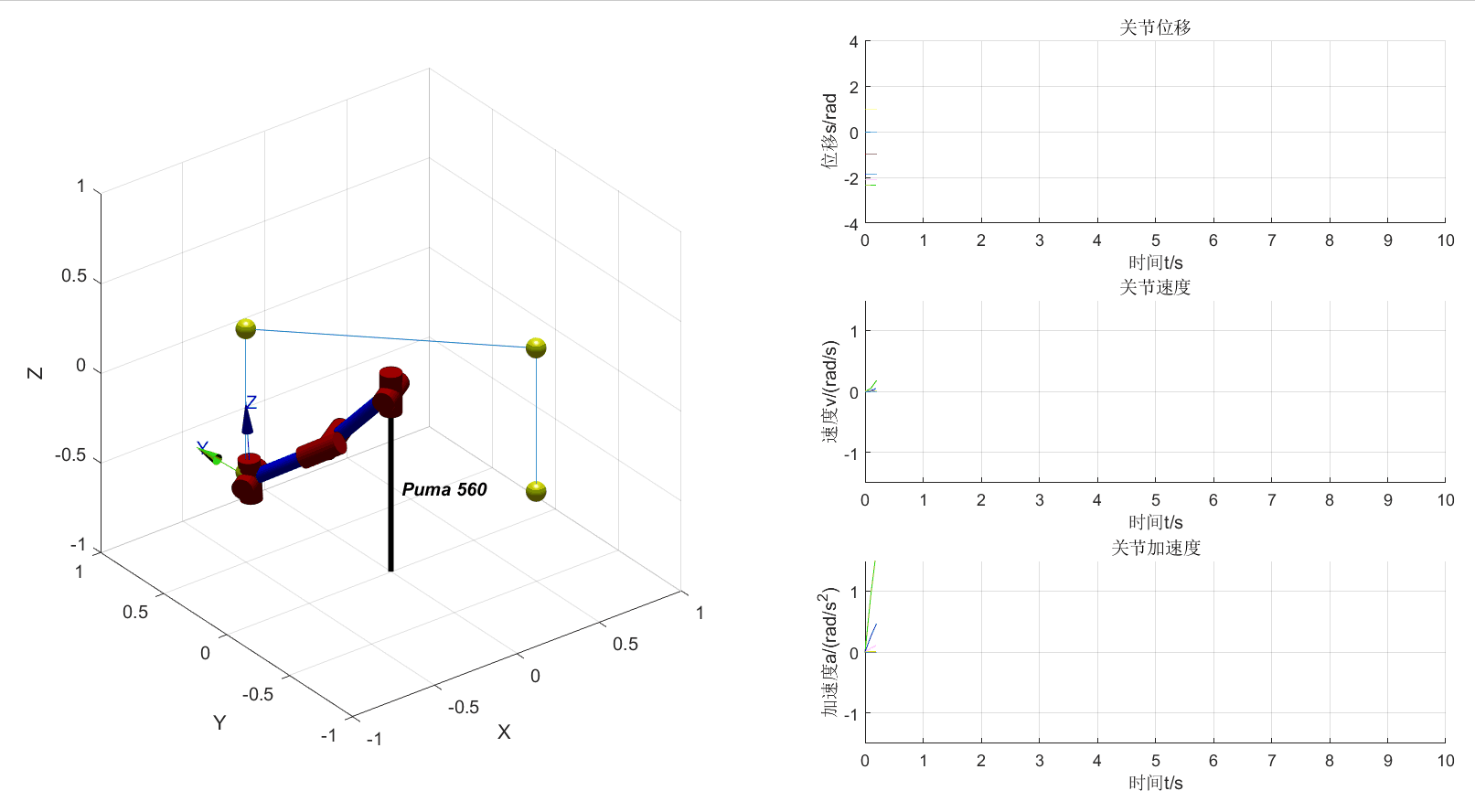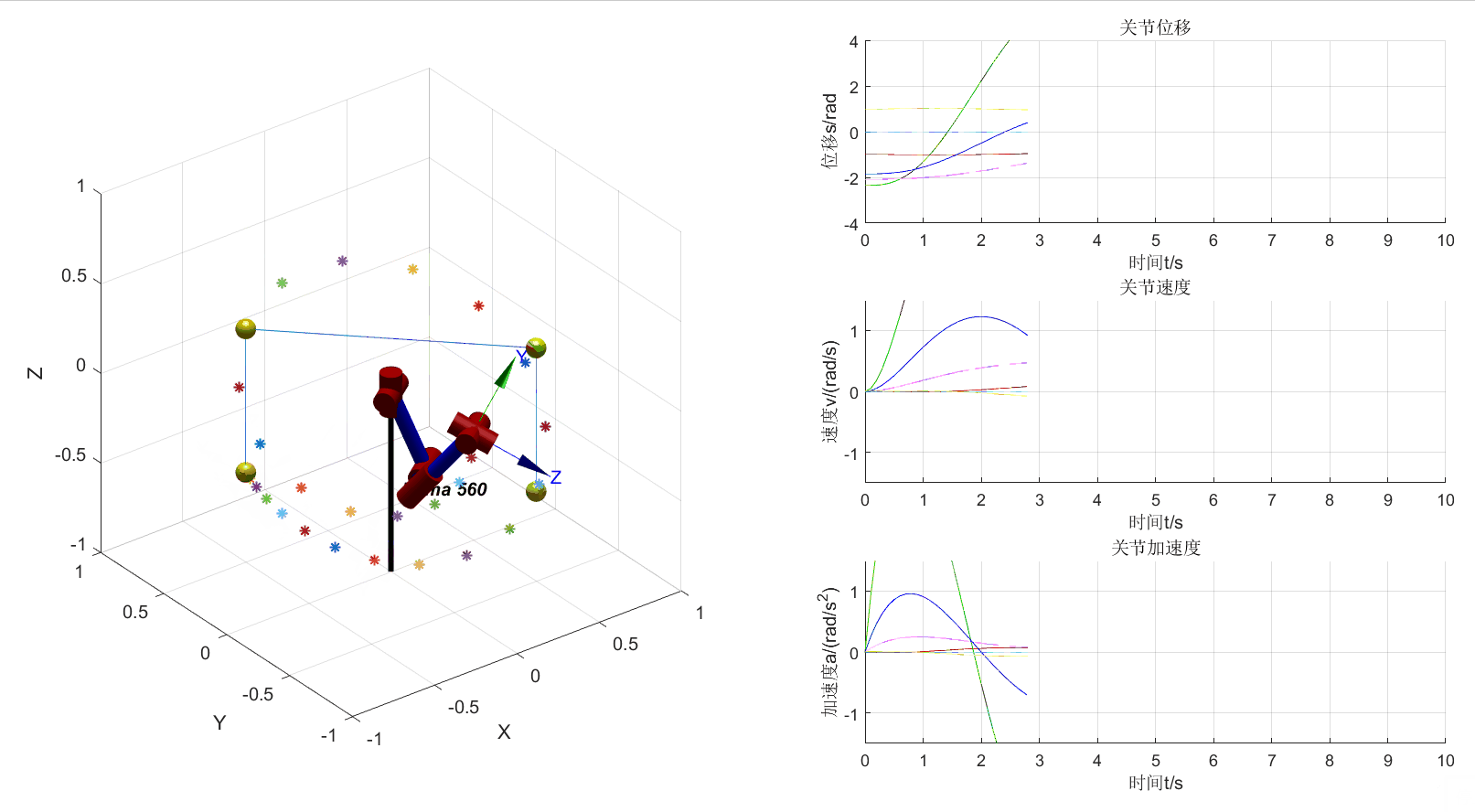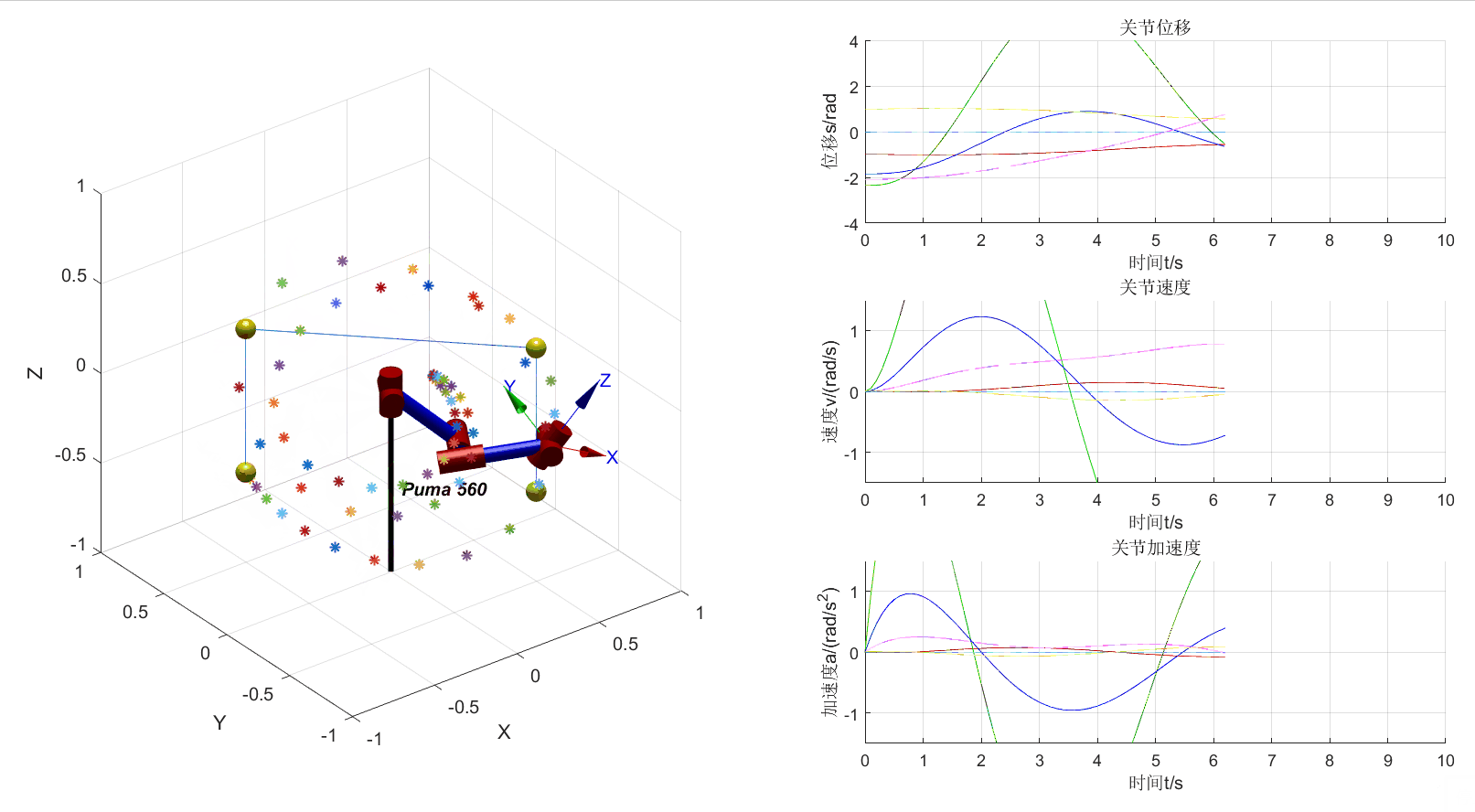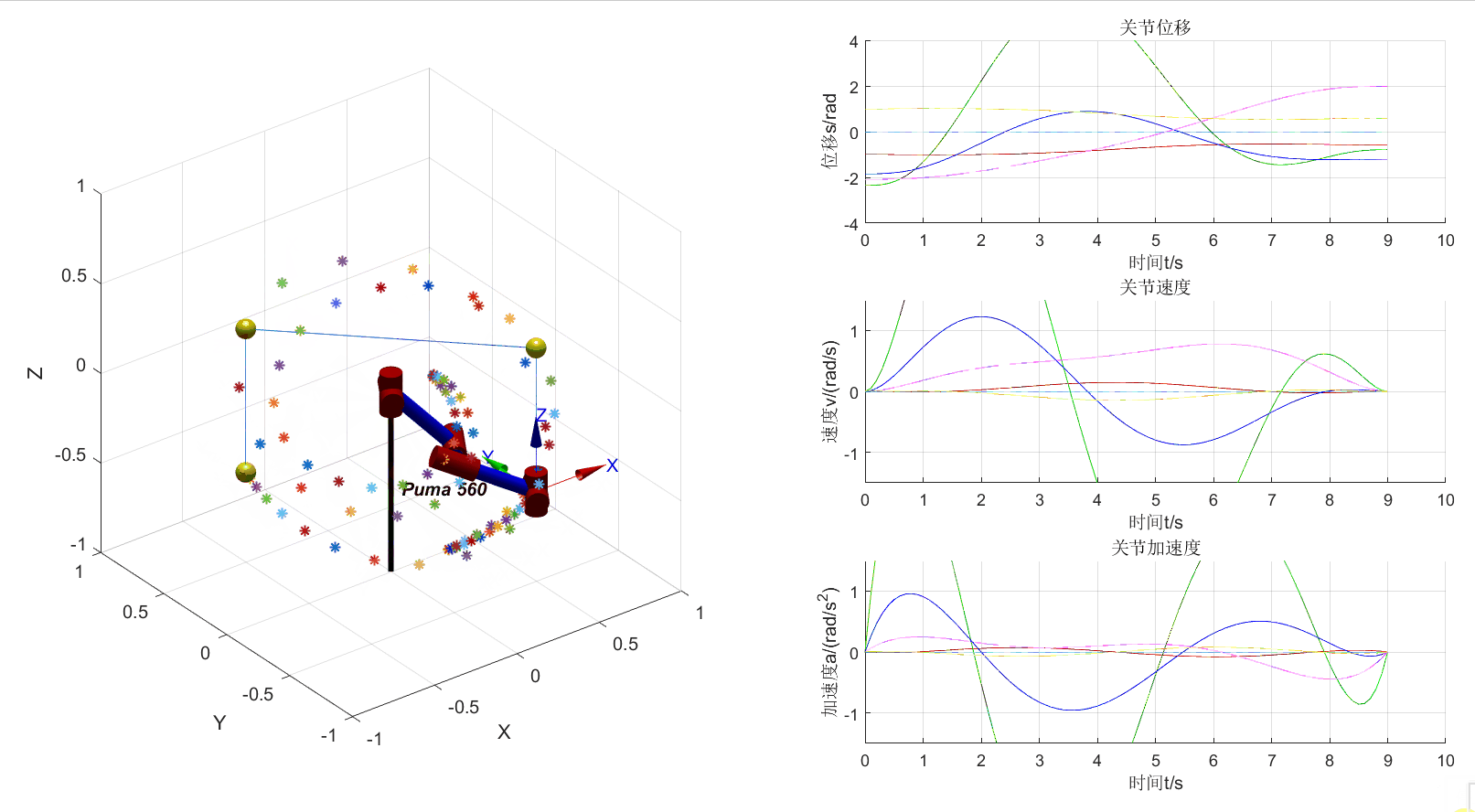
从上图可以看出机械臂运动轨迹混乱,这是由于缺少关节方向的限制导致的。
七次多项式规划的轨迹是一条不规则的曲线,七次多项式次数很高,可以很好地拟合曲线,但是在这里我们并不是去拟合轨迹曲线,而是使用插值的方法。我们的已知条件只有8个(初末位置的关节位置、速度及加速度以及两个中间点的关节位置),七次多项式有8个未知系数,通过插值方法计算出来的的曲线只能保证满足这个8个条件,而且是严格满足的,这就忽视了总体的效果。轨迹上可以取无数个点,这些点的斜率(速度)和斜率的导数(加速度)要想全部满足是不可能,如果能够引入更多的条件,使用插值方法也只能通过增加多项式的次数或将轨迹曲线分段计算来满足尽可能多的条件。 貌似插值节点取的越多,插值曲线越接近原始曲线,但事实并非如此,随着插值节点的增多,多项式的次数也在增高,插值曲线在一些区域会出现跳跃,并且越来越偏离原始曲线,这个现象被 Tolmé Runge 发现并解释。 为了解决这个问题,可以使用分段插值法。分段插值一般不会使用四次以上的多项式,而二次多项式会出现尖点,也是有问题的。所以就剩下线性和三次插值,最后使用最多的还是线性分段插值,这个好处是显而易见的。[1]
在绘制图像的时候,因为关节的位置、速度、加速度曲线是和机械臂运动同时绘制的,在for循环中绘制图例会导致速度很慢,所以演示的gif动图中有含有图例和不含图例的,含有图例的“轨迹规划(已快进).gif”运行速度过慢,应该在9s结束运动却要运行2min,最终减少了帧数,演示时长缩短,但没有缩为9s。“轨迹规划(无图例).gif”较好地将实际9s的时间考虑进去,使用pause函数根据时间步长每次进行延时绘制。 最后的代码中是先计算出轨迹保存在变量中,最后再绘制图像,以提高速度。
[1] https://www.zhihu.com/question/24276013
%% 标准DH建立puma560机器人模型
clear;
clc;
% %建立机器人模型(标准D-H参数)
% theta_dh=[-pi/2 0 -pi/2 0 0 0];
% %theta=[0 0 -pi/2 pi/2 pi/2 0];
% % theta d a alpha offset
% L1=Link([ theta_dh(1) 0 0 pi/2 0 ],'standard'); %连杆的D-H参数
% L2=Link([ theta_dh(2) 0 0.4318 0 0 ],'standard');
% L3=Link([ theta_dh(3) 0.1501 0.0203 -pi/2 0 ],'standard');
% L4=Link([ theta_dh(4) 0.4318 0 -pi/2 0 ],'standard');
% L5=Link([ theta_dh(5) 0 0 pi/2 0 ],'standard');
% L6=Link([ theta_dh(6) 0 0 0 0 ],'standard');
% robot=SerialLink([L1 L2 L3 L4 L5 L6],'name','puma560','base' , ...
% transl(0, 0, 0)* trotz(0)); %连接连杆,机器人取名puma560
% % base pose of robot's base (4x4 homog xform)
% % figure(1)
% % robot.teach() %teach可视化模型并可以单轴驱动,可以查看模型与实际机器人的关节运动是否一致。
% robot.display(); %Link 类函数,显示建立的机器人DH参数
mdl_puma560
%% 求解轨迹中间点的关节角
% 左臂、手肘朝下、手腕翻转(旋转180度)
pos0 = [-0.5,0.5,-0.5]; % 起始位置(取点)
pos1 = [-0.5,0.5,0.3]; % 转移位置(抬起或离开点)
pos2 = [0.5,-0.5,0.3]; % 卸下位置(下降点)
posf = [0.5,-0.5,-0.5]; % 目标位置(放置点)
pos = [pos0;pos1;pos2;posf];
% 转换为齐次矩阵
T0 = transl(pos0);
T1 = transl(pos1);
T2 = transl(pos2);
Tf = transl(posf);
% 求解关节角
theta_0 = p560.ikine6s(T0,'rdf');
theta_1 = p560.ikine6s(T1,'rdf');
theta_2 = p560.ikine6s(T2,'rdf');
theta_f = p560.ikine6s(Tf,'rdf');
disp("起始位置的关节角:");
disp(theta_0)
disp("转移位置的关节角:");
disp(theta_1)
disp("卸下位置的关节角:");
disp(theta_2);
disp("目标位置的关节角:");
disp(theta_f);
%% 求解七次多项式系数
% 3段时间(单位:秒)
t0 = 0; % 抬起开始时刻
t1 = 2; % 抬起结束时刻
t2 = t1 + 4; % 平移结束时刻
tf = t2 + 3; % 下降结束时刻
% 6个关节的初始条件
theta_0_ = [0 0 0 0 0 0]; % 初始位置速度
theta_0__ = [0 0 0 0 0 0]; % 初始位置加速度
theta_f_ = [0 0 0 0 0 0]; % 目标位置速度
theta_f__ = [0 0 0 0 0 0]; % 目标位置加速度
THETA = [theta_0;theta_0_;theta_0__;theta_1;theta_2;theta_f;theta_f_;theta_f__];
M =...
[1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 2 0 0 0 0 0
1 t1 t1^2 t1^3 t1^4 t1^5 t1^6 t1^7
1 t2 t2^2 t2^3 t2^4 t2^5 t2^6 t2^7
1 tf tf^2 tf^3 tf^4 tf^5 tf^6 tf^7
0 1 2*tf 3*tf^2 4*tf^3 5*tf^4 6*tf^5 7*tf^6
0 0 2 6*tf 12*tf^2 20*tf^3 30*tf^4 42*tf^5];
C = M^-1 * THETA;
disp("6个关节各自的七次多项式的系数为(从左到右为第1~6个关节):");
disp(C);
dt = 0.1; % 时间步长
t = [-dt;0];
figure(2)
set(gcf,'outerposition',get(0,'screensize'),'color','w');
subplot(3,2,[1,3,5]);
axis([-1 1 -1 1 -1 1]);
hold on
plot3(pos(:,1),pos(:,2),pos(:,3));
plot_sphere(pos', 0.05, 'y');
subplot(3,2,2);
axis([0 10 -4 4]);
hold on
title('关节位移');
xlabel('时间t/s');
ylabel('位移s/rad');
grid on
% plot(t,[0;0],'-r',t,[0;0],'-g',t,[0;0],'-b',t,[0;0],'-c',t,[0;0],'-m',t,[0;0],'-y','MarkerSize',15);
% legend('关节1','关节2','关节3','关节4','关节5','关节6','Location','eastoutside');
subplot(3,2,4);
axis([0 10 -1.5 1.5]);
hold on
title('关节速度');
xlabel('时间t/s');
ylabel('速度v/(rad/s)');
grid on
subplot(3,2,6);
axis([0 10 -1.5 1.5]);
hold on
title('关节加速度');
xlabel('时间t/s');
ylabel('加速度a/(rad/s^2)');
grid on
[~, count] = size(0:dt:tf);
q3 = zeros(2,6,count);
v3 = zeros(2,6,count);
a3 = zeros(2,6,count);
T_2 = zeros(3,count);
k=1;
for i = 0:dt:tf
q = [ones(2,1) t t.^2 t.^3 t.^4 t.^5 t.^6 t.^7] * C; % 关节位移
v = [zeros(2,1) ones(2,1) 2*t 3*t.^2 4*t.^3 5*t.^4 6*t.^5 7*t.^6] * C; % 速度
a = [zeros(2,1) zeros(2,1) 2*ones(2,1) 6*t 12*t.^2 20*t.^3 30*t.^4 42*t.^5] * C; % 加速度
q3(:,:,k) = q; % 保存数据
v3(:,:,k) = v; % 保存数据
a3(:,:,k) = a; % 保存数据
T_ = p560.fkine(q(2,:)); % 正运动学求解
T_2(:,k) = T_.t; % 保存数据
k=k+1;
t = t + dt;
end
k=1;
t = [-dt;0];
for i = 0:dt:tf
subplot(3,2,[1,3,5])
plot3(T_2(1,k),T_2(2,k),T_2(3,k),'*','LineWidth',1); % 在三维视图中绘制出运动轨迹
hold on
p560.plot(q3(2,:,k));%动画演示
qq = q3(:,:,k)';
vv = v3(:,:,k)';
aa = a3(:,:,k)';
subplot(3,2,2);
plot(t,qq(1,:),'-r',t,qq(2,:),'-g',t,qq(3,:),'-b',t,qq(4,:),'-c',t,qq(5,:),'-m',t,qq(6,:),'-y','MarkerSize',15);
legend('关节1','关节2','关节3','关节4','关节5','关节6','Location','eastoutside');
subplot(3,2,4);
plot(t,vv(1,:),'-r',t,vv(2,:),'-g',t,vv(3,:),'-b',t,vv(4,:),'-c',t,vv(5,:),'-m',t,vv(6,:),'-y','MarkerSize',15);
legend('关节1','关节2','关节3','关节4','关节5','关节6','Location','eastoutside');
subplot(3,2,6);
plot(t,aa(1,:),'-r',t,aa(2,:),'-g',t,aa(3,:),'-b',t,aa(4,:),'-c',t,aa(5,:),'-m',t,aa(6,:),'-y','MarkerSize',15);
legend('关节1','关节2','关节3','关节4','关节5','关节6','Location','eastoutside');
t = t + dt;
k = k + 1;
end