-
Notifications
You must be signed in to change notification settings - Fork 247
[KratosAPI] MultiPoint Constraint (MPC) interface
MultiFreedom Constraints (MFC) are functional equations that connect two or more degrees of freedom components:
F(nodal degree of freedom) = prescribed value
An MFC of this form is called multipoint or multinode (MPC) if it involves DoF components at different nodes. The constraint is called linear if all displacement components appear linearly on the left-hand-side, and nonlinear otherwise.
There are basically three methods for treating MFC.
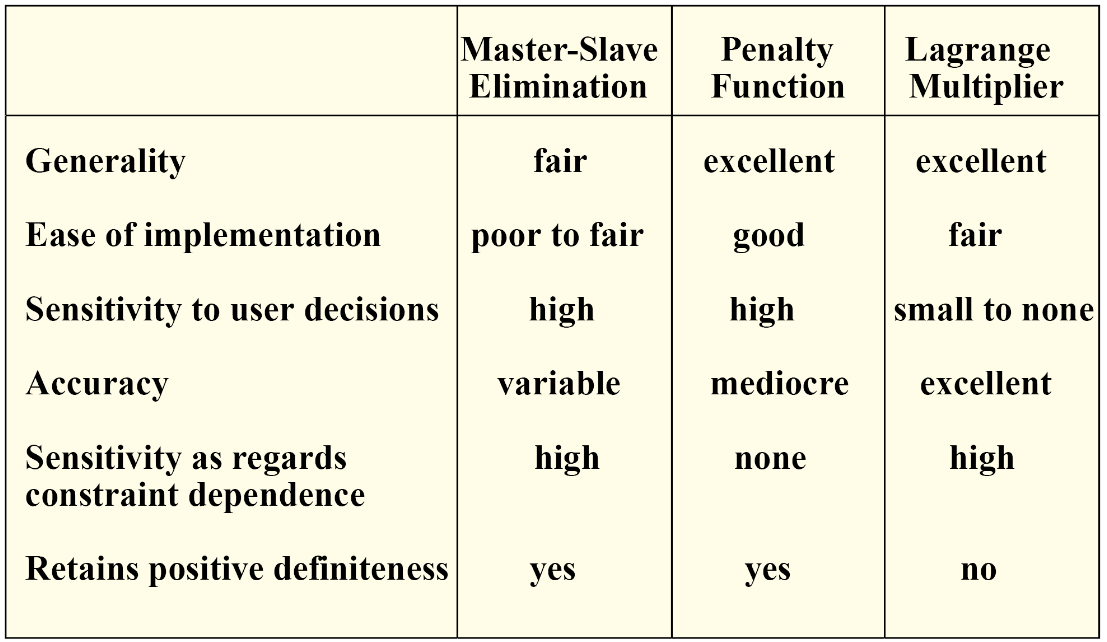
- Master-Slave Elimination. The degrees of freedom involved in each MFC are separated into master and slave freedoms. The slave freedoms are then explicitly eliminated. The modified equations do not contain the slave freedoms.
- Penalty Augmentation. Also called the penalty function method. Each MFC is viewed as the presence of a fictitious elastic structural element called penalty element that enforces it approximately. This element is parametrized by a numerical weight. The exact constraint is recovered if the weight goes to infinity. The MFCs are imposed by augmenting the finite element model with the penalty elements.
- Lagrange Multiplier Adjunction. For each MFC an additional unknown is adjoined to the master stiffness equations. Physically this set of unknowns represent constraint forces that would enforce the constraints exactly should they be applied to the unconstrained system.
These methods can be compared, the following table resumes the differences between them.
The MFC implemented in Kratos is the Master-Slave Elimination, this will be the one presented in the Formulation section.
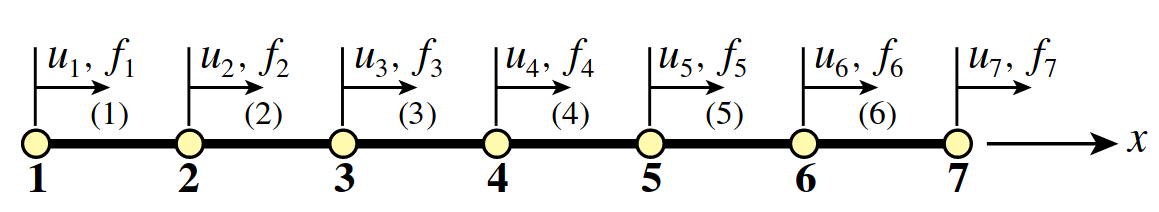
We will use a very simple structure example in order to explain how the formulation works. This structure consists of six bar elements connected by seven nodes that can only displace in the x direction. Before imposing various multifreedom constraints discussed below, the master stiffness equations for this problem are assumed to be
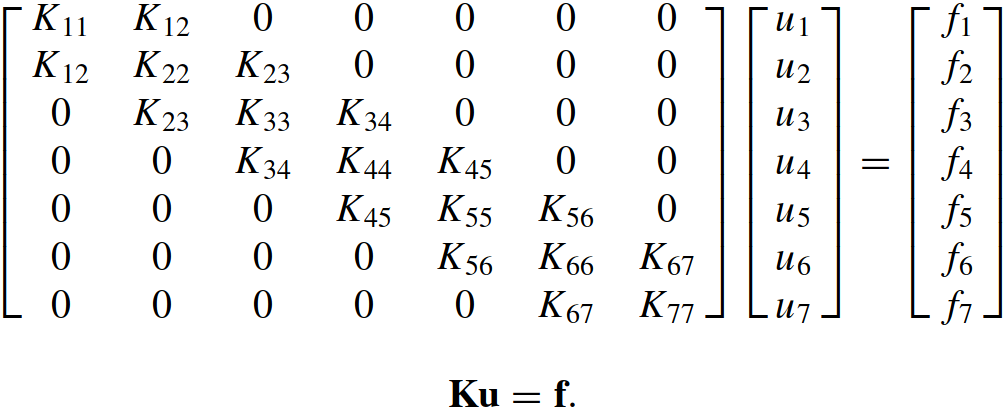
Now let us specify a multifreedom constraint that states that nodes 2 and 6 are to move by the same amount:
u2 = u6
Passing all node displacements to the right hand side gives the canonical form:
u2-u6=0
Constraintconditionsofthistypearesometimescalled rigid links becausetheycanbemechanically interpreted as forcing node points 2 and 6 to move together as if they were tied by a rigid member.
To apply this method by hand, the MFCs are taken one at a time. For each constraint a slave degree of freedom is chosen. The freedoms remaining in that constraint are labeled master. A new set of degrees of freedom u is established by removing all slave freedoms from u. This new vector contains master freedoms as well as those that do not appear in the MFCs. A matrix transformation equation that relates u to u is generated. This equation is used to apply a congruential transformation to the master stiffness equations. This procedure yields a set of modified stiffness equations that are expressed in terms of the new freedom set u. Because the modified system does not contain the slave freedoms, these have been effectively eliminated.
The mechanics of the process is best seen by going through an example.
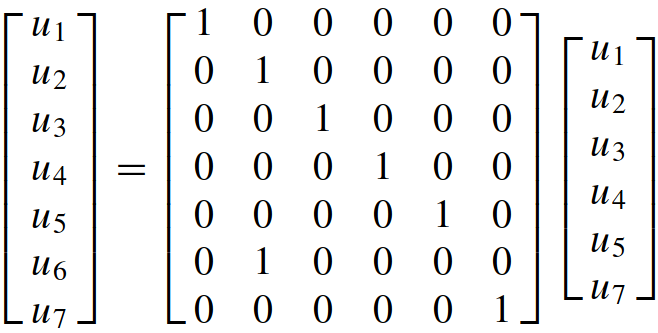
This is the required transformation relation. In compact form:
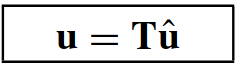
Replacing and premultiplying by T yields the modified system:
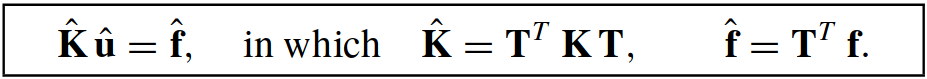
Carrying out the indicated matrix multiplications yields:
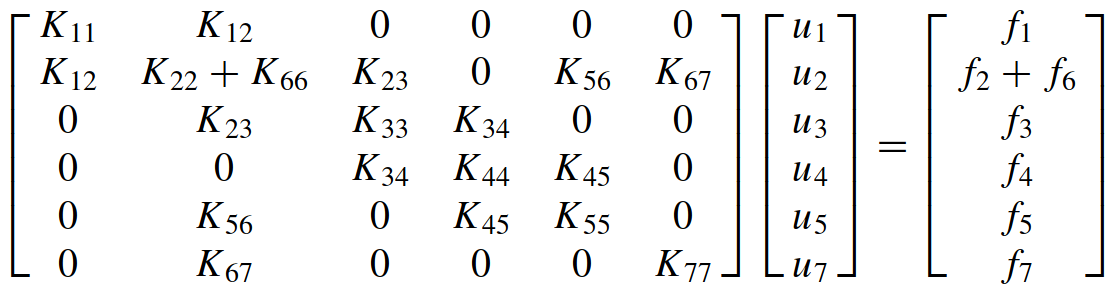
The MPC are implemented in Kratos via the MasterSlaveConstraint class, and particularly the linear kinematic relationship can be found in in the class LinearMasterSlaveConstraint class.
The LinearMasterSlaveConstraint is defined by the following:
- Index: The Id of the new created constraint
- Vector of master DoF: The vector containing the DoF of the master side
- Vector of slave DoF: The vector containing the DoF of the slave side
- A relation matrix : The relation matrix between the master/slave DoF. This is T in the theoretical formulation.
- A constant vector: The vector containing the additional kinematic relationship
Additionally to this, in order to consider the MPC into ths system assembly the ResidualBasedBlockBuilderAndSolverWithConstraints must be used as builder and solver.
The MasterSlaveConstraint are part of the Mesh class, so they are stored in the ModelPart as the elements and conditions do. Then the ModelPart has an interface to access and create them. Particularly the methods CreateNewMasterSlaveConstraint are of interest, there are three options:
MasterSlaveConstraint::Pointer CreateNewMasterSlaveConstraint(
const std::string& ConstraintName,
IndexType Id,
DofsVectorType& rMasterDofsVector,
DofsVectorType& rSlaveDofsVector,
const MatrixType& RelationMatrix,
const VectorType& ConstantVector,
IndexType ThisIndex = 0);
MasterSlaveConstraint::Pointer CreateNewMasterSlaveConstraint(
const std::string& ConstraintName,
IndexType Id,
NodeType& rMasterNode,
const DoubleVariableType& rMasterVariable,
NodeType& rSlaveNode,
const DoubleVariableType& rSlaveVariable,
const double Weight,
const double Constant,
IndexType ThisIndex = 0);
MasterSlaveConstraint::Pointer CreateNewMasterSlaveConstraint(
const std::string& ConstraintName,
IndexType Id,
NodeType& rMasterNode,
const VariableComponentType& rMasterVariable,
NodeType& rSlaveNode,
const VariableComponentType& rSlaveVariable,
double Weight,
double Constant,
IndexType ThisIndex = 0);This can be seen in a simple example:
import KratosMultiphysics
# Define a Model
current_model = KratosMultiphysics.Model()
mp = current_model.CreateModelPart("Main")
mp.AddNodalSolutionStepVariable(KratosMultiphysics.DISPLACEMENT)
mp.AddNodalSolutionStepVariable(KratosMultiphysics.REACTION)
mp.CreateNewNode(1, 0.00000, 0.00000, 0.00000)
mp.CreateNewNode(2, 0.00000, 1.00000, 0.00000)
KratosMultiphysics.VariableUtils().AddDof(KratosMultiphysics.DISPLACEMENT_X, KratosMultiphysics.REACTION_X, mp)
KratosMultiphysics.VariableUtils().AddDof(KratosMultiphysics.DISPLACEMENT_Y, KratosMultiphysics.REACTION_Y, mp)
KratosMultiphysics.VariableUtils().AddDof(KratosMultiphysics.DISPLACEMENT_Z, KratosMultiphysics.REACTION_Z, mp)
mp.CreateNewMasterSlaveConstraint("LinearMasterSlaveConstraint", 1, mp.Nodes[1], KratosMultiphysics.DISPLACEMENT_X, mp.Nodes[2], KratosMultiphysics.DISPLACEMENT_X, 1.0, 0)
# We impose the BC
mp.Nodes[1].Fix(KratosMultiphysics.DISPLACEMENT_X)
mp.Nodes[1].SetSolutionStepValue(KratosMultiphysics.DISPLACEMENT_X, 0.1)
#define a minimal newton raphson solver
linear_solver = KratosMultiphysics.SkylineLUFactorizationSolver()
builder_and_solver = KratosMultiphysics.ResidualBasedBlockBuilderAndSolverWithConstraints(linear_solver)
scheme = KratosMultiphysics.ResidualBasedIncrementalUpdateStaticScheme()
convergence_criterion = KratosMultiphysics.ResidualCriteria(1e-10, 1e-12)
convergence_criterion.SetEchoLevel(0)
max_iters = 100
compute_reactions = False
reform_step_dofs = True
move_mesh_flag = False
strategy = KratosMultiphysics.ResidualBasedNewtonRaphsonStrategy(
mp, scheme, linear_solver, convergence_criterion,
builder_and_solver, max_iters, compute_reactions,
reform_step_dofs, move_mesh_flag)
strategy.SetEchoLevel(0)
strategy.Initialize()
strategy.Check()
strategy.Solve()
print(mp.Nodes[2].GetSolutionStepValue(KratosMultiphysics.DISPLACEMENT_X))
assert mp.Nodes[2].GetSolutionStepValue(KratosMultiphysics.DISPLACEMENT_X) == mp.Nodes[1].GetSolutionStepValue(KratosMultiphysics.DISPLACEMENT_X)IMPORTANT: The slaves nodes must have the flag SLAVE set to true
In this section a brief tutorial of "How To" create an example is explained.
In order to generate the required input data files we use the geometry pre and post processor GiD (https://www.gidhome.com/download/official-versions). Additionally we need to download the KratosMultiphysics GiD interface (https://github.com/KratosMultiphysics/GiDInterface - > download .zip). Once we open the GiD software we must load the Kratos problem type by:

And then select the StructuralMechanicsApplication as:

And then we select 3D for this particular case:

Then a new menu will appear on the left with all the options available.

Now we have generated an arbitrary geometry like the one below.

[1] "MultiFreedom Constraint I " by C. Felippa. Link
[2] "MultiFreedom Constraint II " by C. Felippa. Link
[3] "Multi-Point Constraints". Link
- Getting Kratos (Last compiled Release)
- Compiling Kratos
- Running an example from GiD
- Kratos input files and I/O
- Data management
- Solving strategies
- Manipulating solution values
- Multiphysics
- Video tutorials
- Style Guide
- Authorship of Kratos files
- Configure .gitignore
- How to configure clang-format
- How to use smart pointer in Kratos
- How to define adjoint elements and response functions
- Visibility and Exposure
- Namespaces and Static Classes
Kratos structure
Conventions
Solvers
Debugging, profiling and testing
- Compiling Kratos in debug mode
- Debugging Kratos using GDB
- Cross-debugging Kratos under Windows
- Debugging Kratos C++ under Windows
- Checking memory usage with Valgind
- Profiling Kratos with MAQAO
- Creating unitary tests
- Using ThreadSanitizer to detect OMP data race bugs
- Debugging Memory with ASAN
HOW TOs
- How to create applications
- Python Tutorials
- Kratos For Dummies (I)
- List of classes and variables accessible via python
- How to use Logger
- How to Create a New Application using cmake
- How to write a JSON configuration file
- How to Access DataBase
- How to use quaternions in Kratos
- How to do Mapping between nonmatching meshes
- How to use Clang-Tidy to automatically correct code
- How to use the Constitutive Law class
- How to use Serialization
- How to use GlobalPointerCommunicator
- How to use PointerMapCommunicator
- How to use the Geometry
- How to use processes for BCs
- How to use Parallel Utilities in futureproofing the code
- Porting to Pybind11 (LEGACY CODE)
- Porting to AMatrix
- How to use Cotire
- Applications: Python-modules
- How to run multiple cases using PyCOMPSs
- How to apply a function to a list of variables
- How to use Kratos Native sparse linear algebra
Utilities
Kratos API
Kratos Structural Mechanics API