Merge pull request #85 from Emisaber/main

hai

blogs/通识课/python常用库.md

@@ -0,0 +1,216 @@
+# python常用库
+
+在import导入库之前，需要在cmd命令行执行：conda activate name_of_environment，切换到目标conda 环境中执行：pip install 库名称
+
+库函数的使用方法是（假设库的名称是name）name.函数名(a1, a2, a3)
+a1,a2,a3是函数传入的参数，python的库函数传参逻辑是库函数会定义很多的参数方法，其中大部分参数可以默认（不用在代码里面指定），只有关键的参数才会需要我们输入
+
+> 尝试搜索`matplotlib.pyplot`这个库的库函数之一：plot(x, y) 
+下面是这个库的官方网站
+https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html
+下面是中文简单版教程
+https://www.runoob.com/matplotlib/matplotlib-pyplot.html
+> 
+
+> 画单条线：plot([x], y, [fmt], *, data=None, **kwargs)
+画多条线：plot([x], y, [fmt], [x2], y2, [fmt2], ..., **kwargs)
+> 
+
+![image.png](https://raw.githubusercontent.com/Emisaber/pic_obsidian/main/image.png)
+
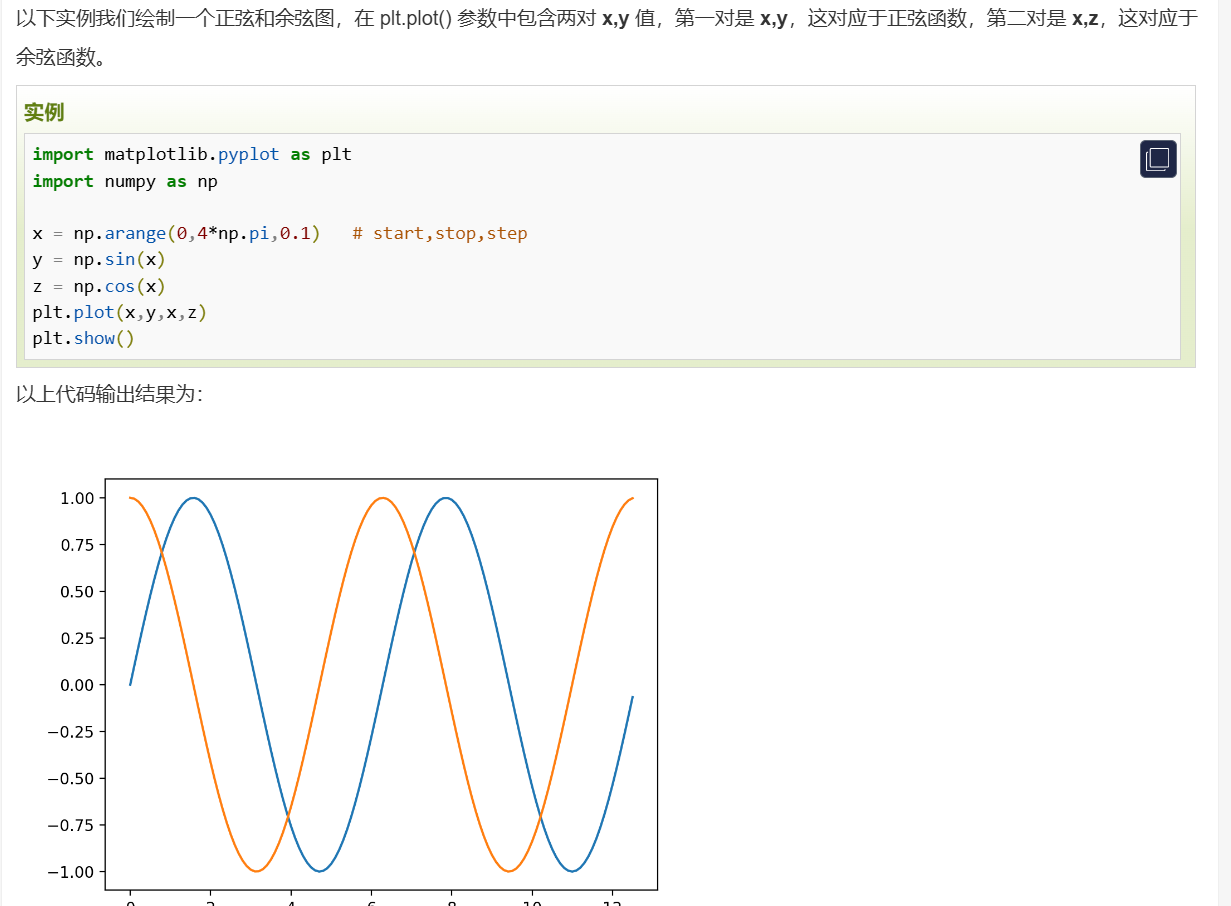+### math库和turtle库
+
+```python
+import math
+from turtle import *
+
+def hearta(k):
+    return 15 * math.sin(k) ** 3
+def heartb(k):
+    return 12 * math.cos(k) - 5 * \
+           math.cos(2 * k) - 2 * \
+           math.cos(4 * k)
+
+speed(10)
+bgcolor("white")
+for i in range(100000):
+    goto(hearta(i) * 20, heartb(i) * 20)
+    for j in range(5):
+        color("#f73487")
+        pensize(5) 
+    goto(0, 0)
+```
+
+`import math`：导入Python的math库，用于数学计算
+
+`from turtle import *`：从turtle库中导入所有函数和变量
+
+- `def hearta(k):`：定义一个函数`hearta`，用于计算爱心的x坐标
+
+    `return 15 * math.sin(k) ** 3`：返回x坐标，使用正弦函数和k的立方
+
+- `def heartb(k):`：定义一个函数`heartb`，用于计算爱心的y坐标
+
+    `return 12 * math.cos(k) - 5 * math.cos(2 * k) - 2 * math.cos(4 * k)`：返回y坐标，使用余弦函数和k的倍数。
+
+- `bgcolor("black")`：设置turtle的背景颜色为黑色
+- `for i in range(100000):`：开始一个循环，循环100000次
+    - `goto(hearta(i) * 20, heartb(i) * 20)`：移动turtle到计算出的坐标位置。
+    - `for j in range(5):`：开始一个内循环，循环5次
+
+        `color("#f73487")`：设置turtle的颜色为红色
+
+    - `goto(0, 0)`：移动turtle回到原点
+
+试一下：把pensize改成50、把speed变成30……
+
+著名的樱花树
+
+```python
+from turtle import *
+from random import *
+from math import *
+class Tree:
+    def __init__(self):
+        setup(1000, 700)
+        bgcolor(1, 1, 1)  # 背景色
+        # ht()  # 隐藏turtle
+        speed(10)  # 速度 1-10渐进，0 最快
+        # tracer(1, 100)    # 设置绘图屏幕刷新频率，参数1设置在正常刷新频次的第参数1次刷新，参数2设置每次刷新的时延
+        tracer(0, 0)
+        pu()  # 抬笔
+        backward(100)
+        # 保证笔触箭头方向始终不向下，此处使其左转90度，而不是右转
+        left(90)  # 左转90度
+        backward(300)  # 后退300
+    def tree(self, n, l):
+        pd()  # 下笔
+        # 阴影效果
+        t = cos(radians(heading() + 45)) / 8 + 0.25
+        pencolor(t, t, t)
+        pensize(n / 1.2)
+        forward(l)  # 画树枝
+        if n > 0:
+            b = random() * 15 + 10  # 右分支偏转角度
+            c = random() * 15 + 10  # 左分支偏转角度
+            d = l * (random() * 0.25 + 0.7)  # 下一个分支的长度
+            # 右转一定角度,画右分支
+            right(b)
+            self.tree(n - 1, d)
+            # 左转一定角度，画左分支
+            left(b + c)
+            self.tree(n - 1, d)
+            # 转回来
+            right(c)
+        else:
+            # 画叶子
+            right(90)
+            n = cos(radians(heading() - 45)) / 4 + 0.5
+            pencolor(n, n * 0.8, n * 0.8)
+            fillcolor(n, n * 0.8, n * 0.8)
+            begin_fill()
+            circle(3)
+            left(90)
+            end_fill()
+            # 添加0.3倍的飘落叶子
+            if random() > 0.7:
+                pu()
+                # 飘落
+                t = heading()
+                an = -40 + random() * 40
+                setheading(an)
+                dis = int(800 * random() * 0.5 + 400 * random() * 0.3 + 200 * random() * 0.2)
+                forward(dis)
+                setheading(t)
+                # 画叶子
+                pd()
+                right(90)
+                n = cos(radians(heading() - 45)) / 4 + 0.5
+                pencolor(n * 0.5 + 0.5, 0.4 + n * 0.4, 0.4 + n * 0.4)
+                fillcolor(n, n * 0.8, n * 0.8)
+                begin_fill()
+                circle(2)
+                left(90)
+                end_fill()
+                pu()
+                # 返回
+                t = heading()
+                setheading(an)
+                backward(dis)
+                setheading(t)
+                # pass
+        pu()
+        backward(l)  # 退回
+def main():
+    tree = Tree()
+    tree.tree(12, 100)  # 递归7层
+    done()
+if __name__ == '__main__':
+    main()
+```
+
+### matplotlib库
+
+```python
+import numpy as np
+import matplotlib.pyplot as plt
+
+x = np.array([1, 2, 3, 4])
+y = np.array([1, 4, 9, 16])
+
+plt.title("RUNOOB grid() Test")
+plt.xlabel("x - label")
+plt.ylabel("y - label")
+plt.plot(x, y)
+plt.grid() # 生成网格
+plt.show()
+```
+
+[Matplotlib 网格线 | 菜鸟教程 (runoob.com)](https://www.runoob.com/matplotlib/matplotlib-grid.html)
+
+```python
+import random
+import matplotlib.pyplot as plt
+
+# 设置随机点的数量
+num_points = 10000
+
+points_inside_circle = 0
+points_total = 0
+x_list, y_list, colors = [], [], []
+
+# 生成随机点并检查是否在圆内
+for _ in range(num_points):
+    x = random.uniform(-1, 1)
+    y = random.uniform(-1, 1)
+    if x**2 + y**2 <= 1:
+        points_inside_circle += 1
+        colors.append('g')  # 圆内点为绿色
+    else:
+        colors.append('b')  # 圆外点为蓝色
+    points_total += 1
+    x_list.append(x)
+    y_list.append(y)
+
+# 计算π的估计值
+pi_estimate = 4 * points_inside_circle / points_total
+print(f"估计的π值: {pi_estimate}")
+
+# 绘图
+plt.figure(figsize=(5, 5))
+plt.xlim(-1, 1)
+plt.ylim(-1, 1)
+plt.scatter(x_list, y_list, s=8, c=colors, marker='o')
+circle = plt.Circle((0, 0), 1, color='r', fill=False)
+plt.gca().add_artist(circle)
+plt.title("蒙特卡洛方法估算π")
+plt.show()
+```
+
+1. 首先，导入`random`和`matplotlib.pyplot`库。`random`库用于生成随机数，`matplotlib.pyplot`库用于绘制图形。
+2. 定义变量`num_points`，表示要生成的随机点的数量，这里设置为10000。
+3. 初始化变量`points_inside_circle`和`points_total`，分别用于记录落在圆内的点和总点数。初始化变量`x_list`和`y_list`，用于记录每个点的x和y坐标。初始化变量`colors`，用于记录每个点的颜色。
+4. 使用一个循环生成10000个随机点，每个点的x和y坐标都在-1到1之间。如果点的x和y坐标的平方和小于等于1，说明点在圆内，将`points_inside_circle`加1，并将颜色设置为绿色；否则，将颜色设置为蓝色。将点的x和y坐标分别添加到`x_list`和`y_list`中，并将点的颜色添加到`colors`中。
+5. 计算估计的圆的面积，公式为`pi = 4 * points_inside_circle / points_total`。
+6. 使用`matplotlib.pyplot`库绘制图形。首先，设置图形的大小为5x5。然后，设置x轴和y轴的范围为-1到1。接着，使用`scatter`函数绘制散点图，其中`x_list`和`y_list`是点的x和y坐标，`s=8`表示点的大小为8，`c=colors`表示点的颜色，`marker='o'`表示点的形状为圆形。然后，使用`Circle`函数创建一个半径为1的圆，颜色为红色，不填充。最后，使用`add_artist`函数将圆添加到图形中。
+7. 使用`show`函数显示图形