Nurikabe Rules
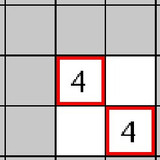
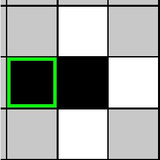
Nurikabe is a puzzle with unfilled squares shown in gray. Your task is to color all the cells white or black according to the rules of the game
Clicking on a gray tile first makes it white
Clicking on a white tile makes it black
Clicking on a black tile returns it to gray
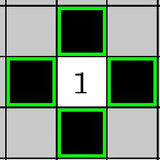
- White Area: an adjacency region of white cells
- Area’s number: The number of the (one!) cell that is part of that area that has a number
- You cannot fill in cells containing numbers black.
- A number cell tells the number of continuous white cells it is connected to INCLUDING itself.
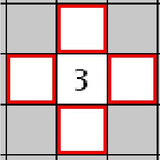
- Each area of white cells contains exactly one number in it, and they are separated by black cells.
- The black cells are linked to form a single continuous wall.
- Black cells cannot be linked to be 2×2 square or larger.
If a tile can be colored either white or black based on the current state of the board, create a split in the tree where the tile is black in one path, and white in the other to show the different cases
If a room can be finished in up to two ways but less than ten ways, create a split in the tree with branches of each possible way white tiles can be added to finish the room.
This rule comes directly from Rule #5. If a black 2x2 square is formed and there is no derivation around forming said square, the board is in a state of contradiction.
This rule comes directly from Rule #4. If a black wall is unable to meet when following a derivation of a board, there is a contradiction and the board is in a state of contradiction.
This rule comes directly from Rule #3. If a white region containing multiple numbers is formed, place a wall between the regions to avoid a contradiction
This rule comes directly from Rule #3. If a derivation leads to a white region that contains no numbers, the board is in a state of contradiction
This rule comes directly from Rule #2. If a derivation that leads to a white region containing too few white tiles is unable to be fixed by expanding the region, the board case is in a state of contradiction
This rule comes directly from Rule #2. If a derivation that leads to a white region containing too many white tiles is unable to be fixed without placing illegal black tiles, the board is in a state of contradiction.
Rule is a combination of Rule #2 and Rule #3. If an unknown cell cannot be reached from any area by any path while making sure that the number of cells in the area don’t exceed the number, then the unknown should be black.
This rule comes directly from Rule #3. If there are two white areas with a different number, and there is an unknown cell that is adjacent to both areas, then the unknown should be made black.
This rule is a derivation of Rule #4. If there is only one unknown adjacent to a black adjacency region, and there are other black cells that don’t belong to that region, then the unknown should be made black.
This rule is a derivation of Rule #3. If an unknown square is not within reach of any number cells to color it black, color the unknown square black.
This rule is a derivation of Rule #4. If a white area needs only one more white cell, and there are two unknown adjacent to that area, and a third unknown adjacent to both of these two unknowns, then the third unknown must be black.
This rule is a derivation from Rule #4. If a unfilled square is surrounded by black tiles, then the unknown square should be filled in black
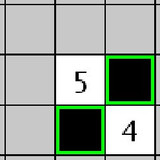
This rule is a derivation from Rule #4. If there is only one unknown adjacent to a white area, and that area’s number is higher than the number of cells currently in that area, then the unknown should be made white.
This rule is a derivation from Rule #5. If three out of four cells of a 2x2 block of cells are black, and the fourth is unknown, then the unknown should be made white.
This rule is a derivation of Rule #2. All the unknown cells that are adjacent to a white area that contains exactly the right number of cells should be made black
This rule is a derivation of Rule #2. If there is only one unknown adjacent to a white area, and that area does not contain any number, then the unknown should be made white
This rule is a derivation of Rule #2. If there is an area with a number, and a second area without a number, and an unknown adjacent to both areas, then if the sum of the number of cells of the two areas plus 1 is larger than the first area’s number, then the unknown should be made black