-
Notifications
You must be signed in to change notification settings - Fork 128
Tutorial Beziers_for_Beginners
Bézier curves are parametric curves defined by polynomial equations. To work with Béziers in OpenSCAD we need to load BOSL2/std.scad, which includes the extension beziers.scad.
Bézier curves vary by the degree of the polynomial that defines the curve.
Quadratic Béziers, i.e. Bezier's of degree 2, are defined by quadratic polynomials. A quadratic Bézier has a starting control point, an ending control point, and, one intermediate control point that most often does not lie on the curve. The curve starts toward the intermediate control point and then turns so that it arrives at the endpoint from the direction of the intermediate control point.

To visualize a Bézier curve we can use the module debug_bezier(). The argument N tells debug_bezier the degree of the Bézier curve.
include<BOSL2/std.scad>
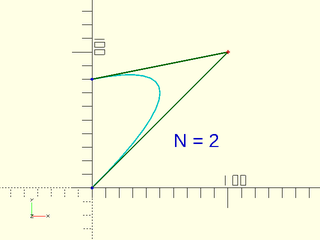
bez = [[0,0], [30,60], [0,100]];
debug_bezier(bez, N = 2);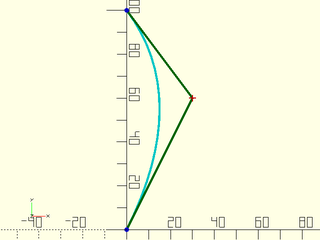
If we move any of the control points, we change the shape of the curve.
include<BOSL2/std.scad>
bez = [[0,0], [100,50], [0,100]];
debug_bezier(bez, N = 2);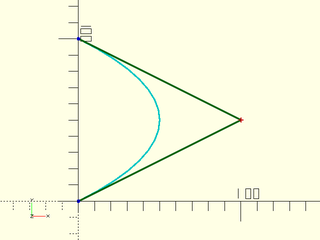
Cubic Bézier curves (degree 3) are defined by cubic polynomials. A cubic Bézier has four control points. The first and last control points are the endpoints of the curve. The curve starts toward the second control point and then turns so that it arrives at the endpoint from the direction of the third control point.

include<BOSL2/std.scad>
bez = [[20,0], [100,40], [50,90], [25,80]];
debug_bezier(bez, N = 3);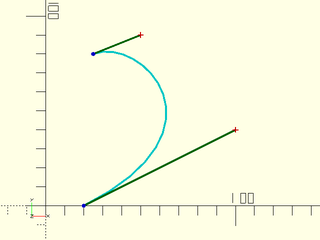
By moving the second and third points on the list we change the shape of the curve.
include<BOSL2/std.scad>
bez = [[20,0], [60,40], [-20,50], [25,80]];
debug_bezier(bez, N = 3);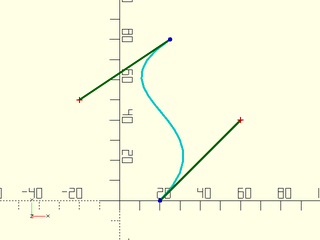
For a live example of cubic Béziers see the Desmos Graphing Calculator.
Higher order Béziers such as quartic (degree 4) and quintic (degree 5) Béziers exist as well. Degree 4 Béziers are used by round_corners() and in the continuous rounding operations of rounded_prism().

Beziers with higher degree, and hence more control points, offer more control over the shape of the bezier curve. You can add more control points to a bezier if you need to refine the shape of the curve.
Bézier curves are not restricted to the XY plane. We can define a 3d Bézier as easily as a 2d Bézier.
include<BOSL2/std.scad>
bez = [[10,0,10], [30,30,-10], [-30,30,40], [-10,0,30]];
debug_bezier(bez, N = 3);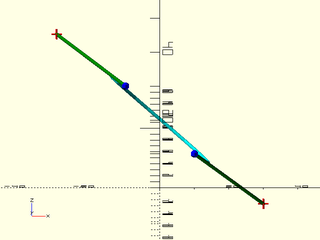
A Bézier path is when we string together a sequence of Béziers with coincident endpoints.
The point counts arise as a natural consequence of what a Bézier path is. If you have k Béziers of order N, then that's k(N+1) points, except we have k-1 overlaps, so instead it's
The list of control points for a Bézier is not an OpenSCAD path. If we treat the list bez[] as a path we would get a very different shape. Here the Bézier is in green and the OpenSCAd path through the control points is in red.
include<BOSL2/std.scad>
bez = [[20,0], [60,40], [-20,50], [25,80]];
debug_bezier(bez, N = 3);
color("red") stroke(bez);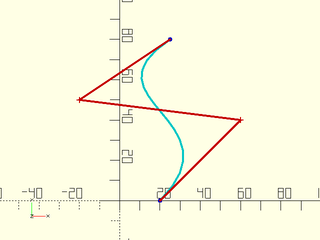
To convert the Bézier curve to an OpenSCAD path, use the bezpath_curve() function.
include<BOSL2/std.scad>
bez = [[20,0], [60,40], [-20,50], [25,80]];
path = bezpath_curve(bez, N = 3);
stroke(path);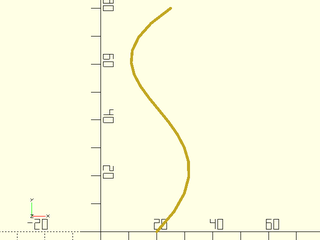
Bézier paths can be made up of more than one Bézier curve. Quadratic Bezier paths have a multiple of 2 points plus 1, and cubic Bézier paths have a multiple of 3 points plus 1
This means that a series of 7 control points can be grouped into three (overlapping) sets of 3 and treated as a sequence of 3 quadratic Béziers. The same 7 points can be grouped into two overlapping sets of 4 and treated as a sequence of two cubic Béziers. The two paths have significantly different shapes.
include<BOSL2/std.scad>
bez = [[0,0], [10,30], [20,0], [30,-30], [40,0], [50,30],[60,0]];
path = bezpath_curve(bez, N = 2); //make a quadratic Bézier path
stroke(path);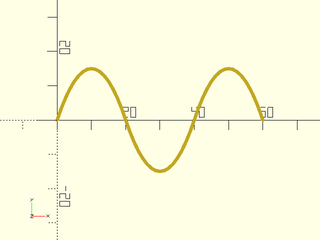
include<BOSL2/std.scad>
bez = [[0,0], [10,30], [20,0], [30,-30], [40,0], [50,30],[60,0]];
path = bezpath_curve(bez, N=3); //make a cubic Bézier path
stroke(path);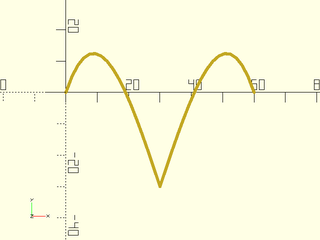
By default bezpath_curve() takes a Bézier path and converts it to an OpenSCAD path by splitting each Bézier curve into 16 straight-line segments. The segments are not necessarily of equal length. The special variable $fn has no effect on the number of steps. You can control this number using the splinesteps argument.
include<BOSL2/std.scad>
bez = [[20,0], [60,40], [-20,50], [25,80]];
path = bezpath_curve(bez, splinesteps = 6);
stroke(path);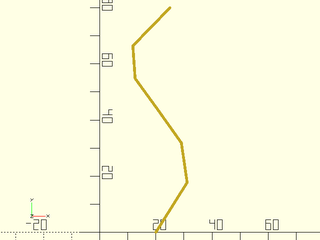
To close the path to the y-axis we can use the bezpath_close_to_axis() function.
include<BOSL2/std.scad>
bez = [[20,0], [60,40], [-20,50], [25,80]];
closed = bezpath_close_to_axis(bez, axis = "Y");
path = bezpath_curve(closed);
stroke(path, width = 2);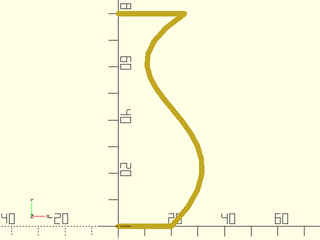
If we use rotate_sweep() to sweep that path around the y-axis we have a solid vase-shaped object. Here we're using both $fn and the splinesteps argument to produce a smoother object.
include<BOSL2/std.scad>
$fn = 72;
bez = [[20,0], [60,40], [-20,50], [25,80]];
closed = bezpath_close_to_axis(bez, axis = "Y");
path = bezpath_curve(closed, splinesteps = 32);
rotate_sweep(path,360);
Instead of closing the path all the way to the y-axis, we can use bezpath_offset() to duplicate the path 5 units to the left, and close the two paths at the top and bottom. Note that bezpath_offset takes an x,y pair as an offset value.
include<BOSL2/std.scad>
$fn = 72;
bez = [[20,0], [60,40], [-20,50], [25,80]];
closed = bezpath_offset([-5,0], bez);
debug_bezier(closed);
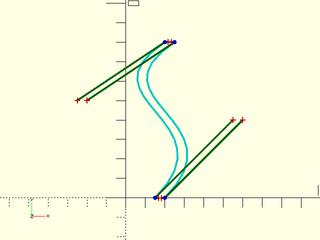
Note that bezpath_offset() does not ensure a uniform wall thickness. For a constant-width wall we need to offset the path along the normals. This we can do using offset(), but we must first convert the Bézier to an OpenSCAD path, then reverse the offset path to create a closed path.
We could also do this using offset_stroke() as a function. The offset_stroke() function automates offsetting the path, reversing it and closing the path all in one step. To use offset_stroke(), we must also include the file rounding.scad.
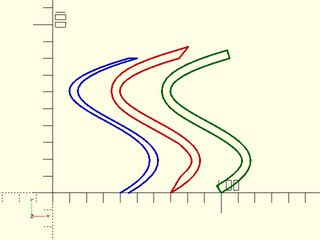
You can see the differences between the three methods here, with bezpath_offset() in blue, offset() in red, and offset_stroke() in green.
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fn = 72;
bez = [[40,0], [110,40], [-60,50], [45,80]];
bez2 = bezpath_offset([5,0], bez);
path= bezpath_curve(bez2, splinesteps = 32);
color("blue") stroke(path);
path2 = bezier_curve(bez, splinesteps = 32);
closed2 = concat(path2,reverse(offset(path2,delta=5)),[bez[0]]);
right(30) color("red") stroke(closed2);
path3 = offset_stroke(bezier_curve(bez, splinesteps = 32), [5,0]);
right(60) color("green") stroke(path3, closed= true);
Sweeping a Bézier path offset using any of the three methods around the y-axis gives us a shape with an open interior. However, as this cross section shows, our new path does not close the bottom of the vase.
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fn = 72;
bez = [[15,0], [60,40], [-25,50], [25,80]];
path = offset_stroke(bezier_curve(bez, splinesteps = 32), [2,0]);
back_half(s = 200) rotate_sweep(path,360);
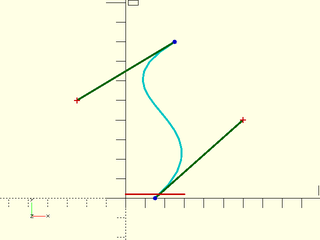
We use a cylinder with a height of 2 for the floor of our vase. At the bottom of the vase the radius of the hole is bez[0].x but we need to find the radius at y = 2. The function bezier_line_intersection() returns a list of u-values where a given line intersects our Bézier curve.
The u-value is a number between 0 and 1 that designates how far along the curve the intersections occur. In our case the line crosses the Bézier only at one point so we get the single-element list [0.0168783].
The function bezier_points() converts that list of u-values to a list of x,y coordinates. Drawing a line at y = 2 gives us the single-element list 17.1687, 2.
include<BOSL2/std.scad>
bez = [[15,0], [60,40], [-25,50], [25,80]];
debug_bezier(bez, N = 3);
line = [[0,2], [30,2]];
color("red") stroke(line);
u = bezier_line_intersection(bez,line);
echo(bezier_points(bez,u)); // [[17.1687, 2]]
That means a cyl() with a height of 2, a bottom radius of bez[0].x and a top radius of 17.1687 fits our vase.
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
$fn = 72;
bez = [[15,0], [60,40], [-25,50], [25,80]];
path = offset_stroke(bezier_curve(bez, splinesteps = 32), [0,2]);
back_half(s = 200) rotate_sweep(path,360);
line = [[0,2], [30,2]];
u = bezier_line_intersection(bez,line).x;
r2 = bezier_points(bez,u).x;
color("red") cyl(h = 2, r1 = bez[0].x, r2 = r2, anchor = BOT);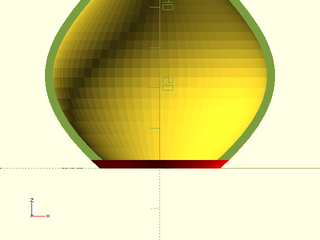
Keep in mind the fact that $fn controls the smoothness of the rotate_sweep() operation while the smoothness of the Bézier is controlled by the splinesteps argument.
include<BOSL2/std.scad>
$fn = 72;
bez = [[15,0], [40,40], [-20,50], [20,80]];
closed = bezpath_offset([2,0], bez);
path = bezpath_curve(closed, splinesteps = 64);
rotate_sweep(path,360, $fn = 72);
right(60) rotate_sweep(path,360, $fn = 6);
right(120) rotate_sweep(path,360, $fn = 4);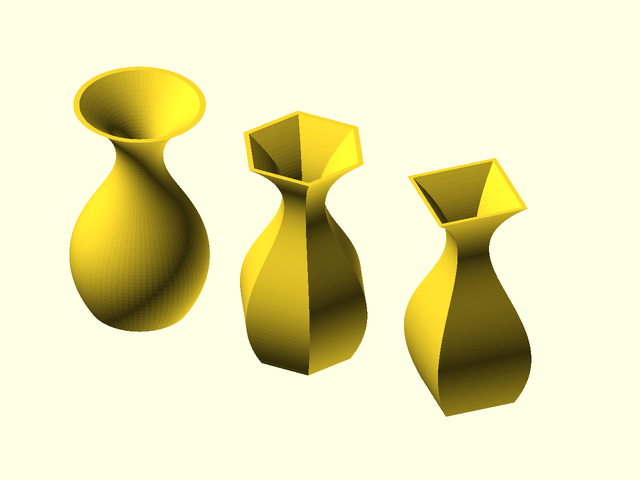
Paths constructed as a series of cubic Bézier curves are familiar to users of Inkscape, Adobe Illustrator, and Affinity Designer. The Bézier Game illustrates how these drawing programs work.
BOSL2 includes four functions for constructing Cubic Bézier paths:
bez_begin() and bez_end() define the endpoints of a simple cubic Bézier curve.
Because each constructor function produces a list of points , we use the flatten() function to consolidate them into a single list.
There are three different ways to specify the location of the endpoints and control points.
First, you can specify the endpoints by vectors and the control points by angle, measured from X+ in the XY plane, and distance:
include<BOSL2/std.scad>
bez = flatten([
bez_begin([0,0], 45, 42.43),
bez_end([100,0], 90, 30),
]);
debug_bezier(bez,N=3);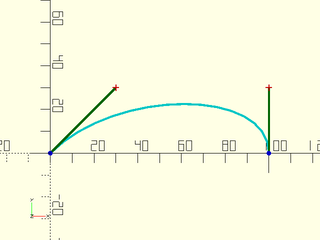
Second, can specify the XY location of the endpoint and that end's control point as a vector from the control point:
include<BOSL2/std.scad>
bez = flatten([
bez_begin([0,0], [30,30]),
bez_end([100,0], [0,30]),
]);
debug_bezier(bez,N=3);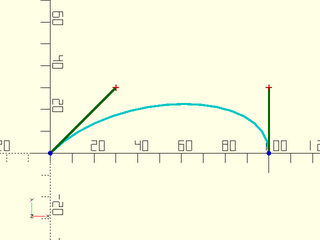
Third, you can specify the endpoints by vectors, and the control points by a direction vector and a distance:
include<BOSL2/std.scad>
bez = flatten([
bez_begin([0,0], BACK+RIGHT, 42.43),
bez_end([100,0], [0,1], 30),
]);
debug_bezier(bez,N=3);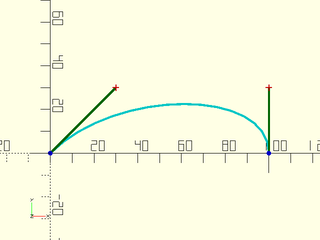
BOSL2 includes the bez_joint() constructor for adding corners to a Bézier path. A corner point has three control points. These are the point on the path where we want the corner, and the approaching and departing control points. We can specify these control points in any of the three ways shown above.
Here's an example using angle and distance to specify a corner. Note that the angles are specified first, and then the distances:
include<BOSL2/std.scad>
bez = flatten([
bez_begin([0,0], 45, 42.43),
bez_joint([40,20], 90,0, 30,30),
bez_end([100,0], 90, 30),
]);
debug_bezier(bez,N=3);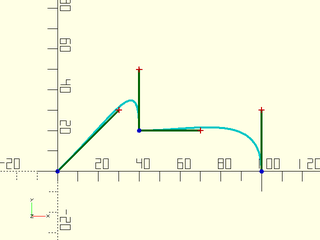
The fourth cubic Bézier path constructor is bez_tang(). This constructor makes smooth joint. It also has three control points, one on the path and the approaching and departing control points. Because all three points lie on a single line, we need to specify only the angle of the departing control point. As in this example you can specify different distances for the approaching and departing controls points. If you specify only a single distance, it is used for both.
We can add a smooth joint to the last example:
include<BOSL2/std.scad>
bez = flatten([
bez_begin([0,0], 45, 42.43),
bez_joint([40,20], 90,0, 30,30),
bez_tang([80,50], 0, 20,40),
bez_end([100,0], 90, 30),
]);
debug_bezier(bez,N=3);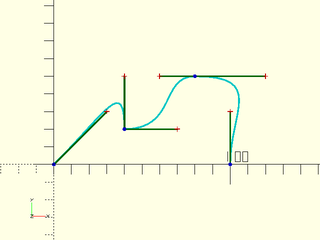
It is not necessary to use the same notation to describe the entire Bézier path. We can mix the Angle, Vector and Vector with Distance notations within a single path:
include<BOSL2/std.scad>
bez = flatten([
bez_begin([0,0], [30,30]),
bez_joint([40,20], BACK,RIGHT, 30,30),
bez_tang([80,50], 0, 20,40),
bez_end([100,0], BACK, 30),
]);
debug_bezier(bez,N=3);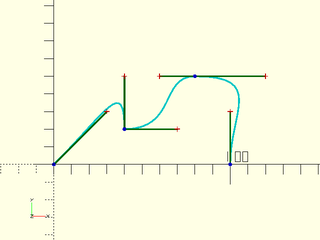
When using the cubic Bézier constructors our Bézier path must always begin with the bez_begin() and bez_end() constructors.
This might make some of the examples in The Bézier Game appear puzzling. Take for example the circle. We can duplicate those results by replacing their starting tangential control point with our beginning and end points.
The correct distance to place the approaching and departing control points to closely approximate a circle is
where r is the radius of the circle and n is the number of bez_tang() segments required to make a full circle. Remember that our bez_begin() and bez_end() segments taken together simulate a bez_tang() segment. For our case, where we're closing the circle in 4 segments, the formula evaluates to r * 0.552284.
include<BOSL2/std.scad>
r = 50; // radius of the circle
n = 4; //bezier segments to complete circle
d = r * (4/3) * tan(180/(2*n)); //control point distance
bez = flatten([
bez_begin([-r,0], 90, d),
bez_tang ([0,r], 0, d),
bez_tang ([r,0], -90, d),
bez_tang ([0,-r], 180, d),
bez_end ([-r,0], -90, d)
]);
debug_bezier(bez, N=3);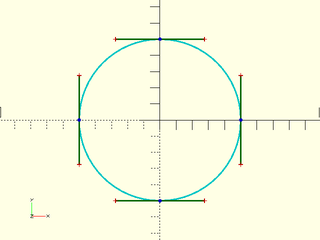
Similarly, for the heart-shaped path we replace a corner point with the start and end points:
include<BOSL2/std.scad>
bez = flatten([
bez_begin([0,25], 40, 40),
bez_joint([0,-25], 30, 150, 60, 60),
bez_end ([0,25], 140, 40)
]);
debug_bezier(bez, N=3);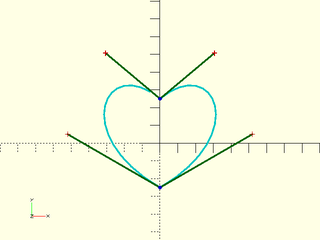
The first shape in The Bézier Game past the stages with hints is the outline of the automobile. Here's how we can duplicate that with our cubic Bézier constructors:
include<BOSL2/std.scad>
bez = flatten([
bez_begin([0,0], BACK, 15),
bez_joint([0,9], FWD, RIGHT, 10,10),
bez_joint([5,9], LEFT, 70, 9,20),
bez_tang([80,65], 3, 35, 20),
bez_joint([130,60], 160, -60, 10, 30),
bez_joint([140,42], 120, 0, 20,55),
bez_joint([208,9], BACK, RIGHT, 10,6),
bez_joint([214,9], LEFT, FWD, 10,10),
bez_joint([214,0], BACK, LEFT, 10,10),
bez_joint([189,0], RIGHT, -95, 10,10),
bez_tang([170,-17], LEFT, 10),
bez_joint([152,0], -85, LEFT, 10,10),
bez_joint([52,0], RIGHT, -95, 10,10),
bez_tang([33,-17], LEFT, 10),
bez_joint([16,0], -85,LEFT, 10,10),
bez_end ([0,0], RIGHT,10)
]);
debug_bezier(bez, N = 3);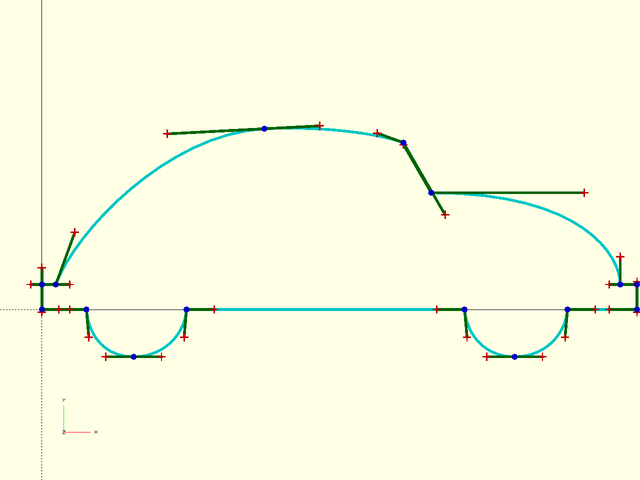
We can make a heart shaped dish using a 2D Bézier path to define the shape. When we convert the Bézier curve to a Bézier path with bezpath_curve() we can smooth the resulting path by increasing splinesteps to 64.
include<BOSL2/std.scad>
include<BOSL2/rounding.scad>
bez = flatten([
bez_begin([0,50], 40, 100),
bez_joint([0,-50], 30, 150, 120, 120),
bez_end ([0,50], 140, 100)
]);
path = bezpath_curve(bez, splinesteps = 64);
linear_sweep(h = 2, path);
region = offset_stroke(path, -3, closed = true);
linear_sweep(h = 20, region);
BOSL2 includes a set of constructor functions for creating cubic Bézier paths. They can create 2d or 3d Béziers. There are constructors for beginning and end points as well as connectors for corner and tangential connections between Bézier curves. Each function gives you the choice of specifying the curve using Angle Notation, Vector Notation, or by Direction Vector and Distance.
The path by angle constructors can be used to create 3D Bézier paths by specifying a 3D point on the curve and listing the angle (from the X axis) and distance to the departing and/or departing control point, then adding a p argument that is the angle away from the Z axis for that control point.
include<BOSL2/std.scad>
bez = flatten([
bez_begin ([-50,0,0], 90, 25, p=90),
bez_joint ([0,50,50], 180,0 , 50,50, p1=45, p2=45),
bez_tang ([50,0,0], -90, 25, p=90),
bez_joint ([0,-50,50], 0,180 , 25,25, p1=135,p2=135),
bez_end ([-50,0,0], -90, 25, p=90)
]);
debug_bezier(bez, N=3);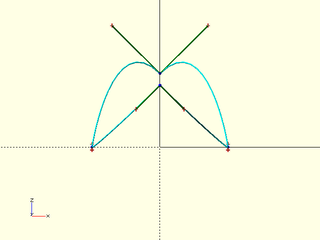
The cubic Bézier path constructors can also be used to create 3D Bézier paths by specifying the control points using vectors. The first vector is the location of the control point that lies on the Bézier path, followed by vectors pointing from that control point to the approaching and/or departing control points.
include<BOSL2/std.scad>
bez = flatten([
bez_begin([-50,0,0], [0,25,0]),
bez_joint([0,50,50], [-35,0,35], [35,0,35]),
bez_tang ([50,0,0], [0,-25,0]),
bez_joint([0,-50,50], [18,0,-18], [-18,0,-18]),
bez_end ([-50,0,0], [0,-25,0])
]);
debug_bezier(bez, N=3);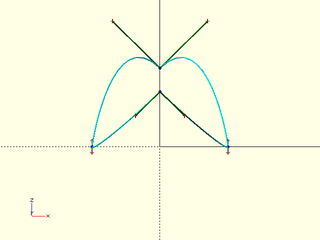
The third method for specifying 3D cubic Bézier Paths is by Direction Vector and distance. For bez_tang() and bez_joint(), if r1 is given and r2 is not, the function uses the value of r1 for r2.
include<BOSL2/std.scad>
bez = flatten([
bez_begin([-50,0,0], BACK, 25),
bez_joint([0,50,50], LEFT+UP, RIGHT+UP, 50,50),
bez_tang ([50,0,0], FWD, 25),
bez_joint([0,-50,50], RIGHT+DOWN, LEFT+DOWN, 25,25),
bez_end ([-50,0,0], FWD, 25)
]);
debug_bezier(bez, N=3);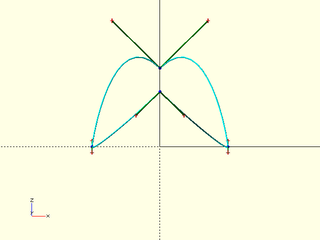
We can use a 2D Bézier path to define the shape of our bud vase as we did in the examples above. Instead of using a rotate_sweep() to make a vase with a circular cross section we use a 3D Bèzier path that both defines the cross section and makes the top more interesting. This design uses the skin() module to create the final geometry.
include<BOSL2/std.scad>
//Side Bézier Path
side_bez = [[20,0], [40,40], [-10,70], [20,100]];
side = bezpath_curve(side_bez, splinesteps = 32);
h = last(side).y;
steps = len(side)-1;
step = h/steps;
wall = 2;
//Layer Bézier Path
size = side_bez[0].x; // size of the base
d = size * 0.8; // intermediate control point distance
theta = 65; // adjusts layer "wavyness".
bz = 5 * cos(theta); // offset to raise layer curve minima above z = 0;
layer_bez = flatten([
bez_begin ([-size,0,bz], 90, d, p=theta),
bez_tang ([0, size,bz], 0, d, p=theta),
bez_tang ([size, 0,bz], -90, d, p=theta),
bez_tang ([0,-size,bz], 180, d, p=theta),
bez_end ([-size,0,bz], -90, d, p=180 - theta)
]);
layer = bezpath_curve(layer_bez);
function layer_xy_scale(z) =
let (sample_z = side_bez[0].y + z * step) // the sampling height
let (u = bezier_line_intersection(side_bez, [[0, sample_z],[1, sample_z]]))
flatten(bezier_points(side_bez,u)).x / side_bez[0].x;
outside =[for(i=[0:steps]) scale([layer_xy_scale(i),layer_xy_scale(i),1],up(i*step, layer))];
inside = [for (curve = outside) hstack(offset(path2d(curve), delta = -2, same_length = true), column(curve,2))];
base = path3d(path2d(outside[0])); //flatten the base but keep as a 3d path
floor = up(wall, path3d(offset(path2d(outside[0]), -wall)));
skin([ base, each outside, each reverse(inside), floor ], slices=0, refine=1, method="fast_distance");

Table of Contents
Function Index
Topics Index
Cheat Sheet
Tutorials
Basic Modeling:
- constants.scad STD
- transforms.scad STD
- attachments.scad STD
- shapes2d.scad STD
- shapes3d.scad STD
- drawing.scad STD
- masks2d.scad STD
- masks3d.scad STD
- distributors.scad STD
- color.scad STD
- partitions.scad STD
- miscellaneous.scad STD
Advanced Modeling:
- paths.scad STD
- regions.scad STD
- skin.scad STD
- vnf.scad STD
- beziers.scad STD
- nurbs.scad
- rounding.scad
- turtle3d.scad
- isosurface.scad
Math:
- math.scad STD
- linalg.scad STD
- vectors.scad STD
- coords.scad STD
- geometry.scad STD
- trigonometry.scad STD
Data Management:
- version.scad STD
- comparisons.scad STD
- lists.scad STD
- utility.scad STD
- strings.scad STD
- structs.scad STD
- fnliterals.scad
Threaded Parts:
Parts:
- ball_bearings.scad
- cubetruss.scad
- gears.scad
- hinges.scad
- joiners.scad
- linear_bearings.scad
- modular_hose.scad
- nema_steppers.scad
- polyhedra.scad
- sliders.scad
- tripod_mounts.scad
- walls.scad
- wiring.scad
STD = Included in std.scad