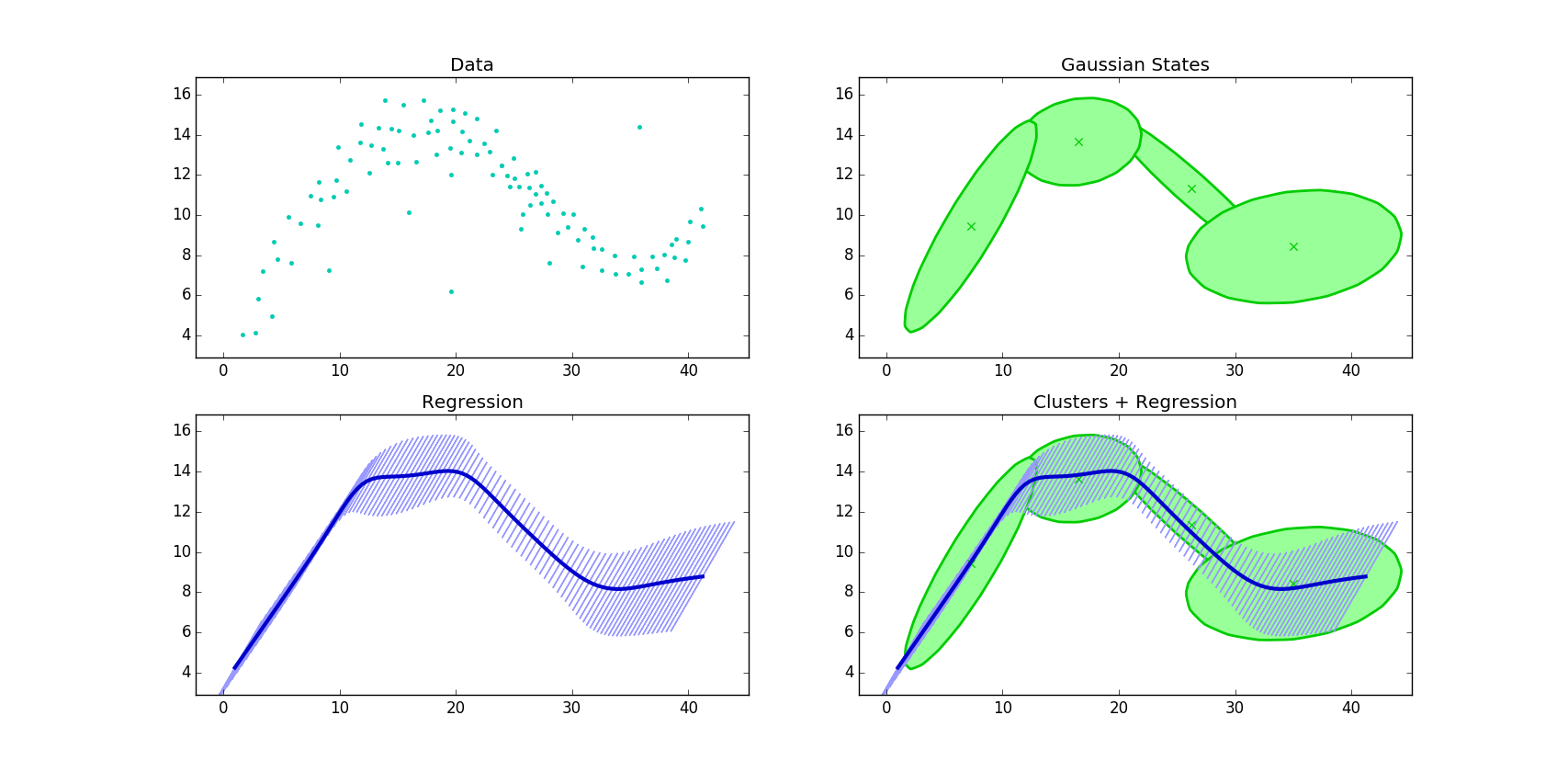
Python implementation of Gaussian Mixture Regression(GMR) and Gaussian Mixture Model(GMM) algorithms with examples and data files. GMM is a soft clustering algorithm which considers data as finite gaussian distributions with unknown parameters. Current approach uses Expectation-Maximization(EM) algorithm to find gaussian states parameters. EM is an iterative algorithm which converges to true gaussian parameters and stopped by log-likelihood threshold or iteration number limit. To initialize gaussian parameters k-means clustering algorithm is used. After GMM is fitted, the model is used to fit GMR to retrieve output features by time input.
My associated papers with this project:
Saduanov, B., Alizadeh, T., An, J., & Abibullaev, B. (2018, January). Trained by demonstration humanoid robot controlled via a BCI system for telepresence. In Brain-Computer Interface (BCI), 2018 6th International Conference on (pp. 1-4). IEEE.
Saduanov, B., Tokmurzina, D., Alizadeh, T., & Abibullaev, B. (2018, March). Brain-Computer Interface Humanoid Pre-trained for Interaction with People. In Companion of the 2018 ACM/IEEE International Conference on Human-Robot Interaction (pp. 229-230). ACM.
All math and concepts are referred from the book and MATLAB implementation both by professor Sylvain Calinon (http://calinon.ch):
Calinon, S. (2009) Robot Programming by Demonstration: A Probabilistic Approach EPFL Press ISBN 978-2-940222-31-5, CRC Press ISBN 978-1-4398-0867-2. http://calinon.ch/paper6001.htm
MATLAB implementation: https://www.mathworks.com/matlabcentral/fileexchange/19630-gaussian-mixture-model--gmm--gaussian-mixture-regression--gmr-
Additional sources:
Tsishchanka, K. Elementary Statistics: Chapter 9 http://www.tkiryl.com/Elementary%20Statistics/Chapter_9.pdf
Mathworks documentation Clustering Using Gaussian Mixture Models http://www.mathworks.com/help/stats/clustering-using-gaussian-mixture-models.html
Princeton University Library Data and Statistical Services: Introduction to Regression http://dss.princeton.edu/online_help/analysis/regression_intro.htm
Clone or download the project
Install following packages: numpy <1.11.3>, matplotlib <1.5.3>,
Other versions of the packages were not tested, but higher versions are welcome. Report me to [email protected] if you have any problems.
To use GMM_GMR algorithms copy all python files to your folder. In your main script
file import GMM_GMR class by writing from GMM_GMR import GMM_GMR. To create instance
of GMM_GMR just call its constructor with one parameters which defines number of clusters, for example:
gmm = GMM_GMR(4)
To fit data to GMR use method
fit(numpy.array: data)
Data should be of numpy.array(type = float) type, and has dimension of NxM, where N is a number of features and M is a number of recordings or data points. Data matrix should have first row as time series variable. Regression considers first row as independent input variable and other rows as dependent (on first row) output variables. To predict outputs, create one dimensional input array A and call
predict(np.array: input)
function passing A as an argument to this method. To plot clusters or predicted regression data use plot function which has 7 parameters which are predefined already and they are:
xAxis = 0, yAxis = 1, plotType = "Clusters", ax = plt, dataColor = [0, 0.8, 0.7], clusterColor = [0, 0.8, 0], regressionColor = [0,0,0.8]
where 'xAxis' and 'yAxis' parameters are integers representing row index of Data matrix to be plotted on x and y axes respectively, 'plotType' is a string to choose from several possible plot types which are: "Data", "Clusters" and "Regression", 'ax' is a matplotlib plot object representing pyplot frame on which current plot should be drawn, 'dataColor', 'clusterColor' and 'regressionColor' parameters are lists representing [r, g, b] colors of data, cluster and regression plot colors respectively.
There are several possibilities to improve this algorithm implementation. One of them is to make regression more flexible and work not only on one independent time series variable. Actually, this GMR implementation is able to have several independent inputs and retrieve remaining dependent outputs, but it should be tested on such data sets. At such testing stage there can be several bugs in GMR function, but only at the initialization stage with input and output Mu and Sigma declarations. Mathematical side has no any bugs, so if you try to contribute, you will have no mathematical bugs which are usually painfull to fix. If such tests will be successful and all bugs will be fixed, then 2 more parameters should be added to 'predict(np.array: input)' method which will be input and output features indexes passed as numpy arrays or python lists.