You are given a positive integer k. You are also given:
- a 2D integer array
rowConditionsof sizenwhererowConditions[i] = [abovei, belowi], and - a 2D integer array
colConditionsof sizemwherecolConditions[i] = [lefti, righti].
The two arrays contain integers from 1 to k.
You have to build a k x k matrix that contains each of the numbers from 1 to k exactly once. The remaining cells should have the value 0.
The matrix should also satisfy the following conditions:
- The number
aboveishould appear in a row that is strictly above the row at which the numberbelowiappears for allifrom0ton - 1. - The number
leftishould appear in a column that is strictly left of the column at which the numberrightiappears for allifrom0tom - 1.
Return any matrix that satisfies the conditions. If no answer exists, return an empty matrix.
Example 1:
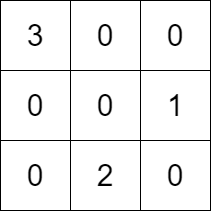
Input: k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]] Output: [[3,0,0],[0,0,1],[0,2,0]] Explanation: The diagram above shows a valid example of a matrix that satisfies all the conditions. The row conditions are the following: - Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix. - Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix. The column conditions are the following: - Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix. - Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix. Note that there may be multiple correct answers.
Example 2:
Input: k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]] Output: [] Explanation: From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied. No matrix can satisfy all the conditions, so we return the empty matrix.
Constraints:
2 <= k <= 4001 <= rowConditions.length, colConditions.length <= 104rowConditions[i].length == colConditions[i].length == 21 <= abovei, belowi, lefti, righti <= kabovei != belowilefti != righti
Topological Sort.
class Solution:
def buildMatrix(
self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]
) -> List[List[int]]:
def f(cond):
g = defaultdict(list)
indeg = [0] * (k + 1)
for a, b in cond:
g[a].append(b)
indeg[b] += 1
q = deque([i for i, v in enumerate(indeg[1:], 1) if v == 0])
res = []
while q:
for _ in range(len(q)):
i = q.popleft()
res.append(i)
for j in g[i]:
indeg[j] -= 1
if indeg[j] == 0:
q.append(j)
return None if len(res) != k else res
row = f(rowConditions)
col = f(colConditions)
if row is None or col is None:
return []
ans = [[0] * k for _ in range(k)]
m = [0] * (k + 1)
for i, v in enumerate(col):
m[v] = i
for i, v in enumerate(row):
ans[i][m[v]] = v
return ansclass Solution {
private int k;
public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {
this.k = k;
List<Integer> row = f(rowConditions);
List<Integer> col = f(colConditions);
if (row == null || col == null) {
return new int[0][0];
}
int[][] ans = new int[k][k];
int[] m = new int[k + 1];
for (int i = 0; i < k; ++i) {
m[col.get(i)] = i;
}
for (int i = 0; i < k; ++i) {
ans[i][m[row.get(i)]] = row.get(i);
}
return ans;
}
private List<Integer> f(int[][] cond) {
List<Integer>[] g = new List[k + 1];
Arrays.setAll(g, key -> new ArrayList<>());
int[] indeg = new int[k + 1];
for (var e : cond) {
int a = e[0], b = e[1];
g[a].add(b);
++indeg[b];
}
Deque<Integer> q = new ArrayDeque<>();
for (int i = 1; i < indeg.length; ++i) {
if (indeg[i] == 0) {
q.offer(i);
}
}
List<Integer> res = new ArrayList<>();
while (!q.isEmpty()) {
for (int n = q.size(); n > 0; --n) {
int i = q.pollFirst();
res.add(i);
for (int j : g[i]) {
if (--indeg[j] == 0) {
q.offer(j);
}
}
}
}
return res.size() == k ? res : null;
}
}class Solution {
public:
int k;
vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {
this->k = k;
auto row = f(rowConditions);
auto col = f(colConditions);
if (row.empty() || col.empty()) return {};
vector<vector<int>> ans(k, vector<int>(k));
vector<int> m(k + 1);
for (int i = 0; i < k; ++i) {
m[col[i]] = i;
}
for (int i = 0; i < k; ++i) {
ans[i][m[row[i]]] = row[i];
}
return ans;
}
vector<int> f(vector<vector<int>>& cond) {
vector<vector<int>> g(k + 1);
vector<int> indeg(k + 1);
for (auto& e : cond) {
int a = e[0], b = e[1];
g[a].push_back(b);
++indeg[b];
}
queue<int> q;
for (int i = 1; i < k + 1; ++i) {
if (!indeg[i]) {
q.push(i);
}
}
vector<int> res;
while (!q.empty()) {
for (int n = q.size(); n; --n) {
int i = q.front();
res.push_back(i);
q.pop();
for (int j : g[i]) {
if (--indeg[j] == 0) {
q.push(j);
}
}
}
}
return res.size() == k ? res : vector<int>();
}
};func buildMatrix(k int, rowConditions [][]int, colConditions [][]int) [][]int {
f := func(cond [][]int) []int {
g := make([][]int, k+1)
indeg := make([]int, k+1)
for _, e := range cond {
a, b := e[0], e[1]
g[a] = append(g[a], b)
indeg[b]++
}
q := []int{}
for i, v := range indeg[1:] {
if v == 0 {
q = append(q, i+1)
}
}
res := []int{}
for len(q) > 0 {
for n := len(q); n > 0; n-- {
i := q[0]
q = q[1:]
res = append(res, i)
for _, j := range g[i] {
indeg[j]--
if indeg[j] == 0 {
q = append(q, j)
}
}
}
}
if len(res) == k {
return res
}
return []int{}
}
row := f(rowConditions)
col := f(colConditions)
if len(row) == 0 || len(col) == 0 {
return [][]int{}
}
m := make([]int, k+1)
for i, v := range col {
m[v] = i
}
ans := make([][]int, k)
for i := range ans {
ans[i] = make([]int, k)
}
for i, v := range row {
ans[i][m[v]] = v
}
return ans
}function buildMatrix(
k: number,
rowConditions: number[][],
colConditions: number[][],
): number[][] {
function f(cond) {
const g = Array.from({ length: k + 1 }, () => []);
const indeg = new Array(k + 1).fill(0);
for (const [a, b] of cond) {
g[a].push(b);
++indeg[b];
}
const q = [];
for (let i = 1; i < indeg.length; ++i) {
if (indeg[i] == 0) {
q.push(i);
}
}
const res = [];
while (q.length) {
for (let n = q.length; n; --n) {
const i = q.shift();
res.push(i);
for (const j of g[i]) {
if (--indeg[j] == 0) {
q.push(j);
}
}
}
}
return res.length == k ? res : [];
}
const row = f(rowConditions);
const col = f(colConditions);
if (!row.length || !col.length) return [];
const ans = Array.from({ length: k }, () => new Array(k).fill(0));
const m = new Array(k + 1).fill(0);
for (let i = 0; i < k; ++i) {
m[col[i]] = i;
}
for (let i = 0; i < k; ++i) {
ans[i][m[row[i]]] = row[i];
}
return ans;
}