给你一个二维整数数组 circles ,其中 circles[i] = [xi, yi, ri] 表示网格上圆心为 (xi, yi) 且半径为 ri 的第 i 个圆,返回出现在 至少一个 圆内的 格点数目 。
注意:
- 格点 是指整数坐标对应的点。
- 圆周上的点 也被视为出现在圆内的点。
示例 1:
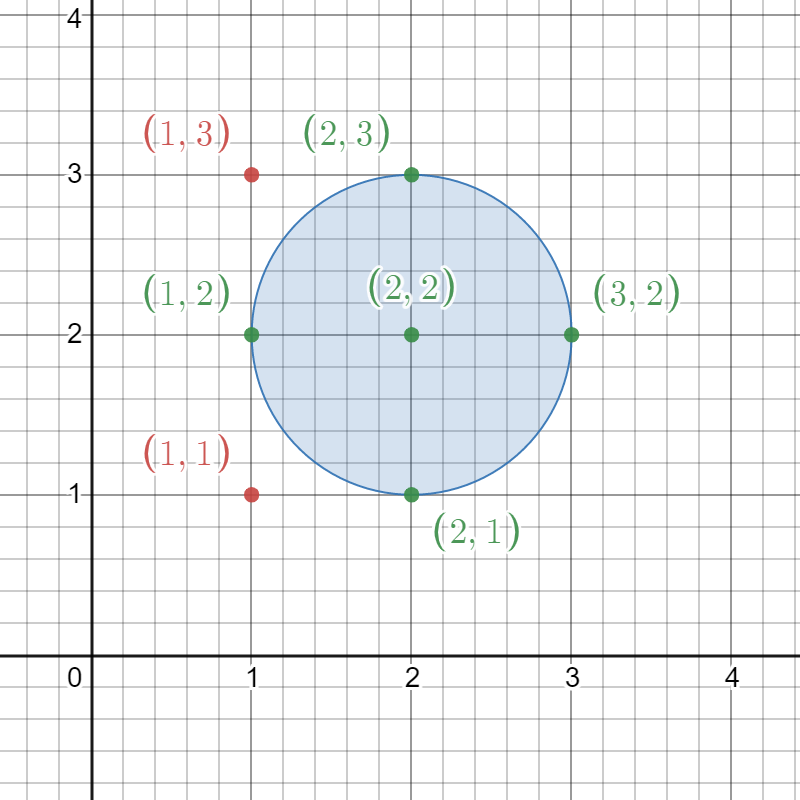
输入:circles = [[2,2,1]] 输出:5 解释: 给定的圆如上图所示。 出现在圆内的格点为 (1, 2)、(2, 1)、(2, 2)、(2, 3) 和 (3, 2),在图中用绿色标识。 像 (1, 1) 和 (1, 3) 这样用红色标识的点,并未出现在圆内。 因此,出现在至少一个圆内的格点数目是 5 。
示例 2:
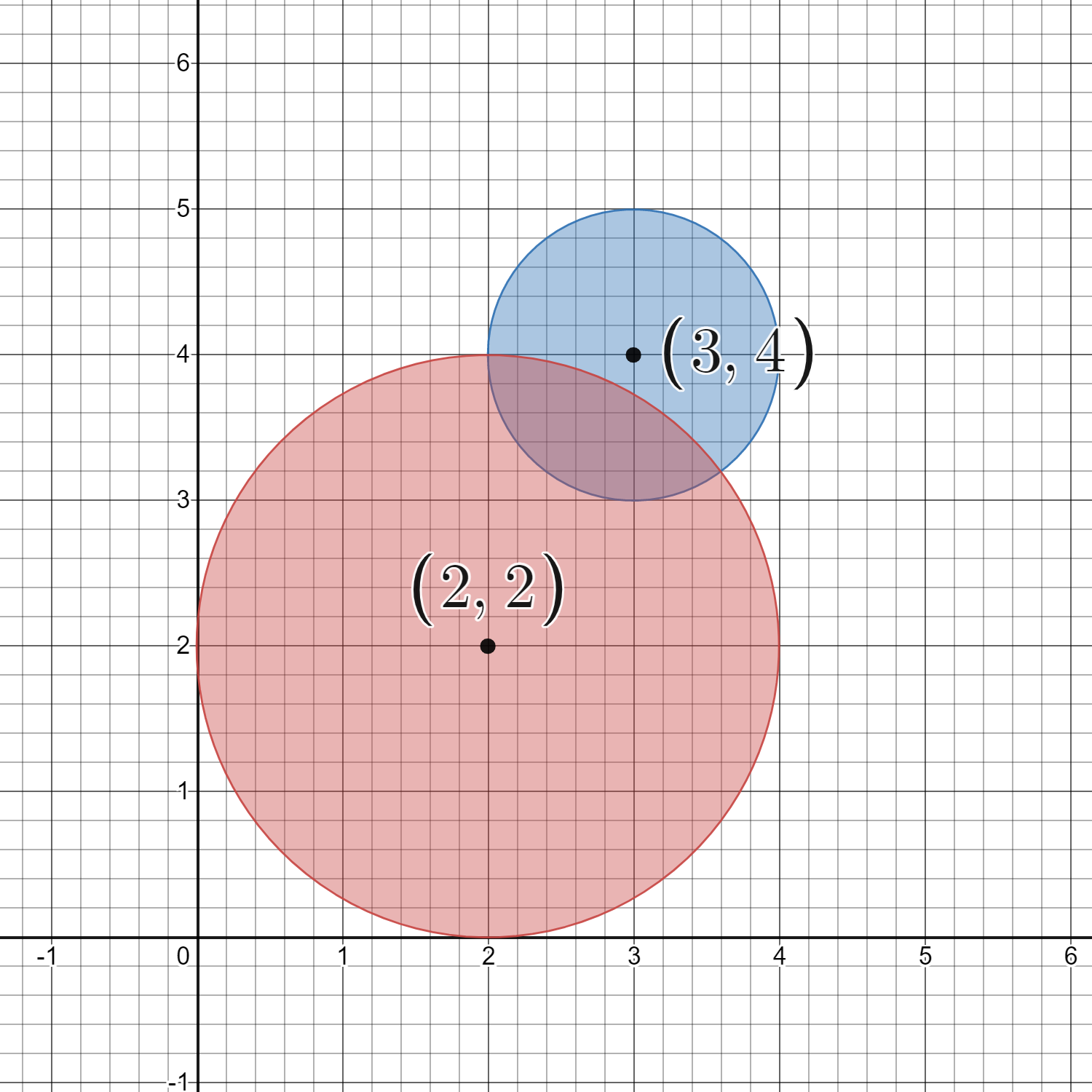
输入:circles = [[2,2,2],[3,4,1]] 输出:16 解释: 给定的圆如上图所示。 共有 16 个格点出现在至少一个圆内。 其中部分点的坐标是 (0, 2)、(2, 0)、(2, 4)、(3, 2) 和 (4, 4) 。
提示:
1 <= circles.length <= 200circles[i].length == 31 <= xi, yi <= 1001 <= ri <= min(xi, yi)
方法一:枚举
枚举所有的格点,判断其是否在圆内,如果在圆内,则答案加一。
枚举的时候,可以将所有圆的最大横纵坐标求出来,作为枚举的上界。
时间复杂度
class Solution:
def countLatticePoints(self, circles: List[List[int]]) -> int:
ans = 0
mx = max(x + r for x, _, r in circles)
my = max(y + r for _, y, r in circles)
for i in range(mx + 1):
for j in range(my + 1):
for x, y, r in circles:
dx, dy = i - x, j - y
if dx * dx + dy * dy <= r * r:
ans += 1
break
return ansclass Solution {
public int countLatticePoints(int[][] circles) {
int mx = 0, my = 0;
for (var c : circles) {
mx = Math.max(mx, c[0] + c[2]);
my = Math.max(my, c[1] + c[2]);
}
int ans = 0;
for (int i = 0; i <= mx; ++i) {
for (int j = 0; j <= my; ++j) {
for (var c : circles) {
int dx = i - c[0], dy = j - c[1];
if (dx * dx + dy * dy <= c[2] * c[2]) {
++ans;
break;
}
}
}
}
return ans;
}
}class Solution {
public:
int countLatticePoints(vector<vector<int>>& circles) {
int mx = 0, my = 0;
for (auto& c : circles) {
mx = max(mx, c[0] + c[2]);
my = max(my, c[1] + c[2]);
}
int ans = 0;
for (int i = 0; i <= mx; ++i) {
for (int j = 0; j <= my; ++j) {
for (auto& c : circles) {
int dx = i - c[0], dy = j - c[1];
if (dx * dx + dy * dy <= c[2] * c[2]) {
++ans;
break;
}
}
}
}
return ans;
}
};func countLatticePoints(circles [][]int) (ans int) {
mx, my := 0, 0
for _, c := range circles {
mx = max(mx, c[0]+c[2])
my = max(my, c[1]+c[2])
}
for i := 0; i <= mx; i++ {
for j := 0; j <= my; j++ {
for _, c := range circles {
dx, dy := i-c[0], j-c[1]
if dx*dx+dy*dy <= c[2]*c[2] {
ans++
break
}
}
}
}
return
}
func max(a, b int) int {
if a > b {
return a
}
return b
}function countLatticePoints(circles: number[][]): number {
let mx = 0;
let my = 0;
for (const [x, y, r] of circles) {
mx = Math.max(mx, x + r);
my = Math.max(my, y + r);
}
let ans = 0;
for (let i = 0; i <= mx; ++i) {
for (let j = 0; j <= my; ++j) {
for (const [x, y, r] of circles) {
const dx = i - x;
const dy = j - y;
if (dx * dx + dy * dy <= r * r) {
++ans;
break;
}
}
}
}
return ans;
}