You are given an m x n binary matrix grid where each cell is either 0 (empty) or 1 (occupied).
You are then given stamps of size stampHeight x stampWidth. We want to fit the stamps such that they follow the given restrictions and requirements:
- Cover all the empty cells.
- Do not cover any of the occupied cells.
- We can put as many stamps as we want.
- Stamps can overlap with each other.
- Stamps are not allowed to be rotated.
- Stamps must stay completely inside the grid.
Return true if it is possible to fit the stamps while following the given restrictions and requirements. Otherwise, return false.
Example 1:
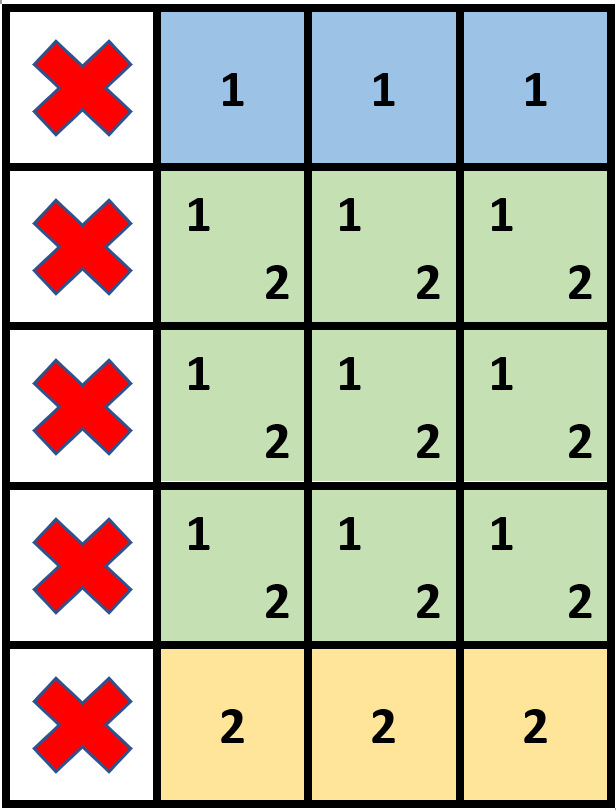
Input: grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3 Output: true Explanation: We have two overlapping stamps (labeled 1 and 2 in the image) that are able to cover all the empty cells.
Example 2:
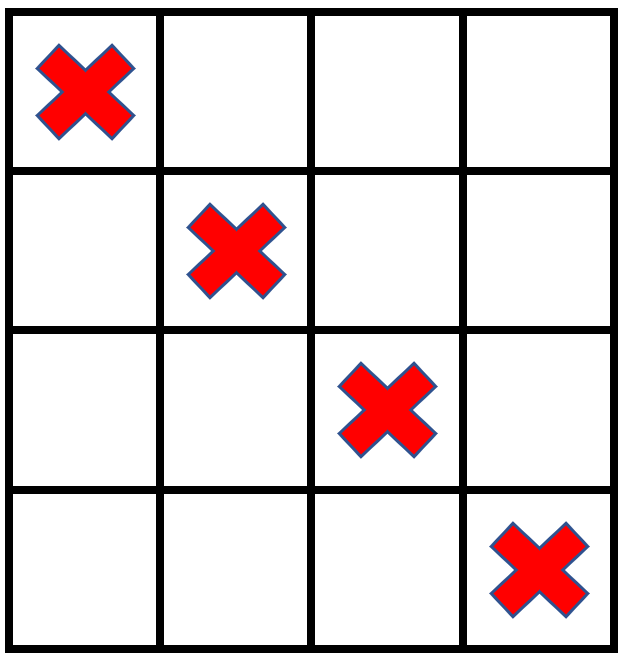
Input: grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2 Output: false Explanation: There is no way to fit the stamps onto all the empty cells without the stamps going outside the grid.
Constraints:
m == grid.lengthn == grid[r].length1 <= m, n <= 1051 <= m * n <= 2 * 105grid[r][c]is either0or1.1 <= stampHeight, stampWidth <= 105
Based on the constraints provided by the question, it's easy to infer that a cell can accommodate a stamp if, after adding the length and width of the stamp, the bottom-right corner does not exceed the boundary, and the sum of all cells in the current sub-area is zero.
Apparently, we can maintain a two-dimensional prefix sum array, and in O(1) time complexity, we can judge whether each cell traversed can accommodate a stamp.
Since the action of affixing a stamp can be generalized to setting the values of all cells in the current sub-area to 1, it's natural to think of maintaining the state after stamp affixing using a two-dimensional difference array.
Finally, just calculate the two-dimensional prefix sum for this difference array again.
If the sum of the current cell is 0, it means there are cases that have not been completely covered, and you can directly return false.
It's worth noting the subscript relationship of the two-dimensional array, which is as follows.
s[i + 1][j + 1] represents the sum of all elements in the upper left part of the i-th row and j-th column, where the subscript i, j starts from 0.
So s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + nums[i][j].
For a sub-matrix with (x1, y1) as the upper left corner and (x2, y2) as the bottom right corner, the sum sub = s[x2 + 1][y2 + 1] - s[x2 + 1][y1] - s[x1][y2 + 1] + s[x1][y1].
class Solution:
def possibleToStamp(
self, grid: List[List[int]], stampHeight: int, stampWidth: int
) -> bool:
m, n = len(grid), len(grid[0])
s = [[0] * (n + 1) for _ in range(m + 1)]
for i, row in enumerate(grid):
for j, v in enumerate(row):
s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + v
d = [[0] * (n + 1) for _ in range(m + 1)]
for i, row in enumerate(grid):
for j, v in enumerate(row):
if v == 0:
x, y = i + stampHeight, j + stampWidth
if x <= m and y <= n and s[x][y] - s[x][j] - s[i][y] + s[i][j] == 0:
d[i][j] += 1
d[i][y] -= 1
d[x][j] -= 1
d[x][y] += 1
cnt = [[0] * (n + 1) for _ in range(m + 1)]
for i, row in enumerate(grid):
for j, v in enumerate(row):
cnt[i + 1][j + 1] = cnt[i + 1][j] + cnt[i][j + 1] - cnt[i][j] + d[i][j]
if v == 0 and cnt[i + 1][j + 1] == 0:
return False
return Trueclass Solution {
public boolean possibleToStamp(int[][] grid, int stampHeight, int stampWidth) {
int m = grid.length, n = grid[0].length;
int[][] s = new int[m + 1][n + 1];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j];
}
}
int[][] d = new int[m + 1][n + 1];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0) {
int x = i + stampHeight, y = j + stampWidth;
if (x <= m && y <= n && s[x][y] - s[x][j] - s[i][y] + s[i][j] == 0) {
d[i][j]++;
d[i][y]--;
d[x][j]--;
d[x][y]++;
}
}
}
}
int[][] cnt = new int[m + 1][n + 1];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
cnt[i + 1][j + 1] = cnt[i + 1][j] + cnt[i][j + 1] - cnt[i][j] + d[i][j];
if (grid[i][j] == 0 && cnt[i + 1][j + 1] == 0) {
return false;
}
}
}
return true;
}
}class Solution {
public:
bool possibleToStamp(vector<vector<int>>& grid, int stampHeight, int stampWidth) {
int m = grid.size(), n = grid[0].size();
vector<vector<int>> s(m + 1, vector<int>(n + 1));
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j];
}
}
vector<vector<int>> d(m + 1, vector<int>(n + 1));
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j]) continue;
int x = i + stampHeight, y = j + stampWidth;
if (x <= m && y <= n && s[x][y] - s[i][y] - s[x][j] + s[i][j] == 0) {
d[i][j]++;
d[x][j]--;
d[i][y]--;
d[x][y]++;
}
}
}
vector<vector<int>> cnt(m + 1, vector<int>(n + 1));
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
cnt[i + 1][j + 1] = cnt[i + 1][j] + cnt[i][j + 1] - cnt[i][j] + d[i][j];
if (grid[i][j] == 0 && cnt[i + 1][j + 1] == 0) return false;
}
}
return true;
}
};impl Solution {
pub fn possible_to_stamp(grid: Vec<Vec<i32>>, stamp_height: i32, stamp_width: i32) -> bool {
let n: usize = grid.len();
let m: usize = grid[0].len();
let mut prefix_vec: Vec<Vec<i32>> = vec![vec![0; m + 1]; n + 1];
// Initialize the prefix vector
for i in 0..n {
for j in 0..m {
prefix_vec[i + 1][j + 1] = prefix_vec[i][j + 1] + prefix_vec[i + 1][j] - prefix_vec[i][j] + grid[i][j];
}
}
let mut diff_vec: Vec<Vec<i32>> = vec![vec![0; m + 1]; n + 1];
// Construct the difference vector based on prefix sum vector
for i in 0..n {
for j in 0..m {
// If the value of the cell is one, just bypass this
if grid[i][j] == 1 {
continue;
}
// Otherwise, try stick the stamp
let x: usize = i + stamp_height as usize;
let y: usize = j + stamp_width as usize;
// Check the bound
if x <= n && y <= m {
// If the region can be sticked (All cells are empty, which means the sum will be zero)
if prefix_vec[x][y] - prefix_vec[x][j] - prefix_vec[i][y] + prefix_vec[i][j] == 0 {
// Update the difference vector
diff_vec[i][j] += 1;
diff_vec[x][y] += 1;
diff_vec[x][j] -= 1;
diff_vec[i][y] -= 1;
}
}
}
}
let mut check_vec: Vec<Vec<i32>> = vec![vec![0; m + 1]; n + 1];
// Check the prefix sum of difference vector, to determine if there is any empty cell left
for i in 0..n {
for j in 0..m {
// If the value of the cell is one, just bypass this
if grid[i][j] == 1 {
continue;
}
// Otherwise, check if the region is empty, by calculating the prefix sum of difference vector
check_vec[i + 1][j + 1] = check_vec[i][j + 1] + check_vec[i + 1][j] - check_vec[i][j] + diff_vec[i][j];
if check_vec[i + 1][j + 1] == 0 {
return false;
}
}
}
true
}
}func possibleToStamp(grid [][]int, stampHeight int, stampWidth int) bool {
m, n := len(grid), len(grid[0])
s := make([][]int, m+1)
d := make([][]int, m+1)
cnt := make([][]int, m+1)
for i := range s {
s[i] = make([]int, n+1)
d[i] = make([]int, n+1)
cnt[i] = make([]int, n+1)
}
for i, row := range grid {
for j, v := range row {
s[i+1][j+1] = s[i+1][j] + s[i][j+1] - s[i][j] + v
}
}
for i, row := range grid {
for j, v := range row {
if v == 0 {
x, y := i+stampHeight, j+stampWidth
if x <= m && y <= n && s[x][y]-s[i][y]-s[x][j]+s[i][j] == 0 {
d[i][j]++
d[i][y]--
d[x][j]--
d[x][y]++
}
}
}
}
for i, row := range grid {
for j, v := range row {
cnt[i+1][j+1] = cnt[i+1][j] + cnt[i][j+1] - cnt[i][j] + d[i][j]
if v == 0 && cnt[i+1][j+1] == 0 {
return false
}
}
}
return true
}/**
* @param {number[][]} grid
* @param {number} stampHeight
* @param {number} stampWidth
* @return {boolean}
*/
var possibleToStamp = function (grid, stampHeight, stampWidth) {
const m = grid.length;
const n = grid[0].length;
let s = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
let d = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
let cnt = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j];
}
}
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (grid[i][j] == 0) {
let [x, y] = [i + stampHeight, j + stampWidth];
if (
x <= m &&
y <= n &&
s[x][y] - s[i][y] - s[x][j] + s[i][j] == 0
) {
d[i][j]++;
d[i][y]--;
d[x][j]--;
d[x][y]++;
}
}
}
}
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
cnt[i + 1][j + 1] =
cnt[i + 1][j] + cnt[i][j + 1] - cnt[i][j] + d[i][j];
if (grid[i][j] == 0 && cnt[i + 1][j + 1] == 0) {
return false;
}
}
}
return true;
};