You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of n nodes numbered from 0 to n - 1 and exactly n - 1 edges. The root of the tree is the node 0, and each node of the tree has a label which is a lower-case character given in the string labels (i.e. The node with the number i has the label labels[i]).
The edges array is given on the form edges[i] = [ai, bi], which means there is an edge between nodes ai and bi in the tree.
Return an array of size n where ans[i] is the number of nodes in the subtree of the ith node which have the same label as node i.
A subtree of a tree T is the tree consisting of a node in T and all of its descendant nodes.
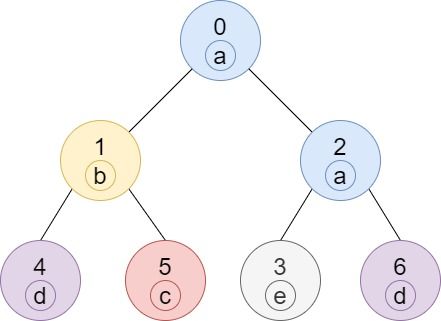
Example 1:
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd" Output: [2,1,1,1,1,1,1] Explanation: Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree. Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
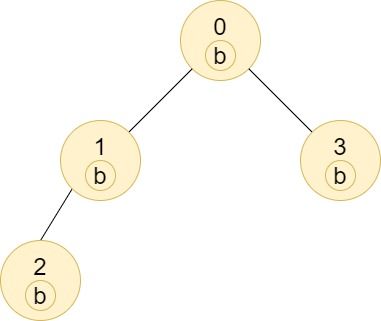
Example 2:
Input: n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb" Output: [4,2,1,1] Explanation: The sub-tree of node 2 contains only node 2, so the answer is 1. The sub-tree of node 3 contains only node 3, so the answer is 1. The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2. The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
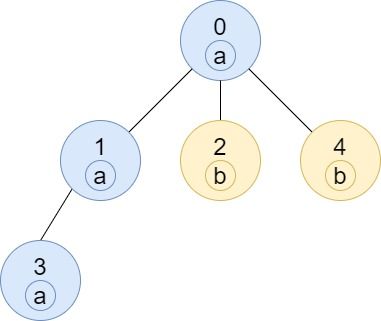
Example 3:
Input: n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab" Output: [3,2,1,1,1]
Constraints:
1 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != bilabels.length == nlabelsis consisting of only of lowercase English letters.
class Solution:
def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:
def dfs(i, fa):
ans[i] -= cnt[labels[i]]
cnt[labels[i]] += 1
for j in g[i]:
if j != fa:
dfs(j, i)
ans[i] += cnt[labels[i]]
g = defaultdict(list)
for a, b in edges:
g[a].append(b)
g[b].append(a)
cnt = Counter()
ans = [0] * n
dfs(0, -1)
return ansclass Solution {
private List<Integer>[] g;
private String labels;
private int[] ans;
private int[] cnt;
public int[] countSubTrees(int n, int[][] edges, String labels) {
g = new List[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (int[] e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
this.labels = labels;
ans = new int[n];
cnt = new int[26];
dfs(0, -1);
return ans;
}
private void dfs(int i, int fa) {
int k = labels.charAt(i) - 'a';
ans[i] -= cnt[k];
cnt[k]++;
for (int j : g[i]) {
if (j != fa) {
dfs(j, i);
}
}
ans[i] += cnt[k];
}
}class Solution {
public:
vector<int> countSubTrees(int n, vector<vector<int>>& edges, string labels) {
vector<vector<int>> g(n);
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
}
vector<int> ans(n);
int cnt[26]{};
function<void(int, int)> dfs = [&](int i, int fa) {
int k = labels[i] - 'a';
ans[i] -= cnt[k];
cnt[k]++;
for (int& j : g[i]) {
if (j != fa) {
dfs(j, i);
}
}
ans[i] += cnt[k];
};
dfs(0, -1);
return ans;
}
};func countSubTrees(n int, edges [][]int, labels string) []int {
g := make([][]int, n)
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
ans := make([]int, n)
cnt := [26]int{}
var dfs func(int, int)
dfs = func(i, fa int) {
k := labels[i] - 'a'
ans[i] -= cnt[k]
cnt[k]++
for _, j := range g[i] {
if j != fa {
dfs(j, i)
}
}
ans[i] += cnt[k]
}
dfs(0, -1)
return ans
}function countSubTrees(n: number, edges: number[][], labels: string): number[] {
const dfs = (i: number, fa: number) => {
const k = labels.charCodeAt(i) - 97;
ans[i] -= cnt[k];
cnt[k]++;
for (const j of g[i]) {
if (j !== fa) {
dfs(j, i);
}
}
ans[i] += cnt[k];
};
const ans = new Array(n).fill(0),
cnt = new Array(26).fill(0);
const g: number[][] = Array.from({ length: n }, () => []);
for (const [a, b] of edges) {
g[a].push(b);
g[b].push(a);
}
dfs(0, -1);
return ans;
}