A company has n employees with a unique ID for each employee from 0 to n - 1. The head of the company is the one with headID.
Each employee has one direct manager given in the manager array where manager[i] is the direct manager of the i-th employee, manager[headID] = -1. Also, it is guaranteed that the subordination relationships have a tree structure.
The head of the company wants to inform all the company employees of an urgent piece of news. He will inform his direct subordinates, and they will inform their subordinates, and so on until all employees know about the urgent news.
The i-th employee needs informTime[i] minutes to inform all of his direct subordinates (i.e., After informTime[i] minutes, all his direct subordinates can start spreading the news).
Return the number of minutes needed to inform all the employees about the urgent news.
Example 1:
Input: n = 1, headID = 0, manager = [-1], informTime = [0] Output: 0 Explanation: The head of the company is the only employee in the company.
Example 2:
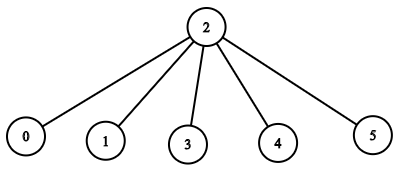
Input: n = 6, headID = 2, manager = [2,2,-1,2,2,2], informTime = [0,0,1,0,0,0] Output: 1 Explanation: The head of the company with id = 2 is the direct manager of all the employees in the company and needs 1 minute to inform them all. The tree structure of the employees in the company is shown.
Constraints:
1 <= n <= 1050 <= headID < nmanager.length == n0 <= manager[i] < nmanager[headID] == -1informTime.length == n0 <= informTime[i] <= 1000informTime[i] == 0if employeeihas no subordinates.- It is guaranteed that all the employees can be informed.
Solution 1: DFS
We first build an adjacent list
Next, we design a function
In function
The time complexity is
class Solution:
def numOfMinutes(
self, n: int, headID: int, manager: List[int], informTime: List[int]
) -> int:
def dfs(i: int) -> int:
ans = 0
for j in g[i]:
ans = max(ans, dfs(j) + informTime[i])
return ans
g = defaultdict(list)
for i, x in enumerate(manager):
g[x].append(i)
return dfs(headID)class Solution {
private List<Integer>[] g;
private int[] informTime;
public int numOfMinutes(int n, int headID, int[] manager, int[] informTime) {
g = new List[n];
Arrays.setAll(g, k -> new ArrayList<>());
this.informTime = informTime;
for (int i = 0; i < n; ++i) {
if (manager[i] >= 0) {
g[manager[i]].add(i);
}
}
return dfs(headID);
}
private int dfs(int i) {
int ans = 0;
for (int j : g[i]) {
ans = Math.max(ans, dfs(j) + informTime[i]);
}
return ans;
}
}class Solution {
public:
int numOfMinutes(int n, int headID, vector<int>& manager, vector<int>& informTime) {
vector<vector<int>> g(n);
for (int i = 0; i < n; ++i) {
if (manager[i] >= 0) {
g[manager[i]].push_back(i);
}
}
function<int(int)> dfs = [&](int i) -> int {
int ans = 0;
for (int j : g[i]) {
ans = max(ans, dfs(j) + informTime[i]);
}
return ans;
};
return dfs(headID);
}
};func numOfMinutes(n int, headID int, manager []int, informTime []int) int {
g := make([][]int, n)
for i, x := range manager {
if x != -1 {
g[x] = append(g[x], i)
}
}
var dfs func(int) int
dfs = func(i int) (ans int) {
for _, j := range g[i] {
ans = max(ans, dfs(j)+informTime[i])
}
return
}
return dfs(headID)
}
func max(a, b int) int {
if a > b {
return a
}
return b
}function numOfMinutes(
n: number,
headID: number,
manager: number[],
informTime: number[],
): number {
const g: number[][] = new Array(n).fill(0).map(() => []);
for (let i = 0; i < n; ++i) {
if (manager[i] !== -1) {
g[manager[i]].push(i);
}
}
const dfs = (i: number): number => {
let ans = 0;
for (const j of g[i]) {
ans = Math.max(ans, dfs(j) + informTime[i]);
}
return ans;
};
return dfs(headID);
}public class Solution {
private List<int>[] g;
private int[] informTime;
public int NumOfMinutes(int n, int headID, int[] manager, int[] informTime) {
g = new List<int>[n];
for (int i = 0; i < n; ++i) {
g[i] = new List<int>();
}
this.informTime = informTime;
for (int i = 0; i < n; ++i) {
if (manager[i] != -1) {
g[manager[i]].Add(i);
}
}
return dfs(headID);
}
private int dfs(int i) {
int ans = 0;
foreach (int j in g[i]) {
ans = Math.Max(ans, dfs(j) + informTime[i]);
}
return ans;
}
}