README_EN.md

1222. Queens That Can Attack the King

中文文档

Description

On a 0-indexed 8 x 8 chessboard, there can be multiple black queens ad one white king.

You are given a 2D integer array queens where queens[i] = [xQueeni, yQueeni] represents the position of the ith black queen on the chessboard. You are also given an integer array king of length 2 where king = [xKing, yKing] represents the position of the white king.

Return the coordinates of the black queens that can directly attack the king. You may return the answer in any order.

 

Example 1:

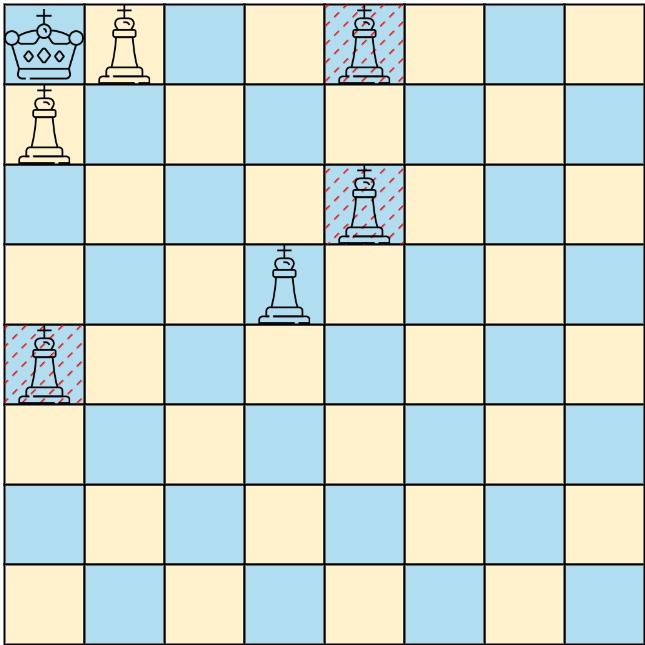
Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
Output: [[0,1],[1,0],[3,3]]
Explanation: The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).

Example 2:

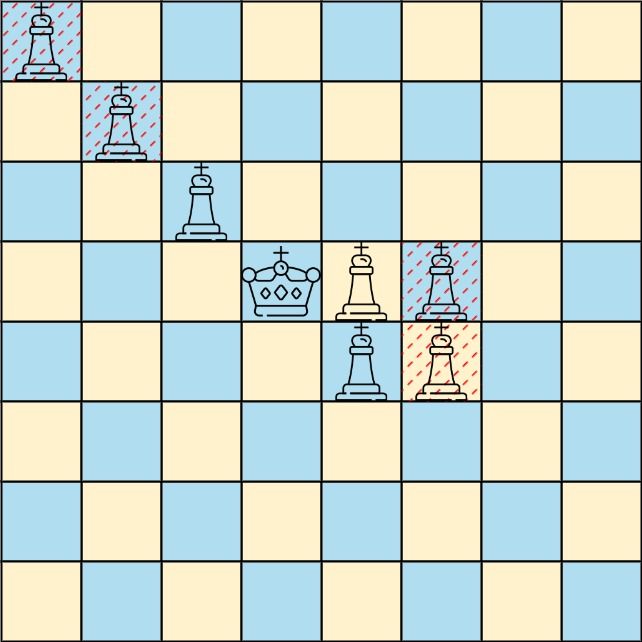
Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
Output: [[2,2],[3,4],[4,4]]
Explanation: The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).

 

Constraints:

• 1 <= queens.length < 64
• queens[i].length == king.length == 2
• 0 <= xQueeni, yQueeni, xKing, yKing < 8
• All the given positions are unique.

Solutions

Python3

class Solution:
    def queensAttacktheKing(
        self, queens: List[List[int]], king: List[int]
    ) -> List[List[int]]:
        n = 8
        s = {(i, j) for i, j in queens}
        ans = []
        for a, b in [
            [-1, 0],
            [1, 0],
            [0, -1],
            [0, 1],
            [1, 1],
            [1, -1],
            [-1, 1],
            [-1, -1],
        ]:
            x, y = king
            while 0 <= x + a < n and 0 <= y + b < n:
                x, y = x + a, y + b
                if (x, y) in s:
                    ans.append([x, y])
                    break
        return ans

Java

class Solution {
    private static final int N = 8;
    private int[][] dirs
        = new int[][] {{0, -1}, {0, 1}, {1, 0}, {-1, 0}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};

    public List<List<Integer>> queensAttacktheKing(int[][] queens, int[] king) {
        Set<Integer> s = get(queens);
        List<List<Integer>> ans = new ArrayList<>();
        for (int[] dir : dirs) {
            int x = king[0], y = king[1];
            int a = dir[0], b = dir[1];
            while (x + a >= 0 && x + a < N && y + b >= 0 && y + b < N) {
                x += a;
                y += b;
                if (s.contains(x * N + y)) {
                    ans.add(Arrays.asList(x, y));
                    break;
                }
            }
        }
        return ans;
    }

    private Set<Integer> get(int[][] queens) {
        Set<Integer> ans = new HashSet<>();
        for (int[] queen : queens) {
            ans.add(queen[0] * N + queen[1]);
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {
        unordered_set<int> s;
        int n = 8;
        for (auto& queen : queens) s.insert(queen[0] * n + queen[1]);
        vector<vector<int>> dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
        vector<vector<int>> ans;
        for (auto& dir : dirs) {
            int x = king[0], y = king[1];
            int a = dir[0], b = dir[1];
            while (x + a >= 0 && x + a < n && y + b >= 0 && y + b < n) {
                x += a;
                y += b;
                if (s.count(x * n + y)) {
                    ans.push_back({x, y});
                    break;
                }
            }
        }
        return ans;
    }
};

Go

func queensAttacktheKing(queens [][]int, king []int) [][]int {
	s := make(map[int]bool)
	n := 8
	for _, queen := range queens {
		s[queen[0]*n+queen[1]] = true
	}
	dirs := [8][2]int{{0, -1}, {0, 1}, {1, 0}, {-1, 0}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}}
	var ans [][]int
	for _, dir := range dirs {
		x, y := king[0], king[1]
		a, b := dir[0], dir[1]
		for x+a >= 0 && x+a < n && y+b >= 0 && y+b < n {
			x, y = x+a, y+b
			if s[x*n+y] {
				ans = append(ans, []int{x, y})
				break
			}
		}
	}
	return ans
}

...