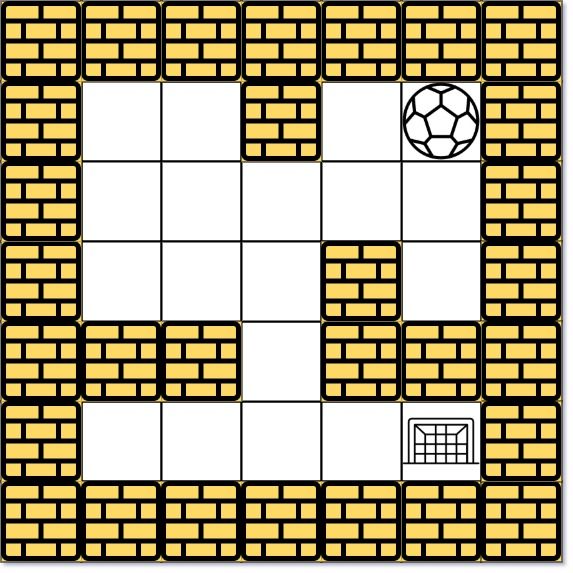
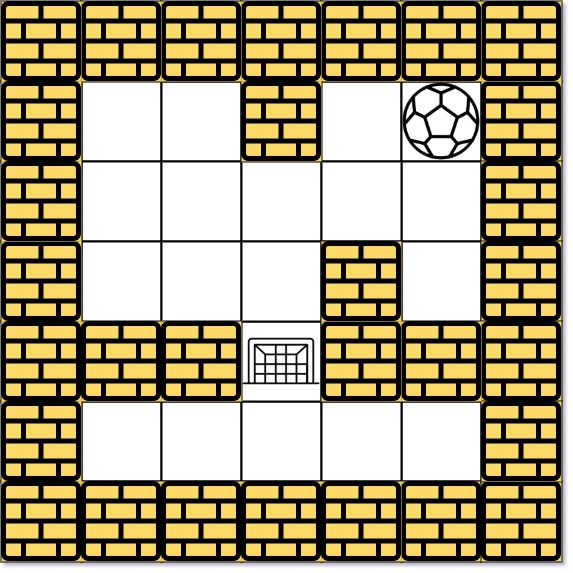
There is a ball in a maze with empty spaces (represented as 0) and walls (represented as 1). The ball can go through the empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.
Given the m x n maze, the ball's start position and the destination, where start = [startrow, startcol] and destination = [destinationrow, destinationcol], return true if the ball can stop at the destination, otherwise return false.
You may assume that the borders of the maze are all walls (see examples).
Example 1:
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [4,4] Output: true Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.
Example 2:
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [3,2] Output: false Explanation: There is no way for the ball to stop at the destination. Notice that you can pass through the destination but you cannot stop there.
Example 3:
Input: maze = [[0,0,0,0,0],[1,1,0,0,1],[0,0,0,0,0],[0,1,0,0,1],[0,1,0,0,0]], start = [4,3], destination = [0,1] Output: false
Constraints:
m == maze.lengthn == maze[i].length1 <= m, n <= 100maze[i][j]is0or1.start.length == 2destination.length == 20 <= startrow, destinationrow <= m0 <= startcol, destinationcol <= n- Both the ball and the destination exist in an empty space, and they will not be in the same position initially.
- The maze contains at least 2 empty spaces.
DFS.
class Solution:
def hasPath(
self, maze: List[List[int]], start: List[int], destination: List[int]
) -> bool:
def dfs(i, j):
if vis[i][j]:
return
vis[i][j] = True
if [i, j] == destination:
return
for a, b in [[0, -1], [0, 1], [1, 0], [-1, 0]]:
x, y = i, j
while 0 <= x + a < m and 0 <= y + b < n and maze[x + a][y + b] == 0:
x, y = x + a, y + b
dfs(x, y)
m, n = len(maze), len(maze[0])
vis = [[False] * n for _ in range(m)]
dfs(start[0], start[1])
return vis[destination[0]][destination[1]]BFS.
class Solution:
def hasPath(
self, maze: List[List[int]], start: List[int], destination: List[int]
) -> bool:
m, n = len(maze), len(maze[0])
q = deque([start])
rs, cs = start
vis = {(rs, cs)}
while q:
i, j = q.popleft()
for a, b in [[0, -1], [0, 1], [-1, 0], [1, 0]]:
x, y = i, j
while 0 <= x + a < m and 0 <= y + b < n and maze[x + a][y + b] == 0:
x, y = x + a, y + b
if [x, y] == destination:
return True
if (x, y) not in vis:
vis.add((x, y))
q.append((x, y))
return FalseDFS.
class Solution {
private boolean[][] vis;
private int[][] maze;
private int[] d;
private int m;
private int n;
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
m = maze.length;
n = maze[0].length;
d = destination;
this.maze = maze;
vis = new boolean[m][n];
dfs(start[0], start[1]);
return vis[d[0]][d[1]];
}
private void dfs(int i, int j) {
if (vis[i][j]) {
return;
}
vis[i][j] = true;
if (i == d[0] && j == d[1]) {
return;
}
int[] dirs = {-1, 0, 1, 0, -1};
for (int k = 0; k < 4; ++k) {
int x = i, y = j;
int a = dirs[k], b = dirs[k + 1];
while (x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && maze[x + a][y + b] == 0) {
x += a;
y += b;
}
dfs(x, y);
}
}
}BFS.
class Solution {
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
int m = maze.length;
int n = maze[0].length;
boolean[][] vis = new boolean[m][n];
vis[start[0]][start[1]] = true;
Deque<int[]> q = new LinkedList<>();
q.offer(start);
int[] dirs = {-1, 0, 1, 0, -1};
while (!q.isEmpty()) {
int[] p = q.poll();
int i = p[0], j = p[1];
for (int k = 0; k < 4; ++k) {
int x = i, y = j;
int a = dirs[k], b = dirs[k + 1];
while (
x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && maze[x + a][y + b] == 0) {
x += a;
y += b;
}
if (x == destination[0] && y == destination[1]) {
return true;
}
if (!vis[x][y]) {
vis[x][y] = true;
q.offer(new int[] {x, y});
}
}
}
return false;
}
}class Solution {
public:
vector<vector<int>> maze;
vector<vector<bool>> vis;
vector<int> d;
int m;
int n;
bool hasPath(vector<vector<int>>& maze, vector<int>& start, vector<int>& destination) {
m = maze.size();
n = maze[0].size();
d = destination;
vis.resize(m, vector<bool>(n, false));
this->maze = maze;
dfs(start[0], start[1]);
return vis[d[0]][d[1]];
}
void dfs(int i, int j) {
if (vis[i][j]) return;
vis[i][j] = true;
if (i == d[0] && j == d[1]) return;
vector<int> dirs = {-1, 0, 1, 0, -1};
for (int k = 0; k < 4; ++k) {
int x = i, y = j;
int a = dirs[k], b = dirs[k + 1];
while (x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && maze[x + a][y + b] == 0) {
x += a;
y += b;
}
dfs(x, y);
}
}
};class Solution {
public:
bool hasPath(vector<vector<int>>& maze, vector<int>& start, vector<int>& destination) {
int m = maze.size();
int n = maze[0].size();
queue<vector<int>> q{{start}};
vector<vector<bool>> vis(m, vector<bool>(n));
vis[start[0]][start[1]] = true;
vector<int> dirs = {-1, 0, 1, 0, -1};
while (!q.empty()) {
auto p = q.front();
q.pop();
int i = p[0], j = p[1];
for (int k = 0; k < 4; ++k) {
int x = i, y = j;
int a = dirs[k], b = dirs[k + 1];
while (x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && maze[x + a][y + b] == 0) {
x += a;
y += b;
}
if (x == destination[0] && y == destination[1]) return 1;
if (!vis[x][y]) {
vis[x][y] = true;
q.push({x, y});
}
}
}
return 0;
}
};func hasPath(maze [][]int, start []int, destination []int) bool {
m, n := len(maze), len(maze[0])
vis := make([][]bool, m)
for i := range vis {
vis[i] = make([]bool, n)
}
var dfs func(i, j int)
dfs = func(i, j int) {
if vis[i][j] {
return
}
vis[i][j] = true
if i == destination[0] && j == destination[1] {
return
}
dirs := []int{-1, 0, 1, 0, -1}
for k := 0; k < 4; k++ {
x, y := i, j
a, b := dirs[k], dirs[k+1]
for x+a >= 0 && x+a < m && y+b >= 0 && y+b < n && maze[x+a][y+b] == 0 {
x += a
y += b
}
dfs(x, y)
}
}
dfs(start[0], start[1])
return vis[destination[0]][destination[1]]
}func hasPath(maze [][]int, start []int, destination []int) bool {
m, n := len(maze), len(maze[0])
vis := make([][]bool, m)
for i := range vis {
vis[i] = make([]bool, n)
}
vis[start[0]][start[1]] = true
q := [][]int{start}
dirs := []int{-1, 0, 1, 0, -1}
for len(q) > 0 {
i, j := q[0][0], q[0][1]
q = q[1:]
for k := 0; k < 4; k++ {
x, y := i, j
a, b := dirs[k], dirs[k+1]
for x+a >= 0 && x+a < m && y+b >= 0 && y+b < n && maze[x+a][y+b] == 0 {
x += a
y += b
}
if x == destination[0] && y == destination[1] {
return true
}
if !vis[x][y] {
vis[x][y] = true
q = append(q, []int{x, y})
}
}
}
return false
}