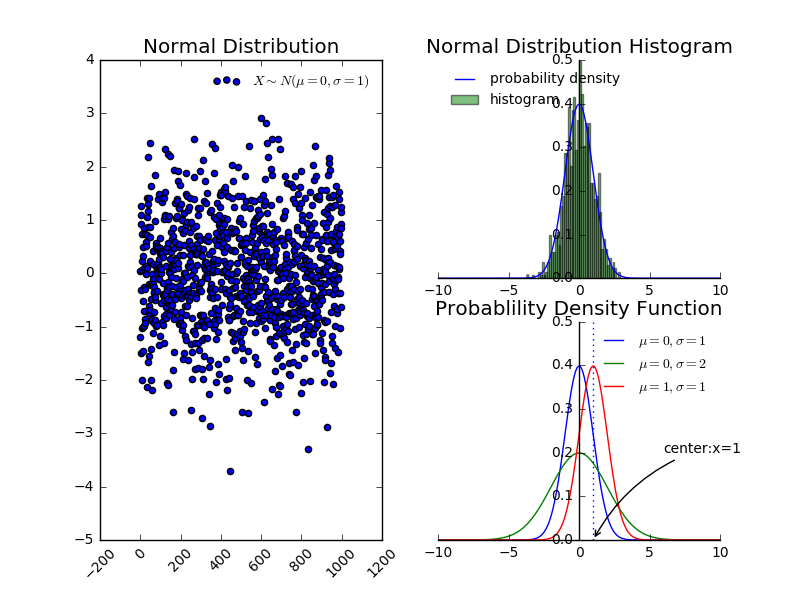
正态分布只依赖于数据集的两个特征:样本的均值和方差。正态分布的这种统计特性使得问题变得异常简单,任何具有正态分布的变量,都可以进行高精度分预测。值得注意的是,大自然中发现的变量,大多近似服从正态分布。即如果某个随机变量取值范围是实数,且对它的概率分布一无所知,通常会假设它服从正态分布,其考量的原因包括:
设 $X \sim N(\mu,\sigma^2)$,则其概率密度为:
$$
f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}, -\infty<x<\infty
$$
其中 $\mu, \sigma(\sigma>0)$ 为常数,若随机变量 $X$ 的概率密度函数如上所述,则称 $X$ 服从参数为 $\mu, \sigma$ 的正态分布或者高斯分布,记作 $X \sim N\left(\mu, \sigma^{2}\right)$。
当 $\mu=0, \sigma=1$ 时,称为标准正态分布,其概率密度函数记作 $\varphi(x)$,分布函数记作 $\Phi(x)$。为了方便计算,有时记作 $\mathcal{N}\left(x ; \mu, \beta^{-1}\right)=\sqrt{\frac{\beta}{2 \pi}} \exp \left(-\frac{1}{2} \beta(x-\mu)^{2}\right)$,其中 $\beta \in(0, \infty)$。
正态分布的概率密度函数性质如下:
- 曲线关于 $x = \mu$ 处对称,并且在该处取到最大值。
- 曲线在 $x=\mu \pm \sigma$ 处有拐点,参数 $\mu$ 决定曲线的位置,$\sigma$ 决定图形的胖瘦。
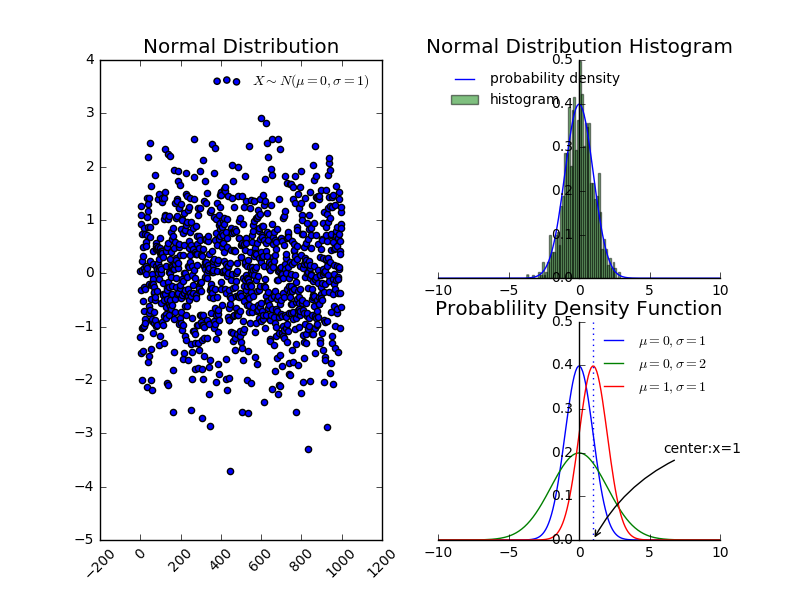
若 $X \sim N\left(\mu, \sigma^{2}\right)$ 则称 $\frac{X-\mu}{\sigma} \sim N(0,1)$,其期望 $\mathbb{E}[X]=\mu$,方差 $\operatorname{Var}[X]=\sigma^{2}$。
有限个相互独立的正态随机变量的线性组合仍然服从正态分布:若随机变量 $X_{i} \sim N\left(\mu_{i}, \sigma_{i}^{2}\right), i=1,2, \cdots, n$,且它们相互独立,则它们的线性组合:$C_{1} X_{1}+C_{2} X_{2}+\cdots+C_{n} X_{n}$ 仍然服从正态分布(其中 $C_{1}, C_{2}, \cdots, C_{n}$ 不全是为 0 的常数),且 $C_{1} X_{1}+C_{2} X_{2}+\cdots+C_{n} X_{n} \sim N\left(\sum_{i=1}^{n} C_{i} \mu_{i}, \sum_{i=1}^{n} C_{i}^{2} \sigma_{i}^{2}\right)$。
https://parg.co/NOA 5.4 节
二维正态随机变量 $(X,Y)$ 的概率密度为:
$$
\begin{aligned} p(x, y) &=\frac{1}{2 \pi \sigma_{1} \sigma_{2} \sqrt{1-\rho^{2}}} \exp \left{\frac{-1}{2\left(1-\rho^{2}\right)}\left[\frac{\left(x-\mu_{1}\right)^{2}}{\sigma_{1}^{2}}\right.\right.\ &-2 \rho \frac{\left(x-\mu_{1}\right)\left(y-\mu_{2}\right)}{\sigma_{1} \sigma_{2}}+\frac{\left(y-\mu_{2}\right)^{2}}{\sigma_{2}^{2}} ] } \end{aligned}
$$
根据定义,可以计算出:
$$
p_{X}(x)=\frac{1}{\sqrt{2 \pi} \sigma_{1}} e^{-\left(x-\mu_{1}\right)^{2} /\left(2 \sigma_{1}^{2}\right)},-\infty<x<\infty \\
p_{Y}(y)=\frac{1}{\sqrt{2 \pi} \sigma_{2}} e^{-\left(y-\mu_{2}\right)^{2} /\left(2 \sigma_{2}^{2}\right)},-\infty<y<\infty \\
$$
$$
\begin{array}{c}{\mathbb{E}[X]=\mu_{1}} \ {\mathbb{E}[Y]=\mu_{2}} \ {\operatorname{Var}[X]=\sigma_{1}^{2}} \ {\operatorname{Var}[Y]=\sigma_{2}^{2}} \ {\operatorname{Cov}[X, Y]=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}\left(x-\mu_{1}\right)\left(y-\mu_{2}\right) p(x, y) d x d y=\rho \sigma_{1} \sigma_{2}} \ {\rho_{X Y}=\rho}\end{array}
$$
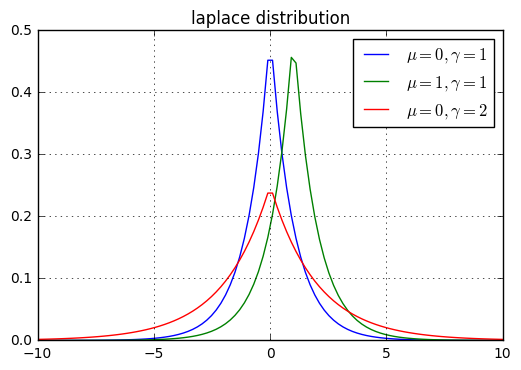
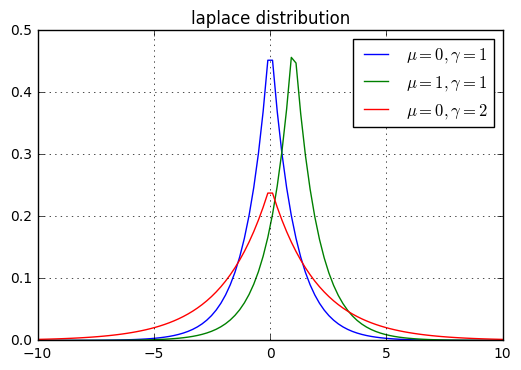
拉普拉斯分布的概率密度函数为:
$$
p(x ; \mu, \gamma)=\frac{1}{2 \gamma} \exp \left(-\frac{|x-\mu|}{\gamma}\right)
$$
其期望为 $\mathbb{E}[X]=\mu$,方差为 $\operatorname{Var}[X]=2 \gamma^{2}$。