给你一个大小为 m x n 的整数矩阵 isWater ,它代表了一个由 陆地 和 水域 单元格组成的地图。
- 如果
isWater[i][j] == 0,格子(i, j)是一个 陆地 格子。 - 如果
isWater[i][j] == 1,格子(i, j)是一个 水域 格子。
你需要按照如下规则给每个单元格安排高度:
- 每个格子的高度都必须是非负的。
- 如果一个格子是 水域 ,那么它的高度必须为
0。 - 任意相邻的格子高度差 至多 为
1。当两个格子在正东、南、西、北方向上相互紧挨着,就称它们为相邻的格子。(也就是说它们有一条公共边)
找到一种安排高度的方案,使得矩阵中的最高高度值 最大 。
请你返回一个大小为 m x n 的整数矩阵 height ,其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法,请返回 任意一个 。
示例 1:
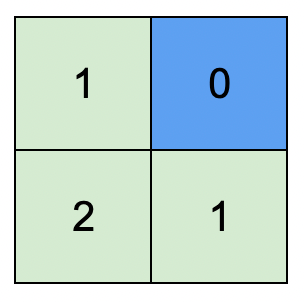
输入:isWater = [[0,1],[0,0]] 输出:[[1,0],[2,1]] 解释:上图展示了给各个格子安排的高度。 蓝色格子是水域格,绿色格子是陆地格。
示例 2:
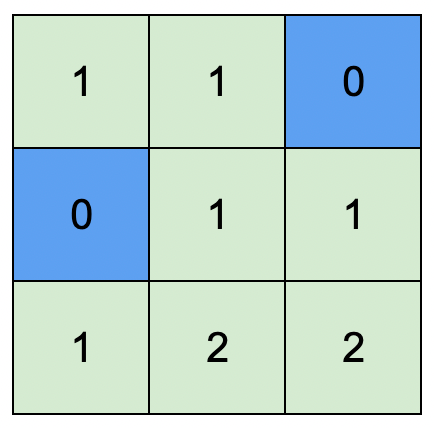
输入:isWater = [[0,0,1],[1,0,0],[0,0,0]] 输出:[[1,1,0],[0,1,1],[1,2,2]] 解释:所有安排方案中,最高可行高度为 2 。 任意安排方案中,只要最高高度为 2 且符合上述规则的,都为可行方案。
提示:
m == isWater.lengthn == isWater[i].length1 <= m, n <= 1000isWater[i][j]要么是0,要么是1。- 至少有 1 个水域格子。
多源 BFS。
class Solution:
def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:
m, n = len(isWater), len(isWater[0])
ans = [[-1] * n for _ in range(m)]
q = deque()
for i in range(m):
for j in range(n):
if isWater[i][j] == 1:
ans[i][j] = 0
q.append((i, j))
while q:
i, j = q.popleft()
for a, b in [[0, -1], [0, 1], [1, 0], [-1, 0]]:
x, y = i + a, j + b
if 0 <= x < m and 0 <= y < n and ans[x][y] == -1:
ans[x][y] = ans[i][j] + 1
q.append((x, y))
return ansclass Solution {
private int[][] dirs = new int[][]{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public int[][] highestPeak(int[][] isWater) {
int m = isWater.length, n = isWater[0].length;
int[][] ans = new int[m][n];
for (int i = 0; i < m; ++i) {
Arrays.fill(ans[i], -1);
}
Deque<int[]> q = new LinkedList<>();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (isWater[i][j] == 1) {
ans[i][j] = 0;
q.offerLast(new int[]{i, j});
}
}
}
while (!q.isEmpty()) {
int[] p = q.pollFirst();
int i = p[0], j = p[1];
for (int[] dir : dirs) {
int x = i + dir[0], y = j + dir[1];
if (x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1) {
ans[x][y] = ans[i][j] + 1;
q.offerLast(new int[]{x, y});
}
}
}
return ans;
}
}function highestPeak(isWater: number[][]): number[][] {
const m = isWater.length,
n = isWater[0].length;
let ans: Array<Array<number>> = Array.from({ length: m }, v =>
new Array(n).fill(-1),
);
// BFS
let queue: Array<Array<number>> = []; // i, j, num
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (isWater[i][j]) {
ans[i][j] = 0;
queue.push([i, j, 0]);
}
}
}
const directions = [
[0, -1],
[-1, 0],
[0, 1],
[1, 0],
]; // left, up, right, down
while (queue.length) {
// 消除push/shift出现超时问题
let tmp: Array<Array<number>> = [];
for (const [i, j, num] of queue) {
for (const [dx, dy] of directions) {
const x = i + dx,
y = j + dy;
// 校验合法的相邻格子
if (x > -1 && x < m && y > -1 && y < n && ans[x][y] == -1) {
ans[x][y] = num + 1;
tmp.push([x, y, num + 1]);
}
}
}
queue = tmp;
}
return ans;
}typedef pair<int, int> PII;
class Solution {
public:
vector<vector<int>> dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {
int m = isWater.size(), n = isWater[0].size();
vector<vector<int>> ans(m, vector<int>(n, -1));
queue<PII> q;
for (int i = 0; i < m; ++i)
{
for (int j = 0; j < n; ++j)
{
if (isWater[i][j] == 1)
{
ans[i][j] = 0;
q.push({i, j});
}
}
}
while (!q.empty())
{
PII p = q.front();
q.pop();
int i = p.first, j = p.second;
for (auto& dir : dirs)
{
int x = i + dir[0], y = j + dir[1];
if (x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1)
{
ans[x][y] = ans[i][j] + 1;
q.push({x, y});
}
}
}
return ans;
}
};func highestPeak(isWater [][]int) [][]int {
m, n := len(isWater), len(isWater[0])
ans := make([][]int, m)
for i := range ans {
ans[i] = make([]int, n)
for j := range ans[i] {
ans[i][j] = -1
}
}
type pair struct{ i, j int }
var q []pair
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if isWater[i][j] == 1 {
ans[i][j] = 0
q = append(q, pair{i, j})
}
}
}
dirs := [4][2]int{{0, -1}, {0, 1}, {1, 0}, {-1, 0}}
for len(q) > 0 {
p := q[0]
q = q[1:]
for _, dir := range dirs {
x, y := p.i+dir[0], p.j+dir[1]
if x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1 {
ans[x][y] = ans[p.i][p.j] + 1
q = append(q, pair{x, y})
}
}
}
return ans
}