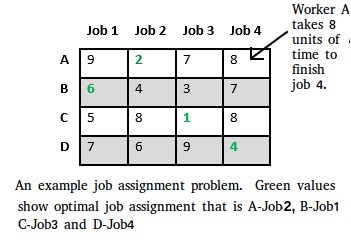
Let there be N workers and N jobs. Any worker can be assigned to perform any job, incurring some cost that may vary depending on the work-job assignment. It is required to perform all jobs by assigning exactly one worker to each job and exactly one job to each agent in such a way that the total cost of the assignment is minimized.
/* findMinCost uses Least() and Add() to maintain the
list of live nodes
Least() finds a live node with least cost, deletes
it from the list and returns it
Add(x) calculates cost of x and adds it to the list
of live nodes
Implements list of live nodes as a min heap */
// Search Space Tree Node
node
{
int job_number;
int worker_number;
node parent;
int cost;
}
// Input: Cost Matrix of Job Assignment problem
// Output: Optimal cost and Assignment of Jobs
algorithm findMinCost (costMatrix mat[][])
{
// Initialize list of live nodes(min-Heap)
// with root of search tree i.e. a Dummy node
while (true)
{
// Find a live node with least estimated cost
E = Least();
// The found node is deleted from the list
// of live nodes
if (E is a leaf node)
{
printSolution();
return;
}
for each child x of E
{
Add(x); // Add x to list of live nodes;
x->parent = E; // Pointer for path to root
}
}
}
// Program to solve Job Assignment problem
// using Branch and Bound
#include <bits/stdc++.h>
using namespace std;
#define N 4
// state space tree node
struct Node
{
// stores parent node of current node
// helps in tracing path when answer is found
Node* parent;
// contains cost for ancestors nodes
// including current node
int pathCost;
// contains least promising cost
int cost;
// contain worker number
int workerID;
// contains Job ID
int jobID;
// Boolean array assigned will contains
// info about available jobs
bool assigned[N];
};
// Function to allocate a new search tree node
// Here Person x is assigned to job y
Node* newNode(int x, int y, bool assigned[],
Node* parent)
{
Node* node = new Node;
for (int j = 0; j < N; j++)
node->assigned[j] = assigned[j];
node->assigned[y] = true;
node->parent = parent;
node->workerID = x;
node->jobID = y;
return node;
}
// Function to calculate the least promising cost
// of node after worker x is assigned to job y.
int calculateCost(int costMatrix[N][N], int x,
int y, bool assigned[])
{
int cost = 0;
// to store unavailable jobs
bool available[N] = {true};
// start from next worker
for (int i = x + 1; i < N; i++)
{
int min = INT_MAX, minIndex = -1;
// do for each job
for (int j = 0; j < N; j++)
{
// if job is unassigned
if (!assigned[j] && available[j] &&
costMatrix[i][j] < min)
{
// store job number
minIndex = j;
// store cost
min = costMatrix[i][j];
}
}
// add cost of next worker
cost += min;
// job becomes unavailable
available[minIndex] = false;
}
return cost;
}
// Comparison object to be used to order the heap
struct comp
{
bool operator()(const Node* lhs,
const Node* rhs) const
{
return lhs->cost > rhs->cost;
}
};
// print Assignments
void printAssignments(Node *min)
{
if(min->parent==NULL)
return;
printAssignments(min->parent);
cout << "Assign Worker " << char(min->workerID + 'A')
<< " to Job " << min->jobID << endl;
}
// Finds minimum cost using Branch and Bound.
int findMinCost(int costMatrix[N][N])
{
// Create a priority queue to store live nodes of
// search tree;
priority_queue<Node*, std::vector<Node*>, comp> pq;
// initialize heap to dummy node with cost 0
bool assigned[N] = {false};
Node* root = newNode(-1, -1, assigned, NULL);
root->pathCost = root->cost = 0;
root->workerID = -1;
// Add dummy node to list of live nodes;
pq.push(root);
// Finds a live node with least cost,
// add its childrens to list of live nodes and
// finally deletes it from the list.
while (!pq.empty())
{
// Find a live node with least estimated cost
Node* min = pq.top();
// The found node is deleted from the list of
// live nodes
pq.pop();
// i stores next worker
int i = min->workerID + 1;
// if all workers are assigned a job
if (i == N)
{
printAssignments(min);
return min->cost;
}
// do for each job
for (int j = 0; j < N; j++)
{
// If unassigned
if (!min->assigned[j])
{
// create a new tree node
Node* child = newNode(i, j, min->assigned, min);
// cost for ancestors nodes including current node
child->pathCost = min->pathCost + costMatrix[i][j];
// calculate its lower bound
child->cost = child->pathCost +
calculateCost(costMatrix, i, j, child->assigned);
// Add child to list of live nodes;
pq.push(child);
}
}
}
}
// Driver code
int main()
{
// x-coordinate represents a Worker
// y-coordinate represents a Job
int costMatrix[N][N] =
{
{9, 2, 7, 8},
{6, 4, 3, 7},
{5, 8, 1, 8},
{7, 6, 9, 4}
};
/* int costMatrix[N][N] =
{
{82, 83, 69, 92},
{77, 37, 49, 92},
{11, 69, 5, 86},
{ 8, 9, 98, 23}
};
*/
/* int costMatrix[N][N] =
{
{2500, 4000, 3500},
{4000, 6000, 3500},
{2000, 4000, 2500}
};*/
/*int costMatrix[N][N] =
{
{90, 75, 75, 80},
{30, 85, 55, 65},
{125, 95, 90, 105},
{45, 110, 95, 115}
};*/
cout << "\nOptimal Cost is "
<< findMinCost(costMatrix);
return 0;
}
Output
Assign Worker A to Job 1
Assign Worker B to Job 0
Assign Worker C to Job 2
Assign Worker D to Job 3
Optimal Cost is 13