| title | tags | authors | affiliations | date | codeRepository | license | bibliography | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
`bwsample`: Processing Best-Worst Scaling data |
|
|
|
13 March 2021 |
Apache-2.0 |
paper.bib |
bwsample is a Python package that provides algorithms to sample best-worst scaling sets (BWS sets), extract and count pairwise comparisons from user-evaluated BWS sets, and compute rankings and scores.
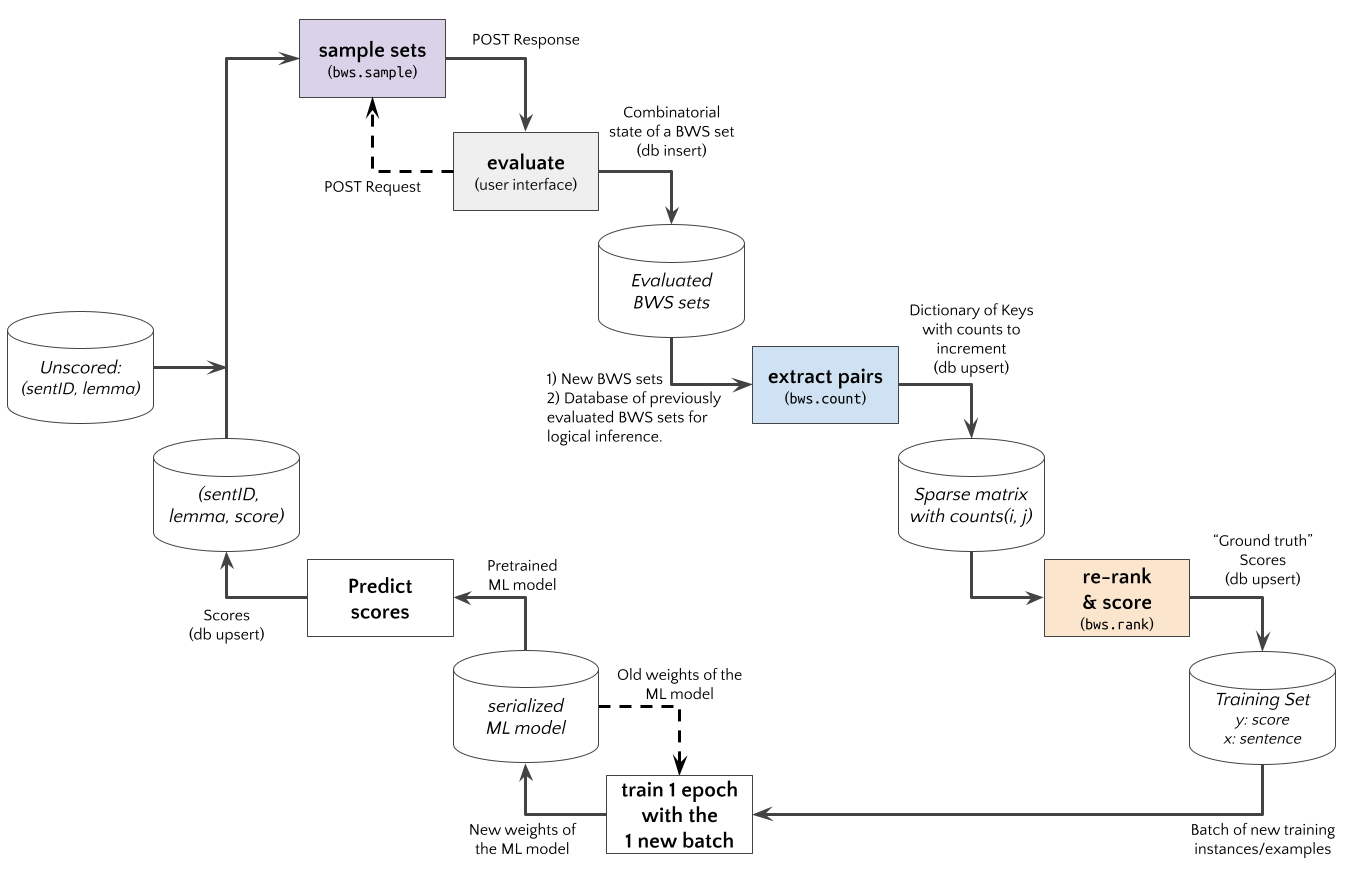
We are using the bwsample package as part of an Active Learning experiment in which linguistics experts and lay people (crowdsourcing) judge sentences examples with the Best-Worst Scaling (BWS) method (Fig. \ref{fig:active-learning-process}).
BWS is "... the cognitive process by which respondents repeatedly choose the two objects in varying sets of three or more objects that they feel exhibit the largest perceptual difference on an underlying continuum of interest" [@finn1992, p.13].
In our context, BWS is primarily used as a means of data collection that is more economically efficient than using pairwise comparison user interfaces [@hamster223a].
The sampling algorithms ensure overlapping BWS sets, and are deployed in the REST API for a Web App. Overlaps are required for counting pairs by logical inference [@hamster223a]. A possible question is how many items have to be shown twice a) initially, and b) after the pair frequency database grew over time to gather reasonable amounts of counting or resp. frequency data? The implemented counting algorithms can distinguish between 3 types of directly extract pairs and 7 types of logically inferred pairs. This creates an opportunity for further analysis, e.g., to detect inconsistent evaluations [@hamster223a], or to assign weights to different types of pairs. To compute rank items from pairwise comparison data, five algorithms are available: a) Eigenvector estimation of the reciprocal pairwise comparison matrix as scores [@saaty2003], b) MLE estimation of the Bradley-Terry-Luce probability model [@hunter2004, pp. 386-387], c) Simple ratios for each pair and sum the ratios for each item, d) Chi-Squared based p-value for each pair and sum 1 minus p-values for each item, and e) Estimation of the transition probability that the next element is better. All ranking algorithms are implemented based on sparse matrix operations.
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - 433249742.
bwsample is written in Python 3.6+ [@python3] and uses the following software packages:
NumPy, https://github.com/numpy/numpy [@numpy]SciPy, https://github.com/scipy/scipy [@scipy]scikit-learn, https://github.com/scikit-learn/scikit-learn [@scikit-learn]