0_Intro_OT.py

# coding: utf-8

# # Introduction to Optimal Transport with Python
# 
# #### *Rémi Flamary, Nicolas Courty*

# ## POT installation

# + Install with pip:
# ```bash
# pip install pot
# ```
# + Install with conda
# ```bash
# conda install -c conda-forge pot
# ```

# ## POT Python Optimal Transport Toolbox
# 
# #### Import the toolbox

# In[1]:


import numpy as np # always need it
import scipy as sp # often use it
import pylab as pl # do the plots

import ot # ot 


#%% #### Getting help
# 
# Online  documentation : [http://pot.readthedocs.io](http://pot.readthedocs.io) 
# 
# Or inline help:
# 

# In[2]:


help(ot.dist)


#%% ## First OT Problem
# 
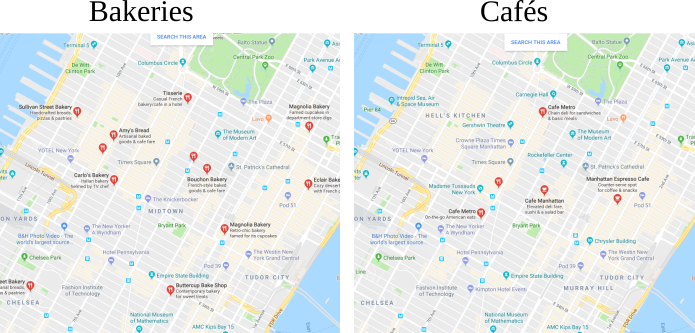
# We will solve the Bakery/Cafés problem of transporting croissants from a number of Bakeries to Cafés in a City (In this case Manhattan). We did a quick google map search in Manhattan for bakeries and Cafés:
# 
# ![bak.png](https://remi.flamary.com/cours/otml/bak.png)
# 
# We extracted from this search their positions and generated fictional production and sale number (that both sum to the same value).
# 
# We have acess to the position of Bakeries ```bakery_pos``` and their respective production ```bakery_prod``` which describe the source distribution. The Cafés where the croissants are sold are defiend also by their position ```cafe_pos``` and ```cafe_prod```. For fun we also provide a map ```Imap``` that will illustrate the position of these shops in the city.
# 
# 
# Now we load the data
# 
# 

# In[3]:


data=np.load('data/manhattan.npz')

bakery_pos=data['bakery_pos']
bakery_prod=data['bakery_prod']
cafe_pos=data['cafe_pos']
cafe_prod=data['cafe_prod']
Imap=data['Imap']

print('Bakery production: {}'.format(bakery_prod))
print('Cafe sale: {}'.format(cafe_prod))
print('Total croissants : {}'.format(cafe_prod.sum()))


#%% #### Plotting bakeries in the city
# 
# Next we plot the position of the bakeries and cafés on the map. The size of the circle is proportional to their production.
# 

# In[4]:



pl.figure(1,(8,7))
pl.clf()
pl.imshow(Imap,interpolation='bilinear') # plot the map
pl.scatter(bakery_pos[:,0],bakery_pos[:,1],s=bakery_prod,c='r', edgecolors='k',label='Bakeries')
pl.scatter(cafe_pos[:,0],cafe_pos[:,1],s=cafe_prod,c='b', edgecolors='k',label='Cafés')
pl.legend()
pl.title('Manhattan Bakeries and Cafés');


#%% #### Cost matrix
# 
# 
# We compute the cost matrix between the bakeries and the cafés, this will be the transport cost matrix. This can be done using the [ot.dist](http://pot.readthedocs.io/en/stable/all.html#ot.dist) that defaults to squared euclidean distance but can return other things such as cityblock (or manhattan distance). 
# 
# 

#%% #### Solving the OT problem with [ot.emd](http://pot.readthedocs.io/en/stable/all.html#ot.emd)

# #### Transportation plan vizualization
# 
# A good vizualization of the OT matrix in the 2D plane is to denote the transportation of mass between a Bakery and a Café by a line. This can easily be done with a double ```for``` loop.
# 
# In order to make it more interpretable one can also use the ```alpha``` parameter of plot and set it to ```alpha=G[i,j]/G[i,j].max()```. 

#%% #### OT loss and dual variables
# 
# The resulting wasserstein loss loss is of the form:
# 
# $W=\sum_{i,j}\gamma_{i,j}C_{i,j}$
# 
# where $\gamma$ is the optimal transport matrix.
# 

#%% #### Regularized OT with SInkhorn
# 
# The Sinkhorn algorithm is very simple to code. You can implement it directly using the following pseudo-code:
# 
# ![sinkhorn.png](attachment:sinkhorn.png)
# 
# An alternative is to use the POT toolbox with [ot.sinkhorn](http://pot.readthedocs.io/en/stable/all.html#ot.sinkhorn)
# 
# Be carefull to numerical problems. A good pre-provcessing for Sinkhorn is to divide the cost matrix ```C```
#  by its maximum value.