We read every piece of feedback, and take your input very seriously.
To see all available qualifiers, see our documentation.
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
图形变换与线性代数息息相关(坐标系空间转换), 坐标变换与矩阵变换。在笛卡尔坐标系中,每个 欧氏空间 里的点都由横坐标和纵坐标这两个值来确定。在 CSS(和大部分的计算机图形学)中,原点 (0, 0) 在元素的左上角。每个点都使用数学上的向量符号 (x, y) 来描述。
欧氏空间
CSS
(0, 0)
(x, y)
每个线性函数使用 2 × 2 矩阵描述,如:
[a c] [b d]
将矩阵乘法用于上述坐标系中的每个点,一个变换就形成了:
可以在一行中进行多次矩阵乘法进行变换:
有了这种方法,就可以描述大部分常见的变换,并因此可以将他们组合起来,如:旋转、缩放或拉伸。事实上,所有线性函数的变换都可以被描述,组合的变换是从右到左生效的。然而,有一种常见的变换并不是线性的,所以当这种变换要用这种方法来表示时,应该被单独列出来:位移。位移的向量 (tx, ty) 必须单独表示,作为两个附加参数, 那我们描述矩阵会变成如下展示:
(tx, ty)
| a c tx | | b d tx | | 0 0 1 |
显而易见 transform 的属性是由 Matrix 矩阵通过参数计算出来
在 2D变换中,矩阵变换函数 matrix() 接受 6 个值,语法形式如下:
matrix()
matrix(a, b, c, d, e, f)
在 齐次坐标 下相当于变换矩阵:
| a c e | | b d f | | 0 0 1 |
变换矩阵,如何进行线性坐标变换呢?设元素所呈现出来的几何图形中一点的坐标是 (x, y),那么所谓的根据变换矩阵进行变换就是使用这个点的坐标 (x, y) 的向量矩阵:
[x y 1 ]
与变换矩阵相乘:
在 2D变换中,变换总共有以下几种操作:
transform: translate(X, Y)
transform: rotate(θ)
transform: skew(α, β)
transform: scale(scaleX, scaleY)
这些对应的变换矩阵分别如下:
平移变换 translate(X, Y),相当于对其应用如下变换矩阵:
translate(X, Y)
| 1 0 X | | 0 1 Y | | 0 0 1 |
即等价于使用矩阵变换函数 matrix(1, 0, 0, 1, X, Y)。
matrix(1, 0, 0, 1, X, Y)
旋转变换 rotate(θ),相当于对其应用如下变换矩阵:
rotate(θ)
| cosθ −sinθ 0 | | sinθ cosθ 0 | | 0 0 1 |
即等价于矩阵变换函数 matrix(cosθ, sinθ, -sinθ, cosθ, 0, 0)。
matrix(cosθ, sinθ, -sinθ, cosθ, 0, 0)
倾斜变换 skew(α, β),相当于对其应用如下变换矩阵:
skew(α, β)
| 1 tanα 0 | | tanβ 1 0 | | 0 0 1 |
即等价于使用矩阵变换函数 matrix(1, tanβ, tanα, 1, 0, 0)。
matrix(1, tanβ, tanα, 1, 0, 0)
缩放变换 scale(scaleX, scaleY),相当于对其应用如下变换矩阵:
scale(scaleX, scaleY)
| scaleX 0 0 | | 0 scaleY 0 | | 0 0 1 |
即等价于使用矩阵变换函数 matrix(scaleX, 0, 0, scaleY, 0, 0)。
matrix(scaleX, 0, 0, scaleY, 0, 0)
在 3D变换中,矩阵变换函数 matrix3d() 接受 16 个值,语法形式如下:
matrix3d()
matrix3d(a1, b1, c1, d1, a2, b2, c2, d2, a3, b3, c3, d3, a4, b4, c4, d4)
注意: matrix(a, b, c, d, e, f) 是 matrix3d(a, b, 0, 0, c, d, 0, 0, 0, 0, 1, 0, e, f, 0, 1) 的一个简写
matrix3d(a, b, 0, 0, c, d, 0, 0, 0, 0, 1, 0, e, f, 0, 1)
| a1 a2 a3 a4 | | b1 b2 b3 b4 | | c1 c2 c3 c4 | | d1 d2 d3 d4 |
3D 矩阵坐标变换
在 3D变换中,变换总共有以下几种操作:
transform: translate3d(X, Y, Z)
transform: rotate3d(X, Y, Z, θ)
transform: scale3d(scaleX, scaleY, scaleZ)
平移变换 translate3d(X, Y, Z),相当于对其应用如下变换矩阵:
translate3d(X, Y, Z)
| 1 0 0 X | | 0 1 0 Y | | 0 0 1 Z | | 0 0 0 1 |
即等价于使用矩阵变换函数 matrix3d(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, X, Y, Z, 1)。
matrix3d(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, X, Y, Z, 1)
旋转变换 rotate3d(x, y, z, α),相当于对其应用如下变换矩阵:
rotate3d(x, y, z, α)
缩放变换 scale3d(scaleX, scaleY, scaleZ),相当于对其应用如下变换矩阵:
scale3d(scaleX, scaleY, scaleZ)
| scaleX 0 0 0 | | 0 scaleY 0 0 | | 0 0 scaleZ 0 | | 0 0 0 1 |
即等价于使用矩阵变换函数 matrix3d(scaleX, 0, 0, 0, 0, scaleY, 0, 0, 0, 0, scaleZ, 0, 0, 0, 0, 1)。
matrix3d(scaleX, 0, 0, 0, 0, scaleY, 0, 0, 0, 0, scaleZ, 0, 0, 0, 0, 1)
理解矩阵乘法
Transform Functions
笛卡尔坐标系
3D数学基础-向量运算基础和矩阵变换
The text was updated successfully, but these errors were encountered:
No branches or pull requests
图形变换与线性代数息息相关(坐标系空间转换), 坐标变换与矩阵变换。在笛卡尔坐标系中,每个
欧氏空间里的点都由横坐标和纵坐标这两个值来确定。在CSS(和大部分的计算机图形学)中,原点(0, 0)在元素的左上角。每个点都使用数学上的向量符号(x, y)来描述。每个线性函数使用 2 × 2 矩阵描述,如:
将矩阵乘法用于上述坐标系中的每个点,一个变换就形成了:
可以在一行中进行多次矩阵乘法进行变换:
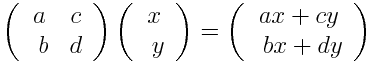
有了这种方法,就可以描述大部分常见的变换,并因此可以将他们组合起来,如:旋转、缩放或拉伸。事实上,所有线性函数的变换都可以被描述,组合的变换是从右到左生效的。然而,有一种常见的变换并不是线性的,所以当这种变换要用这种方法来表示时,应该被单独列出来:位移。位移的向量
(tx, ty)必须单独表示,作为两个附加参数, 那我们描述矩阵会变成如下展示:2D变换 matrix()
在 2D变换中,矩阵变换函数
matrix()接受 6 个值,语法形式如下:在 齐次坐标 下相当于变换矩阵:
变换矩阵,如何进行线性坐标变换呢?设元素所呈现出来的几何图形中一点的坐标是
(x, y),那么所谓的根据变换矩阵进行变换就是使用这个点的坐标(x, y)的向量矩阵:[x y 1 ]与变换矩阵相乘:
在 2D变换中,变换总共有以下几种操作:
transform: translate(X, Y)transform: rotate(θ)transform: skew(α, β)transform: scale(scaleX, scaleY)这些对应的变换矩阵分别如下:
平移 translate
平移变换
translate(X, Y),相当于对其应用如下变换矩阵:即等价于使用矩阵变换函数
matrix(1, 0, 0, 1, X, Y)。旋转 rotate
旋转变换
rotate(θ),相当于对其应用如下变换矩阵:即等价于矩阵变换函数
matrix(cosθ, sinθ, -sinθ, cosθ, 0, 0)。倾斜 skew
倾斜变换
skew(α, β),相当于对其应用如下变换矩阵:即等价于使用矩阵变换函数
matrix(1, tanβ, tanα, 1, 0, 0)。缩放 scale
缩放变换
scale(scaleX, scaleY),相当于对其应用如下变换矩阵:即等价于使用矩阵变换函数
matrix(scaleX, 0, 0, scaleY, 0, 0)。3D变换 matrix3d()
在 3D变换中,矩阵变换函数
matrix3d()接受 16 个值,语法形式如下:在 齐次坐标 下相当于变换矩阵:
3D 矩阵坐标变换

在 3D变换中,变换总共有以下几种操作:
transform: translate3d(X, Y, Z)transform: rotate3d(X, Y, Z, θ)transform: scale3d(scaleX, scaleY, scaleZ)这些对应的变换矩阵分别如下:
平移 translate3d
平移变换
translate3d(X, Y, Z),相当于对其应用如下变换矩阵:即等价于使用矩阵变换函数
matrix3d(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, X, Y, Z, 1)。旋转 rotate3d
旋转变换
rotate3d(x, y, z, α),相当于对其应用如下变换矩阵:缩放 scale3d
缩放变换
scale3d(scaleX, scaleY, scaleZ),相当于对其应用如下变换矩阵:即等价于使用矩阵变换函数
matrix3d(scaleX, 0, 0, 0, 0, scaleY, 0, 0, 0, 0, scaleZ, 0, 0, 0, 0, 1)。Other Resources
理解矩阵乘法
matrix()
matrix3d()
Transform Functions
笛卡尔坐标系
3D数学基础-向量运算基础和矩阵变换
The text was updated successfully, but these errors were encountered: