Prima di passare agli appunti del corso un chiarimento che ho elaborato a partire da wikipedia-en.
Spesso risulta utile considerare lo spettro di una porzione finita del segnale, risulta quindi comodo applicare una funzione finestra al segnale stesso.
Un esempio di funzione finestra:
RectangularWindow(n) : 1 if n in [0,L-1], 0 otherwise
La finestra ci permette di considerare il segnale solo nel range che desideriamo.
Prendiamo come esempio la funzione cos(ωt). Per definizione il suo spettro
dovrebbe essere 0 per frequenze diverse da ω. Se andiamo ad applicare una
finestra rettangolare lo spettro della sinusoide non appare più come un impulso
unitario in ω, ma comprende delle frequenze con ampiezza diversa da 0, e in
particolare, le ampiezze saranno più accentuate vicino a ω, e comunque spalmate
in tutto lo spettro. Questo effetto viene detto leakage spettrale.
Se le forme d'onda sotto analisi comprendono due sinusoidi, il leakage prodotto dall'applicazione delle finestre può interferire con l'abilità di distinguere le 2 sinusoidi accuratamente. Infatti se le loro frequenze e ampiezze son diverse, la sinusoide con ampiezza minore potrebbe essere indistinguibile a causa del leakage prodotto da quella con ampiezza maggiore. Inoltre, se le sinuosidi hanno ampiezza simile ma frequenze molto simili, il loro effetto leakage le renderà indistinguibili.
La finestra rettangolare ha una risoluzione spettrale eccellente per sinusoidi di forza comparabile, ma è una scelta povera per sinusoidi a diverse ampiezze.
Spectral Analysis on Wikipedia
Se il segnale da osservare è analogico, lo filtreremo con un low-pass e campioneremo
con frequenza di campionamento f > 2B (con B larghezza di banda).
Il limite che ci pone il campionamento è l'impossibilità di distinguere
frequenze con separazione inferiore a 1 / LT. (con L numero di campioni).
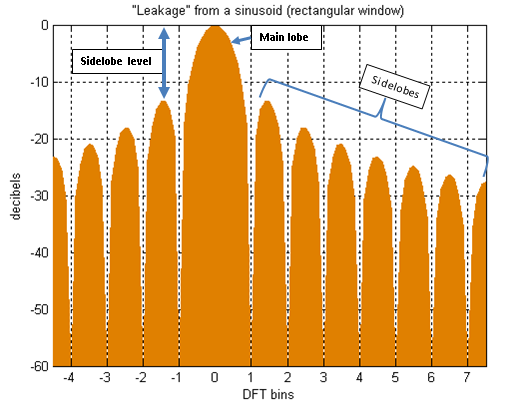
Campionando una sinuoside all'interno di una finestra rettangolare otteniamo uno spettro con un lobo primario in prossimità della frequenza della sinusoide, e dei lobi secondari intorno a tutto lo spettro. Si parla di leakage.
All'aumentare di L, ovvero aumentando il range [a, b] della finestra di
osservazione, abbiamo che il lobo principale viene ristretto in lunghezza, ma i
lobi secondari non si attenuano.
Per ridurre i lobi secondari, che influiscono in male sulla risoluzione spettrale, possiamo adottare delle funzioni finestre alternative. Nel nostro corso vanno molto di moda le seguenti:
Hamming(n) = 0.54 - 0.46 cos (2πn/(L-1)) if n in [0, L-1],
0 otherwise
Hanning(n) = 0.5 - 0.5 cos (2πn/(L-1)) if n in [0, L-1],
0 otherwise
Utilizzando queste finestre gli spettri hanno dei lobi secondari molto più attenuati rispetto agli spettri ottenuto in seguito ad applicazione della finestra rettangolare.
L'attenuazione dei lobi secondari si ha a spese dell'allargamento del lobo
principale e quindi a spese di una perdita di risoluzione, che viene compensata
se si aumenta L.
Lo spettro di solito viene valutato tramite FFT su una sequenza di durata L, che coincide con la DTFT campionata su L punti equidistanziati nell'intervallo [0, 2π]
Ricordiamo che lo spettro della DTFT (e quindi anche della DFT) è periodico di periodo 2π e che se la sequenza è reale allora il suo spettro è a simmetria coniugata (di conseguenza le frequenze nell'intervallo [0,π] hanno la stessa parte reale e lo stesso modulo di quelle nell'intervallo [2π, π], ma hanno parte immaginaria con segno opposto e quindi fasi opposte).
# FFT Tramite octave, il primo elemento dell'array non sembra avere senso fisico
# ma gli altri hanno tutti simmetria coniugata
octave:5> a = fft([1,2,3,4,5,6,7,8])
a =
36.0000 + 0.0000i
-4.0000 + 9.6569i
-4.0000 + 4.0000i
-4.0000 + 1.6569i
-4.0000 + 0.0000i
-4.0000 - 1.6569i
-4.0000 - 4.0000i
-4.0000 - 9.6569i
# moduli
octave:6> abs(a)
ans =
36.0000 10.4525 5.6569 4.3296 4.0000 4.3296 5.6569 10.4525
# fasi
octave:7> arg(a)
ans =
0.00000 1.96350 2.35619 2.74889 3.14159 -2.74889 -2.35619 -1.96350