You are given an n x n integer matrix grid.
Generate an integer matrix maxLocal of size (n - 2) x (n - 2) such that:
- maxLocal[i][j] is equal to the largest value of the 3 x 3 matrix in grid centered around row i + 1 and column j + 1.
In other words, we want to find the largest value in every contiguous 3 x 3 matrix in grid.
Return the generated matrix.
Example 1:
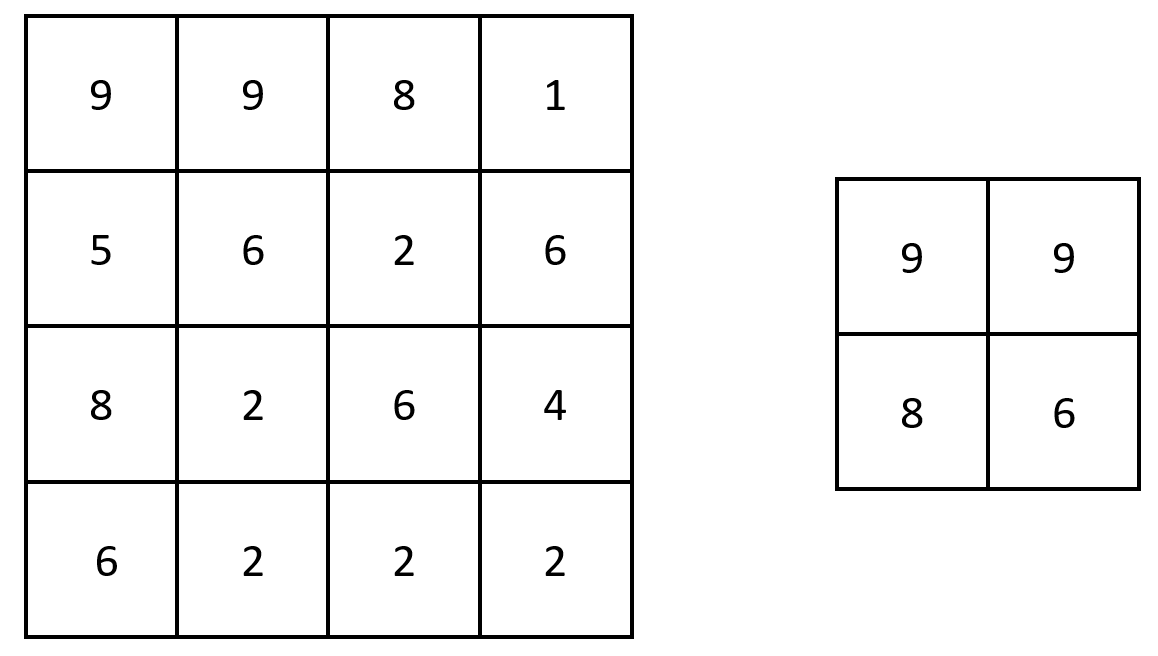
Input: grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
Output: [[9,9],[8,6]]
Explanation: The diagram above shows the original matrix and the generated matrix.
Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.
Example 2:
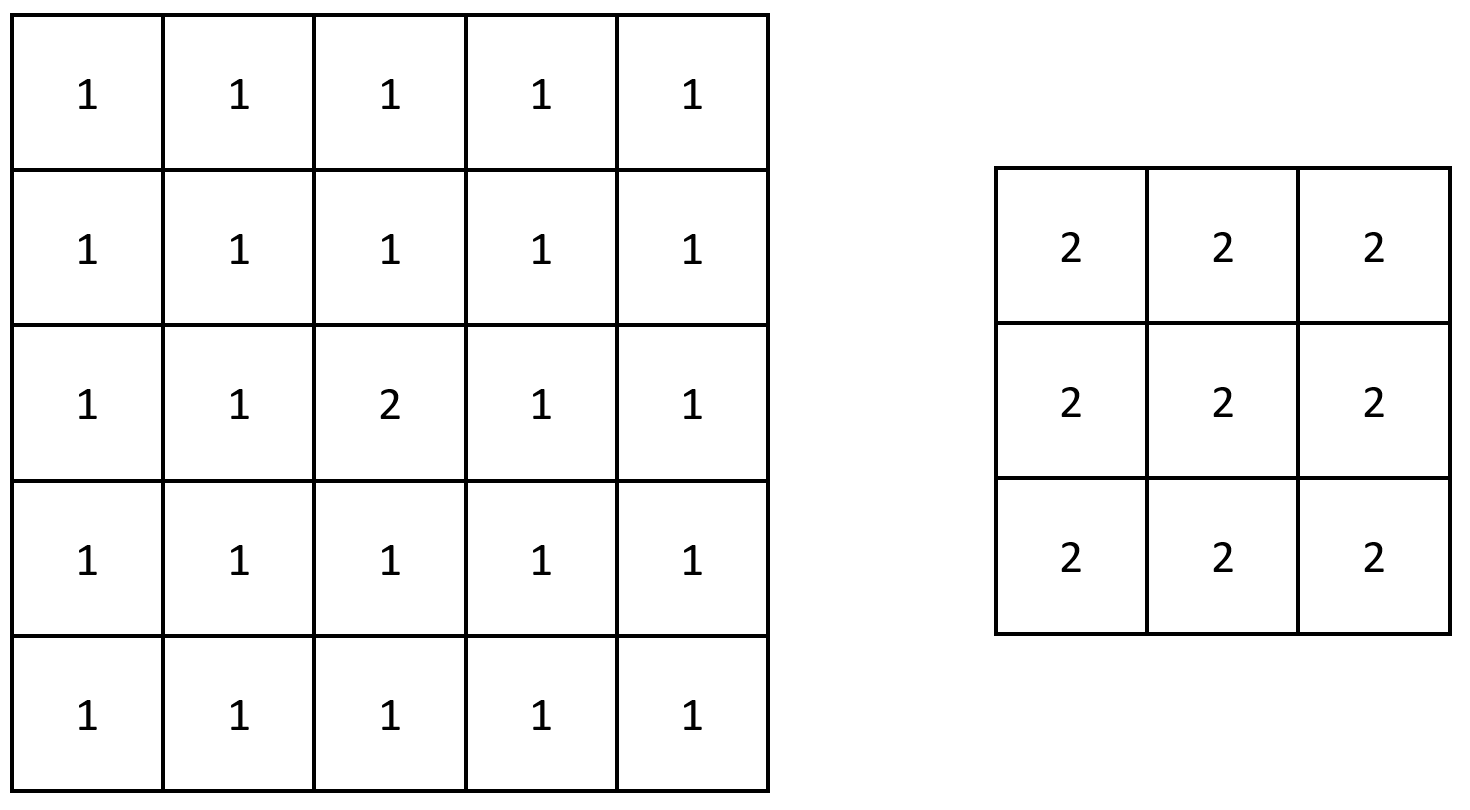
Input: grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
Output: [[2,2,2],[2,2,2],[2,2,2]]
Explanation: Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.
Solution
class Solution:
def largestLocal(self, grid: List[List[int]]) -> List[List[int]]:
n = len(grid)
matrix = [[1] * (n - 2) for i in range(n - 2)]
for i in range(0, n-2):
for j in range(0, n-2):
maxx = 0
for row in range(i, i + 3):
for col in range(j, j + 3):
maxx = max(maxx, grid[row][col])
matrix[i][j] = maxx
return matrix