1582_special_positions_in_a_binary_matrix.md

Special Positions in a Binary Matrix

Given an m x n binary matrix mat, return the number of special positions in mat.

A position (i, j) is called special if mat[i][j] == 1 and all other elements in row i and column j are 0 (rows and columns are 0-indexed).

Example 1:

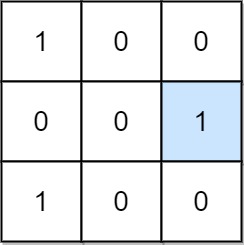
Input: mat = [[1,0,0],[0,0,1],[1,0,0]]
Output: 1
Explanation: (1, 2) is a special position because mat[1][2] == 1 and all other elements in row 1 and column 2 are 0.

Example 2:

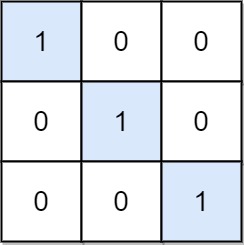
Input: mat = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3
Explanation: (0, 0), (1, 1) and (2, 2) are special positions.

Solution

class Solution:
    def numSpecial(self, mat: List[List[int]]) -> int:
        cnt = 0
        rows = len(mat)
        cols = len(mat[0])
        row_sum = list()
        col_sum = list()

        for r in mat:
            row_sum.append(sum(r))
        for c in zip(*mat):
            col_sum.append(sum(c))

        for r in range(rows):
            for c in range(cols):
                if mat[r][c] == 1 and row_sum[r] == 1 and col_sum[c] == 1:
                    cnt += 1
        return cnt