在引出对称加密之前,有必要先介绍一种位运算,XOR。XOR 的全称是 exclusive or,中文翻译是异或。
0 XOR 0 = 0
0 XOR 1 = 1
1 XOR 0 = 1
1 XOR 1 = 0XOR 可以看成是“两个数相同,异或为 0 ,不同则异或为 1”。
异或也叫半加运算,其运算法则相当于不带进位的二进制加法:二进制下用1表示真,0表示假,则异或的运算法则为:
0 ⊕ 0 = 0
1 ⊕ 0 = 1
0 ⊕ 1 = 1
1 ⊕ 1 = 0这些法则与加法是相同的,只是不带进位,所以异或常被认作不进位加法。由异或的这种特点,也就引出了它的一个常用特性,两个相同的数进行 XOR 运算的结果一定为 0。
对应的,我们也可以得到如下的运算法则:
1. a ⊕ a = 0
2. a ⊕ b = b ⊕ a 交换率
3. a ⊕ b ⊕ c = a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c 结合律
4. d = a ⊕ b ⊕ c 可以推出 a = d ⊕ b ⊕ c
5. a ⊕ b ⊕ a = b上述这几条法则推导过程就不赘述了,相信读者都能明白。
异或的结合律可以用来做简单的对称加密。
试想,如果把异或数设置成一个完全随机的二进制序列,那么被异或数和它进行一次异或运算以后,结果如同“密文”一样。如果窃听者不知道异或数是什么,很难短时间内解出原消息来。
a ⊕ b ⊕ b = a ⊕ (b ⊕ b) = a ⊕ 0 = a消息接收者拿到密文以后,把密文再和异或数进行一起异或运算,就能拿到原文了。这个性质就是异或的结合律。
只要通过暴力破解,对密钥空间进行遍历,密文总有一天一定能被破译。只不过看密钥空间有多大,需要花费的时间有多长。但是有一种加密方法却是被证明永远都无法被破解的,即便是暴力遍历了所有密钥空间,依旧无法被破解。
笔者第一次见到这个加密方法的时候,觉得非常神奇,还有这么强大的加密方法,那加密过程应该非常复杂,数学证明也应该非常完备吧。结果看到它的原理以后,发现并非如此。一次性密码本的加密方法非常简单,只用了上一章提到的 XOR 异或运算。
一次性密码本加密,举个例子,假设要加密的原文是 midnight。
密钥为一个随机的二进制流。一次性密码本加密的过程,是把明文和密钥进行一次异或计算。
一次性密码本的解密过程是把密文和密钥进行一次异或计算,得到原文明文。
看完这个加密解密过程,读者肯定质疑这种方式很容易被破解啊,64 位随机的二进制流暴力遍历它的密钥空间,一定能试出原文是什么。
那么现在就可以解开谜底了。确实用暴力破解能遍历所有密钥空间,假设有一个超级量子计算机可以一秒遍历完 2^64^ 这么大的密钥空间,但是依旧没法破译一次性密码本。它的“神奇”之处在于,你在不断尝试的过程中,会尝试出很多种情况,比如可能得到 abcdefg、aaaaa、plus、mine 这些原文,但是你无法判断此时你是否破译正确了。这也就是一次性密码本无法破译的原因,和密钥空间大小无关。
一次性密码本无法破译这一特性是由香农(C.E.Shannon)于 1949 年通过数学方法加以证明的。一次性密码本是无条件安全的(unconditionally secure),理论上是无法破译的(theoretically unbreakable)。
一次性密码本虽然这么强大,但是现实中没有人用一次性密码本进行加密。原因有一下几点:
在一次性密码本中,密钥和原文是一样长度的,试想如果有办法能把密文安全的送达到对方,那么是否可以用这种方法把明文送达到对方呢?所以这是一个矛盾的问题。
一次性密码本的密钥长度和原文一样长,密钥不能删除也不能丢弃。丢弃了密钥相当于丢弃了明文。所以“加密保护明文”的问题被转换成了“如何安全的保护和明文一样长度的密钥”的问题,实际上问题还是没有解决。
如果加密的原文很长,那么密钥也要相同长度,并且密钥每次还要不同,因为如果是相同的,密钥一旦泄露7以后,过去所有用这个密钥进行加密的原文全部都会被破译。
如果密钥每次都变化,那么密钥如何同步也是一个问题。密钥在传递过程中不能有任何错位,如果错位,从错位的那一位开始之后的每一位都无法解密。
一次性密码本想要真正的永远无法破解,就需要生成大量的真正的随机数,不能是计算机生成的伪随机数。
据说国家之间的热线电话用的就是一次性密码本,但是是如何避免上述 5 点缺点的呢?国家会派专门的特工,用人肉的方式进行押送密钥的任务,直接把密钥交到对方的手中。
可见一次性密码本虽然无法破译,但是想要用它进行加密,“成本”非常高。如此可见一次性密码本在日常使用中基本没有任何使用价值。不过一次性密码本的思路孕育了 流密码(stream cipher)。流密码使用的不是真正的随机比特序列,而是伪随机数生成器产生的二进制比特序列。流密码虽然不是无法破译的,但只要使用高性能的伪随机数生成器就能够构建出强度较高的密码系统。流密码在下面章节会详细分析。
DES (Data Encryption Standard) 是 1977 年美国联邦信息处理标准(FIPS)中所采用的一种对称密码(FIPS 46-3)。DES 一直以来被美国以及其他国家的政府和银行所使用。
1997 年 DES Challenge I 比赛中用了 96 天破解了 DES 密钥,1998 年的 DES Challenge II-1 比赛中用了 41 天就破解了密钥。1998 年的 DES Challenge II-2 比赛中用了 56 个小时,1999 年的 DES Challenge III 比赛中只用了 22 小时 15 分钟。目前来说,DES 已经不再安全了。除了用来解密以前老的 DES 密文以外,不再使用 DES 进行加密了。
DES 是一种把 64 位明文加密成 64 位密文的对称加密算法。它的密钥长度为 64 比特,但是除去每 7 个二进制位会设置一个用于错误检测的位以外,实际上密钥为 56 比特。DES 会以 64 个二进制为一个分组进行加密。以分组为单位进行处理的密码算法成为分组密码,DES 为分组密码的一种。
DES 只能一次性加密 64 位明文,如果明文超过了 64 位,就要进行分组加密。反复迭代,迭代的方式成为模式。关于模式更加具体的讨论见下一章节。
DES 加密的基本结构是 Feistel 网络、Feistel 结构、Feistel 密码,这个结构不仅仅用在 DES 中,还用在其他的加密算法中。
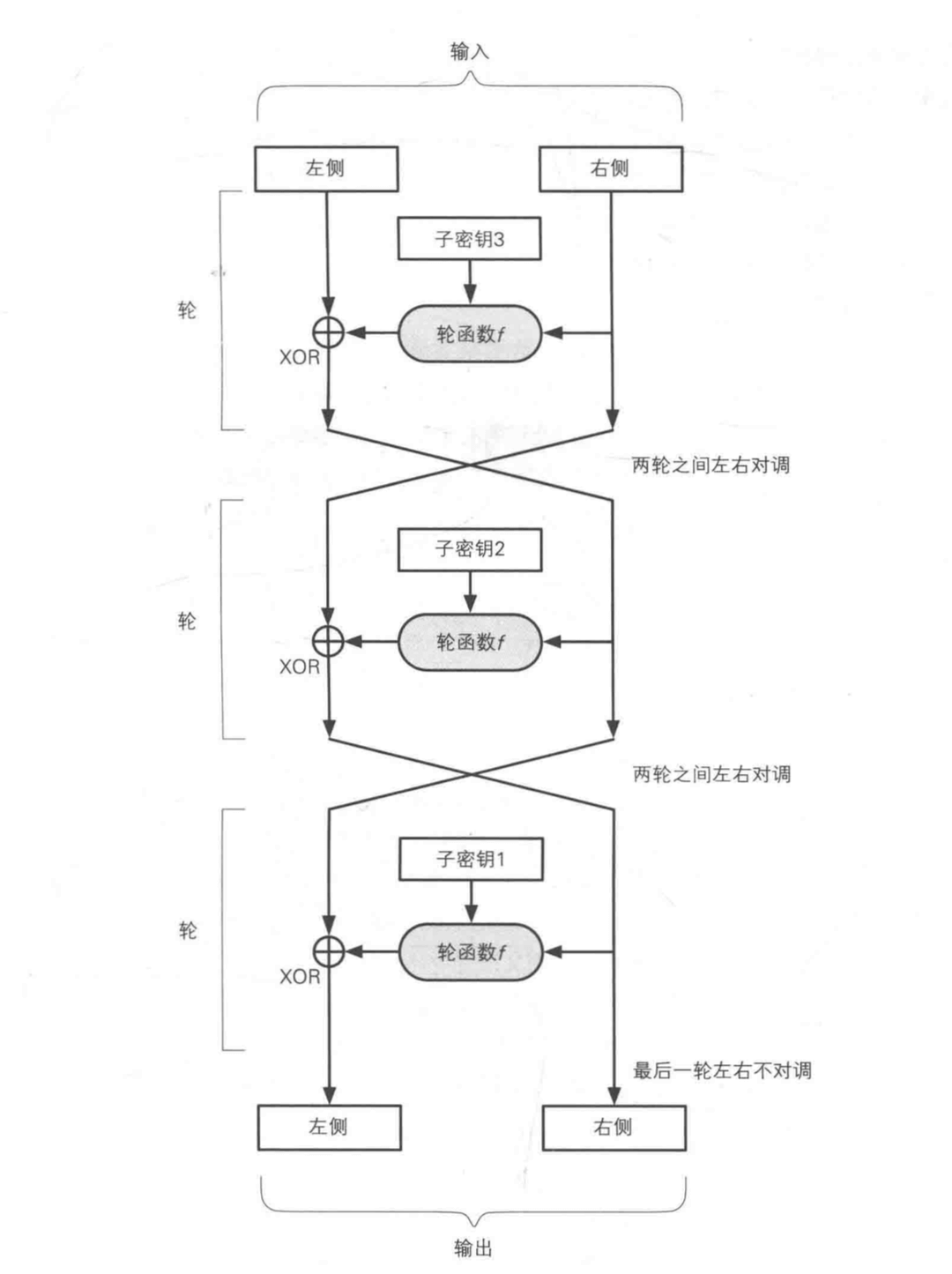
在 Feistel 网络中,加密的各个步骤称为轮(round),整个加密过程就是若干次轮的循环。DES 是一种 16 轮循环的 Feistel 网络。
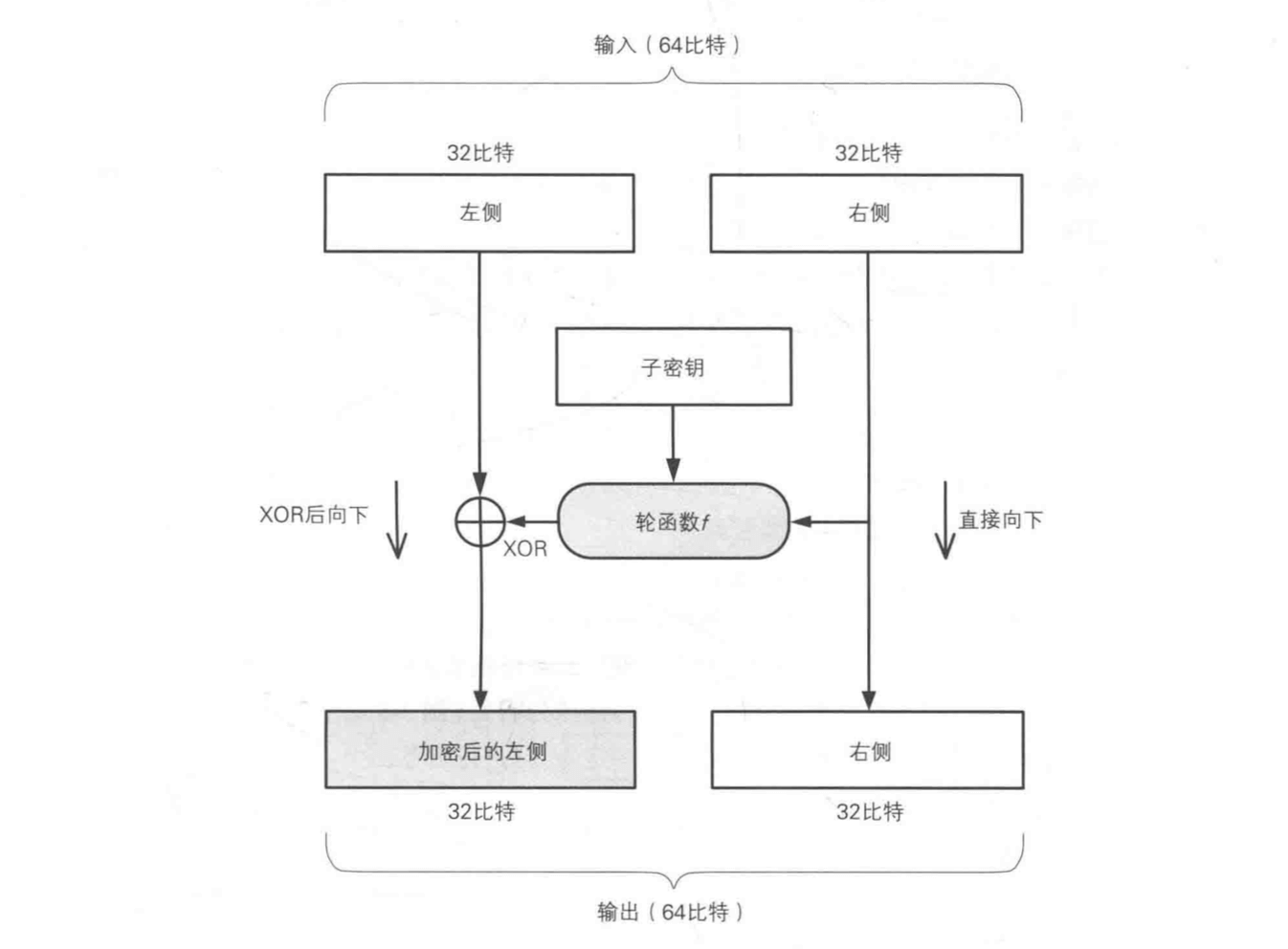
上图展示的是一次加密 64 位明文的过程。每次加密所用的密钥都不同,由于它只在本轮使用,是一个局部密钥,所以也被称为子密钥。
每轮的操作步骤如下:
- 将输入的 64 位分为左右两个 32 位。
- 将输入右侧的 32 位直接向下落到输出的右侧 32 位。
- 将输入右侧作为轮函数的入参输入。
- 轮函数根据输入右侧的 32 位和 子密钥两个入参,生成一串看上去随机的比特序列输出。
- 将轮函数的输出和输入左侧 32 位进行异或运算,结果向下落到输出的左侧 32 位。
这样经过一轮以后,只加密了输入的一半的数据,上例中右侧就没有被加密。我们可以用另外一个子密钥加密右侧的数据。
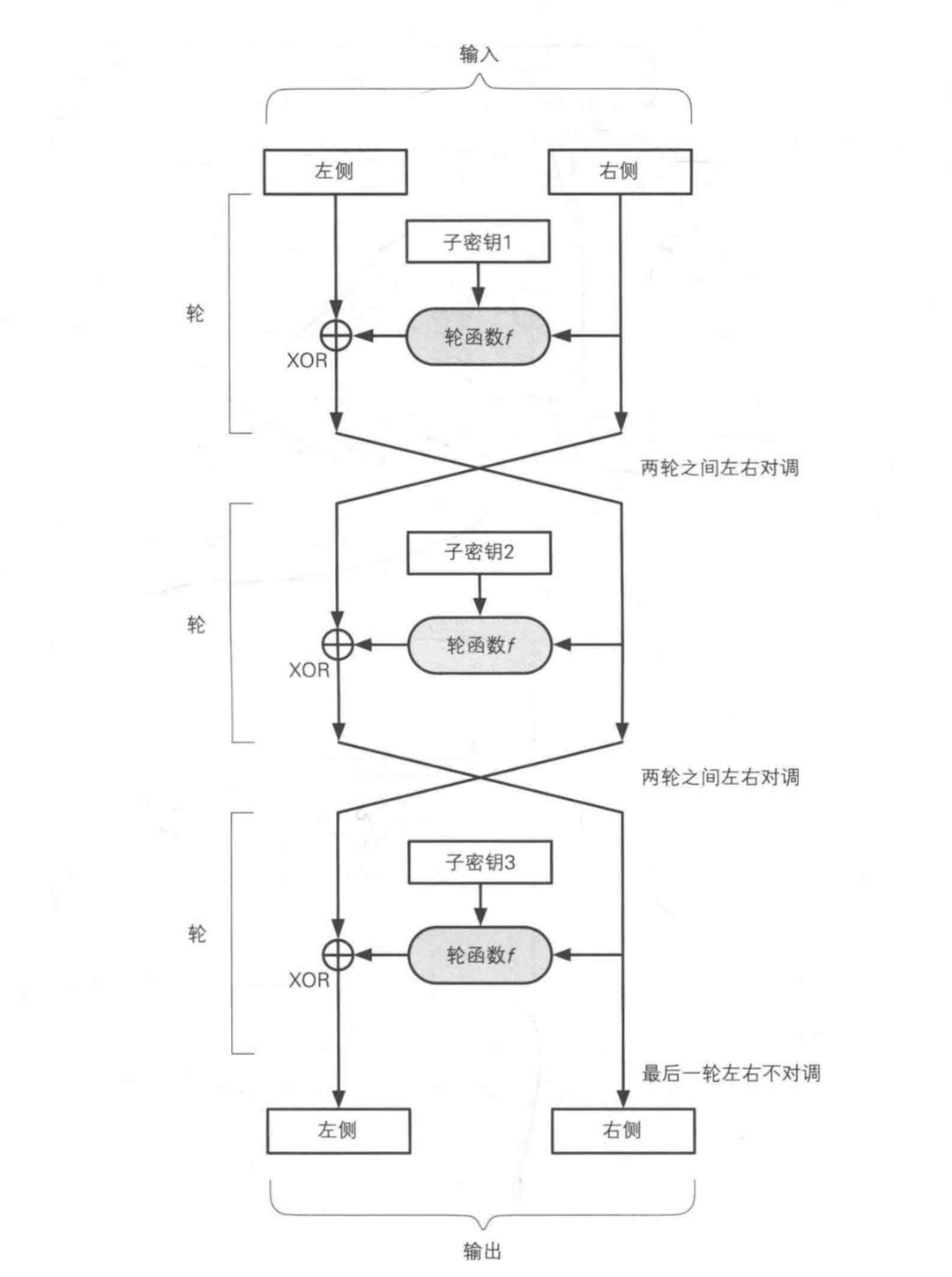
上图是一个 3 轮的 Feistel 网络。3 轮网络有 3 个子密钥和 3 个轮函数,中间有 2 次左右对调的过程。注意:n 轮 Feistel 网络只交换 n-1 次,最后一次不用交换。
DES 的解密过程和加密过程是相反的。解密也是 64 位分组解密。解密密钥实质也是 56 位。
再来聊聊 Feistel 网络的解密过程。
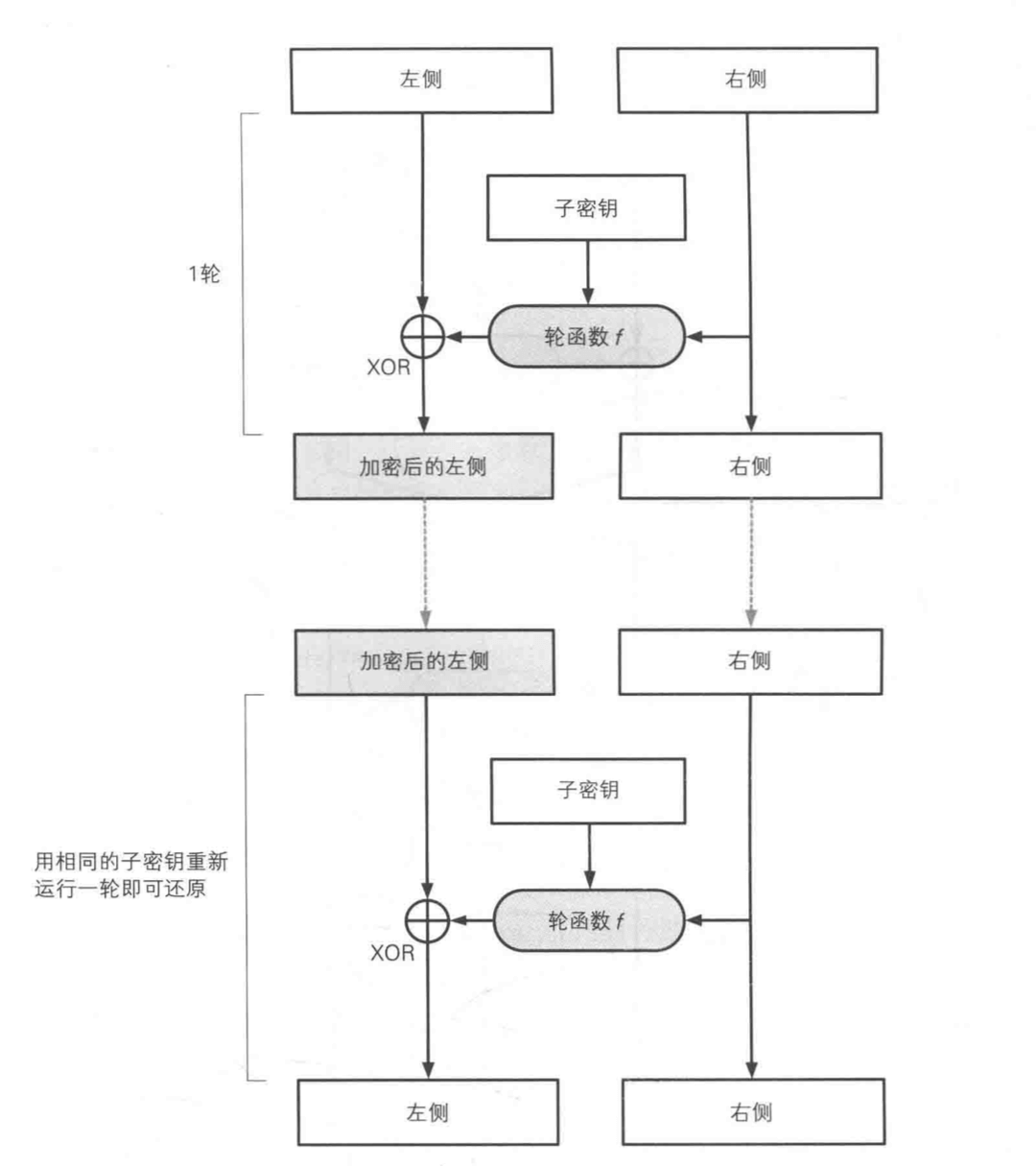
由于 XOR 具有交换律的特性,只要再次做一次异或运算,就能还原明文。
从上面这个图中,可以看出 Feistel 网络的加密和解密步骤完全相同。
同样也以 3 轮 Feistel 网络的解密过程来举例。
解密步骤也和加密步骤完全相同的,只不过子密钥的顺序是逆序的。因为要和之前加密的顺序配合在一起。假设是 n 轮网络,子密钥 1 - n,要想还原成明文,异或的顺序要逆序反过来,这样才能利用 a ⊕ a = 0,异或的结合律,还原明文。
Feistel 网络的特点
- 加密的时候无论使用任何函数作为轮函数都可以正确的解密,无须担心无法解密。就算轮函数输出的结果无法逆向计算出输入的值也无须担心。Feistel 网络把加密算法中核心的加密本质封装成了这个轮函数,设计算法的人把所有的心思放在把轮函数设计的尽量负责即可。
- 加密和解密可以用完全相同的结构来实现。虽然每一轮只加密了一半的明文,放弃了加密效率,但是获得了可以用相同结构来实现,对于加密硬件设备设计也变得更加容易。
由于 Feistel 网络的这些优点,所以很多分组密码选择了它。比如 AES 候选算法中的 MARS、RC6、Twofish。不过最终 AES 定下的 Rijndael 算法并没有选择它,而是选择的 SPN 网络。
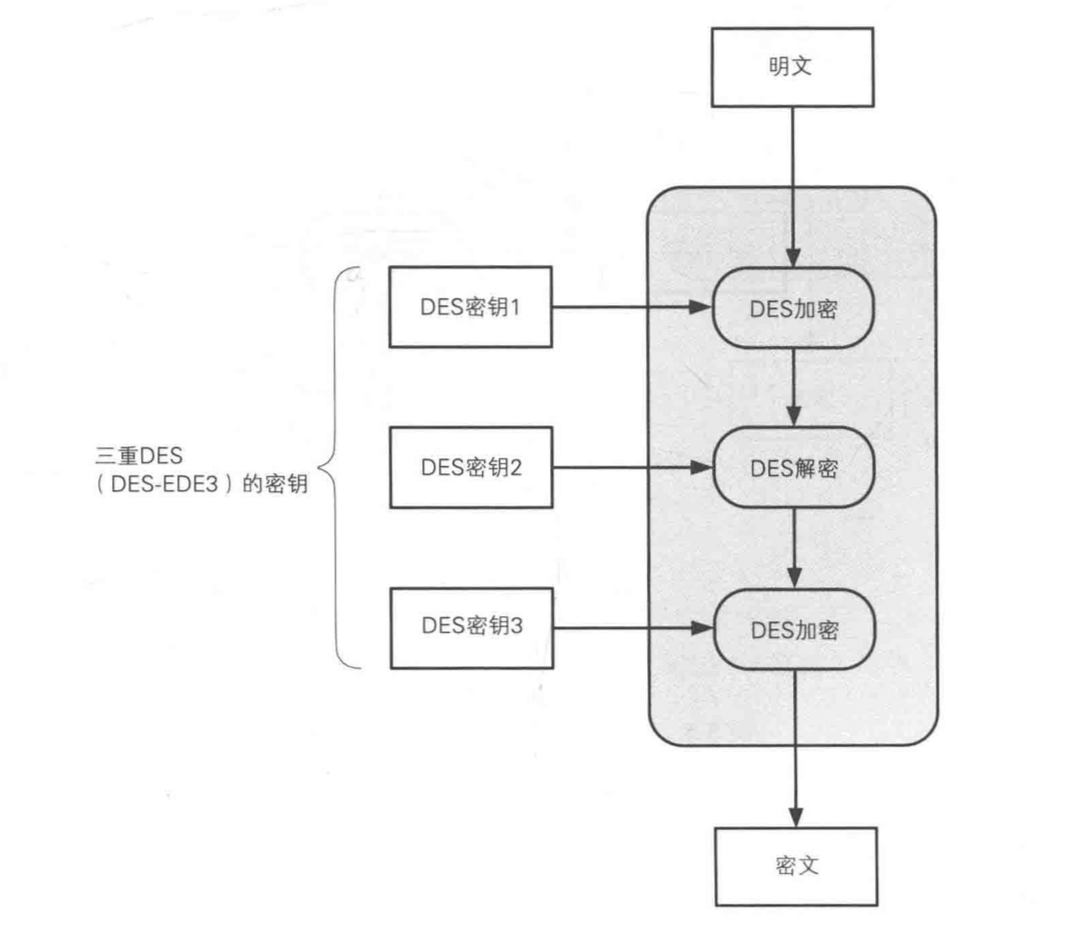
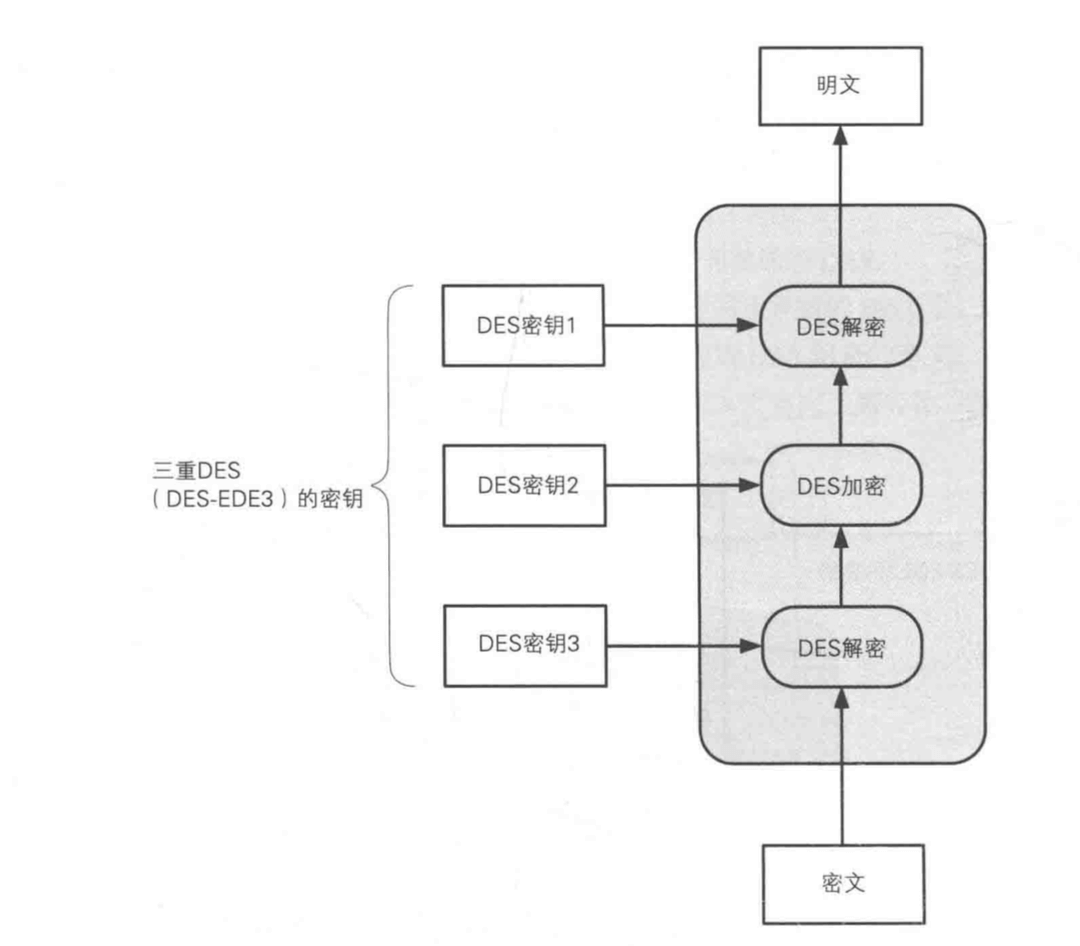
三重 DES (triple-DES) 是为了增加 DES 强度,所以将 DES 重复 3 次得到的一种算法。也称为 TDEA (Triple Data Encryption Algorithm),通常缩写为 3DES。
3DES 加密就是进行 3 次 DES 加密。DES 密钥长度为 56 位,所以 3DES 密钥长度为 56 * 3 = 168 位。
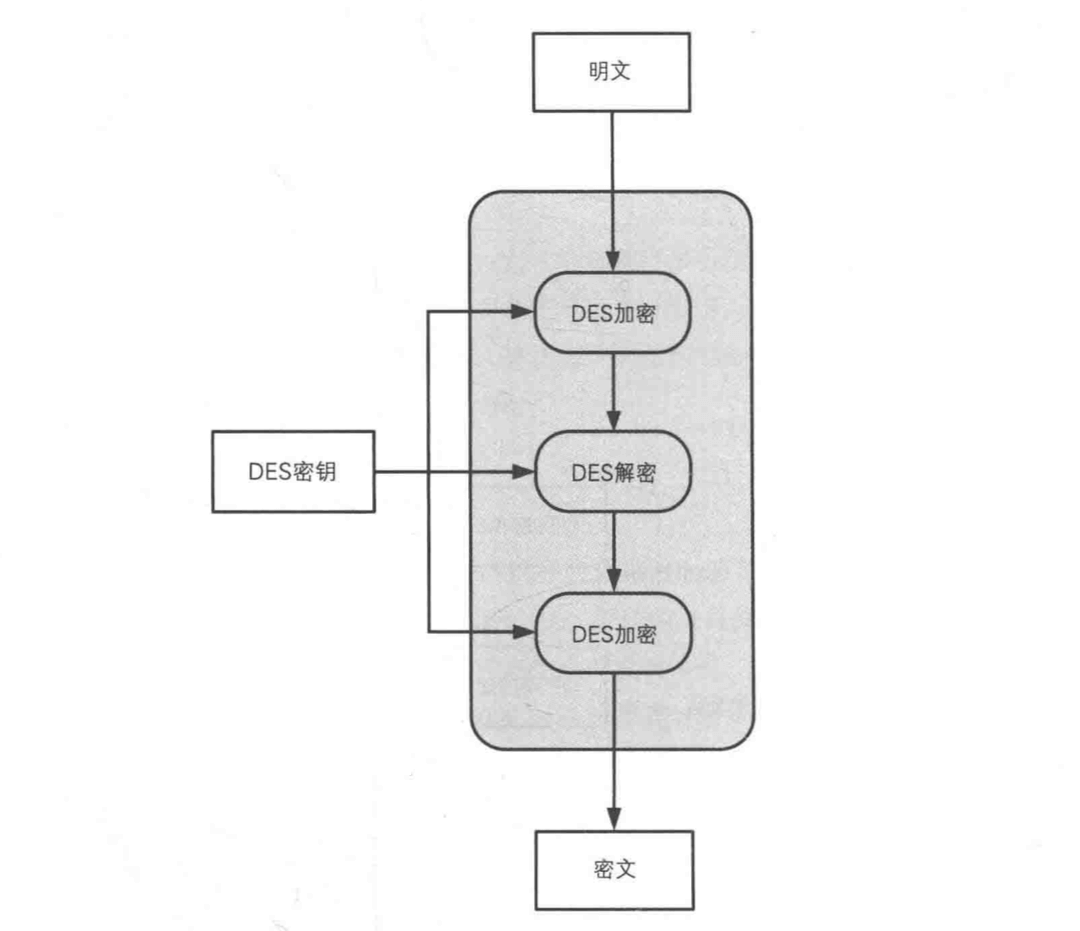
不过 3DES 有一个“奇怪”的地方,并不是用 DES 加密 3 次,而是加密-解密-加密,中间有一次解密的过程。IBM 公司之所以这么设计,目的是为了让三重 DES 能兼容普通的 DES。如果三重加密中密钥都完全相同,那么就退化成了普通的 DES 了。(加密一次解密一次就抵消了)所以也就具备了向下兼容性。
- 如果 3 次都用相同的密钥,则退化成了 DES。
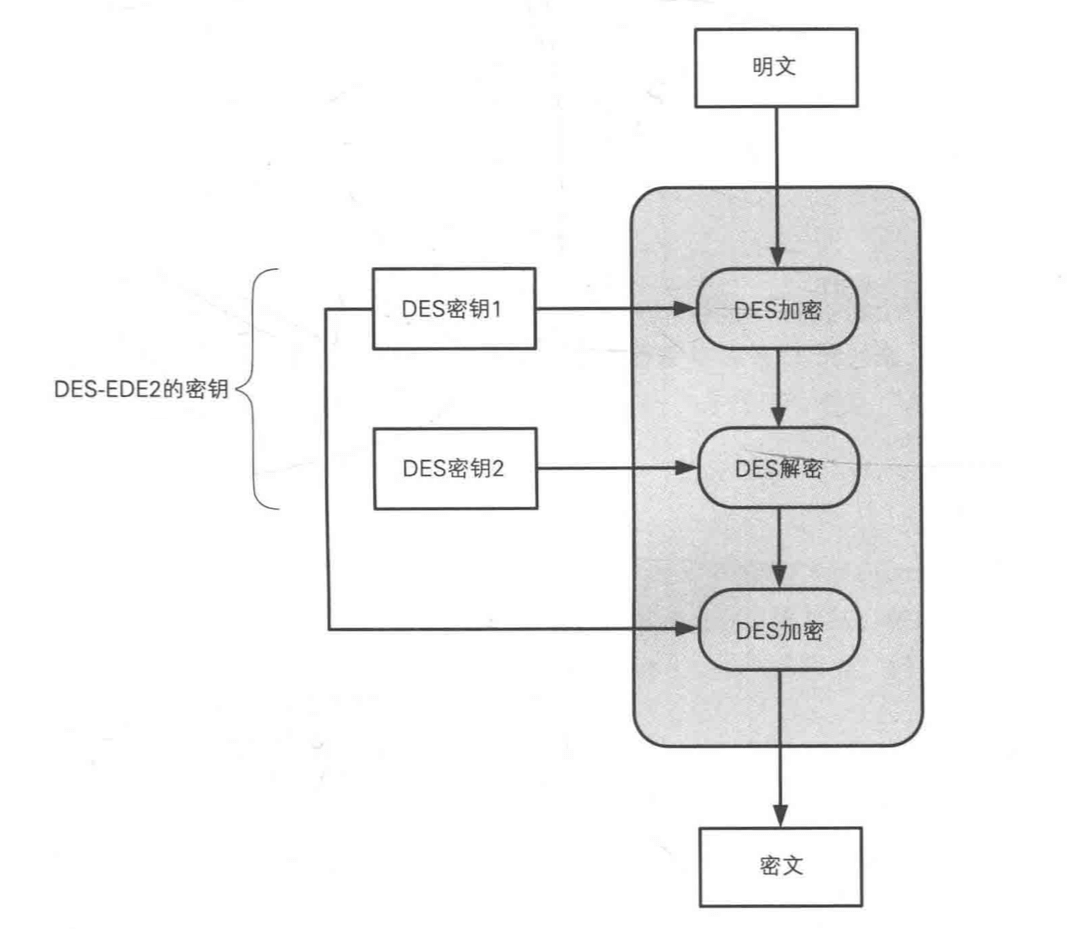
- 如果第一次和第三次用相同的密钥,第二次用不同的密钥,这种三重 DES 称为 DES-EDE2 。EDE 是加密(Encryption) -> 解密(Decryption) -> 加密(Encryption) 的缩写。
- 如果 3 次都用不同的密钥,则称 DES-EDE3。
3DES 解密的过程和加密的过程正好相反,按照密钥的逆序解密。
3DES 由于处理速度不高,除了兼容之前的 DES 以外,目前基本不再使用它了。
AES (Advanced Encrytion Standard) 是取代前任标准 DES 而成为新标准的一种对称密码算法。在全世界的范围内征集 AES 加密算法,最终于 2000 年从候选中选出了 Rijndael 算法,确定它为新的 AES。
1997 年开始征集 AES,1998 年满足条件并最终进入评审的有 15 个算法:CAST-256、Crypton、DEAL、DFC、E2、Frog、HPC、LOK197、Magenta、MARS、RC6、Rijndael、SAFER+、Serpent、Twofish。2000 年 10 月 2 日,Rijndael 并定位 AES 标准。AES 可以免费的使用。
Rijndael 的分组长度和密钥长度可以分别以 32 位比特为单位在 128 比特到 256 比特的范围内进行选择。不过在 AES 的规范中,分组长度被固定在 128 比特,密钥长度只有 128、192 和 256 比特三种。
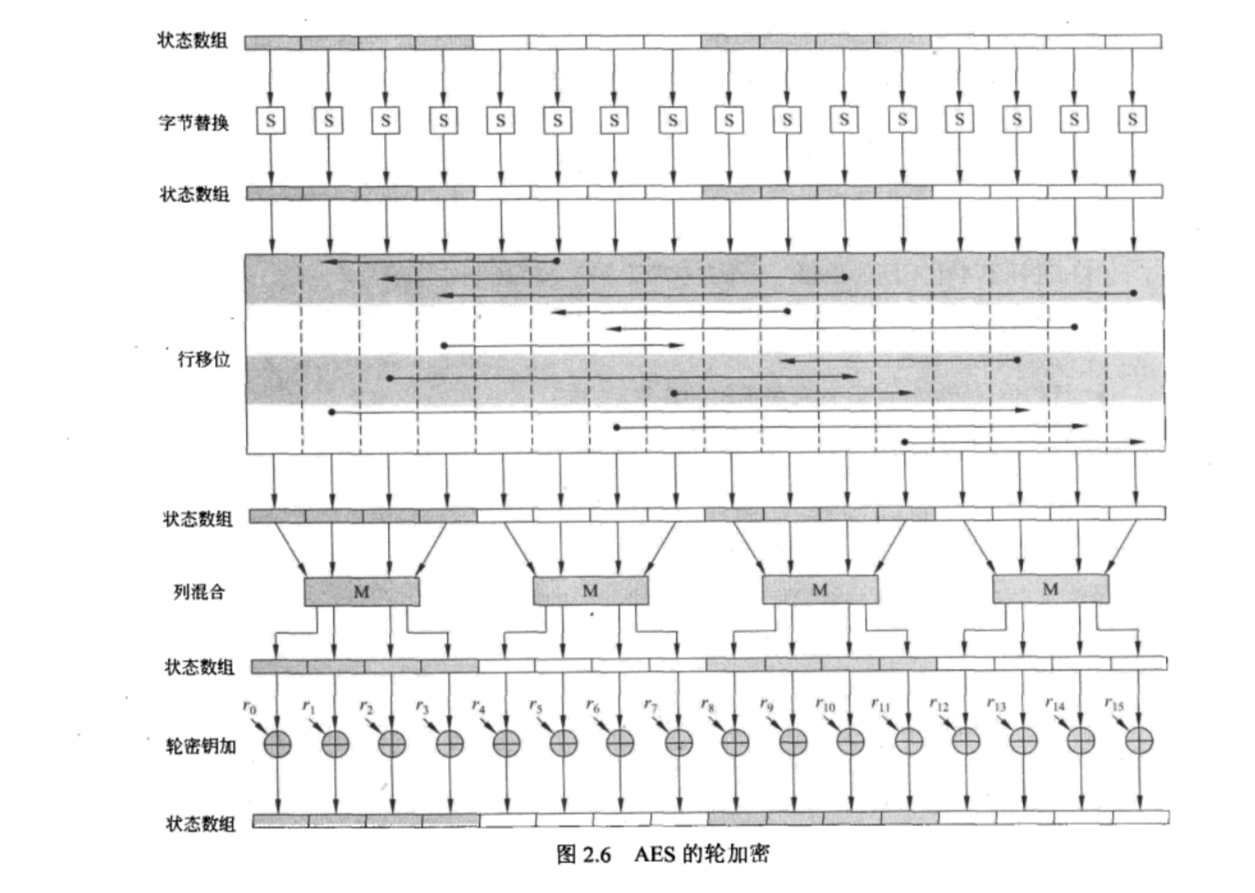
AES 的加密也是由多个轮组成的,分为 4 轮,SubBytes、ShiftRows、MixColumns、AddRoundKey 这 4 步,即 SPN 网络。
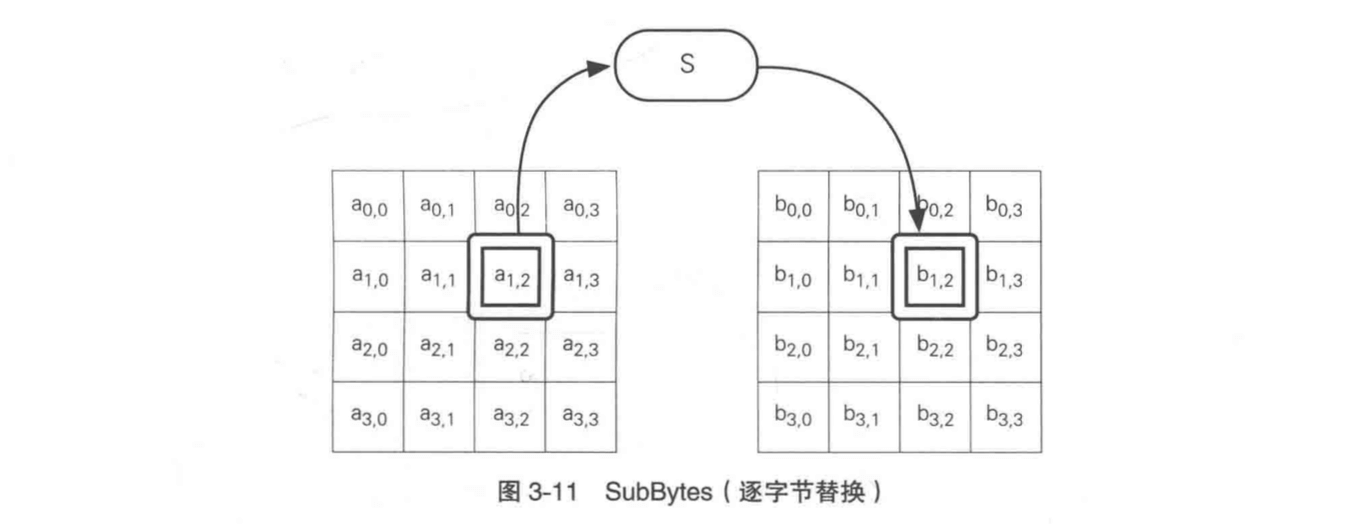
Rijndael 的输入分组默认为 128 比特,也就是 16 字节。第一步需要对每个字节进行 SubBytes 处理。以每个字节的值(0-255之间的任意值)为索引,从一张拥有 256 个值的替换表 S-Box 中查找出对应的值进行处理。
经过 SubBytes 变换以后,左边 16 个字节(128 个比特)都变换成右边的 16 个字节。
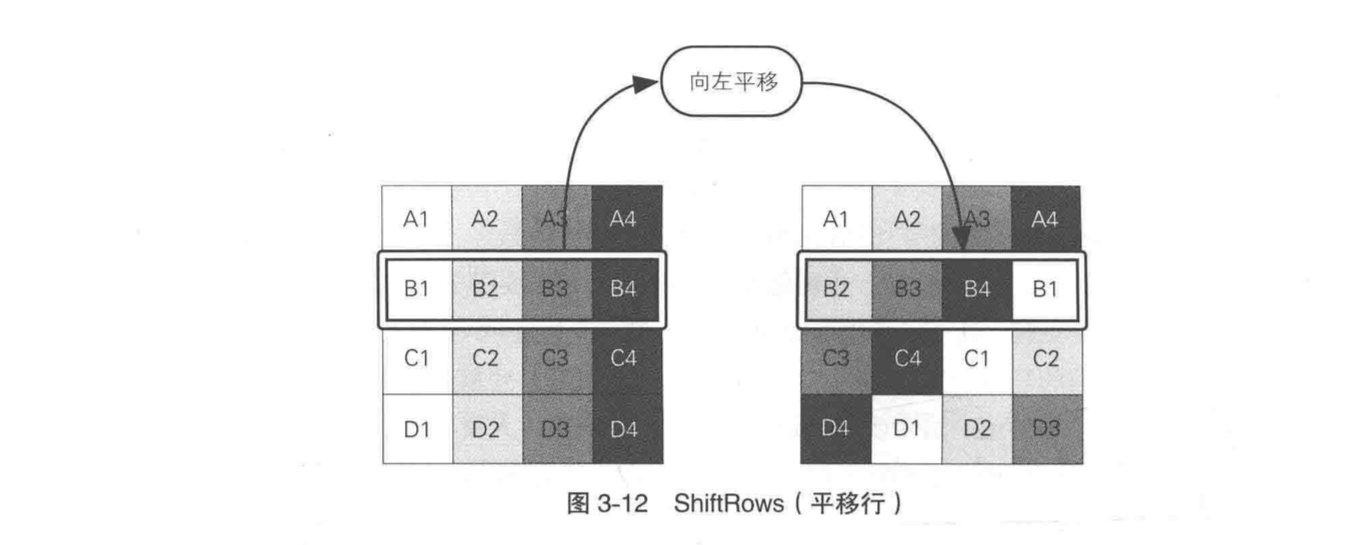
这一步以 4 字节为单位的行 row 进行左移操作,且每一行平移的字节数不同。
移动以后,每一行都“错位”了。
这一步以 4 字节为单位的列 column 进行矩阵运算。
经过这一步变换以后,每一列和之前的列都不同了。
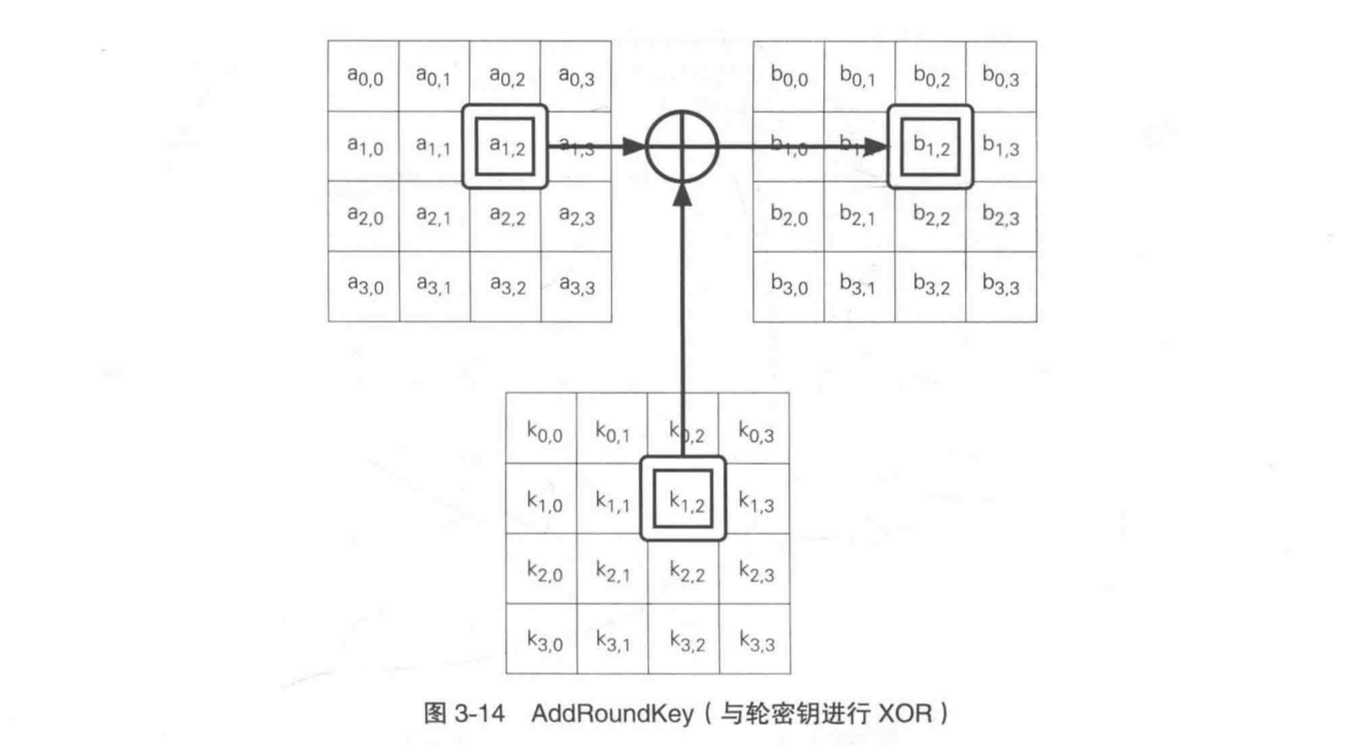
将上一步的输出与轮密钥进行 XOR,即进行 AddRoundKey 处理。
如上图,左边 16 字节每个字节一次与轮密钥对应位置上的字节进行异或运算,计算完成以后得到最终的密文。
到这里为止,是一轮 Rijndael 结束。
完成的一轮解密如下图:
一般整个算法要进行 10-14 轮计算。
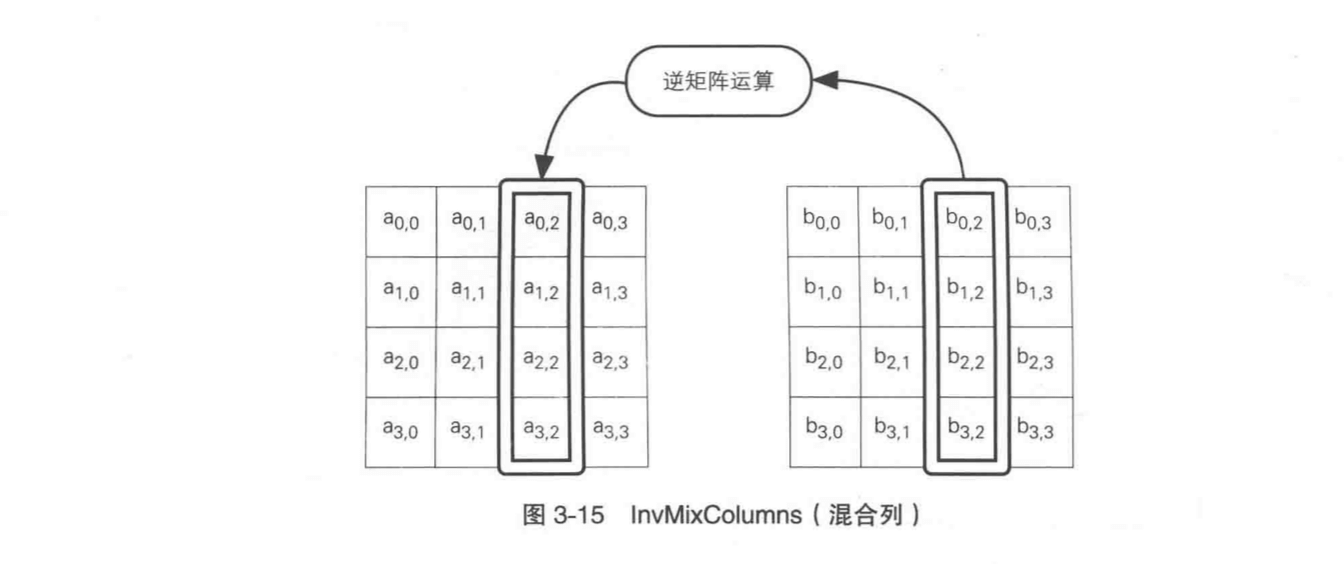
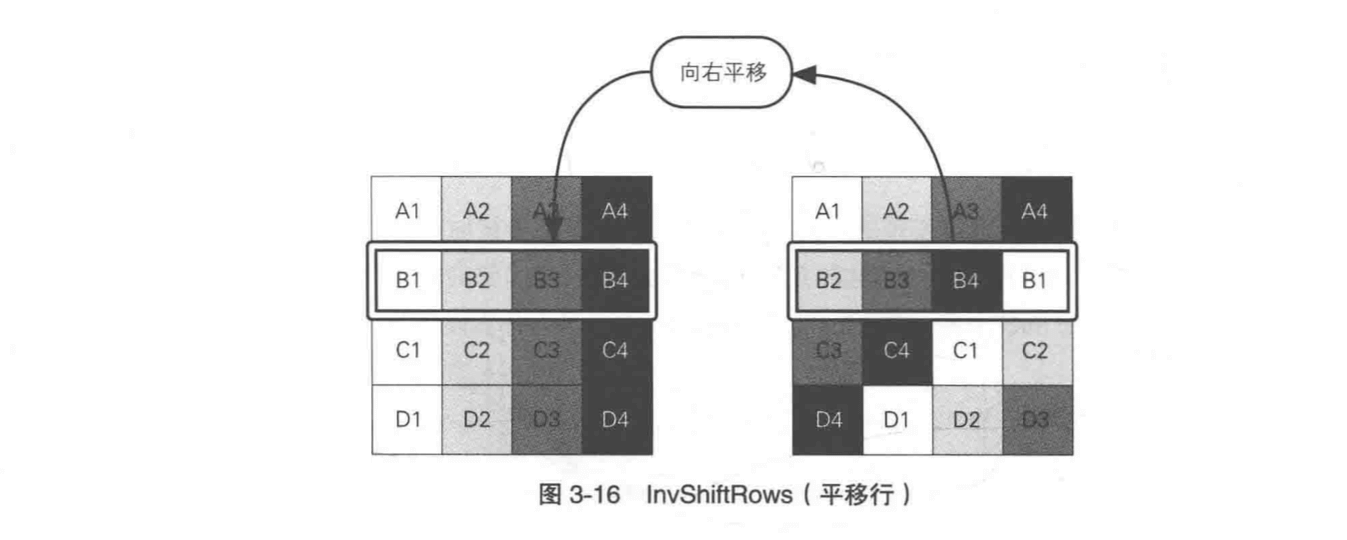
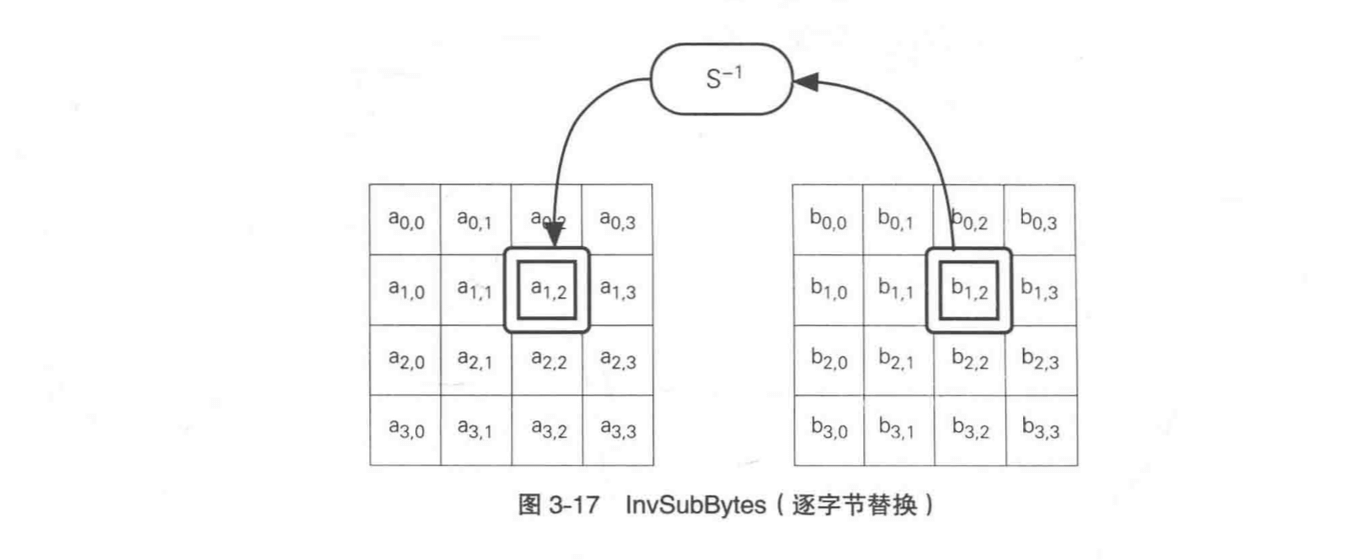
Rijndael 的解密过程为加密的逆过程。
在 Rijndael 加密过程中,每一轮处理的顺序为:
SubBytes -> ShiftRows -> MixColumns -> AddRoundKey
在 Rijndael 解密过程中,每一轮处理的顺序为:
AddRoundKey -> InvMixColumns -> InvShiftRows -> InvSubBytes
解密过程中除了第一步和加密完全一样,其他三步都为加密的逆过程。
SPN 网络和 Feistel 网络相比,加密效率更高,因为 SPN 一轮会加密所有位。所以加密所需轮数会更少。
还有一个优势在于加密用的 4 步可以并行运算。
目前还没有针对 AES 有效的攻击破译方式。
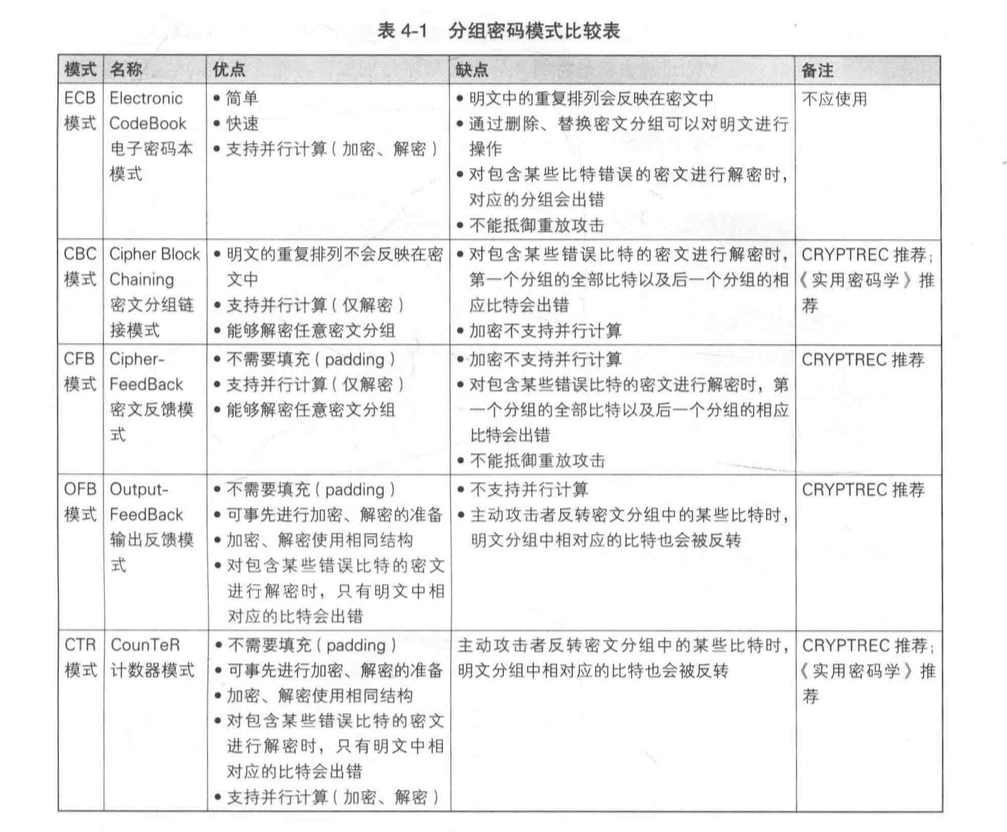
由于 DES 和 AES 一次加密都只能加密固定长度的明文,如果需要加密任意长度的明文,就需要对分组密码进行迭代,而分组密码的迭代方式就称为分组密码的“模式”。
分组密码有很多模式,如果模式选择的不恰当就无法充分保障机密性。
分组密码(block cipher) 是每次只能处理特定长度的一块数据的一类密码算法,这里的“一块”被称为分组。一个分组的比特数称为分组长度。例如 DES 和 3DES 的分组长度都是 64 位。AES 分组长度为 128 位。分组密码处理完一个分组以后就结束,不需要记录额外的状态。
流密码(stream cipher) 是对数据流进行连续处理的一类密码算法。流密码中一般以 1 比特、8比特、32比特等单位进行加密和解密。例如一次性密码本就属于流密码。流密码处理完一串数据以后,还需要保持内部的状态。
| 流密码算法 | 密钥长度 | 说明 |
|---|---|---|
| 一次性密码本 | 和原文相同长度 | 永远无法破译 |
| RC4 | 可变密钥长度,建议长度 2048 比特 | 目前已经被证明不再安全 |
| ChaCha | 可变密钥长度,建议长度 256 比特 | 一种新型的流密码算法 |
以 RC4 流密码算法为例,关键就在于算法内部生成了一个伪随机的密钥流(keystream),密钥流的特点如下:
- 密钥流的长度和密钥长度是一样的
- 密钥流是一个伪随机数,是不可预测的
- 生成伪随机数都需要一个种子(seed),种子就是 RC4 算法的密钥,基于同样一个密钥(或者称为种子),加密者和解密者能够获取相同的密钥流。
有了密钥流,之后加密解密就很容易了,就是 XOR 运算。
流密码算法之所以称为流密码算法,就在于每次 XOR 运算的时候,是连续对数据流进行运算的一种算法,每次处理的数据流大小一般是一字节。流密码算法可以并行处理,运算速度非常快。但是目前 RC4 已经被证明是不安全的。建议使用块密码。
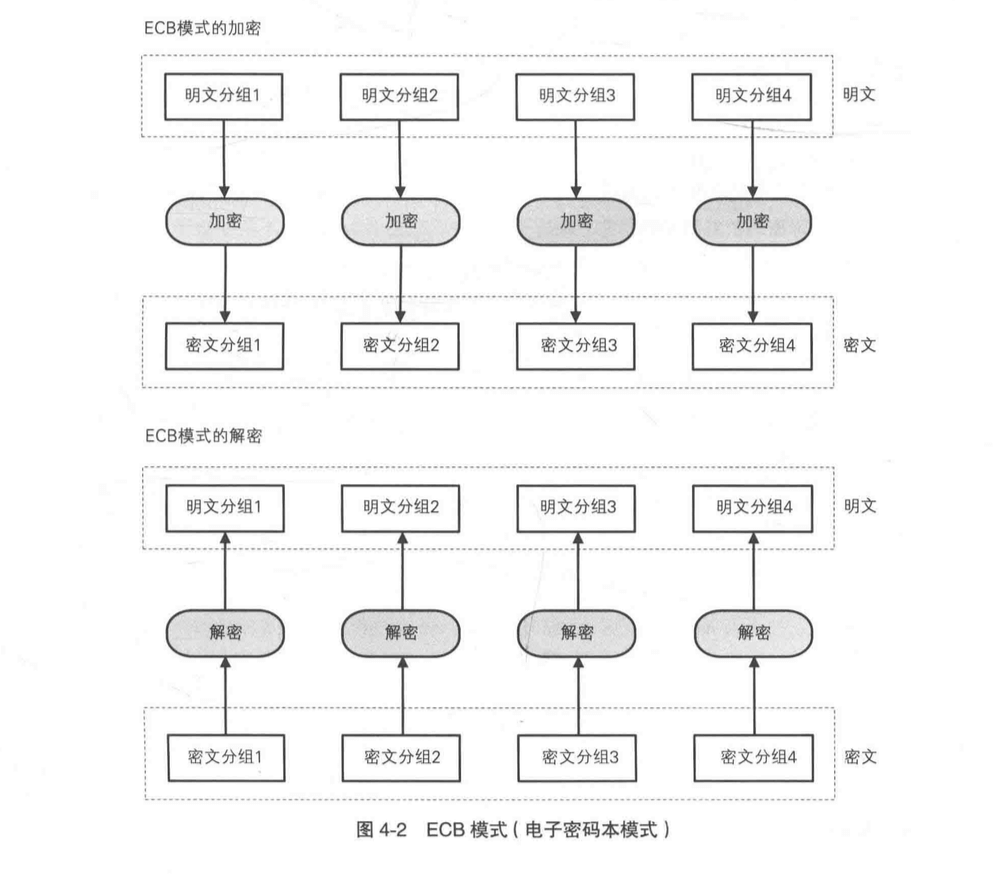
ECB 模式是分组模式里面最简单的,也是最没有安全性的。所以使用的人很少。
ECB 模式全称“Electronic CodeBook”模式,在 ECB 模式中,将明文分组加密之后的结果直接就是密文分组,中间不做任何的变换。
ECB 的加密和解密都非常直接。针对密文中存在多少种重复的组合就能以此推测明文,破译密码。所以 ECB 模式存在安全风险。
针对 ECB 的攻击有很多种,最简单的一种就是交换分组的位置。例如明文分组中 1,2 分组表示的明文消息是 付款方A 和 收钱方B,第 3 个分组中记录着转账金额。攻击者可以把 1,2 分组顺序逆序一下,这样消息的寓意完全颠倒。攻击成功。
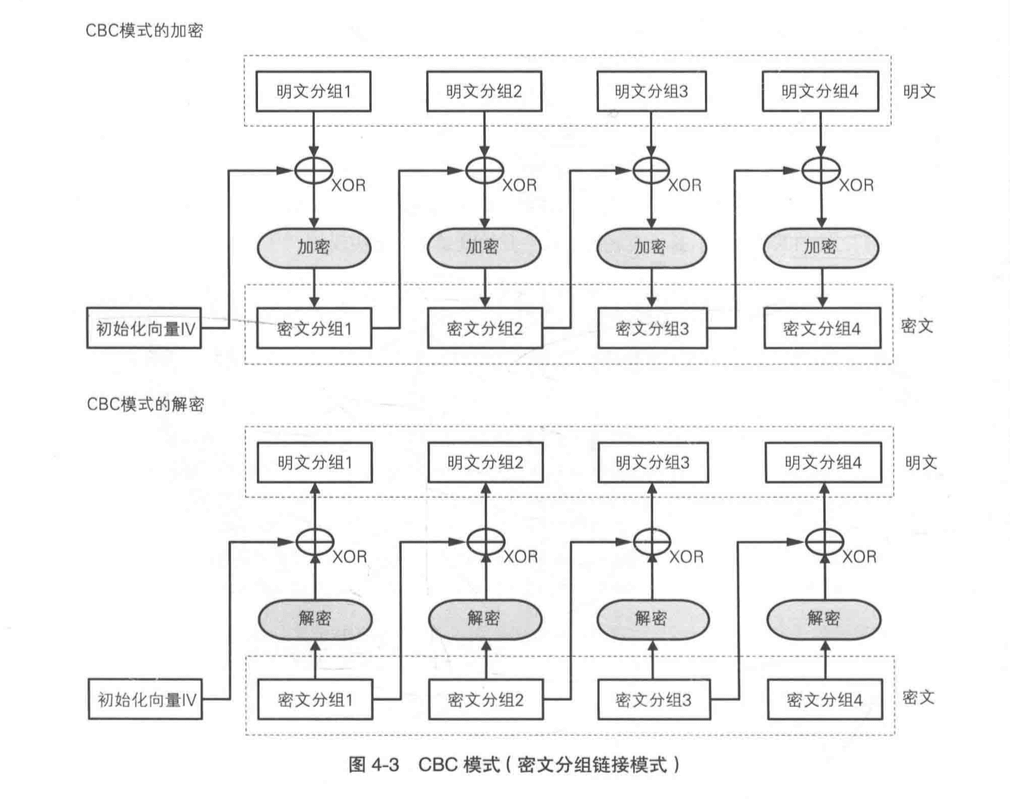
CBC 模式的全称是 Cipher Block Chaining 模式,密文分组链接模式。名字中也展示它的实质,像链条一样相互链接在一起。
CBC 加密“链条”起始于一个初始化向量 IV,这个初始化向量 IV 是一个随机的比特序列。
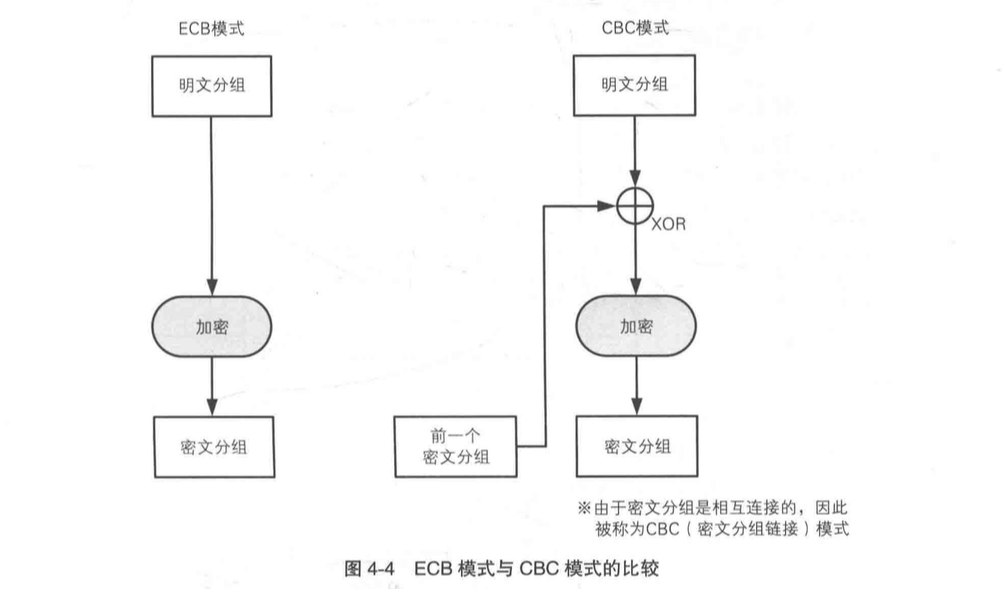
如果把 ECB 单个分组加密抽出来和 CBC 分组对比,如下:
ECB 模式只进行了加密,CBC 模式则在加密之前进行了一次 XOR。这样也就完美了克服了 ECB 的缺点了。比如密文分组 1 和密文分组 2相同,ECB 加密以后 2 个密文分组也是相同的,但是 CBC 加密以后就不存在 2 个密文相同的情况,因为有 XOR 这一步。
CBC 加密必须是从“链条”头开始加密,所以中间任何一个分组都无法单独生成密文。
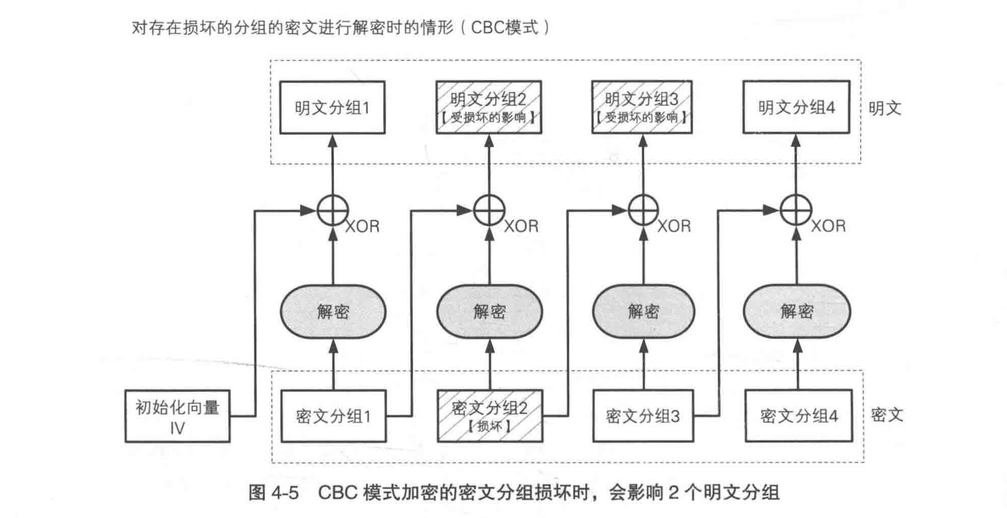
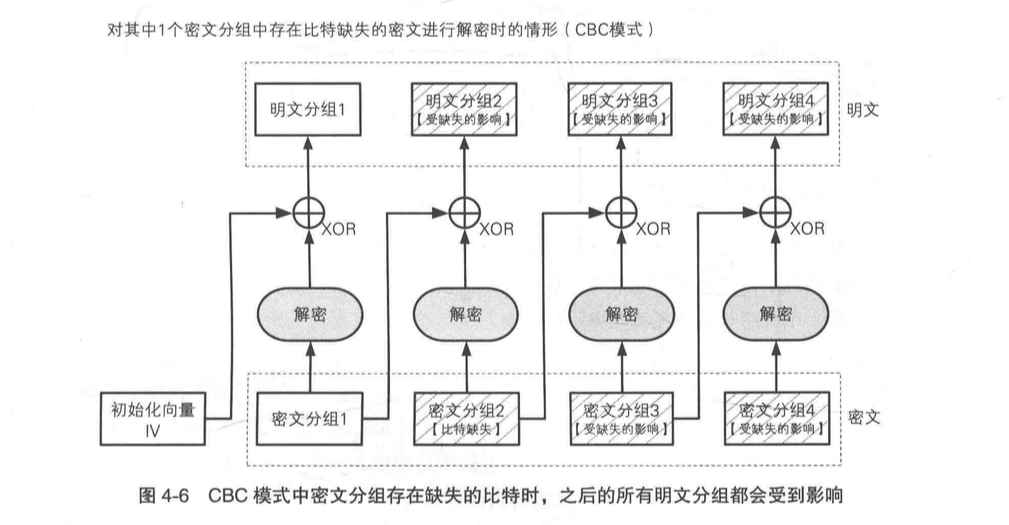
CBC 解密的时候,如果解密“链条”中间有一环“断”了,会出现什么问题呢?
CBC 解密过程中如果有一环出现了问题,硬盘等问题出现了,但是整个链条长度没变,如上图的情况,那么一个坏的环会影响 2 个分组的解密。
如果链条长度也发生变化了,或者某个分组中的 1 个比特位在网络传输过程中缺失了。那么影响的解密分组可能就不止 2 个分组了。因为会引起整个链条上重新分组,这样一来导致原文无法解密(因为位数少于分组要求,解密的时候不会填充末尾分组不足的比特位)。
这一点算是 CBC 链式的一个“小缺点”。一个比特位的缺失会导致整个密文无法解析。
由于 CBC 是链式的,所以攻击者可以考虑从“头”开始攻击,即攻击初始化向量 IV,例如把初始化向量中的某些比特位进行 0,1 反转。这样的话,消息接收者在解密消息的时候,明文 1 分组会受到初始化向量的影响,出现错误。
还有一种攻击办法是直接攻击密文。例如密文分组中的某个分组 n 被改变了,那么就会影响到明文分组 n+1 的解密。
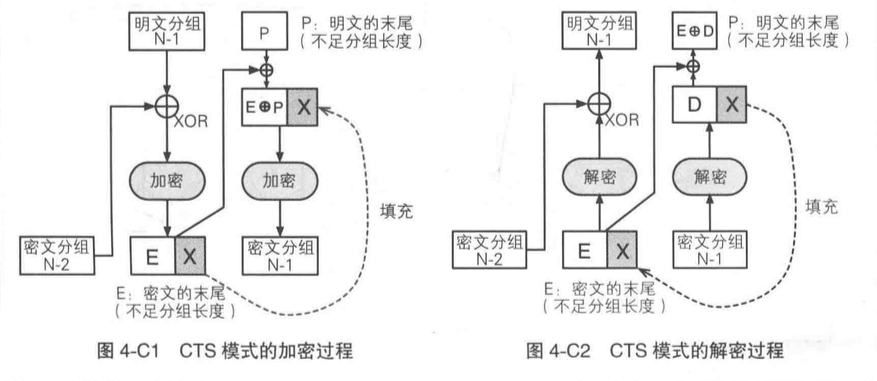
分组密码还存在一种模式叫 CTS 模式(Cipher Text Stealing 模式)。在分组密码中,当明文长度不能被分组长度整除的时候,最后一个分组就需要进行填充,CTS 模式是使用最后一个分组的前一个密文分组数据来进行填充的,它通常和 ECB 模式以及 CBC 模式配合使用。根据最后一个分组的发送顺序不同,CTS 模式有几种不同的变体(CBC-CS1、CBC-CS2、CBC-CS3),下面举一个 CBC-CS3 的例子:
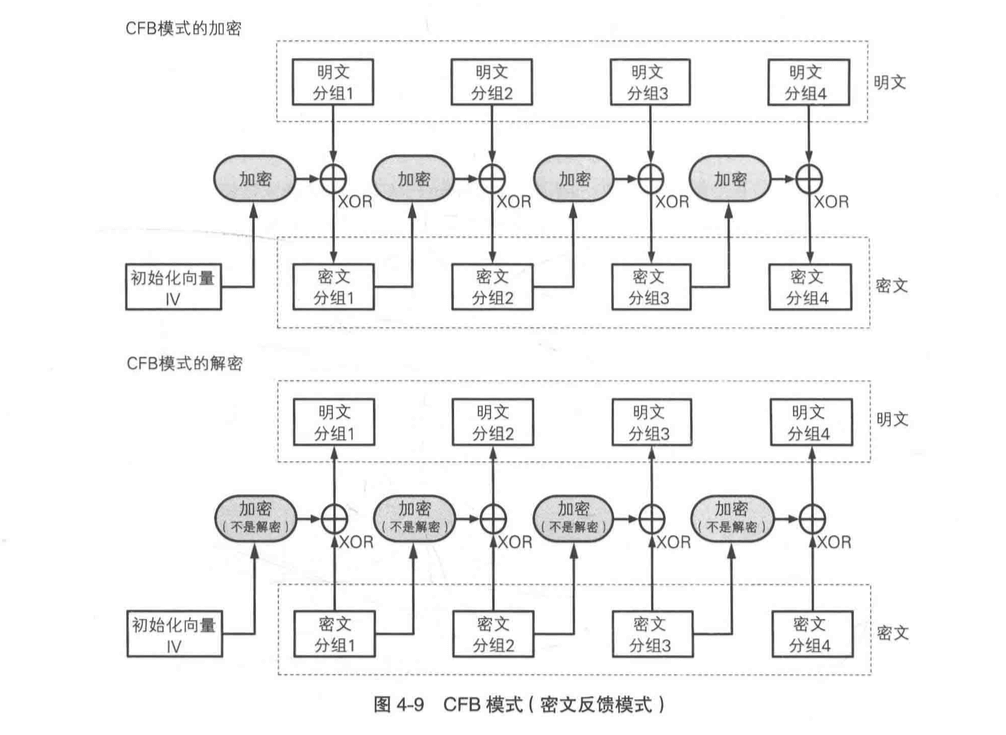
CFB 模式的全程是 Cipher FeedBack 模式(密文反馈模式)。在 CFB 模式中,前一个密文分组会被送到密码算法的输入端。所谓反馈,这里指的就是返回输入端的意思。
注意上图中解密过程,中间是加密而不是解密!因为这里需要保证明文和密文之间异或的对象不变。不变才能异或两次还原明文。
如果把 CBC 单个分组加密抽出来和 CFB 分组对比,如下:
从上图中我们可以看到,在 ECB 和 CBC 模式中,明文分组都是要通过加密算法处理的,但是 CFB 模式明文分组是没有经过加密算法直接加密的。CFB 模式中,明文和一串比特序列 XOR 以后就变成了密文分组。
CFB 整个过程很像一次性密码本,如果把明文分组前的加密部分全部都看成一个随机比特序列,那么就和一次性密码本的流程一样了。这个由算法生成的比特序列称为密钥流。在 CFB 模式中,密码算法就相当于用来生成密钥流的伪随机数生成器,初始化向量相当于是伪随机数生成器的种子。也因为它是伪随机数,所以 CFB 是不具备一次性密码本绝对无法被破译的性质的。所以说,CFB 是一种使用分组密码来实现流密码的方式之一。
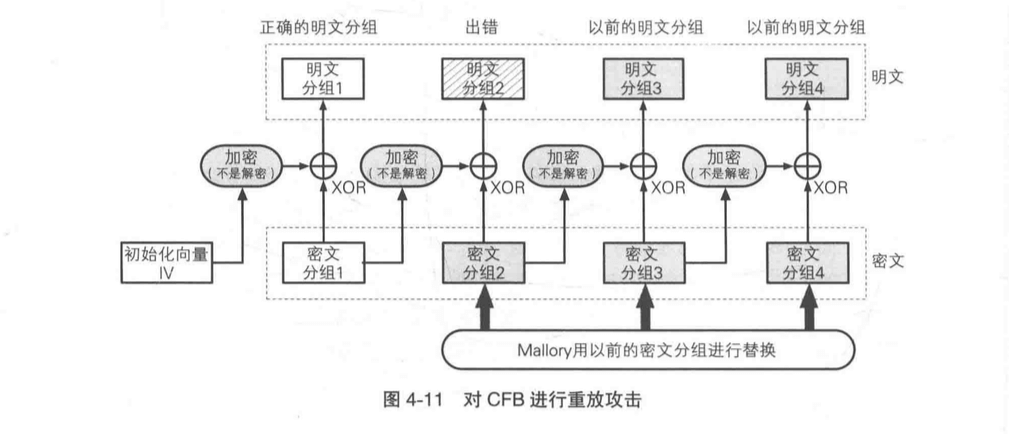
可以对 CFB 实施重放攻击(replay attack)。
例如攻击者可以把上一次会话中的部分分组截取出来放进下次会话随机位置。这样消息接收者在拿到密文以后进行解密,会导致其中一个分组出现错误(上图中是明文分组 2 解密失败),这个时候无法判断是通信出错还是被人攻击所致。(想要判断需要用到消息认证码才行,而此处只是单纯的 CFB)
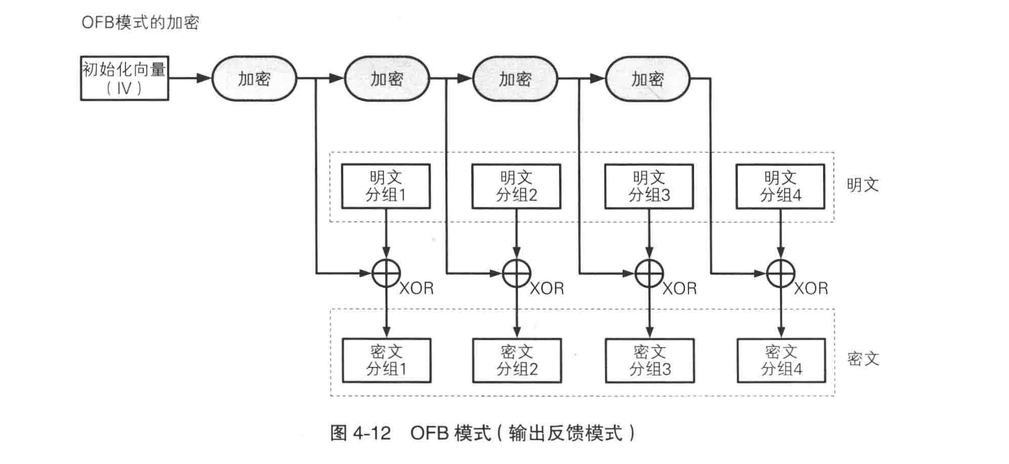
OFB 模式的全程是 Output-FeedBack 模式(输出反馈模式)。在 OFB 模式中,密码算法的输出会反馈到密码算法的输入中。这里可以类比 CFB 模式。
OFB 也不直接对明文进行加密,也是通过利用明文和一串比特序列进行异或运算来得到密文。
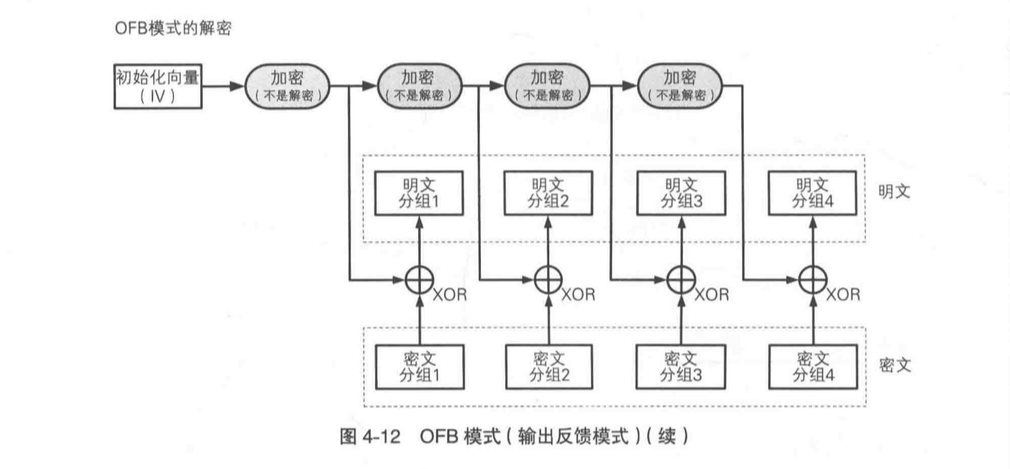
同样需要注意的是,OFB 的解密过程中,也是用加密,而不是解密。原因和 CFB 是一样的。因为异或运算只有异或相当的数才能还原明文。
OFB 模式和 CFB 模式的区别仅仅在于密码算法的输入。OFB 模式是密码算法的输入是前一个密码算法的输出,所以称为输出反馈模式。CFB 模式是把前一个,密文分组输入到密码算法中,所以称为输入反馈模式。下图是两者的对比:
从上图中我们可以看到,CFB 模式加密的过程是无法跳过某个分组对后面的分组加密的。因为它需要按照顺序进行加密。密文分组会重新输入到加密算法中。
而 CFB 模式就不同,加密算法和密文分组完全是分开的,也就是说只要生成好每次 XOR 运算所需的密钥流,就可以“跳跃”加密任意分组了。这个看来,生成密钥流的操作和进行 XOR 运算的操作是可以并行的。
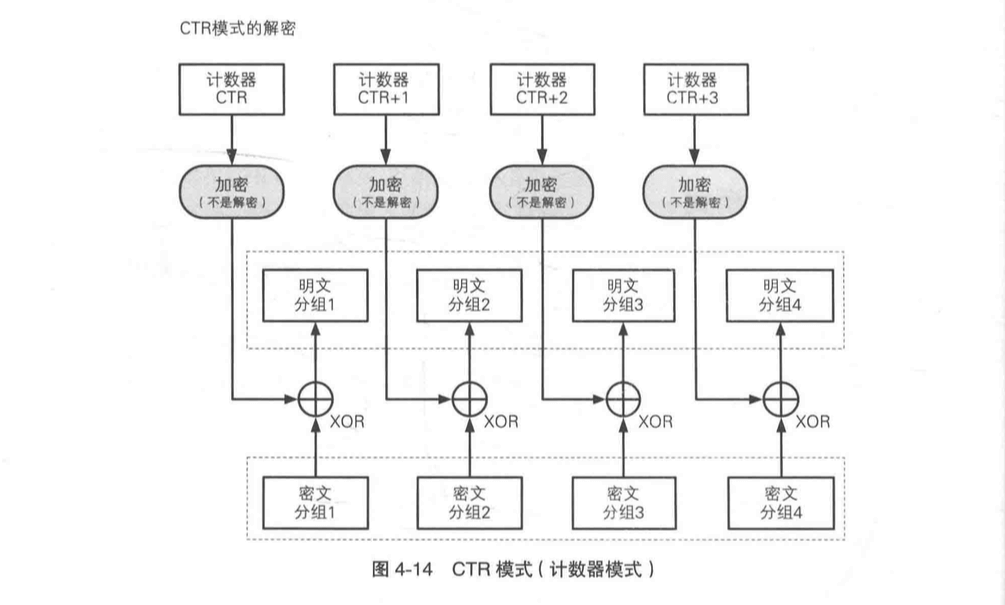
CTR 模式的全程是 CounTeR 模式(计数器模式)。CTR 模式是一种通过将逐次累加的计数器进行加密来生成密钥流的流密码。
注意上图中解密过程,中间是加密而不是解密!因为这里需要保证明文和密文之间异或的对象不变。不变才能异或两次还原明文。
计数器每次都会生成不同的 nonce 来作为计数器的初始值。这样保证每次的值都不同。这种方法就是用分组密码来模拟生成随机的比特序列。
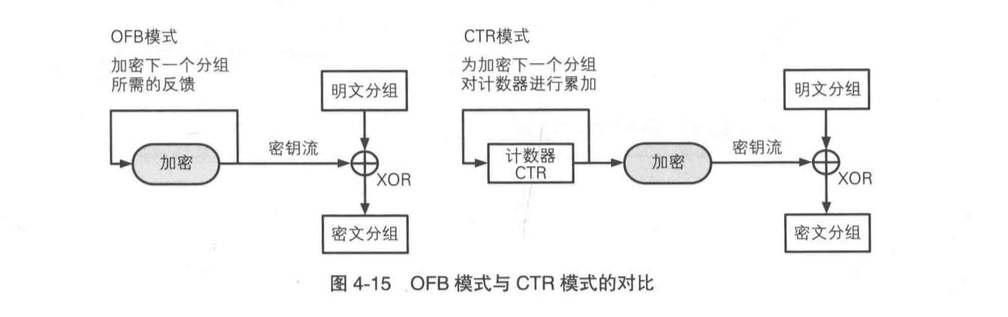
CTR 模式和 OFB 模式都属于流密码。我们单独看两个加密过程,差异在输入到加密算法中的值不一样。CTR 模式输入的值是计数器累加的值,而 OFB 模式输入的值是上一次输出的值。
CTR 模式加密和解密都用了完全相同的结构,这样对程序实现来说,方便很多。更进一步,由于 CTR 模式每个密钥有累加的关系,所以可以通过这个关系,对任意一个分组进行加密和解密。因为只要初始的密钥确定以后,后面的每个密钥都确定了。这样看来,CTR 也是支持并行计算的。
在被攻击方面 CTR 和 OFB 是差不多的。CTR 模式的密文分组中有一个比特被反转了,则解密以后明文分组中仅有与之对应的比特会被反转,这个错误不会被放大。
不过 CTR 模式比 OFB 模式相比有一个更好的优点在于,如果 OFB 模式某次密钥流的一个分组进行加密以后生成的结果和前一次一样,那么这个分组之后的每次密钥流都不变了。CTR 模式就不会存在这一问题。
针对 CTR 模式,在它上面再加上认证功能,就变成了 GCM 模式(Galois/Counter Mode),这个模式能够在 CTR 模式生成密文的同时生成用于认证的信息。从而判断“密文是否通过合法的加密过程生成”。通过这一机制,即便主动攻击者发送伪造的密文,我们也能识别出“这段密文是伪造的”。
| 模式 | 名称 | 特点 | 说明 |
|---|---|---|---|
| ECB 模式 | Electronic Codebook | 运算快速,支持并行运算,需要填充 | 不推荐使用 |
| CBC 模式 | Cipher Block Chaining | 支持并行运算,需要填充 | 推荐使用 |
| CFB 模式 | Cipher Feedback | 支持并行运算,不需要填充 | 不推荐使用 |
| OFB 模式 | Output Feedback | 迭代运算使用流密码模式,不需要填充 | 不推荐使用 |
| CTR 模式 | Counter | 迭代运算使用流密码模式,支持并行运算,不需要填充 | 推荐使用 |
| XTS 模式 | XEX-based tweaked-codebook | 不需要填充 | 用于本地硬盘存储解决方案中 |
$ openssl enc -aes-128-cbc -in in.txt -out out.txt -K 12345678901234567890 -iv 12345678将 in.txt 文件的内容进行加密后输出到 out.txt 中。这里通过 -K 指定密钥,-iv 指定初始向量。注意 AES 算法的密钥和初始向量都是 128 位的,这里 -K 和 -iv 后的参数都是 16 进制表示的,最大长度为 32。 即 -iv 1234567812345678 指定的初始向量在内存中为 | 12 34 56 78 12 34 56 78 00 00 00 00 00 00 00 00 |。
通过 -d 参数表示进行解密 如下
$ openssl enc -aes-128-cbc -in in.txt -out out.txt -K 12345678901234567890 -iv 12345678 -d表示将加密的 in.txt 解密后输出到 out.txt 中
$ openssl enc -aes-128-cbc -in in.txt -out out.txt -pass pass:helloworld这时程序会根据字符串 "helloworld" 和随机生成的 salt 生成密钥和初始向量,也可以用 -nosalt 不加盐。
- RC4 是运算性能最高的流密码对称加密算法
- AES 算法如果能使用 AES-NI 指令集,性能也非常不错,其他的几种加密算法在 HTTPS 协议中使用的很少,性能也很差。
- 普遍认为,AES-128-GCM 性能比 AEC-128-CBC 性能高。
- ChaCha20-poly1305 性能比 AES-128-GCM 性能还要高,大部分情况下认为手机设备更适合 ChaCha20-poly1305 算法。
手机上使用 ChaCha20-poly1305,电脑上使用 AES-128-GCM。
Reference:
《图解密码技术》
GitHub Repo:Halfrost-Field
Follow: halfrost · GitHub