Q:: What is the official term for Big O?
A:: The official term is Big O asymptotic analysis.
Q:: What can big O tell us about a problem?
A:: It can tell us how well a problem is solved.
Q:: What is good code?
A:: Is the code that is:
- Readable (is your code clean? can others understand your code?)
- Scalable (when we grow bigger and bigger with our input how much does the algorithm or function slow down?)
Q:: What is algorithmic efficiency?
A:: The term algorithmic efficiency is used to describe those properties of algorithms that are related to the amount of resources used by the algorithm. Usually referred to as scalability(Big O)
Q:: What does linear time mean?
A:: If an algorithm is in the order of O(n), or linear time complexity, the number of operations it performs scales in direct proportion to the input.
e.g. (for loops, while loops through n items)
Q:: What does constant time mean?
A:: Constant time means that the number of steps/operations does not depend on the input size. Also known as O(1). Predictability is always good
Q:: What does the rule of "worst-case" mean?
A:: It means that we always worry about the worst case, because when we talk about scalability we can never assume that things are going to go well (you don't know how the input is going to be). When we talk about Big O we always talk about the worst case scenario.
Q:: What does the rule of "eliminating constants" mean?
A:: As the name says, if Big 0 is the product of multiple terms, constant terms are eliminated (constant terms are like static numbers, numbers like 1, 4, 5, basically anything that is not a variable).
We only care about when it scales, when the size of the input is getting larger and larger.
Q:: What is the big O of iterating over half a collection?
A:: It ends up being O(n) because if we apply basic mathematics we can transform the division into a multiplication (n/2 = 1/2 x n) and then apply the rule of eliminating constants.
Q:: What does the rule of "different terms for inputs" mean?
A:: It means that different notations/variables are used for different inputs, because since we do not know the length of each one, we cannot assume that they are the same.
- O(n) is different from O(a + b)
- O(n^2) is different from O(a * b)
Q:: When calculating big O and having steps in order (one below the other), which operation should be used?
A:: Addition (+) must be used for steps in order
Q:: When calculating large O and having nested steps (a loop within a loop), which operation should be used?
A:: Multiplication (*) must be used for nested steps.
Q:: What does quadratic time mean?
A:: It means that the number of operations it performs is proportional to the square of the input.
e.g. Every element in a collection needs to be compared to ever other element. Two
nested loops
Q:: What does the rule of "drop non dominants" mean?
A:: It means that we prioritize the term that has more weight (scale) at the moment of calculating the big O.
- O(n^2+3n+100+n/2) is equal to O(n^2)
Q:: What are data structures?
A:: They are a way of storing data.
You could say they are a collection of values and these values can have relationships between them and functions can be applied to them.
The most important thing is that each data structure is good and specialized in its own thing.
Q:: What are algorithms?
A:: These are the steps or processes we put in place to manipulate our data structures to write our programs (instructions for our computer).
Q:: What does factorial time mean?
A:: It means that the number of operations will be proportional to the factorial of the input.
We will find ourselves writing algorithms with factorial time complexity when calculating permutations and combinations.
Factorial is the multiplication of all positive integer numbers less than itself. For instance:
The factorial of 5, or 5!, is:
5 * 4 * 3 * 2 * 1 = 120
Q:: What are the 3 pillars of good coding?
A:: 1. Readable: (clean code) that can be maintained and others can read.
2. Speed: (time complexity) that has a Big O that is efficient, scales well.
3. Memory: (space complexity)
Q:: What causes Space complexity? (how much memory or resources it occupies as the input grows)
A:: 1. Variables (assignments and mutability with objects)
2. Data Structures (both custom and native)
3. Function Call (function calls, e.g. a recursive one, which is stored in memory as a stack.)
4. Allocations (when we create variables, functions or anything else that is stored in the memory)
Q:: What would you say is the Big O in the following sentence?
"asdasdljasdk".length;A:: It depends on the language you are working with, we need to know how the method is implemented to be able to give an accurate answer.
Q:: What can cause time in a function? (how long does it take to traverse / solve something as the input grows, how many operations does it have to perform?)
A:: 1. Operations (+, -, *, /)
2. Comparisons (<, >, ==)
3. Looping (for, while)
4. Outside Function call (function()) (can be a call to a recursive function or to a regular function.)
Q:: List the common Big O complexities from worst to best (there are 7)
A:: O(n!)
O(2^n)
O(n^2)
O(n log n)
O(n)
O(log n)
O(1)
Q:: Space complexity is not concerned with the size of the input per se but the...
A:: ...memory that is being allocated for each operation.
Q:: What skills does the interviewer look for?
A:: 1. Analytic Skills - How can you think through problems and analyze things? - (e.g. can you come up with alternatives to solve the problem?)
2. Coding Skills - Do you code well, by writing clean, simple, organized, readable code? - (e.g. Big O)
3. Technical knowledge - Do you know the fundamentals of the job you're applying for? - (e.g. language JavaScript)
4. Communication skills: Does your personality match the companies’ culture?
Q:: What is the first step when approaching a problem in an interview?
A:: When the interviewer says the question, write down the key points at the top and ensure you have all the details.
Q:: What should you double check after understanding the problem statement in an interview?
A:: Verify the inputs and outputs of the problem.
Q:: What factors should you consider to determine the most important value of the problem in an interview?
A:: Consider time, space, memory, and the main goal of the problem.
Q:: What should you avoid when asking questions during an interview?
A:: Avoid being annoying and asking too many questions.
Q:: What is the initial approach you should start with in an interview?
A:: Start with the naive/brute force approach, demonstrating your ability to think critically.
Q:: Why should you explain why the initial approach is not the best (in an interview)?
A:: Explain limitations such as high time complexity (O(n^2) or higher) or code readability issues.
Q:: What should you analyze when walking through your approach in an interview?
A:: Look for repetitions, bottlenecks (with the highest Big O notation), and unnecessary work. Utilize all the information provided by the interviewer.
Q:: What should you do before starting the coding process in an interview?
A:: Walk through your code and outline the steps you will follow.
Q:: How should you structure your code from the beginning (in an interview)?
A:: Modularize your code into smaller pieces and add comments if necessary.
Q:: When should you start writing the actual code in an interview?
A:: Begin coding once you have a clear understanding of the problem and the steps you need to implement.
Q:: What should you consider while coding to showcase your abilities in an interview?
A:: Break the problem into functions and focus on demonstrating your skills. Even if you forget a specific method, create a function as a placeholder.
Q:: How should you handle error checks in your code during an interview?
A:: Assume people will try to break your code and consider potential false inputs. Safeguard your code and discuss additional checks or tests that could be implemented.
Q:: What naming convention should you follow when writing code in an interview?
A:: Avoid using confusing names like 'i' and 'j.' Write code that is readable and easy to understand.
Q:: What should you do after writing the code in an interview?
A:: Test your code thoroughly, considering different scenarios such as no parameters, zero values, undefined or null inputs, large arrays, and asynchronous code. Look for repetitive sections in your solution.
Q:: What should you discuss with the interviewer after testing the code during an interview?
A:: Share potential improvements, alternative approaches, code readability, and suggestions for performance enhancements. You can also inquire about the most interesting solution the interviewer has encountered for the problem.
Q:: What additional question might an interviewer ask after reviewing your solution?
A:: The interviewer may ask how you would handle the problem if the input is too large to fit into memory or if it arrives as a stream. The typical answer involves a divide-and-conquer approach, performing distributed processing of the data.
Q:: What is the primary requirement for code functionality?
A:: The code should function correctly and solve the problem.
Q:: How does the selection of appropriate data structures impact program efficiency?
A:: By choosing appropriate data structures, programs can achieve efficient data storage and manipulation.
Q:: What should you do to promote code reusability and avoid code duplication?
A:: To promote code reusability and avoid code duplication, you should extract common logic into reusable functions or modules and apply them wherever necessary.
Q:: How does modularity impact code quality?
A:: Modularity improves code quality by enhancing readability, maintainability, and testability.
Q:: Why should nested loops be avoided?
A:: They can be expensive in terms of time complexity. It is better to have separate loops than nesting them.
Q:: What is the recommended complexity for algorithms?
A:: Less than O(N^2). Optimize algorithms to reduce time complexity, avoiding quadratic time complexity or higher.
Q:: What potential issues can arise from recursion?
A:: Recursion can cause stack overflow due to excessive function calls.
Q:: How does copying large arrays affect space complexity?
A:: Copying large arrays may exceed the memory capacity of the machine, leading to potential issues.
Q:: What data structure is often the answer to improve time complexity?
A:: Hash Maps. They can provide efficient lookup and retrieval operations.
Q:: What data structure can be used with a sorted array to achieve O(log N) time complexity?
A:: Binary Tree. It enables divide and conquer techniques, such as binary search, on sorted data sets.
Q:: What technique can be applied to improve performance when working with data?
A:: Sorting the input. It can facilitate more efficient algorithms and operations.
Q:: What are some effective ways to optimize code?
A:: Hash tables and precomputed information (e.g., sorted data) can contribute to code optimization.
Q:: What tradeoff should be considered between time and space?
A:: Consider the Time vs Space tradeoff. Storing extra state in memory can sometimes improve runtime.
Q:: How should you respond when the interviewer gives you advice, tips, or hints?
A:: Follow their advice. Take note of the insights provided by the interviewer.
Q:: How can you address the space-time tradeoff in programming?
A:: Hash tables can often provide a solution, using more space to optimize for faster time.
Q:: What is the importance of communicating your thought process during an interview?
A:: It is crucial to communicate your thought process as much as possible. Each part of the interview matters, and clarity of thinking is valuable.
Q:: What is RAM used for?
A:: RAM is used for immediate data storage and retrieval
Q:: What is a memory address?
A:: It is a reference to a specific memory location
Q:: What is a bit (binary digit)?
A:: A bit (binary digit) is the smallest unit of data that a computer can process and store.
A bit is always in one of two physical states, similar to an on/off light switch. The state is represented by a single binary value, usually a 0 or 1.
Q:: What is a byte?
A:: A byte is a sequence of 8 bits that are treated as a single unit.
Q:: What is a memory controller?
A:: A memory controller is a device that manages the data flow between the CPU and system RAM.
The memory controller acts as the middleman in these operations, ensuring that the proper information is retrieved from the right locations.
The closer the information is to the CPU and the less it has to travel, the faster a program can be executed.
Q:: What is CPU cache?
A:: It is a cache memory that is used to reduce the average memory access time.
It's like a mini RAM integrated in the CPU.
Q:: Why is it said that there are no integers in JavaScript?
A:: There is only the Number data type in JS that represents numbers.
Internally it is implemented as IEEE 754 double precision floating point number.
What it means is that - technically there is no dedicated data type that represents integer numbers.
Practically it means that we can safely use only numbers that are safely representable by the aforementioned standard. And it includes integer values in the range: [-9007199254740991; 9007199254740991]. Both values are defined as constants: Number.MIN_SAFE_INTEGER and Number.MAX_SAFE_INTEGER correspondingly.
Is there or isn't there an integer type in JavaScript?
Q:: What are the actions that can be performed on a data structure?
A:: -
- Insertion: Add a new data item in a given collection of items
- Deletion: Delete data from a collection
- Traversal: Access to each data item exactly once so it can be processed
- Searching: Find the location of the data item if it exists in a given collection
- Sorting: Having data that is sorted
- Access: How do we access this data that we have on our computer
Q:: What are the 2 pillars of Data Structures?
A:: How to build one
How to use one
Q:: What is an array?
A:: An array is a collection of items stored at contiguous memory locations.
Q:: What is the Big O for an Array lookup operation? (aka access: Array[2])
A:: O(1)
Q:: What is the Big O for an Array find operation? (aka search: Array.find(callbackFn))
A:: O(n)
e.g. We traverse the entire array to check if an element is present.
Q:: What is the Big O of an Array push/append operation? (aka insertion: Array.push(value))
A:: O(1) if the array is static
O(n) if the array is dynamic and has to grow when the new value is added.
or if we are using other methods like (shift(), splice())
Note that the worst case is still O(n).
Q:: What is the Big O of an Array shift operation? (aka insertion: Array.shift(value))
A:: O(n)
Q:: What is the Big O of an Array pop operation? (aka deletion: Array.pop())
A:: O(1)
Note that the worst case is still O(n). - (unshift, splice, etc)
Q:: What is the Big O of an Array unshift operation? (aka deletion: Array.unshift())
A:: O(n)
Q:: What are the 2 types of Arrays?
A:: Dynamic and Static
Q:: What is a dynamic array?
A:: An array that can grow in size when it needs to. No specification of size is needed when it is initiated.
Q:: What is a static array?
A:: A fixed size array. Must specify the size when it is initiated.
Q:: In JavaScript, what data structure is an Array actually?
A:: An Object which contains properties and methods which make it Array-like.
Q:: How would you create an array structure?
A:: You may use an object:
class MyArray {
constructor() {
this.length = 0;
this.data = {};
}
get(index) {
return this.data[index];
}
push(item) {
this.data[this.length] = item;
this.length++;
return this.data;
}
pop() {
const lastItem = this.data[this.length - 1];
delete this.data[this.length - 1];
this.length--;
return lastItem;
}
deleteAtIndex(index) {
const item = this.data[index];
this.shiftItems(index);
return item;
}
shiftItems(index) {
for (let i = index; i < this.length - 1; i++) {
this.data[i] = this.data[i + 1];
}
console.log(this.data[this.length - 1]);
delete this.data[this.length - 1];
this.length--;
}
}
const myArray = new MyArray();
myArray.push("hi");
myArray.push("you");
myArray.push("!");
myArray.pop();
myArray.deleteAtIndex(0);
myArray.push("are");
myArray.push("nice");
myArray.shiftItems(0);
console.log(myArray);Q:: How should we handle questions related to strings?
A:: We should treat it as an array question, strings are an array of characters.
e.g. reverse a string.
Q:: What are the pros of using arrays?
A:: 1. Fast lookups (accessing information where you know which index you want to look at)
2. Fast push/pop (adding or removing things at the end of an array)
3. Ordered (having something that is ordered and close to each other in memory makes it really fast)
Q:: What are the cons of using arrays?
A:: 1. Slow inserts (we have to shift the array when at the very end of the array)
2. Slow deletes (same as inserts)
3. Fixed size* (sometimes you have to declare the memory ahead of time and how large of an array you want. Most modern languages have dynamic arrays that help with this)
Q:: What are Hash Tables?
A:: Collections of { Key: Value } pairs
A Hash table is defined as a data structure used to insert, look up, and remove key-value pairs quickly.
It operates on the hashing concept, where each key is translated by a hash function into a distinct index in an array. The index functions as a storage location for the matching value. In simple words, it maps the keys with the value. (it will store the key and the value at the same address in memory - a "bucket")
Input = Grape
Output (is always) = G7xpLLQ4
G7xpLLQ4 -> key:value
Q:: What is a Hash function?
A:: A function that generates a value of fixed length for each input it receives. For any given input, the output will always be the same.
Examples:
Input = Grape
Output (is always) = G7xpLLQ4
Input = 5
Output (is always) = Ax67def0
Q:: What does it mean for a function to be "idempotent"?
A:: It is a fancy way of saying that a function given an input always outputs the same output
Q:: What is the Big O for insertion into a Hash Table?
A:: O(1)
Unless there is a collision, then it would be O(n).
Q:: What is the Big O for a lookup (access) in a Hash Table?
A:: O(1)
Unless there is a collision, then it would be O(n).
Q:: What is the Big O for deletion in a Hash Table?
A:: O(1)
Unless there is a collision, then it would be O(n).
Q:: What is the Big O for a search in a Hash Table?
A:: O(1)
e.g. object["key"] It will return if that key is present in the object (undefined otherwise), that's why it is O(1).
Unless there is a collision, then it would be O(n).
Q:: What is a collision in regards to a Hash Table?
A:: When a new item is added to the same "address" as an already existing item in a Hash Table.
This could slow down the lookup for a Hash Table from O(1) to O(n).
Q:: What kind of data-type is a Key in a typical Hash Table?
A:: A String
Q:: In ES6, what kind of data-types can a Key be for a Map?
A:: Any kind of data-type
Q:: In ES6, what kind of Hash Table maintains insertion order?
A:: A Map
Q:: Does a Set store values in JavaScript?
A:: No, only Keys which are unique (no two keys can be the same in a Set).
Q:: How would you create an object structure?
A:: You may use an array:
class HashTable {
constructor(size) {
this.data = new Array(size);
// this.data = [];
}
_hash(key) {
let hash = 0;
for (let i = 0; i < key.length; i++) {
hash = (hash + key.charCodeAt(i) * i) % this.data.length;
}
return hash;
}
set(key, value) {
let address = this._hash(key);
if (!this.data[address]) {
this.data[address] = [];
}
this.data[address].push([key, value]);
return this.data;
}
get(key) {
const address = this._hash(key);
const currentBucket = this.data[address];
if (currentBucket) {
for (let i = 0; i < currentBucket.length; i++) {
if (currentBucket[i][0] === key) {
return currentBucket[i][1];
}
}
}
return undefined;
}
}
const myHashTable = new HashTable(50);
myHashTable.set("grapes", 10000);
myHashTable.get("grapes");
myHashTable.set("apples", 9);
myHashTable.get("apples");Q:: Which data-structure is more efficient at looping over data: An Array or a Hash Table?
A:: An Array.
If your Hash Table has 50 addresses but only 3 addresses contain Keys, you would still have to access all 50 addresses to obtain those Keys.
An Array is sequential in memory, which makes it more efficient in this regard.
Q:: What are the pros of using hash tables?
A:: 1. Fast lookups* (Good collision resolution needed, usually we dont need to worry about this because our language underneath the hood take care of that for us)
2. Fast inserts (same as lookups)
3. Flexible keys (depending on the type of hash tables, such as maps, we can have flexibles keys instead of an array that has numbered indexes)
Q:: What are the cons of using hash tables?
A:: 1. Unordered (its hard to really go through everything in order)
2. Slow key iteration (if i want to grab all the keys from a hash table I will have to go through the entire memory space)
Q:: Can Linked Lists help solve collision issues in a Hash Table?
A:: Yes
Q:: What is a Linked List?
A:: A collection of nodes and pointers.
Data is stored in the node itself and a pointer is a reference to the next node in the list.
The end of a Linked List is signified by a "null" value.
Q:: How its called the first node in a linked list?
A:: Head.
Q:: How its called the last node in a linked list?
A:: Tail.
Some people call the tail anything that is after the head.
Q:: How do you know that you have reached the end of a Linked List?
A:: Linked Lists are "null-terminated" which means the end of the list is denoted by the value "null".
Q:: What kind of structure do Linked Lists have?
A:: A 'loose' structure. You can easily insert a new data as you only have to change 2 pointers (depending on if it is singly linked, doubly linked, etc..)
Q:: What is the main difference between a Linked List and an Array?
A:: Arrays are indexed, Linked Lists are not.
If you want to access the 5th element in a Linked List, you have to start from the beginning of the list and traverse to the 5th element.
In an Array, you can simply access the element at index 4 ( arr[4] ) to get the value of the 5th element.
Q:: Are nodes in a Linked List stored sequentially in memory?
A:: No. They are scattered over memory which makes traversal of a Linked List slower than traversal of an Array.
Q:: Whats one advantage that linked list have over hash tables?
A:: That there is some sort of order to link list, each node points to the next node.
Q:: What is the Big O for a prepend (add to the beginning of the list) operation on a Linked List/Double link list?
A:: O(1)
Q:: What is the Big O of an append (add to the end of the list) operation on a Linked List/Double link list?
A:: O(1)
Q:: What is the Big O of a lookup (traversal) operation on a Linked List/Double link list?
A:: O(n)
e.g. We go through the whole linked list to check if an element is present. In the case of a double linked list it would technically be O(n/2) because we can start at both ends and if we know in which half of the list is what we are looking for, we can choose the optimal place to start.
Q:: What is the Big O of an insertion operation on a Linked List/Double link list?
A:: O(n)
Q:: What is the Big O of a deletion operation on a Linked List/Double link list?
A:: O(n)
Q:: What is a pointer?
A:: A pointer is a reference to another place in a memory (another node). Kind of like a variable referencing another variable.
Q:: What does a Doubly Linked List have that a Singly Linked List does not?
A:: A 'previous' pointer which references the node before it. You can traverse forwards and backwards through a Doubly Linked List. You can only traverse forwards in a Singly Linked List.
Q:: Does a Doubly Linked List use more memory than a Singly Linked List?
A:: Yes. The 'previous' pointer will require more memory for the Doubly Linked List to be implemented.
Q:: How would you create a double linked list structure?
A:: -
class DoublyLinkedList {
constructor(value) {
this.head = {
value: value,
next: null,
prev: null,
};
this.tail = this.head;
this.length = 1;
}
append(value) {
const newNode = {
value: value,
next: null,
prev: null,
};
console.log(newNode);
newNode.prev = this.tail;
this.tail.next = newNode;
this.tail = newNode;
this.length++;
return this;
}
prepend(value) {
const newNode = {
value: value,
next: null,
prev: null,
};
newNode.next = this.head;
this.head.prev = newNode;
this.head = newNode;
this.length++;
return this;
}
printList() {
const array = [];
let currentNode = this.head;
while (currentNode !== null) {
array.push(currentNode.value);
currentNode = currentNode.next;
}
return array;
}
insert(index, value) {
//Check for proper parameters;
if (index >= this.length) {
return this.append(value);
}
const newNode = {
value: value,
next: null,
prev: null,
};
const leader = this.traverseToIndex(index - 1);
const follower = leader.next;
leader.next = newNode;
newNode.prev = leader;
newNode.next = follower;
follower.prev = newNode;
this.length++;
console.log(this);
return this.printList();
}
traverseToIndex(index) {
//Check parameters
let counter = 0;
let currentNode = this.head;
while (counter !== index) {
currentNode = currentNode.next;
counter++;
}
return currentNode;
}
}
let myLinkedList = new DoublyLinkedList(10);
myLinkedList.append(5);
myLinkedList.append(16);
myLinkedList.prepend(1);
myLinkedList.insert(2, 99);
// myLinkedList.insert(20, 88)
// myLinkedList.printList()
// myLinkedList.remove(2)
// myLinkedList.reverse()Q:: What is an advantage of a linked list over a double linked list in terms of implementation complexity?
A:: A linked list offers a relatively simpler implementation compared to a double linked list.
Q:: How does a linked list compare to a double linked list in terms of memory usage and performance during operations like deletion and insertion?
A:: Linked lists require less memory and exhibit slightly faster performance during operations like deletion and insertion, as there are fewer operations involved and no need to move around the previous property.
Q:: What is a disadvantage of a linked list compared to a double linked list in terms of iteration and traversal?
A:: A linked list cannot be iterated in reverse or traversed from back to front.
Q:: What scenario can lead to the linked list being lost in memory forever?
A:: If the reference to this.head of the list is lost, it can result in the linked list being lost in memory permanently.
Q:: What are the advantages of a double linked list in terms of iteration or traversal?
A:: A double linked list allows iteration or traversal from both the front and the back.
Q:: How does a double linked list facilitate easy insertion or deletion, particularly when deleting a previous node?
A:: In a double linked list, there is no need to traverse from the head node to find the previous node when deleting; thus, deletion becomes easier.
Q:: What impact does the extra property of a double linked list have?
A:: The additional property requires higher memory and storage usage.
Q:: What extra difficulty do the operations (insert, delete) in a double linked list bring?
A:: Due to the presence of the "previous" pointer, additional operations must be performed when inserting or deleting.
Q:: What are the advantages of using linked lists in terms of insertion and deletion speed?
A:: Linked lists offer fast insertion and deletion, particularly when a reference to the desired location is available, avoiding the need for excessive copying or resizing.
Q:: How does a linked list facilitate ordered data?
A:: Linked lists allow for maintaining ordered data.
Q:: Why is a linked list considered flexible in terms of size?
A:: Linked lists are flexible in size, meaning they can grow and shrink dynamically as needed.
Q:: What is the primary reason for choosing a linked list over an array?
A:: The primary reason for choosing a linked list over an array is its simplicity and the ability to adjust its size as required.
Q:: What is a disadvantage of using linked lists in terms of lookup speed?
A:: Linked lists suffer from slow lookup because traversal through the list is necessary when searching for a specific element.
Q:: How does the usage of linked lists impact memory usage, especially in the case of a double linked list?
A:: Using linked lists requires more memory, particularly in the case of a double linked list, where additional properties such as value, next, and prev need to be stored for each node.
Q:: How would you create a linked list structure?
A:: -
class LinkedList {
constructor(value) {
this.head = {
value: value,
next: null,
};
this.tail = this.head;
this.length = 1;
}
append(value) {
const newNode = {
value: value,
next: null,
};
console.log(newNode);
this.tail.next = newNode;
this.tail = newNode;
this.length++;
return this;
}
prepend(value) {
const newNode = {
value: value,
next: null,
};
newNode.next = this.head;
this.head = newNode;
this.length++;
return this;
}
printList() {
const array = [];
let currentNode = this.head;
while (currentNode !== null) {
array.push(currentNode.value);
currentNode = currentNode.next;
}
return array;
}
insert(index, value) {
//Check for proper parameters;
if (index >= this.length) {
console.log("yes");
return this.append(value);
}
const newNode = {
value: value,
next: null,
};
const leader = this.traverseToIndex(index - 1);
const holdingPointer = leader.next;
leader.next = newNode;
newNode.next = holdingPointer;
this.length++;
return this.printList();
}
traverseToIndex(index) {
//Check parameters
let counter = 0;
let currentNode = this.head;
while (counter !== index) {
currentNode = currentNode.next;
counter++;
}
return currentNode;
}
remove(index) {
// Check Parameters
const leader = this.traverseToIndex(index - 1);
const unwantedNode = leader.next;
leader.next = unwantedNode.next;
this.length--;
return this.printList();
}
reverse() {
if (!this.head.next) {
return this.head;
}
let first = this.head;
this.tail = this.head;
let second = first.next;
while (second) {
const temp = second.next;
second.next = first;
first = second;
second = temp;
}
this.head.next = null;
this.head = first;
return this.printList();
}
}
let myLinkedList = new LinkedList(10);
myLinkedList.append(5);
myLinkedList.append(16);
myLinkedList.prepend(1);
myLinkedList.printList();
myLinkedList.insert(2, 99);
myLinkedList.insert(20, 88);
myLinkedList.printList();
myLinkedList.remove(2);
myLinkedList.reverse();Q:: What kind of data-structure are Stack and Queues?
A:: Linear data-structures. They must be traversed one by one.
Q:: What is the difference between a Stack and a Queue?
A:: The order in which the elements are processed.
A Stack pops the most recent element from the top (Last In First Out)
A Queue processes the first element that went in (First In First Out)
Q:: What is the Big O for a lookup operation in a Stack?
A:: O(n)
Q:: What is the Big O for a pop operation in a Stack?
A:: O(1)
Q:: What is the Big O for a push operation in a Stack?
A:: O(1)
Q:: What is the Big O for a peek operation in a Stack? (view the top of the stack)
A:: O(1)
Q:: What does LIFO stand for in regard to a Stack?
A:: Last In First Out
Q:: What is the Big O for a lookup operation in a Queue?
A:: O(n)
Q:: What is the Big O for a enqueue operation in a Queue?
A:: O(1)
Q:: What is the Big O for a dequeue operation in a Queue?
A:: O(1) - If you did not use an Array to implement the queue.
An Array unshift operation would be O(n).
Q:: What is the Big O for a peek operation in a Queue? (see who is the fist in the queue)
A:: O(1)
Q:: What does FIFO stand for in regards to a Queue?
A:: First In First Out
Q:: What is a program?
A:: Well a program has to do some simple things.
- It has to allocate memory. Otherwise we would be able to have variables or even have a file on our computer.
- It also has to parse and execute scripts which means read and run commands.
Q:: How many parts has a engine (javascript)?
A:: Now the engine consists of two parts a memory heap and a call stack.
- Now the memory heap. This is where the memory allocation happens.
- And then the call stack. This is where your code is read and execute it. It tells you where you are in the program.
Q:: What is a memory leak?
A:: Memory leak occurs when programmers create a memory in heap and forget to delete it.
Q:: What does it mean that javascript is a single threaded language that can be nonblocking?
A:: Single threaded means that it has only one call stack. And one call stack only you can only do one thing at a time Now other languages can have multiple calls. And these are called multi-thread.
Q:: Why was javascript designed to be single threaded?
A:: While running code on a single thread can be quite easy since you don't have to deal with complicateda scenarios that arise in multithreaded environment. You just have one thing to worry about.
Q:: What is a deadlock?
A:: A deadlock is a situation where a set of processes are blocked because each process is holding a resource and waiting for another resource acquired by some other process.
Q:: How would you create a stack structure using a linked list?
A:: -
class Node {
constructor(value) {
this.value = value;
this.next = null;
}
}
class Stack {
constructor() {
this.top = null;
this.bottom = null;
this.length = 0;
}
peek() {
return this.top;
}
push(value) {
const newNode = new Node(value);
if (this.length === 0) {
this.top = newNode;
this.bottom = newNode;
} else {
const holdingPointer = this.top;
this.top = newNode;
this.top.next = holdingPointer;
}
this.length++;
return this;
}
pop() {
if (!this.top) {
return null;
}
if (this.top === this.bottom) {
this.bottom = null;
}
const holdingPointer = this.top;
this.top = this.top.next;
this.length--;
return this;
}
//isEmpty
}
const myStack = new Stack();
myStack.peek();
myStack.push("google");
myStack.push("udemy");
myStack.push("discord");
myStack.peek();
myStack.pop();
myStack.pop();
myStack.pop();
//Discord
//Udemy
//googleQ:: How would you create a stack structure using an array?
A:: -
class Stack {
constructor() {
this.array = [];
}
peek() {
return this.array[this.array.length - 1];
}
push(value) {
this.array.push(value);
return this;
}
pop() {
this.array.pop();
return this;
}
}
const myStack = new Stack();
myStack.peek();
myStack.push("google");
myStack.push("udemy");
myStack.push("discord");
myStack.peek();
myStack.pop();
myStack.pop();
myStack.pop();
//Discord
//Udemy
//googleQ:: How would you create a queue structure using a linked list?
A:: -
class Node {
constructor(value) {
this.value = value;
this.next = null;
}
}
class Queue {
constructor() {
this.first = null;
this.last = null;
this.length = 0;
}
peek() {
return this.first;
}
enqueue(value) {
const newNode = new Node(value);
if (this.length === 0) {
this.first = newNode;
this.last = newNode;
} else {
this.last.next = newNode;
this.last = newNode;
}
this.length++;
return this;
}
dequeue() {
if (!this.first) {
return null;
}
if (this.first === this.last) {
this.last = null;
}
const holdingPointer = this.first;
this.first = this.first.next;
this.length--;
return this;
}
//isEmpty;
}
const myQueue = new Queue();
myQueue.peek();
myQueue.enqueue("Joy");
myQueue.enqueue("Matt");
myQueue.enqueue("Pavel");
myQueue.peek();
myQueue.dequeue();
myQueue.dequeue();
myQueue.dequeue();
myQueue.peek();Q:: How would you create a queue using 2 stacks?
A:: -
class CrazyQueue {
constructor() {
this.first = [];
this.last = [];
}
enqueue(value) {
const length = this.first.length;
for (let i = 0; i < length; i++) {
this.last.push(this.first.pop());
}
this.last.push(value);
return this;
}
dequeue() {
const length = this.last.length;
for (let i = 0; i < length; i++) {
this.first.push(this.last.pop());
}
this.first.pop();
return this;
}
peek() {
if (this.last.length > 0) {
return this.last[0];
}
return this.first[this.first.length - 1];
}
}
const myQueue = new CrazyQueue();
myQueue.peek();
myQueue.enqueue("Joy");
myQueue.enqueue("Matt");
myQueue.enqueue("Pavel");
myQueue.peek();
myQueue.dequeue();
myQueue.dequeue();
myQueue.dequeue();
myQueue.peek();Q:: What are the pros of using stacks and queues?
A:: 1. Fast operations (such as removing or inserting, such as the end of the data structure)
2. Fast peek (we can access the very first item in a queue or the very top item in a stack)
3. Ordered (we have all our data ordered)
Q:: What are the cons of using stacks and queues?
A:: 1. Slow lookup (we dont usually use ours stack or queues to do any sort of look up or search through the data structure, all we are interested in is the end bits of the data structure)
Q:: What is a Tree data-structure?
A:: A hierarchical data-structure consisting of a root node and parent/child nodes.
A Linked List is technically a type of Tree but it is linear instead of having multiple 'branches' or paths.
Q:: What is a abstract syntax tree?
A:: This is how programs and code is usually run
Q:: What is the rule for implementing a Binary Tree?
A:: Each node can have a max of 2 children.
So a node can have 0, 1, or 2 children.
And each child can only have one parent
Each node represent a certain state
Q:: What is a perfect binary tree?
A:: A perfect binary tree has everything filled in, that means that all the leaf nodes are full and there is no node that only has one child, a node either has zero or two children. Also, the bottom layer of the tree is completely filled, nothings is missing
Q:: What is a full binary tree?
A:: A full binary tree says that a node has either 0 or 2 children, but never one child
Q:: What properties does a perfect binary tree has?
A:: 1. The number of total nodes doubles as we move down the tree
2. The number of nodes on the last level is equal to the sum of the number of nodes on all the other levels plus 1
Level 0: 2^0 = 1
Level 1: 2^1 = 2
Level 2: 2^2 = 4
Level 3: 2^3 = 8
Based on that formula, we can find the number of nodes in a tree:
# of nodes = 2^h - 1 (h is the level, starts from count of 1) log nodes = height/steps (simplified version) log 100 = 2 10^2 = 100
Q:: What is the time complexity for a perfect binary tree's search(lookup), insert, and delete methods?
A:: O(log n)
Q:: What does logarithmic time mean?
A:: All that is saying is that the choice of the next element on which to perform some sort of action is one of several possibilities and only one needs to be chosen.
e.g. (usually searching algorithms have log n if they are sorted (Binary Search))
Q:: What is a binary search tree?
A:: BSTs excel at preserving relationships, making them suitable for scenarios where maintaining order and structure is important.
For instance, while a hash table lacks such relationships, organizing folders on a computer necessitates a hierarchical structure with parent and subfolders, which can be achieved using a binary search tree.
- In a BST, all child nodes to the right of a root node must have values greater than the current node. This implies that moving to the right within the tree leads to nodes with increasing values, while moving to the left results in nodes with decreasing values.
- Due to its nature as a binary tree, each node in a BST can have a maximum of two children.
Q:: If a binary tree is unbalanced, what is its worst case time complexity?
A:: O(n) for lookup(search), insert and delete
Q:: How does a binary tree become unbalanced?
A:: A binary tree becomes unbalanced when new nodes are continually placed to the right of one node and its children or to the left of one node and its children (as opposed to spreading them out evenly to keep the left and right sides about the same height, the tree becomes really long on on side).
Q:: How can you tell if a binary tree is balanced?
A:: A binary tree is balanced when every node has roughly the same amount of children.
Q:: What are the pros of using BSTs?
A:: 1. Better than O(n) (most operations are log n, assuming that the BST is balanced)
2. Ordered
3. Flexible size (because we can place a node anywhere in memory we can just have flexible size , we can keep growing our tree)
Q:: What are the cons of using BSTs?
A:: 1. No O(1) operations (we usually have to do some sort of traversal for any sort of operation)
Q:: What does divide and conquer refers to?
A:: Divide and conquer simply means we are dividing up so that we dont visit all the nodes, each node that we visit we make a decision to go left or right
Q:: How would you create a BST structure?
A:: -
class Node {
constructor(value) {
this.left = null;
this.right = null;
this.value = value;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
insert(value) {
const newNode = new Node(value);
if (this.root === null) {
this.root = newNode;
} else {
let currentNode = this.root;
while (true) {
if (value < currentNode.value) {
//Left
if (!currentNode.left) {
currentNode.left = newNode;
return this;
}
currentNode = currentNode.left;
} else {
//Right
if (!currentNode.right) {
currentNode.right = newNode;
return this;
}
currentNode = currentNode.right;
}
}
}
}
lookup(value) {
if (!this.root) {
return false;
}
let currentNode = this.root;
while (currentNode) {
if (value < currentNode.value) {
currentNode = currentNode.left;
} else if (value > currentNode.value) {
currentNode = currentNode.right;
} else if (currentNode.value === value) {
return currentNode;
}
}
return null;
}
remove(value) {
if (!this.root) {
return false;
}
let currentNode = this.root;
let parentNode = null;
while (currentNode) {
if (value < currentNode.value) {
parentNode = currentNode;
currentNode = currentNode.left;
} else if (value > currentNode.value) {
parentNode = currentNode;
currentNode = currentNode.right;
} else if (currentNode.value === value) {
//We have a match, get to work!
//Option 1: No right child:
if (currentNode.right === null) {
if (parentNode === null) {
this.root = currentNode.left;
} else {
//if parent > current value, make current left child a child of parent
if (currentNode.value < parentNode.value) {
parentNode.left = currentNode.left;
//if parent < current value, make left child a right child of parent
} else if (currentNode.value > parentNode.value) {
parentNode.right = currentNode.left;
}
}
//Option 2: Right child which doesnt have a left child
} else if (currentNode.right.left === null) {
currentNode.right.left = currentNode.left;
if (parentNode === null) {
this.root = currentNode.right;
} else {
//if parent > current, make right child of the left the parent
if (currentNode.value < parentNode.value) {
parentNode.left = currentNode.right;
//if parent < current, make right child a right child of the parent
} else if (currentNode.value > parentNode.value) {
parentNode.right = currentNode.right;
}
}
//Option 3: Right child that has a left child
} else {
//find the Right child's left most child
let leftmost = currentNode.right.left;
let leftmostParent = currentNode.right;
while (leftmost.left !== null) {
leftmostParent = leftmost;
leftmost = leftmost.left;
}
//Parent's left subtree is now leftmost's right subtree
leftmostParent.left = leftmost.right;
leftmost.left = currentNode.left;
leftmost.right = currentNode.right;
if (parentNode === null) {
this.root = leftmost;
} else {
if (currentNode.value < parentNode.value) {
parentNode.left = leftmost;
} else if (currentNode.value > parentNode.value) {
parentNode.right = leftmost;
}
}
}
return true;
}
}
}
}
const tree = new BinarySearchTree();
tree.insert(9);
tree.insert(4);
tree.insert(6);
tree.insert(20);
tree.insert(170);
tree.insert(15);
tree.insert(1);
tree.remove(170);
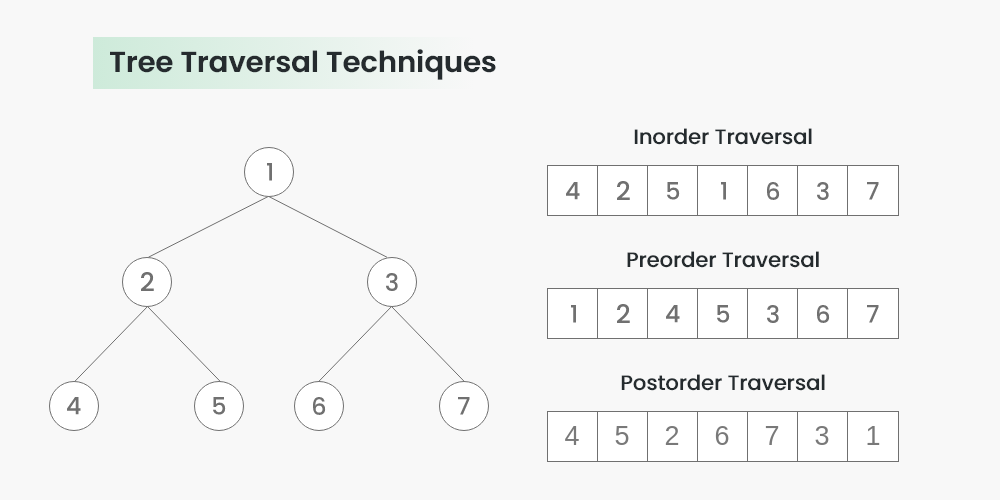
JSON.stringify(traverse(tree.root));
// 9
// 4 20
//1 6 15 170
function traverse(node) {
const tree = { value: node.value };
tree.left = node.left === null ? null : traverse(node.left);
tree.right = node.right === null ? null : traverse(node.right);
return tree;
}Q:: What type of specialized binary trees can you use to maintain balance in a binary tree?
A:: An AVL tree or a Red/Black tree.
Q:: For an AVL tree, what is the equation of the balance factor?
A:: -
|h1 - h2| <= 1 (Balance factor)
|h1 - h2| can be equal to -1,0, or 1.
h1 and h2 are subtrees of the same node.
The balance factor determines whether or not any given subtree of a tree is balanced.
Q:: How many types of node-swapping operations does an AVL tree have to balance itself? What are they?
A:: 2 types of node-swapping operations:
Single Rotations and Double Rotations.
Q:: What are the 4 rules of a Red/Black Binary Tree?
A:: 1. Each node must be either Red or Black
2. Root node must always be black
3. A red node must always have a black parent node and black child nodes
4. Every branch path (the path from root node to an empty leaf node [null]) must posess the exact same number of black nodes.
Extras:
A null leaf node is always considered to be black, even if it is marked red.
A chain of 3 nodes can never be a valid Red/Black Tree.
Q:: What is a binary heap?
A:: A binary heap is a binary tree with the following properties:
- It's a complete tree. All levels are completely filled except possibly the last level, which will have elements positioned as left as possible.
- It is either a Min Heap or a Max Heap.
In a Min Heap the root element must be the smallest (or the one with the least importance) among all elements present in the tree.
In a Max Heap the root element must be the largest (or the one with the higher importance) of all elements present in the tree. - And have a max of 2 children (like a BT)
Q:: What is the Big O for a lookup(search) operation in a Binary Heap?
A:: O(n) (because is less ordered than a than a BST, in this data structure left and right can be any value)
Q:: What is the Big O for an insertion operation in a Binary Heap?
A:: O(log n) - O(1) in the best scenario, but if the order is broken it is possible to bubble upwards and this would result in the worst case (log n).
Q:: What is the Big O for a deletion operation in a Binary Heap?
A:: O(log n)
Q:: Where a BH (binary heap) can be used?
A:: A BH can be used in any algorithm where ordering is important.
Q:: What data-structure are Binary Heaps typically used to implement?
A:: A Priority Queue, data storage, sorting algorithms
Q:: For what BH (binary heap) are good?
A:: They are great at doing comparative operations
e.g. I want people that have a value over 33
Q:: Is a Binary Heap always balanced?
A:: Yes. Insertion order is left to right so they easily preserve their insertion order as well.
Q:: What is a priority queue?
A:: Is similar to a queue but with the difference that there are "vips" or higher priority values that usually take the first or last positions.
Q:: What are the pros of using BH?
A:: 1. Better than O(n)
2. Priority (searching may be slow, but you have an idea of priority, because insertion is done in order)
3. Flexible size
4. Fast insert (we might have to bubble up inserts every once in a while. But most of the time you get really fast inserts)
Q:: What are the cons of using BH?
A:: 1. Slow lookup (it must be taken into account that many times there is a method to find the minimum or maximum which is O(1) - (it all depends if it is a min heap or max heap))
Q:: What is a Trie (aka prefix tree)?
A:: A Trie is a unique type of tree that is an efficient infromation retrieval data structure. It commonly uses alphabetical characters to store data, like words. Often used to implement auto-correct for typing.
In most cases it can outperform BSTs, hash tables and most others data structures. It will depend on what type of search we are doing
Q:: What is a Graph?
A:: A Graph is a non-linear data structure consisting of nodes and edges. The nodes are sometimes referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph.
Technically Trees and Linked Lists are types of a Graph.
Q:: What is a directed graph?
A:: A graph whose nodes (vertexes) point in one direction. Like a one-way street going to the next node (vertex).
Q:: What is an undirected graph?
A:: A graph whose nodes (vertexes) have no defined direction. A node (vertex) can only link to another node (vertex) if that other node (vertex) is also aware of the first node (vertex).
Think of how Facebook works with friends. You cannot be someones friend on Facebook unless they are also your friend.
Q:: What is a weighted graph?
A:: A graph whose edges have a value.
This is useful in shortest path algorithms, like Dijkstra's algorithm.
Weighted graphs are really common in cyclic graphs
Q:: What is a cyclic graph?
A:: A graph which contains a cycle.
You can start at one node (vertex) and make your way back to that same node by following other nodes back to the node you started on.
Cyclic graphs are really common in weighted graphs
Q:: What is an acyclic graph?
A:: A graph that contains no cycles.
You cannot get back to a node you started from once you have left it.
Q:: What is an edge list?
A:: A collection of edges (connections) which represent a graph.
e.g.
// a third element can be inserted into each array to apply a weight graph e.g. [0, 2 ,88]
const graph = [
[0, 2],
[2, 3],
[2, 1],
[1, 3],
];Q:: What is an adjacent list?
A:: A collection of vertices and their neighboring vertices which represents a graph.
// The index is the node and the value is the nodes neighbors (we can use arrays, objects, linked lists)
// The index in this case is the value of the actual graph node
const graph = [
[2], // 0
[2, 3], // 1
[0, 1, 3], // 2
[1, 2], // 3
];Q:: What is an adjacent matrix?
A:: A graph representation by an array matrix which contain 0s and 1s that show the relationship of vertices to other vertices in the graph.
It will indicate if node X has a connection to node Y, 0 means NO, 1 means YES
If you have a weighted graph you can add weights here instead of 1 (is replaced by the weight) and 0
// The index in this case is the value of the actual graph node
// We can use an object to apply keys instead of indexes
const graph = [
[0, 0, 1, 0], // 0 -> 2
[0, 0, 1, 1], // 1 -> 2,3
[1, 1, 0, 1], // 2 -> 0,1,3
[0, 1, 1, 0], // 3 -> 1,2
];Q:: How would you create a graph structure?
A:: -
class Graph {
constructor() {
this.numberOfNodes = 0;
this.adjacentList = {};
}
addVertex(node) {
this.adjacentList[node] = [];
this.numberOfNodes++;
}
addEdge(node1, node2) {
//uniderected Graph
this.adjacentList[node1].push(node2);
this.adjacentList[node2].push(node1);
}
showConnections() {
const allNodes = Object.keys(this.adjacentList);
for (let node of allNodes) {
let nodeConnections = this.adjacentList[node];
let connections = "";
let vertex;
for (vertex of nodeConnections) {
connections += vertex + " ";
}
console.log(node + "-->" + connections);
}
}
}
var myGraph = new Graph();
myGraph.addVertex("0");
myGraph.addVertex("1");
myGraph.addVertex("2");
myGraph.addVertex("3");
myGraph.addVertex("4");
myGraph.addVertex("5");
myGraph.addVertex("6");
myGraph.addEdge("3", "1");
myGraph.addEdge("3", "4");
myGraph.addEdge("4", "2");
myGraph.addEdge("4", "5");
myGraph.addEdge("1", "2");
myGraph.addEdge("1", "0");
myGraph.addEdge("0", "2");
myGraph.addEdge("6", "5");
myGraph.showConnections();Q:: What are the pros of using graphs?
A:: 1. Relationships (some data needs to be in a graph form)
Q:: What are the cons of using graphs?
A:: 1. Scaling is hard (they can get complicated, you need a big company or at least a lot of resources and engineering power to make sure that you build graphs that scale well)
Q:: What is an algorithm?
A:: Steps to complete a desired action in computers. Technically all functions are algorithms.
Algorithms allow us to use data structures to perform actions on data
Data structures + Algorithms = Programs
Class {} + function() = Programs
Q:: What is recursion?
A:: When a function refers to itself (calls on itself). Think of inception (the movie).
It is good for tasks that have repeated subtasks to do
Q:: How do you terminate a recursive funtion?
A:: With a base case. Recursion breaks a task down into smaller tasks which terminate at the base case. This base case termination prevents the function from calling itself infinitely.
Q:: What are the 3 rules for recursion?
A:: 1. Identify the base case
2. Identify the recursive case
3. Return something in the base case and return your recursive calls so the value from the base case persists through the call stack
Q:: Write two functions that finds the factorial of any number. One should use recursive, the other should just use a for loop
function findFactorialRecursive(number) {
//code here
return answer;
}
function findFactorialIterative(number) {
//code here
return answer;
}A:: -
function findFactorialIterative(number) {
let answer = 1;
// you actually no longer need the if statement because of the for loop
// if (number === 2) {
// answer = 2;
// }
for (let i = 2; i <= number; i++) {
answer = answer * i;
}
return answer;
}
function findFactorialRecursive(number) {
if (number === 2) {
return 2;
}
return number * findFactorialRecursive(number - 1);
}
findFactorialIterative(5);
findFactorialRecursive(5);
//If you want, try to add a base case condition for the recursive solution if the parameter given is less than 2Q:: What does exponential time mean?
A:: It means that every additional element in a function we get an increase in function calls exponentially
e.g. (recursive algorithms that solves a problem of size N)
Q:: How can a recursive function be optimized?
A:: Dynamic programming and memoization!
Q:: Given a number N return the index value of the Fibonacci sequence, where the sequence is:
// 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ...
// the pattern of the sequence is that each value is the sum of the 2 previous values, that means that for N=5 → 2+3
//For example: fibonacciRecursive(6) should return 8
function fibonacciIterative(n) {
//code here;
}
fibonacciIterative(3);
function fibonacciRecursive(n) {
//code here;
}
fibonacciRecursive(3);A:: -
function fibonacciIterative(n) {
let arr = [0, 1];
for (let i = 2; i < n + 1; i++) {
arr.push(arr[i - 2] + arr[i - 1]);
}
return arr[n];
}
fibonacciIterative(3);
function fibonacciRecursive(n) {
if (n < 2) {
return n;
}
return fibonacciRecursive(n - 1) + fibonacciRecursive(n - 2);
}
fibonacciRecursive(6);Q:: What are the pros of using recursion?
A:: 1. DRY (simpler, have less loops happening with confusing code)
2. Readability (generally is more readable than an iterative aproach)
Q:: What are the cons of using recursion?
A:: 1. Large stack (it creates an extra memory footprint, because every time we add a function to the call stacks it adds extra piece of memory)
Q:: What is tail call optimization?
A:: There's something called tail call optimization in many languages And for example in Javascript with 6 it allows recursions to be called without increasing the call stack
There are certain ways to write recursion So there are more memory efficient.
Q:: When shall we use recursion?
A:: When it gets to complicated problems like traversing or searching through trees or graphs (DFS & BFS) recursion is really really useful and better than iterative aproaches
When we're sorting through items there's also cases that will see that recursion is preferred
e.g. (merge sort, quick sort)
Q:: What are the rules/factors to consider when deciding to write a recursive function?
A:: Every time you are using a tree or converting Something into a tree, consider recursion.
- Divided into a number of subproblems that are smaller instances of the same problem. e.g.(fibonacci / factorial problems)
- Each instance of the subproblem is identical in nature. (the calculations that we need to do are pretty much the same)
- The solutions of each subproblem can be combined to solve the problem at hand. (if you solve the smaller problems and you combine them that solves the problem at hand)
Divide and Conquer using Recursion
e.g. (looking through a phone book when you're looking for Bell in the phone book You're not going to start from a and simply go one page at a time from left to right. o you usually split the phonebook in the middle or try to go to the B section of the phone book and start dividing up the problem page by page until you get closer and closer)
Q:: Implement a function that reverses a string using iteration...and then recursion!
function reverseString(str) {}
reverseString("yoyo mastery");
//should return: 'yretsam oyoy'A:: -
function reverseString(str) {
let arrayStr = str.split("");
let reversedArray = [];
//We are using closure here so that we don't add the above variables to the global scope.
function addToArray(array) {
if (array.length > 0) {
reversedArray.push(array.pop());
addToArray(array);
}
return;
}
addToArray(arrayStr);
return reversedArray.join("");
}
reverseString("yoyo master");
function reverseStringRecursive(str) {
if (str === "") {
return "";
} else {
return reverseStringRecursive(str.substr(1)) + str.charAt(0);
}
}
reverseStringRecursive("yoyo master");Q:: Why should we review the documentation of the (native) methods we are using?
A:: To understand how it works in the language, it can also serve as a reference and a guide.
For example, in the case of javascript the implementation of the sort() method will vary depending on the environment where it is executed, ECMAScript says how it should look like (grab this argument and return this), but does not talk anything about the implementation.
Q:: What are the algorithms found in the "elementary sorts" category?
A:: Bubble sort, insertion sort, selection sort
They are, let's say, the first ones you would think of if you were told to implement some kind of order.
Q:: What is bubble sort?
A:: Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order. This algorithm is not suitable for large data sets as its average and worst-case time complexity is quite high.
Q:: What is the time and space complexity of Bubble Sort? (worst case)
A:: Time: O(n^2)
Space: O(1)
Q:: How would you implement bubble sort?
A:: -
const numbers = [99, 44, 6, 2, 1, 5, 63, 87, 283, 4, 0];
function bubbleSort(array) {
const length = array.length;
for (let i = 0; i < length; i++) {
for (let j = 0; j < length; j++) {
if (array[j] > array[j + 1]) {
//Swap the numbers
let temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
}
bubbleSort(numbers);
console.log(numbers);Q:: What is selection sort?
A:: Selection sort is a simple and efficient sorting algorithm that works by repeatedly selecting the smallest (or largest) element from the unsorted portion of the list and moving it to the sorted portion of the list (usually the beginning of an array).
Q:: What is the time and space complexity of Selection Sort? (worst case)
A:: Time: O(n^2)
Space: O(1)
Q:: How would you implement selection sort?
A:: -
const numbers = [99, 44, 6, 2, 1, 5, 63, 87, 283, 4, 0];
function selectionSort(array) {
const length = array.length;
for (let i = 0; i < length; i++) {
// set current index as minimum
let min = i;
let temp = array[i];
for (let j = i + 1; j < length; j++) {
if (array[j] < array[min]) {
//update minimum if current is lower that what we had previously
min = j;
}
}
array[i] = array[min];
array[min] = temp;
}
return array;
}
selectionSort(numbers);
console.log(numbers);Q:: What is insertion sort?
A:: Insertion sort is a simple sorting algorithm that works similar to the way you sort playing cards in your hands. The array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed at the correct position in the sorted part.
Q:: What is the time and space complexity for Insertion Sort? (worst case)
A:: Time: O(n^2)
Space: O(1)
Q:: How would you implement insertion sort?
A:: -
const numbers = [99, 44, 6, 2, 1, 5, 63, 87, 283, 4, 0];
function insertionSort(array) {
const length = array.length;
for (let i = 0; i < length; i++) {
if (array[i] < array[0]) {
//move number to the first position
array.unshift(array.splice(i, 1)[0]);
} else {
// only sort number smaller than number on the left of it. This is the part of insertion sort that makes it fast if the array is almost sorted.
if (array[i] < array[i - 1]) {
//find where number should go
for (var j = 1; j < i; j++) {
if (array[i] >= array[j - 1] && array[i] < array[j]) {
//move number to the right spot
array.splice(j, 0, array.splice(i, 1)[0]);
}
}
}
}
}
}
insertionSort(numbers);
console.log(numbers);Q:: What does Log Linear time mean?
A:: It means that:
- Has linear behavior nested in log steps
- Is bigger than O(n) but smaller than O(n^2)
e.g. usually sorting operations
Q:: What is merge sort?
A:: Merge sort is defined as a sorting algorithm that works by dividing an array into smaller subarrays, sorting each subarray, and then merging the sorted subarrays back together to form the final sorted array.
Q:: What technique do the merge sort and quick sort algorithms use?
A:: Divide & Conquer
Q:: What is the time and space complexity of Merge Sort? (worst case)
A:: Time: O(n log n)
Space: O(n)
Q:: What does it mean when a sorting algorithm is stable?
A:: If a sorting algorithm is stable then it will retain the original order of the data after sorting is completed.
If there are duplicates of data then the duplicate piece of data that was on the left will remain on the left and the right will remain to the right after sorting is done.
Q:: How would you implement merge sort?
A:: -
const numbers = [99, 44, 6, 2, 1, 5, 63, 87, 283, 4, 0];
function mergeSort(array) {
if (array.length === 1) {
return array;
}
// Split Array in into right and left
const length = array.length;
const middle = Math.floor(length / 2);
const left = array.slice(0, middle);
const right = array.slice(middle);
// console.log('left:', left);
// console.log('right:', right);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
const result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
// console.log(left, right)
return result.concat(left.slice(leftIndex)).concat(right.slice(rightIndex));
}
const answer = mergeSort(numbers);
console.log(answer);Q:: What is quick sort?
A:: QuickSort is a sorting algorithm based on the Divide and Conquer algorithm that picks an element as a pivot and partitions the given array around the picked pivot by placing the pivot in its correct position in the sorted array.
Q:: What is the time and space complexity of Quick Sort? (worst case)
A:: Time: O(n^2) # This can usually be avoided with a good 'pivot' point
Space: O(log(n))
Q:: How would you implement quick sort?
A:: -
const numbers = [99, 44, 6, 2, 1, 5, 63, 87, 283, 4, 0];
function quickSort(array, left, right) {
const len = array.length;
let pivot;
let partitionIndex;
if (left < right) {
pivot = right;
partitionIndex = partition(array, pivot, left, right);
//sort left and right
quickSort(array, left, partitionIndex - 1);
quickSort(array, partitionIndex + 1, right);
}
return array;
}
function partition(array, pivot, left, right) {
let pivotValue = array[pivot];
let partitionIndex = left;
for (let i = left; i < right; i++) {
if (array[i] < pivotValue) {
swap(array, i, partitionIndex);
partitionIndex++;
}
}
swap(array, right, partitionIndex);
return partitionIndex;
}
function swap(array, firstIndex, secondIndex) {
var temp = array[firstIndex];
array[firstIndex] = array[secondIndex];
array[secondIndex] = temp;
}
//Select first and last index as 2nd and 3rd parameters
quickSort(numbers, 0, numbers.length - 1);
console.log(numbers);Q:: When should you use insertion sort?
A:: Insertion sort is recommended when dealing with a small number of items or when the items are already mostly sorted. It is fast in such cases. Additionally, insertion sort requires minimal space and is easy to implement in code.
Q:: When should you use bubble sort and selection sort?
A:: To be honest you're never going to use bubble/selection sort. It's only really used for educational purposes as a way to teach sorting. But it's very rare that you'll find this in real life because is just not very efficient.
Q:: When should you use merge sort?
A:: The main reason is its efficient time complexity of O(n log(n)) in both best and worst case scenarios. If one is concerned about worst case scenarios, merge sort is a suitable choice.
However, if the goal is to sort data in memory and space complexity is a concern, merge sort can be costly because it requires O(n) space complexity. This means it uses a significant amount of memory.
On the other hand, if there are large files that cannot be sorted within memory limits, external sorting is required. In this case, merge sort becomes a good option because space complexity matters less. External sorting involves using a process outside of the main memory to sort the data.
In summary, merge sort is a favorable algorithm due to its efficient time complexity, making it suitable for worst case scenarios. However, if sorting in memory and space complexity is a concern, alternatives may be considered. For external sorting, such as with large files, merge sort is a good choice as space complexity becomes less significant.
Q:: When should you use quick sort?
A:: Quicksort is superior to merge sort in terms of average case time complexity and space complexity. It has comparable speed to merge sort, but with lower space requirements. Quicksort is considered one of the most popular sorting algorithms.
However, a drawback of Quicksort is its worst case scenario, where if the pivot is not chosen properly, the sorting process can become significantly slower. Therefore, it is important to exercise caution when using Quicksort, particularly if worst case scenarios are a concern. In such cases, it may be advisable to choose a different sorting algorithm.
Q:: When should you use heap sort?
A:: Heapsort is similar to quicksort and merge sort but has a space complexity of O(1), meaning it uses a constant amount of memory. However, in terms of average performance, heapsort is generally slower than quicksort in most cases.
Heapsort is recommended only when there is a significant concern about worst-case scenarios and memory usage. In most situations, the text suggests that quicksort or merge sort would be the preferred choices for sorting algorithms.
Q:: What is the time and space complexity of Heap Sort? (worst case)
A:: Time: O(n log n)
Space: O(1)
Q:: What are the most used comparison algorithms?
A:: Merge sort & Quick sort. they use divie and conquer to give us this O(n log (n)) performance boost
Q:: Can we beat O(n log (n)) when it comes to sorting?
A:: Mathematically it is impossible to improve on this . it's impossible because O(n log (n)) means that we have to sort by comparison, But there is one exception to this rule. you can beat O(n log (n)) with non-comparison sorts
Q:: What are the most commonly used non-comparison algorithms?
A:: Counting sort & Radix sort
Q:: How do the algorithms work without comparison?
A:: For non-comparison algorithms, the approach involves leveraging the binary representation of numbers and data stored in computers (zeros and ones) to facilitate sorting. By utilizing the inherent properties of binary representation, these algorithms can effectively organize and sort data.
Q:: On what type of data do non-comparison algorithms work?
A:: It only really works on numbers because of the way numbers are stored in memory.
Q:: Sort algorithm question
Which algorithm would you use for the following context?
Sort 10 schools around your house by distance
A:: Insertion sort
It's really fast on small sorts. It's easy to code and it has space complexity of of one. It also could be that these 10 schools are already presorted or nearly sorted on our list. So insertion is just the simplest for this type of small data.
Q:: Sort algorithm question
Which algorithm would you use for the following context?
eBay sorts listings by the current Bid amount
A:: Radix sort / Counting sort
I would actually use something like radix or counting sort because well a bid is usually a number between let's say $1 to let's say 50000. Probably even less. And because it's a fixed length of integers. Integers are most likely not going to be a hundred million because well hopefully nobody's bidding that much on eBay.
Q:: Sort algorithm question
Which algorithm would you use for the following context?
Sport scores on ESPN
A:: Quick sort
Sports scores on ESPN sports scores can vary. There's decimal places sometimes there's there's different formats such as tennis and soccer and different things and there's definitely lots of sports and lots of scores to handle. It's going to be the most efficient and although we might have the worst case I doubt that the scores are going to be sorted because there are just so many different kinds. But I'm also worried about in-memory sorting. So if I used merge sort it might be a little too much for this because of our increase space complexity
versus quicksort which if you remember has better space complexity.
Q:: Sort algorithm question
Which algorithm would you use for the following context?
Massive database (can't fit all into memory) needs to sort through past year's user data
A:: Merge sort
We can fill all this data into memory to sort it So we probably need to sort it out externally and let's say we need to sort through past years user data So it's a ton of data and we need to sort it somehow let's say by some sort of a date. What based on the information that I got here it sounds like I need to do something called merge sort And the reason I would pick this is because well it sounds that we're not gonna be storing really in memory because the data is so big but because the data is so big I'm really worried about the performance. I don't want the worst case of quicksort of O(n^2).
Q:: Sort algorithm question
Which algorithm would you use for the following context?
Almost sorted Udemy review data needs to update and add 2 new reviews
A:: Insertion sort
Although this data might be huge and maybe I have a lot of reviews. I'm assuming that most of the previous data is already sorted and all I'm doing is adding two new reviews to this data Insertion sort for pre ordered lists is going to work better than any other type of sorting.
Q:: Sort algorithm question
Which algorithm would you use for the following context?
Temperature Records for the past 50 years in Canada
A:: Radix sort / Counting sort / Quick sort
I would say that our First I would use something like radix or counting sort if the temperatures have no decimal places. If we're saying you know it's -30 to let's say 40 degrees that's a integer number between a small range that can workwell but if I want to sort through data that also has maybe temperatures that are really accurate and have decimal places which you cant do with radix or counting sort then I'm probably going to use quick sort again just so we can do some in memory sorting and hopefully save on that space complexity.
Q:: Sort algorithm question
Which algorithm would you use for the following context?
Large user name database needs to be sorted. Data is very random.
A:: Merge sort / Quick sort
I'm not really sure I don't have enough information to make a decision here. Maybe I would use merge sort if we have enough memory and memory isn't too expensive on the machine. Or maybe I'll use quicksort if I'm not too worried about worst case and that the user name databases isnt that large Maybe I'll just use quicksort just to save memory space
Q:: Sort algorithm question
Which algorithm would you use for the following context?
You want to teach sorting for the first time
A:: Bubble sort / Selection sort
Q:: What is linear/secuencial search?
A:: Linear Search is defined as a sequential search algorithm that starts at one end and goes through each element of a list until the desired element is found, otherwise the search continues till the end of the data set.
Q:: What is binary search?
A:: Binary Search is defined as a searching algorithm used in a sorted array by repeatedly dividing the search interval in half. The idea of binary search is to use the information that the array is sorted and reduce the time complexity to O(log N).
Q:: Which big O notation generally refers to the divide and conquer approach?
A:: O(log n)
Q:: What are traversals in a data structure?
A:: You can think of traversals as visiting every node O(n)
Q:: What is the big O of BFS and DFS?
A:: O(n)
BFS:
Time complexity is O(|V|), where |V| is the number of nodes. You need to traverse all nodes.
Space complexity is O(|V|) as well - since at worst case you need to hold all vertices in the queue.
DFS:
Time complexity is again O(|V|), you need to traverse all nodes.
Space complexity - depends on the implementation, a recursive implementation can have a O(h) space complexity [worst case], where h is the maximal depth of your tree.
Using an iterative solution with a stack is actually the same as BFS, just using a stack instead of a queue - so you get both O(|V|) time and space complexity.
(*) Note that the space complexity and time complexity is a bit different for a tree than for a general graphs becase you do not need to maintain a visited set for a tree, and |E| = O(|V|), so the |E| factor is actually redundant.
Q:: What is BFS?
A:: In this technique, each neighboring vertex is inserted into the queue if it is not visited. This is done by looking at the edges of the vertex. Each visited vertex is marked visited once we visit them hence, each vertex is visited exactly once, and all edges of each vertex are checked. So the complexity of BFS is V + E
Pseudocode for BFS:
create a queue Q
v.visited = true
Q.push(v)
while Q is non-empty
remove the head u of Q
mark and enqueue all (unvisited) neighbours of u
Since we are only iterating over the graph’s edges and vertices only once, hence the time complexity for both the algorithms is linear O(V+E).
Auxiliary Space Taken is O(V) at worst case.
Q:: What is DFS?
A:: While iterating with this technique, we move over each node and edge exactly once, and once we are over a node that has already been visited then we backtrack, which means we are pruning possibilities that have already been marked. So hence the overall complexity is reduced from exponential to linear.
Pseudocode for DFS:
DFS(Graph, vertex)
vertex.visited = true
for each v1 ∈ Graph.Adj[vertex]
if v1.visited == false
DFS(Graph, v1)
Q:: What are the pros of BFS?
A:: 1. Shortest path (It's very good for finding the shortest path between a starting point and any other reachable node because we always start off with the root node and then search the closest nodes first and then the nodes further)
2. Closer nodes (it will look at the closest node first)
Q:: What are the cons of BFS?
A:: 1. More memory (it uses more memory to keep track of the parents and the children nodes of that level)
Q:: What are the pros of DFS?
A:: 1. Less memory
2. Does path exist? (Does the path exist to us or not from a source know to a target note)
Q:: What are the cons of DFS?
A:: 1. Can get slow (The downside with depth first search is that it can get slow especially if the tree or graph is really really deep and it's not necessarily good at finding the shortest path.)
Q:: Search algorithm question
Which algorithm would you use for the following context? (BFS or DFS)
If you know a solution is not far from the root of the tree
A:: BFS
Q:: Search algorithm question
Which algorithm would you use for the following context? (BFS or DFS)
If the tree is very deep and solutions are rare
A:: BFS (DFS will take too long)
Q:: Search algorithm question
Which algorithm would you use for the following context? (BFS or DFS)
If the tree is very wide
A:: DFS (BFS will need to much memory)
Q:: Search algorithm question
Which algorithm would you use for the following context? (BFS or DFS)
If solutions are frequent but located deep in the tree
A:: DFS
Q:: Search algorithm question
Which algorithm would you use for the following context? (BFS or DFS)
Determining whether a path exists between two nodes
A:: DFS
Q:: Search algorithm question
Which algorithm would you use for the following context? (BFS or DFS)
Finding the shortest path
A:: BFS
Q:: What are the different ways in which we can implement DFS?
A:: 1. Inorder Traversal
2. Preorder Traversal
3. Postorder Traversal
Q:: What pseudocode or formula would you use to describe the inorder traversal (DFS)?
A:: Algorithm Inorder(tree)
1.Traverse the left subtree, i.e., call Inorder(left->subtree)
2.Visit the root.
3.Traverse the right subtree, i.e., call Inorder(right->subtree)
root=[33,101(r),105] (BT)
result=[33,101,105]
Q:: What pseudocode or formula would you use to describe the preorder traversal (DFS)?
A:: Algorithm Preorder(tree)
- Visit the root.
- Traverse the left subtree, i.e., call Preorder(left->subtree)
- Traverse the right subtree, i.e., call Preorder(right->subtree)
root=[33,101(r),105] (BT)
result=[101,33,105]
Q:: What pseudocode or formula would you use to describe the postorder traversal (DFS)?
A:: Algorithm Postorder(tree)
- Traverse the left subtree, i.e., call Postorder(left->subtree)
- Traverse the right subtree, i.e., call Postorder(right->subtree)
- Visit the root
root=[33,101(r),105] (BT)
result=[33,105,101]
Q:: What are the uses of inorder in DFS?
A:: Uses of Inorder Traversal:
In the case of binary search trees (BST), Inorder traversal gives nodes in non-decreasing order. To get nodes of BST in non-increasing order, a variation of Inorder traversal where Inorder traversal is reversed can be used.
Q:: What are the uses of preorder in DFS?
A:: Uses of Preorder:
Preorder traversal is used to create a copy of the tree. Preorder traversal is also used to get prefix expressions on an expression tree.
Q:: What are the uses of postorder in DFS?
A:: Uses of Postorder:
Postorder traversal is used to delete the tree. Please see the question for the deletion of a tree for details. Postorder traversal is also useful to get the postfix expression of an expression tree
Q:: How would you implement BFS and DFS (with its variations)?
A:: -
class Node {
constructor(value) {
this.left = null;
this.right = null;
this.value = value;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
insert(value) {
const newNode = new Node(value);
if (this.root === null) {
this.root = newNode;
} else {
let currentNode = this.root;
while (true) {
if (value < currentNode.value) {
//Left
if (!currentNode.left) {
currentNode.left = newNode;
return this;
}
currentNode = currentNode.left;
} else {
//Right
if (!currentNode.right) {
currentNode.right = newNode;
return this;
}
currentNode = currentNode.right;
}
}
}
}
lookup(value) {
if (!this.root) {
return false;
}
let currentNode = this.root;
while (currentNode) {
if (value < currentNode.value) {
currentNode = currentNode.left;
} else if (value > currentNode.value) {
currentNode = currentNode.right;
} else if (currentNode.value === value) {
return currentNode;
}
}
return null;
}
remove(value) {
if (!this.root) {
return false;
}
let currentNode = this.root;
let parentNode = null;
while (currentNode) {
if (value < currentNode.value) {
parentNode = currentNode;
currentNode = currentNode.left;
} else if (value > currentNode.value) {
parentNode = currentNode;
currentNode = currentNode.right;
} else if (currentNode.value === value) {
//We have a match, get to work!
//Option 1: No right child:
if (currentNode.right === null) {
if (parentNode === null) {
this.root = currentNode.left;
} else {
//if parent > current value, make current left child a child of parent
if (currentNode.value < parentNode.value) {
parentNode.left = currentNode.left;
//if parent < current value, make left child a right child of parent
} else if (currentNode.value > parentNode.value) {
parentNode.right = currentNode.left;
}
}
//Option 2: Right child which doesnt have a left child
} else if (currentNode.right.left === null) {
if (parentNode === null) {
this.root = currentNode.left;
} else {
currentNode.right.left = currentNode.left;
//if parent > current, make right child of the left the parent
if (currentNode.value < parentNode.value) {
parentNode.left = currentNode.right;
//if parent < current, make right child a right child of the parent
} else if (currentNode.value > parentNode.value) {
parentNode.right = currentNode.right;
}
}
//Option 3: Right child that has a left child
} else {
//find the Right child's left most child
let leftmost = currentNode.right.left;
let leftmostParent = currentNode.right;
while (leftmost.left !== null) {
leftmostParent = leftmost;
leftmost = leftmost.left;
}
//Parent's left subtree is now leftmost's right subtree
leftmostParent.left = leftmost.right;
leftmost.left = currentNode.left;
leftmost.right = currentNode.right;
if (parentNode === null) {
this.root = leftmost;
} else {
if (currentNode.value < parentNode.value) {
parentNode.left = leftmost;
} else if (currentNode.value > parentNode.value) {
parentNode.right = leftmost;
}
}
}
return true;
}
}
}
BreadthFirstSearch() {
let currentNode = this.root;
let list = [];
let queue = [];
queue.push(currentNode);
while (queue.length > 0) {
currentNode = queue.shift();
list.push(currentNode.value);
if (currentNode.left) {
queue.push(currentNode.left);
}
if (currentNode.right) {
queue.push(currentNode.right);
}
}
return list;
}
BreadthFirstSearchR(queue, list) {
if (!queue.length) {
return list;
}
const currentNode = queue.shift();
list.push(currentNode.value);
if (currentNode.left) {
queue.push(currentNode.left);
}
if (currentNode.right) {
queue.push(currentNode.right);
}
return this.BreadthFirstSearchR(queue, list);
}
DFTPreOrder(currentNode, list) {
return traversePreOrder(this.root, []);
}
DFTPostOrder() {
return traversePostOrder(this.root, []);
}
DFTInOrder() {
return traverseInOrder(this.root, []);
}
}
function traversePreOrder(node, list) {
list.push(node.value);
if (node.left) {
traversePreOrder(node.left, list);
}
if (node.right) {
traversePreOrder(node.right, list);
}
return list;
}
function traverseInOrder(node, list) {
if (node.left) {
traverseInOrder(node.left, list);
}
list.push(node.value);
if (node.right) {
traverseInOrder(node.right, list);
}
return list;
}
function traversePostOrder(node, list) {
if (node.left) {
traversePostOrder(node.left, list);
}
if (node.right) {
traversePostOrder(node.right, list);
}
list.push(node.value);
return list;
}
const tree = new BinarySearchTree();
tree.insert(9);
tree.insert(4);
tree.insert(6);
tree.insert(20);
tree.insert(170);
tree.insert(15);
tree.insert(1);
// tree.remove(170);
// JSON.stringify(traverse(tree.root))
console.log("BFS", tree.BreadthFirstSearch());
console.log("BFS", tree.BreadthFirstSearchR([tree.root], []));
console.log("DFSpre", tree.DFTPreOrder());
console.log("DFSin", tree.DFTInOrder());
console.log("DFSpost", tree.DFTPostOrder());
// 9
// 4 20
//1 6 15 170
function traverse(node) {
const tree = { value: node.value };
tree.left = node.left === null ? null : traverse(node.left);
tree.right = node.right === null ? null : traverse(node.right);
return tree;
}DECK INFO
TARGET DECK: Javascript::Interview::ADSA - Master the coding interview data structures algorithms - andrei neagoie
FILE TAGS: #Javascript #Interview
Reference:
Related:
LIST
where file.name = this.file.name