My review of the awesome SICP book.
Useful links:
- For Mac OS
-
-
brew install mit-scheme -
brew install rlwrap -
cp REPO/scheme-completion.txt ~/scheme-completion.txt -
echo 'alias sicp="rlwrap -r -c -f ~/scheme-completion.txt mit-scheme"' >> ~/.zshrc
-
If you are using Sublime Text, you can configure the build system:
{
"shell_cmd": "run-mit-scheme $file",
"file_regex": "^[ ]*File \"(...*?)\", line ([0-9]*)",
"selector": "source.scheme"
}I wrap mit-scheme program in run-mit-scheme script to append trailing new line so that the build result looks better in BuildX.
$ cat run-mit-scheme
#!/bin/bash
result=$(mit-scheme --quiet < $1)
code=$?
echo "$result"
exit $code- Setup
- Examples
- Chapter 1: Building Abstractions with Procedures
- Chapter 2: Building Abstractions with Data
- 2.1: Introduction to Data Abstraction
- 2.2: Hierarchical Data and the Closure Property
- Exercise 2.17
- Exercise 2.18
- Exercise 2.19
- Exercise 2.20
- Exercise 2.21
- Exercise 2.22
- Exercise 2.23
- Exercise 2.24
- Exercise 2.25
- Exercise 2.26
- Exercise 2.27
- Exercise 2.28
- Exercise 2.29
- Exercise 2.30
- Exercise 2.31
- Exercise 2.32
- Exercise 2.33
- Exercise 2.34
- Exercise 2.35
- Exercise 2.36
- Exercise 2.37
- Exercise 2.38
- Exercise 2.39
- Exercise 2.40
- Exercise 2.41
- Exercise 2.42
- Exercise 2.43
- Exercise 2.44
- Exercise 2.45
- Exercise 2.46
- Exercise 2.47
- Exercise 2.48
- Exercise 2.49
- Exercise 2.50
- Exercise 2.51
- Exercise 2.52
- 2.3: Symbolic Data
- 2.4: Multiple Representation for Abstract Data
|
Note
|
Due to the safety reasons, include:: directive in AsciiDoc will be transformed to link: in GitHub. So if you see something like link:test.js[] in the code block, you can manually go check the code in test.js.
|
Lisp is so old and also so good.
Lisp was invented in the late 1950s as a formalism for reasoning about the use of certain kinds of logical expressions, called recursion equations, as a model for computation. The language was conceived by John McCarthy and is based on his paper “Recursive Functions of Symbolic Expressions and Their Computation by Machine”.
Why SICP chooses lisp?
If Lisp is not a mainstream language, why are we using it as the framework for our discussion of programming? Because the language possesses unique features that make it an excellent medium for studying important programming constructs and data structures and for relating them to the linguistic features that support them.
One of the key features of every programming language is how to combine simple ideas to form more complex ideas.
Every powerful language has three mechanisms for accomplishing this:
primitive expressions, which represent the simplest entities the language is concerned with,
means of combination, by which compound elements are built from simpler ones, and
means of abstraction, by which compound elements can be named and manipulated as units.
Name matters.
A critical aspect of a programming language is the means it provides for using names to refer to computational objects.
Some expressions do not follow general evaluation rule. They are special so they are called special forms, like (define x 1).
Such exceptions to the general evaluation rule are called special forms. … Each special form has its own evaluation rule. The various kinds of expressions (each with its associated evaluation rule) constitute the syntax of the programming language.
Lisp has a very simple syntax.
In comparison with most other programming languages, Lisp has a very simple syntax; that is, the evaluation rule for expressions can be described by a simple general rule together with specialized rules for a small number of special forms.
Applicative order versus normal order.
This alternative “fully expand and then reduce” evaluation is known as normal-order evaluation , in contrast to the “evaluate the arguments and then apply” method that the interpreter actually uses, which is called applicative-order evaluation.
Lisp uses applicative-order evaluation.
Lisp uses applicative-order evaluation, partly because of the additional efficiency obtained from avoiding multiple evaluations of expres- sions … and, more significantly, because normal-order evaluation becomes much more complicated to deal with when we leave the realm of procedures that can be modeled by substitution. On the other hand, normal-order evaluation can be an extremely valuable tool.
-
10 ; 10 (+ 5 3 4) ; 12 (- 9 1) ; 8 (/ 6 2) ; 3 (+ (* 2 4) (- 4 6)) ; 6 (define a 3) ; a (define b (+ a 1)) ; b (+ a b (* a b)) ; 19 (= a b) ; #f (if (and (> b a) (< b (* a b))) b a) ; 4 (cond ((= a 4) 6) ((= b 4) (+ 6 7 a)) (else 25)) ; 16 (+ 2 (if (> b a) b a)) ; 6 (* (cond ((> a b) a) ((< a b) b) (else -1)) (+ a 1)) ; 16
-
We can clearly see the benefits of the syntax of Lisp. It’s so concise yet powerful.
link:chapter-1/1.1/1.02.scm[role=include]
-
(define (a-plus-abs-b a b) ((if (> b 0) + -) a b))
In this function, the operator itself is a subexpression
(if (> b 0) + -). It is either built-in procedure+or built-in procedure-based on the value ofb.In Lisp, operator and operands can be any complex expressions.
-
(define (p) (p)) (define (test x y) (if (= x 0) 0 y)) (test 0 (p))
In normal-order evaluator, the program would run normally, return 0. But in applicative-order evaluator, the program would hang forever.
Because in application-order evaluator, when it evaluates
(test 0 (p)), it will need to evaluate(p)first.pis a procedure which calls itself. So to evaluate(p), we get(p)again, and we evaluate that, we get it again, so on and so forth, we can never get a result.But in normal-order evaluator, it won’t evaluate operands until it has to. So
(test 0 (p))becomes(if (= 0 0) 0 (p). Because(= 0 0)is true, it will never evaluate(p).
How to compute square roots?
How does one compute square roots? Thee most common way is to use Newton’s method of successive approximations, which says that whenever we have a guess y for the value of the square root of a number x , we can perform a simple manipulation to get a better guess (one closer to the actual square root) by averaging y with x/y.
|
Note
|
MIT Scheme, however, distinguishes between exact integers and decimal values, and dividing two integers produces a rational number rather than a decimal. |
link:chapter-1/1.1/sqrt.scm[role=include]-
For small numbers, the result will be inaccurate. Let’s say we need to iterate 10 times to find the square root of number x, because x is very small, the first time iterated value and x can satisfy the
good-enough?condition.(display (sqrt 0.00001)) ; .03135649010771716 ; this value is very inaccurate
For big numbers, the program will run forever. We can never find a number to satisfy the condition because we only have limited precision.
; CAUTION! this function will run forever (display (sqrt 1.797693134862315708145274237317043567981e+308))
Does it help with the new
good-enough?implementation? Of course!link:chapter-1/1.1/1.07.scm[role=include]
-
link:chapter-1/1.1/1.08.scm[role=include]
We can define functions inside functions.
we allow a procedure to have internal definitions that are local to that procedure. Such nesting of definitions, called block structure, is basically the right solution to the simplest name-packaging problem.
What is lexical scoping?
Lexical scoping dictates that free variables in a procedure are taken to refer to bindings made by enclosing procedure definitions; that is, they are looked up in the environment in which the procedure was defined.
- Recursive process
-
(define (factorial n) (if (= n 1) 1 (* n (factorial (- n 1))))) (factorial 6) (* 6 (factorial 5)) (* 6 (* 5 (factorial 4))) (* 6 (* 5 (* 4 (factorial 3)))) (* 6 (* 5 (* 4 (* 3 (factorial 2))))) (* 6 (* 5 (* 4 (* 3 (* 2 (factorial 1)))))) (* 6 (* 5 (* 4 (* 3 (* 2 1))))) (* 6 (* 5 (* 4 (* 3 2)))) (* 6 (* 5 (* 4 6))) (* 6 (* 5 24)) (* 6 120) ; A linear recursion
This type of process, characterized by a chain of deferred operations, is called a recursive process. Carrying out this process requires that the interpreter keep track of the operations to be performed later on.
— page 44 - Iterative process
-
(define (factorial n) (define (fact-iter product counter max-count) (if (> counter max-count) product (fact-iter (* product counter) (+ counter 1) max-count))) (fact-iter 1 1 n)) (factorial 6) (fact-iter 1 1 6) (fact-iter 1 2 6) (fact-iter 2 3 6) (fact-iter 6 4 6) (fact-iter 24 5 6) (fact-iter 120 6 6) (fact-iter 720 7 6)
By contrast, the second process does not grow and shrink. At each step, all we need to keep track of, for any n, are the current values of the variables
product,counter, andmax-count. We call this an iterative process.— page 44
The essential feature of iterative process is that its state can be summarized by a fixed number of state variables.
In general, an iterative process is one whose state can be summarized by a fixed number of state variables, together with a fixed rule that describes how the state variables should be updated as the process moves from state to state and an (optional) end test that specifies conditions under which the process should terminate.
Pay attention that a recursive process is not the same as a recursive procedure. We can use a skill called Tail Call Optimization to get an iterative process of a recursive procedure.
In my understanding, process is the running entity and procedure is the static code.
When we describe a procedure as recursive, we are referring to the syntactic fact that the procedure definition refers (either directly or indirectly) to the procedure itself. But when we describe a process as following a pattern that is, say, linearly recursive, we are speaking about how the process evolves, not about the syntax of how a procedure is written.
-
(define (+ a b) (if (= a 0) b (inc (+ (dec a) b)))) (+ 4 5) (inc (+ 3 5)) (inc (inc (+ 2 5))) (inc (inc (inc (+ 1 5)))) (inc (inc (inc (inc (+ 0 5))))) (inc (inc (inc (inc 5)))) (inc (inc (inc 6))) (inc (inc 7)) (inc 8) 9 ; this is a recursive process.
(define (+ a b) (if (= a 0) b (+ (dec a) (inc b)))) (+ 4 5) (+ 3 6) (+ 2 7) (+ 1 8) (+ 0 9) 9 ; this is an iterative process.
-
link:chapter-1/1.2/1.10.scm[role=include]
How many different ways can we make change of $1.00, given half-dollars, quarters, dimes, nickels, and pennies?
This problem has a simple solution as a recursive procedure.
link:chapter-1/1.2/count-change.scm[role=include]It’s not obvious how to transform this to an iterative process. I managed to come up with one, but I have to say it’s not very straight forward.
link:chapter-1/1.2/count-change-iter.scm[role=include]-
The recursive version is very easy, just follow the formula.
Because this function is a slight modification of
fibonacci, we can use the same skill to construct the iterative function.link:chapter-1/1.2/1.11.scm[role=include]
-
It’s obvious that
f(row, index) = f(row-1, index-1) + f(row-1, index).link:chapter-1/1.2/1.12.scm[role=include]
-
Given
\[\begin{gathered} Fib(n) = Fib(n) + Fib(n-1) \\ \varphi = \frac{1 + \sqrt{5}}{2} \\ \psi = \frac{1 - \sqrt{5}}{2} \\ \end{gathered}\]If
\[\begin{gathered} Fib(n) = \frac{\varphi^n - \psi^n}{\sqrt{5}} \\ Fib(n-1) = \frac{\varphi^{n-1} - \psi^{n-1}}{\sqrt{5}} \\ \end{gathered}\]Because
\[\begin{align} \varphi\psi = -1 \\ \varphi + \psi = 1 \\ \end{align}\]We can get
\[\begin{align} \varphi^{n+1} - \psi^{n+1} & = \varphi\varphi^n - \psi\psi^{n} \\ & = (1 - \psi)\varphi^n - (1 - \varphi)\psi^n \\ & = \varphi^n - \psi\varphi^n - \psi^n + \varphi\psi^n \\ & = \varphi^n - \psi\varphi\varphi^{n-1} - \psi^n + \varphi\psi\psi^{n-1} \\ & = \varphi^n - \psi^n + \varphi^{n-1} - \psi^{n-1} \\ \\ Fib(n+1) & = Fib(n) + Fib(n-1) \\ & = \frac{\varphi^n - \psi^n + \varphi^{n-1} - \psi^{n-1}}{\sqrt{5}} \\ & = \frac{\varphi^{n+1} - \psi^{n+1}}{\sqrt{5}} \end{align}\]
Order of growth is a convenient way to express how many resources a process needs.
Let
nbe a parameter that measures the size of the problem, and letR(n)be the amount of resources the process requires for a problem of sizen.…
We say that
R(n)has order of growthΘ(f(n)), writtenR(n) = Θ(f(n))(pronounced “theta of f(n)”), if there are positive constantsk1andk2independent ofnsuch thatk1f(n) ≤ R(n) ≤ k2f(n)for any sufficiently largevalueofn.(In other words, for largen, the valueR(n)is sandwiched betweenk1f(n)andk2f(n).)
Order of growth provides only a rough idea.
Orders of growth provide only a crude description of the behavior of a process. For example, a process requiring n^2 steps and a process requiring 1000n^2 steps and a process requiring 3n^2 + 10n + 17 steps all have O(n^2) order of growth.
But it still can be very useful.
On the other hand, order of growth provides a useful indication of how we may expect the behavior of the process to change as we change the size of the problem.
-
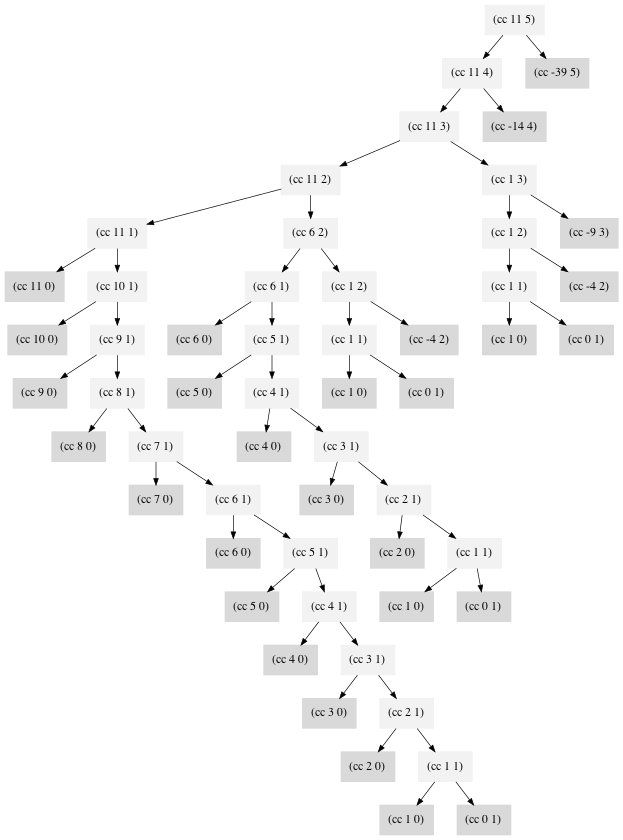
The image below is generated by chapter-1/1.2/1.14.py with Graphviz. Dark node is the leaf node.
The space complexity is the depth of the tree, and we can see that is
Θ(n).The time complexity is hard to analyze. The result is
cc(amount, kind) = Θ(amount^kind). Here is a detail explaination.
-
- a.
-
We need to get sine’s argument down to 0.1 by dividing 12.15 by 121.5 or greater number. Every time
pis applied, argument gets divided by 3. How many times we need to divide 12.15 by 3 to get down to 0.1? We need to find out the x from x^3 = 121.5.; x^3 = 121.5 ; x = log3(121.5) = log(121.5) / log(3) (display (/ (log 121.5) (log 3))) ; 4.37 ; So p will be applied 5 times.
- b.
-
Space and time complexity of
(sine a)are bothΘ(log3 a).
-
link:chapter-1/1.2/1.16.scm[role=include]
In general, the technique of defining an invariant quantity that remains unchanged from state to state is a powerful way to think about the design of iterative algorithms.
— page 60
-
p' = p^2 + q^2 q' = q^2 + 2pq Applying T(p,q) twice equals to applying T(p', q') once.
(define (gcd a b) (if (= b 0)
a
(gcd b (remainder a b))))Lamé’s Theorem: If Euclid’s Algorithm requires k steps to compute the GCD of some pair, then the smaller number in the pair must be greater than or equal to the kth Fibonacci number.
Based on Lamé’s Theorem, we can get an order-of-growth estimate for Euclid’s Algorithm.
Let n be the smaller of the two inputs to the procedure. If the process takes k steps, then we must have n ≥ Fib(k) ≈ φ^k/√5. Therefore the number of steps k grows as the logarithm (to the base φ) of n. Hence, the order of growth is Θ(log n).
-
Applicative order: (gcd 206,40) +1 -> (gcd 40, 6) +1 -> (gcd 6, 4) +1 -> (gcd 4, 2) +1 -> (gcd 2, 0) -> result 4 times. Normal order: (gcd 206 40) (gcd 40 (remainder 206 40)) +1 (gcd (remainder 206 40) (remainder 40 (remainder 206 40))) +2 (gcd (remainder 40 (remainder 206 40)) (remainder (remainder 206 40) (remainder 40 (remainder 206 40)))) +4 (gcd (remainder (remainder 206 40) (remainder 40 (remainder 206 40))) (remainder (remainder 40 (remainder 206 40)) (remainder (remainder 206 40) (remainder 40 (remainder 206 40))))) +7 (remainder (remainder 206 40) (remainder 40 (remainder 206 40))) +4 -> result 18 times!
link:chapter-1/1.2/prime.scm[role=include]This basic primality test is based on the fact that if n is not prime it must have a divisor less than or equal to √n. Consequently, the number of steps required to identify n as prime will have order of growth Θ(√n).
And there is a Θ(log n) test called the Fermat test which is based on a result from number theory known as Fermat’s Little Theorem.
Fermat’s Little Theorem: If n is a prime number and a is any positive integer less than n, then a raised to the nth power is congruent to a modulo n.
Given a number
n, pick a random numbera<nand compute the remainder ofa^nmodulon. If the result is not equal toa, thennis certainly not prime. If it isa, then chances are good thatnis prime. … By trying more and more values ofa, we can increase our confidence in the result. This algorithm is known as the Fermat test.
The core procedure of the Fermat test is one that computes the exponential of a number modulo another number.
link:chapter-1/1.2/fast-prime.scm[role=include]The Fermat test has a significant difference from most familiar algorithms, it is a probabilistic algorithm and the result is not guaranteed to be correct. But that doesn’t mean it is not useful.
The Fermat test differs in character from most familiar algorithms, in which one computes an answer that is guaranteed to be correct. Here, the answer obtained is only probably correct. More precisely, if n ever fails the Fermat test, we can be certain that n is not prime. But the fact that n passes the test, while an extremely strong indication, is still not a guarantee that n is prime. What we would like to say is that for any number n, if we perform the test enough times and find that n always passes the test, then the probability of error in our primality test can be made as small as we like.
Unfortunately, this assertion is not quite correct. There do exist numbers that fool the Fermat test: numbers n that are not prime and yet have the property that a^n is congruent to a modulo n for all integers a < n. Such numbers are extremely rare, so the Fermat test is quite reliable in practice.
There are variations of the Fermat test that cannot be fooled.
Numbers that fool the Fermat test are called Carmichael numbers, and little is known about them other than that they are extremely rare. There are 255 Carmichael numbers below 100,000,000. The smallest few are 561, 1105, 1729, 2465, 2821, and 6601.
-
(display (smallest-divisor 199)) (newline) ; 199 (display (smallest-divisor 1999)) (newline) ; 1999 (display (smallest-divisor 19999)) (newline) ; 7
-
-
Use
real-time-clockinstead ofruntimebecauseruntimereturns seconds which is too big to observe. -
Computers have become so fast, to get meaningful results, we need to test with very large numbers.
link:chapter-1/1.2/1.22.scm[role=include]
1000003.***2 1000033.***2 1000037.***2 10000019.***5 10000079.***5 10000103.***5 100000007.***16 100000037.***15 100000039.***14 1000000007.***44 1000000009.***44 1000000021.***44
We can see that the timing data basically corresponds to Θ(√n). The more bigger n gets, the better support for the Θ(√n) prediction.
-
-
chapter-1/1.2/1.23.scm is almost identical to 1.22.scm.
1000003.***1 1000033.***1 1000037.***1 10000019.***3 10000079.***3 10000103.***3 100000007.***10 100000037.***8 100000039.***8 1000000007.***24 1000000009.***25 1000000021.***24
We can see that the process runs basically twice as fast as exercise 1.22, so the expectation is confirmed.
-
-
1e10notation produces a float number, we need to usefloor→exactto convert it to an integer. Otherwiseremainderprocedure will error out. -
We need to use very large numbers to observe logarithmic growth.
link:chapter-1/1.2/1.24.scm[role=include]
100000000000000000039***14 100000000000000000129***12 100000000000000000151***12 10000000000000000303786028427003666890753***23 10000000000000000303786028427003666891041***23 10000000000000000303786028427003666891101***24 100000000000000000026609864708367276537402401181200809098131977453489758916313173***52 100000000000000000026609864708367276537402401181200809098131977453489758916313209***54 100000000000000000026609864708367276537402401181200809098131977453489758916313233***53
We can see that the running time of
1e80is roughly twice as1e40and four times as1e20, so our data supports the theory of logarithmic growth. -
-
In terms of the result, she is correct. We can get the exactly same result with
fast-expt.However, the computation process is largely different:
-
This method will produce a much larger intermediate result, which requires a lot of memory.
-
The large intermediate result requires the use of sepcial algorithm for multiplications and remainders which are much slower than computation on smaller values.
-
-
Because lisp using
applicative-orderevaluation,(remainder (* (expmod base (/ exp 2) m) (expmod base (/ exp 2) m)) m)needs to evaluate(expmod base (/ exp 2) m)twice.Thinking of the evaluation process, we get a tree of depth logN, at each level i, we have 2^i number of nodes.
Each node takes a constant time to calculate the result, so the overall time complexity corresponds to the total number of nodes which is Θ(log(2^n)) = Θ(N).
Procedures that manipulate procedures are called higher-order procedures.
-
- a
link:chapter-1/1.3/1.31-a.scm[role=include]
- b
link:chapter-1/1.3/1.31-b.scm[role=include]
-
- a
link:chapter-1/1.3/1.32-a.scm[role=include]
- b
link:chapter-1/1.3/1.32-b.scm[role=include]
-
link:chapter-1/1.3/1.33.scm[role=include]
In previous exercises, we can see that it’s terribly awkward to have to define trivial procedures using define. It would be more convenient to have a way to write these trivial procedures. Here comes the lambda special form!
In general, lambda is used to create procedures in the same way as define, except that no name is specified for the procedure:
(lambda (⟨formal-parameters⟩) ⟨body⟩)
The resulting procedure is just as much a procedure as one that is created using define. The only difference is that it has not been associated with any name in the environment.
We need a way to create local variables. Actually we can use lambda to do that.
(define (f x y)
((lambda (a b)
(+ (* x (square a))
(* y b)
(* a b)))
(+ 1 (* x y))
(- 1 y)))This construct is so useful that there is a special form called let to make its use more convenient. Using let, the f procedure could be written as
(define (f x y) (let a (+ 1 (* x y) (b (- 1 y))) (+ (* x (square a)) (* y b) (* a b))))
…
No new mechanism is required in the interpreter in order to provide local variables. A let expression is simply syntactic sugar for the underlying lambda application.
-
We will get an error: The object 2 is not applicable.
(f f) -> (f 2) -> (2 2) 2 is not a procedure.
We can use half-interval method to find roots of any equations.
The half-interval method is a simple but powerful technique for finding roots of an equation f (x) = 0, where f is a continuous function. The idea is that, if we are given points a and b such that f (a) < 0 < f (b), then f must have at least one zero between a and b.
link:chapter-1/1.3/half-interval.scm[role=include]What is a fixed-point?
A number x is called a fixed point of a function f if x satisfies the equa- tion f (x) = x. For some functions f we can locate a fixed point by beginning with an initial guess and applying f repeatedly,
f(x), f(f(x)), f(f(f(x))), …
until the value does not change very much.
Sometimes, fixed-point search does not converge. e.g. For function y = x/y, y1 = x/y0, y2 = y0. In these cases, we can use a method called average damping.
This approach of averaging successive approximations to a solution, a technique that we call average damping, often aids the convergence of fixed-point searches.
link:chapter-1/1.3/fixed-point.scm[role=include]-
Golden ratio φ satisfies the equation
x = 1 + 1/xso it’s the fixed point of functionf(x) = 1 + 1/x.link:chapter-1/1.3/1.35.scm[role=include]
-
link:chapter-1/1.3/1.36.scm[role=include]
-> 2. -> 9.965784284662087 -> 3.004472209841214 -> 6.279195757507157 -> 3.759850702401539 -> 5.215843784925895 -> 4.182207192401397 -> 4.8277650983445906 -> 4.387593384662677 -> 4.671250085763899 -> 4.481403616895052 -> 4.6053657460929 -> 4.5230849678718865 -> 4.577114682047341 -> 4.541382480151454 -> 4.564903245230833 -> 4.549372679303342 -> 4.559606491913287 -> 4.552853875788271 -> 4.557305529748263 -> 4.554369064436181 -> 4.556305311532999 -> 4.555028263573554 -> 4.555870396702851 -> 4.555315001192079 -> 4.5556812635433275 -> 4.555439715736846 -> 4.555599009998291 -> 4.555493957531389 -> 4.555563237292884 -> 4.555517548417651 -> 4.555547679306398 -> 4.555527808516254 -> 4.555540912917957 -> 2. -> 5.9828921423310435 -> 4.922168721308343 -> 4.628224318195455 -> 4.568346513136242 -> 4.5577305909237005 -> 4.555909809045131 -> 4.555599411610624 -> 4.5555465521473675
We can clearly see that average damping takes significantly less steps.
-
link:chapter-1/1.3/1.39.scm[role=include]
How to write a better procedure?
In general, there are many ways to formulate a process as a procedure. Experienced programmers know how to choose procedural formulations that are particularly perspicuous, and where useful elements of the pro- cess are exposed as separate entities that can be reused in other applications.
Newton’s method:
if g(x) is a differentiable function, then a solution of the equation g(x) = 0 is a fixed point of the function f(x) = x - g(x)/Dg(x), and Dg(x) is the derivative of g(x).
link:chapter-1/1.3/newtons-method.scm[role=include]We can use above procedure to calc square root:
link:chapter-1/1.3/sqrt-with-newtons-method.scm[role=include]To abstract or not to abstract?
As programmers, we should be alert to opportunities to identify the underlying abstractions in our programs and to build upon them and generalize them to create more powerful abstractions. This is not to say that one should always write programs in the most abstract way possible; expert programmers know how to choose the level of abstraction appropriate to their task.
What is a first-class element?
Some of the “rights and privileges” of first-class elements are:
They may be named by variables.
They may be passed as arguments to procedures.
They may be returned as the results of procedures.
They may be included in data structures.
-
link:chapter-1/1.3/1.45.scm[role=include]
Now we have a procedure to calculate nth roots of any numbers!
Complex world needs complex data.
Programs are typically designed to model complex phenomena, and more often than not one must construct computational objects that have several parts in order to model real-world phenomena that have several aspects. Thus, whereas our focus in chapter 1 was on building abstractions by combining procedures to form compound procedures, we turn in this chapter to another key aspect of any programming language: the means it provides for building abstractions by combining data objects to form compound data.
Why do we need compound data?
Why do we want compound data in a programming language? For the same reasons that we want compound procedures: to elevate the conceptual level at which we can design our programs, to increase the modularity of our designs, and to enhance the expressive power of our language.
What is the key to forming compound data?
We will see that the key to forming compound data is that a pro- gramming language should provide some kind of “glue” so that data objects can be combined to form more complex data objects.
The compound data user should know nothing about the compound data detail.
The basic idea of data abstraction is to structure the programs that are to use compound data objects so that they operate on “abstract data.” That is, our programs should use data in such a way as to make no assumptions about the data that are not strictly necessary for performing the task at hand.
-
link:chapter-2/2.1/2.01.scm[role=include]
Interface is the key.
Constraining the dependence on the representation to a few interface procedures helps us design programs as well as modify them, because it allows us to maintain the flexibility to consider alternate implementations.
-
link:chapter-2/2.1/2.02.scm[role=include]
(define s (make-segment (make-point 1.0 1.0) (make-point 10.0 10.0))) (print-point (midpoint-segment s)) ; (5.5,5.5)
-
link:chapter-2/2.1/2.03.scm[role=include]
What is data?
In general, we can think of data as defined by some collection of selectors and constructors, together with specified conditions that these procedures must fulfill in order to be a valid representation.
What is a pair? We know that we have cons, car and cdr as primitives and if we glue two objects using cons we can retrieve the objects using car and cdr.
Three procedures satisfying specified conditions give us a pair. And we can easily build it by ourself.
(define (cons x y)
(define (dispatch m)
(cond ((= m 0) x)
((= m 1) y)
(else (error "Argumetn not 0 or 1: " m))))
dispatch)
(define (car z) (z 0))
(define (cdr z) (z 1))The procedural representation, although obscure, is a perfectly adequate way to represent pairs, since it fulfills the only conditions that pairs need to fulfill.
-
(car (cons x y)) -> (car (lambda (m) (m x y))) -> ((lambda (m) (m x y)) (lambda (p q) p)) -> ((lambda (p q) p) x y) -> x (define (cdr z) (z (lambda (p q) q)))
-
This method can work not just with 2 and 3, but any relative prime numbers.
Let’s say p = (xa)(yb), x and y are relative prime. If we continually divide p with x, we can get zero remainder until x^a. p divides x^(a+1) must have a non-zero remainder.
link:chapter-2/2.1/2.05.scm[role=include]
-
This exercise requires a fair amount of understanding of Lambda Calcus.
Here is a fine material for Natural Numbers as Church Numerals.
If you are not interested in this topic, you can skip this exercise😉.
link:chapter-2/2.1/2.06.scm[role=include]
-
(define (lower-bound interval) (car interval)) (define (uppper-bound interval) (cdr interval))
-
For interval subtraction
x - y, the minimum value the difference could be is the lower bound of x subtracting the upper bound of y and the maximum value it could be is the upper bound of x subtracting the lower bound of y.(define (sub-interval x y) (make-interval (- (lower-bound x) (upper-bound y)) (- (upper-bound x) (lower-bound y))))
-
(define (div-interval x y) (if (and (<= (lower-bound y) 0) (>= (upper-bound y) 0)) (error "Can't divide a interval that spans 0") (mul-interval x (make-interval (/ 1.0 (upper-bound y)) (/ 1.0 (lower-bound y))))))
-
; p: 0 ~ 1 (define (make-center-percent c p) (define diff (* c p)) (make-interval (- c diff) (+ c diff))) (define (percent i) (/ (width i) (center i)))
-
Given
\[\begin{align} i_1 = [l_1, u_1] \\ i_2 = [l_2, u_2] \end{align}\]We can get
\[\begin{align} p_1 = \frac{u_1 - l_1}{u_1 + l_1} \\ p_2 = \frac{u_2 - l_2}{u_2 + l_2} \\ \end{align}\]Assume all numbers are positinve
\[i_3 = i_1i_2 = [l_1l_2, u_1u_2]\]So
\[p_3 = \frac{u_1u_2 - l_1l_2}{u_1u_2 + l_1l_2}\]Since
\[\begin{align} p_1 &= \frac{u_1 - l_1}{u_1 + l_1} \\ &= \frac{1 - \frac{l_1}{u_1}}{1 + \frac{l_1}{u_1}} \\ \end{align}\]We can get
\[\begin{align} \frac{l_1}{u_1} = \frac{1 - p_1}{1 + p_1} \\ \frac{l_2}{u_2} = \frac{1 - p_2}{1 + p_2} \end{align}\]So
\[\begin{align} p_3 &= \frac{u_1u_2 - l_1l_2}{u_1u_2 + l_1l_2} \\ &= \frac{1 - \frac{l_1}{u_1}\frac{l_2}{u_2}}{1 + \frac{l_1}{u_1}\frac{l_2}{u_2}} \\ &= \frac{1 - \frac{1 - p_1}{1 + p_1}\frac{1 - p_2}{1 + p_2}}{1 + \frac{1 - p_1}{1 + p_1}\frac{1 - p_2}{1 + p_2}} \\ &= \frac{p_1 + p_2}{1 + p_1p_2} \\ &\approx p_1 + p_2 \end{align}\]
-
Eva is right.
Based on the results from exercise 2.14, we can see that
par2produces a tighter interval thanpar1.TODO: Do the actual math to show that a formula will produce a tighter error bounds if it can be written in such a form that no variable that represents an uncertain number is repeated.
-
Because our interval arithmetic doesn’t have the concept of identity. I.e. A/A ≠ 1 ± 0%. This means that we can’t apply standard algebraic transformations to a formula and expect it to produce an interval with the same bounds afterwards.
In general we can state that the more interval-airthmetic operations we perform, the wider the results will be.
Can we devise an interval-arithmetic package that does not have this shortcoming? As the authors state, "This problem is very difficult". I am not a math guy and this is certainly beyond my scope.
Once we have the pair, we have everything.
As a consequence, pairs pro- vide a universal building block from which we can construct all sorts of data structures.
Do not confuse "closure" here with another common concept: closure usually means the implementation technique for representing procedures with free variables. But here the word "closure" means a totally different thing.
The ability to create pairs whose elements are pairs is the essence of list structure’s importance as a representational tool. We refer to this ability as the closure property of cons. In general, an operation for combining data objects satisfies the closure property if the results of combining things with that operation can themselves be combined using the same operation.
-
(define (square-list items) (if (null? items) nil (cons (square (car items)) (square-list (cdr items))))) (define (square-list items) (map square items))
-
The answer is reversed because the argument list is traversed in order, from first to last, but squares are added successively to the front of the answer list via
cons.The fix doesn’t work either because the arguments of
consis wrong.(cons value list)will not produce a new list. We can useappendto fix this problem.
-
Result printed by the interpreter:
(1 (2 (3 4)))The corresponding box-and-pointer structure and tree interpretation:
The image is borrowed from http://mngu2382.github.io/sicp/chapter2/01-exercise07.html.
-
; This is manageable (car (cdr (car (cdr (cdr '(1 3 (5 7) 9)))))) ; This is easy (car (car '((7)))) ; This is too complex (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr '(1 (2 (3 (4 (5 (6 7)))))))))))))))))) ; ''
-
(define x (list 1 2 3)) (define y (list 4 5 6)) (append x y) ; (1 2 3 4 5 6) (cons x y) ; ((1 2 3) 4 5 6) (list x y) ; ((1 2 3) (4 5 6))
-
link:chapter-2/2.2/2.32.scm[role=include]
Concentrate on the "signals":
The key to organizing programs so as to more clearly reflect the signal-flow structure is to concentrate on the “signals” that flow from one stage in the process to the next.
Why should we use sequence operations?
The value of expressing programs as sequence operations is that this helps us make program designs that are modular, that is, designs that are constructed by combining relatively independent pieces. We can encourage modular design by providing a library of standard components together with a conventional interface for connecting the components in flexible ways.
Modular construction is a powerful strategy for controlling com- plexity in engineering design.
-
Why this interchange makes the program run slowly?
It’s obvious that this interchange makes
queen-colsrun multiple times than before.We can get a rough idea that the new procedure needs approximately
T^7.TODO: The accurate timing analysis is hard, I am gonna leave it here.
-
link:chapter-2/2.2/2.52.scm[role=include]
The stratified design.
This is the approach of stratified design, the notion that a complex system should be structured as a sequence of levels that are described using a sequence of languages. Each level is constructed by combining parts that are regarded as primitive at that level, and the parts constructed at each level are used as primitives at the next level. The language used at each level of a stratified design has primitives, means of combination, and means of abstraction appropriate to that level of detail.
Lists containing symbols looks just like the expressions of our language, and that is homoiconic.
In order to manipulate symbols we need a new element in our language: the ability to quote a data object.
This issue is well known in the context of natural languages, where words and sentences may be regarded either as semantic entities or as character strings (syntactic entities).
For instance, If we tell somebody “say your name aloud,” we expect to hear that person’s name. However, if we tell somebody “say ‘your name’ aloud,” we expect to hear the words “your name.”
-
(car ''xxx)equals to(car (quote (quote xxx))), which equals to(car '(quote xxx)). So we getquoteback.
-
I have to admit, the time complexity analysis of recursive procedure is really hard.
TODO: detailed time complexity analysis.
link:chapter-2/2.3/2.63.scm[role=include]
-
link:chapter-2/2.3/2.66.scm[role=include]
Data abstraction is an essential help for designing a large system. And we can clearly see all the benefits from previous examples and exercises.
In designing such a system the methodology of data abstraction can be a great help.
The designer can create an initial implementation using a simple, straightforward representation such as unordered lists.
This will be unsuitable for the eventual system, but it can be useful in providing a “quick and dirty” data base with which to test the rest of the system.
Later on, the data representation can be modified to be more sophisticated.
If the data base is accessed in terms of abstract selectors and constructors, this change in representation will not require any changes to the rest of the system.
When we use a variable-length encoding, one of the difficulties is knowning when we have reached the end of a symbol in reading a sequence of zeros and ones.
We have two ways to solve this problem:
-
like Morse code, we can use a special separator code after the sequence for each letter.
-
We can design the code in such a way that no compelete code for any symbol is the prefix of the code for another symbol.
In general, we can attain significant savings if we use variable-length prefix codes that take advantage of the relative frequencies of the symbols in the messages to be encoded.
One particular scheme for doing this is called the Huffman encoding method, after its discoverer, David Huffman.
The algorithm for generating a Huffman tree is very simple. The idea is to arrange the tree so that the symbols with the lowest frequency appear farthest away from the root.
Begin with the set of leaf nodes, containing symbols and their frequencies, as determined by the initial data from which the code is to be constructed.
Now find two leaves with the lowest weights and merge them to produce a node that has these two nodes as its leaf and right branches.
The weight of the new node is the sum of the two weights.
Remove the two leaves from the original set and replace them by this new node. Now continue this process.
At each step, merge two nodes with the smallest weights, removing them from the set and replacing them with a node that has these two as its leaf and right branches.
The process stops when there is only one node left, which is the root of the entire tree.
Note, the algorithm does not always specify a unique tree, because there may not be unique smallest-weight nodes at each step. Also, the choice of the order in which the two nodes are merged (i.e., which will be the right branch and which will be the left branch) is arbitrary.
-
What is the order of growth in the number of steps needed to encode a symbol?
-
Search the symbol list at each node: O(n) time
-
Then take log_n branches (average case)
-
Total:
O(n * log_n)
Consider the relative frequencies of the n symbols are like what described in exercise 2.71.
Give the order of growth of the number of steps need to encode the most frequent and least frequent symbols in the alphabet.
For the most frequent symbol
-
Search through symbol list: O(n) time
-
Take the first single branch, since it will be at the top of the list: constant
-
Total:
O(n)
For the least frequent symbol
-
Search through symbol list at each level: O(n) time
-
Take the next branch, since we are only removing one node, it would be: O(n - 1)
-
Total:
O(n * (n - 1)) = O(n^2)
-
How to cope with data that may be represented in different ways?
This requires constructing generic procedures—procedures that can operate on data that may be represented in more than one way.
Our main technique for building generic procedures will be to work in terms of data objects that have type tags, that is, data objects that include explicit information about how they are to be processed.