Description: In a row of dominoes, tops[i] and bottoms[i] represent the top and bottom halves of the ith domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)
We may rotate the ith domino, so that tops[i] and bottoms[i] swap values.
Return the minimum number of rotations so that all the values in tops are the same, or all the values in bottoms are the same.
If it cannot be done, return -1.
Example:
Example 1:
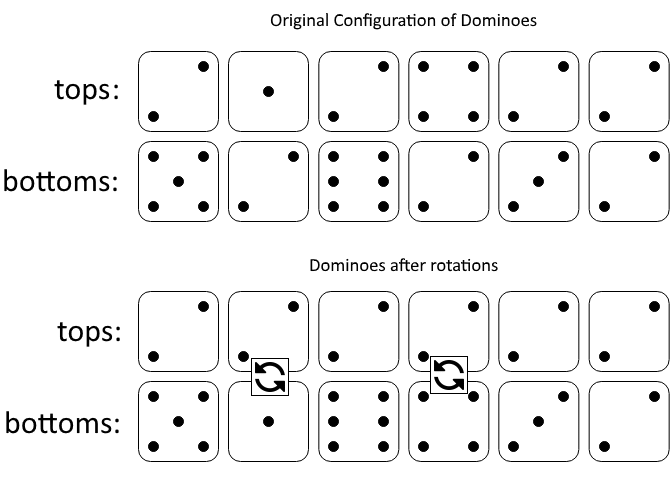
Input: tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2] Output: 2 Explanation: The first figure represents the dominoes as given by tops and bottoms: before we do any rotations. If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.
Example 2:
Input: tops = [3,5,1,2,3], bottoms = [3,6,3,3,4] Output: -1 Explanation: In this case, it is not possible to rotate the dominoes to make one row of values equal.
Constraints:
2 <= tops.length <= 2 * 10^4 bottoms.length == tops.length 1 <= tops[i], bottoms[i] <= 6
题目描述: 在一排多米诺骨牌中,A[i] 和 B[i] 分别代表第 i 个多米诺骨牌的上半部分和下半部分。(一个多米诺是两个从 1 到 6 的数字同列平铺形成的 —— 该平铺的每一半上都有一个数字。)
我们可以旋转第 i 张多米诺,使得 A[i] 和 B[i] 的值交换。
返回能使 A 中所有值或者 B 中所有值都相同的最小旋转次数。
如果无法做到,返回 -1.
示例 :
示例 1:
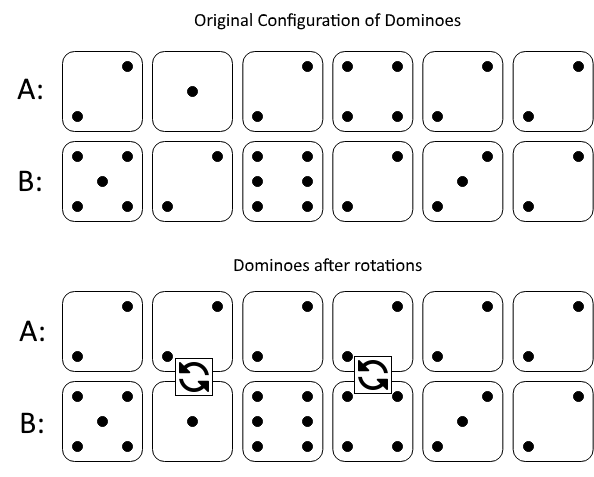
输入:A = [2,1,2,4,2,2], B = [5,2,6,2,3,2] 输出:2 解释: 图一表示:在我们旋转之前, A 和 B 给出的多米诺牌。 如果我们旋转第二个和第四个多米诺骨牌,我们可以使上面一行中的每个值都等于 2,如图二所示。
示例 2:
输入:A = [3,5,1,2,3], B = [3,6,3,3,4] 输出:-1 解释: 在这种情况下,不可能旋转多米诺牌使一行的值相等。
提示:
1 <= A[i], B[i] <= 6 2 <= A.length == B.length <= 20000
思路:
模拟 最多检查两次 以 tops[0] 或者 bottoms[0] 为基础查找交换 tops 或者 bottoms 的最小次数, 取较小的 时间复杂度为 O(n), 空间复杂度为 O(1)
代码: C++:
class Solution
{
public:
int minDominoRotations(vector<int>& tops, vector<int>& bottoms)
{
int n = tops.size(), r = helper(tops.front(), n, tops, bottoms);
if (r != -1 or tops.front() == bottoms.front()) return r;
else return helper(bottoms.front(), n, tops, bottoms);
}
private:
int helper(int x, int n, vector<int>& tops, vector<int>& bottoms)
{
int a = 0, b = 0;
for (int i = 0; i < n; i++)
{
if (tops[i] != x and bottoms[i] != x) return -1;
else if (tops[i] != x) ++a;
else if (bottoms[i] != x) ++b;
}
return min(a, b);
}
};Java:
class Solution {
public int minDominoRotations(int[] tops, int[] bottoms) {
int n = tops.length, r = helper(tops[0], n, tops, bottoms);
if (r != -1 || tops[0] == bottoms[0]) return r;
else return helper(bottoms[0], n, tops, bottoms);
}
private int helper(int x, int n, int[] tops, int[] bottoms) {
int a = 0, b = 0;
for (int i = 0; i < n; i++) {
if (tops[i] != x && bottoms[i] != x) return -1;
else if (tops[i] != x) ++a;
else if (bottoms[i] != x) ++b;
}
return Math.min(a, b);
}
}Python:
class Solution:
def minDominoRotations(self, tops: List[int], bottoms: List[int]) -> int:
n = len(tops)
def helper(x: int) -> int:
a = b = 0
for i in range(n):
if tops[i] != x and bottoms[i] != x:
return -1
elif tops[i] != x:
a += 1
elif bottoms[i] != x:
b += 1
return min(a, b)
if (r := helper(tops[0])) != -1 or tops[0] == bottoms[0]:
return r
else:
return helper(bottoms[0])