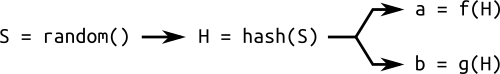Skip to content

Latest commit

 

History

History
 
 

ECC

Folders and files

NameName
Last commit message
Last commit date

parent directory

..
README.md
README.md
 
 
ecc_secp256k1.py
ecc_secp256k1.py
 
 
elliptic.py
elliptic.py
 
 
test.py
test.py
 
 
以太坊签名函数实操-elixir.md
以太坊签名函数实操-elixir.md
 
 

README.md

Elliptic Curve Cryptography

本文部分内容出自 Andrea Corbellini 的系列文章，搭配阅读原文体验更佳 Elliptic Curve Cryptography: a gentle introduction

椭圆曲线密码学（英语：Elliptic Curve Cryptography，缩写：ECC）是一种基于椭圆曲线数学的公开密钥加密算法。椭圆曲线在密码学中的使用是在 1985 年由 Neal Koblitz 和 Victor Miller 分别独立提出的。

ECC 的主要优势是它相比 RSA 加密算法使用较小的密钥长度并提供相当等级的安全性[1]。ECC 的另一个优势是可以定义群之间的双线性映射，基于 Weil 对或是 Tate 对。

比特币采用了椭圆曲线签名算法来签署交易。

建议预先掌握的知识点：

Elliptic Curves

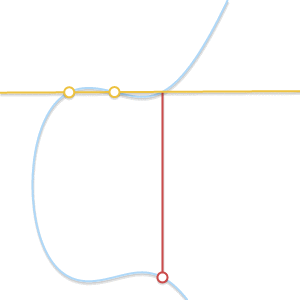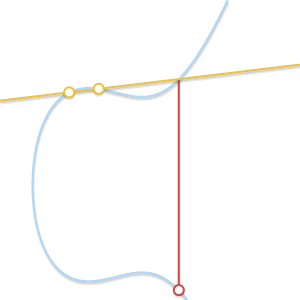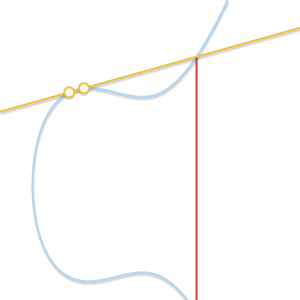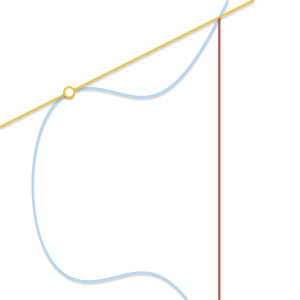
首先定义椭圆曲线方程，我们需要的是在曲线上的点的集合 (the set of points described by the equation)

Different shapes for different elliptic curves

Different shapes for different elliptic curves (b = 1, -3 < a < 2)

Types of singularities

Types of singularities: 左边是带奇点的曲线，右边是自相交的曲线，都不是有效的椭圆曲线

椭圆曲线关于 x 轴对称。我们还需要定义一个无穷远点作为 0 点 (symbol 0)

最终曲线定义如下

The group law for elliptic curves

Group

理解群的概念

群 G 是一个元素集合，我们给他定义了一个二元运算方法，“加法” +。

  1. closure: 对于 G 中的元素 a 和 b, a + b 也是 G 中的元素;
  2. associativity: (a+b)+c=a+(b+c);
  3. identity element: 单位元 0 ， a+0=0+a;
  4. inverse: 每个元素都有一个逆元，即对于 G 中的元素 a 都存在一个元素 b, a + b = 0;

我们附加了一条特性

  1. commutativity: a+b=b+a (Abelian group 阿贝尔群)

Geometric addition

我们在椭圆曲线上定义了一个群，是曲线上点的集合

  • 元素是椭圆曲线上的点
  • identity element 是无穷远的 0 点(point at infinity 0)
  • 对于点 P ，inverse (逆元) 是关于 x 轴对称的点
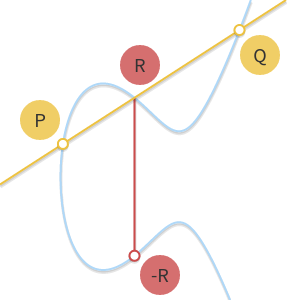
  • addition 加法的规则：一条直线与椭圆曲线相交的三个非 0 的点 P, Q, R 他们的和是 0 点，即 P+Q+R=0
    • P+Q=-R
    • -R 是 R 的逆元
    • 即 P+Q 等于 R 相对于 x 轴对称的点

Draw the line through and . The line intersects a third point . The point symmetric to it, , is the result of .

P+Q=-R

直线与椭圆曲线相交有三种特殊情况

  1. P=0 or Q=0. 我们不可能在 xy 坐标上标出 0 点(无穷远)，所以也无法画出这条线。但我们可以将 0 点定义为 identity element (单位元)，即 P+0=P and 0+Q=Q
  2. P=-Q. P 和 Q 关于 x 轴对称，此时直线将于 x 轴垂直，与椭圆曲线没有第三个交点 R，则 Q 是 P 的逆元，即 P+Q=0
  3. P=Q. Q 无限接近 P 点，直线是椭圆曲线的切线,P+Q=P+P=-R

As the two points become closer together, the line passing through them becomes tangent to the curve.

可以到这里尝试自己修改参数，观察曲线和直线交点的变化 HTML5/JavaScript visual tool

Algebraic addition

为了精确计算点的加法，我们需要把上述几何方法转换为代数算法。

已知 P,Q 的坐标，计算 R 点。

$$P=(xP, yP) Q=(xQ, yQ)$$

xP!=xQ

首先考虑 xP != xQ 的情况，直线的斜率 m 为

R 的坐标可以如下计算

或者

推导过程如下(感谢 kaiji 的补充)：

代入 Q 点和 P 点到椭圆曲线

将上述两个等式相减

将 yQ - yR 替换为 m(xQ-xR),等式两边消去 (yQ+yR)

同理可得

将上述两个等式相减

$m(y_P-y_Q)=(x_P+x_Q)(x_P-x_Q)+x_R(x_P-x_Q)$

两边同时除以 (xP-xQ)

$x_R=m^2-x_P-x_Q$

计算出 R 点之后，进而得出关于 x 轴对称点 -R，即为 P+Q 的结果

(xP,yP) + (xQ,yQ) = (xR,-yR)

我们可以用实际的点去验证上述公式

  • (1,2)+(3,4)=(-3,2)
  • (-1,4)+(1，2)=(1,-2)

xP=xQ

我们先将椭圆曲线方程改成 y 的一次方形式

当 P，Q 横坐标相同，直线为椭圆曲线的切线，我们将更改斜率 m 的定义为椭圆曲线的导函数

xR 和 yR 的公式保持不变，我们将 P=Q=(1,2) 代入公式验证

(1,2)+(1,2)=2(1,2)=(-1,-4)

Scalar multiplication

上述加法运算中，当 P=Q 时，P+P=2P，我们可以将其定义为 scalar multiplication 标量乘法。

nP=P+P+...+P (n times)

如果 n 在二进制中有 k 位(If n has k binary digits)，其算法复杂度 O(2^k)，我们需要对其优化。

double and add algorithm 用一个例子解释该算法工作原理：假设 n=151,其二进制表示为 10010111

double and add algorithm 将要做的是：

  • P, 即 2^0*P
  • P+P=2P, 即 2^1*P
  • 2P+2P=4P, 即 2^2*P
  • 4P+4P=8P, 即 2^3*P
  • 8P+8P=16P, 即 2^4*P
  • 151P = 2^4*P + 2^2*P + 2^1*P + 2^0*P

算法 python 实现

def bits(n):
    """
    Generates the binary digits of n, starting
    from the least significant bit.

    bits(151) -> 1, 1, 1, 0, 1, 0, 0, 1
    """
    while n:
        yield n & 1
        n >>= 1

def double_and_add(n, x):
    """
    Returns the result of n * x, computed using
    the double and add algorithm.
    """
    result = 0
    addend = x

    for bit in bits(n):
        if bit == 1:
            result += addend
        addend *= 2

    return result

假定 翻倍 doubling 和 加法 adding 操作都是 O(1), 那么这个算法将是 O(log(n)) (如果我们考虑 n 的位数，将是 O(k))

The field of integers modulo p

首先，有限域是具有有限个元素的集合。有限域的一个例子是模 p 的整数集合，其中 p 是素数。它通常表示为 Z/p、GF(p) 或 Fp。我们将使用后一种表示法。

在有限域中，我们有两种二元运算：addition(+), multiplication(·)。两种运算都符合 closed, associative and commutative 特性。

举例说明，对于 F23 (mod 23 的有限域)

  • Addition: (18+9) mod 23 = 4
  • Subtraction: (7-14) mod 23 = 16
  • Multiplication: 4·7 mod 23 = 5
  • Additive inverse: -5 mod 23 = 18
    • (5+(-5)) mod 23 = (5+18) mod 23 = 0
  • Multiplicative inverse: 9^-1 mod 23 = 18
    • 9·9^-1 mod 23 = 9·18 mod 23 = 1

p 必须是素数！

整数模 4 的集合不是一个域：2 没有乘法逆元（即方程 2⋅x mod 4=1 没有解）。

Division modulo p

在 Fp 中的除法模运算即为求出一个元素的乘法逆元，然后执行乘法运算。

x/y = x·y^-1

根据拓展欧几里得算法 extended Euclidean algorithm , 求出一个元素的乘法逆元的复杂度将是 O(log(p)) (如果考虑二进制位数将是 O(k))。

给定 n 和 p，求 n 在 Fp 中的乘法逆元，即当 n · n^-1 mod p = 1 时，求 n^-1

上述条件可以改写为 n · x - p · y = 1, 其中 y 为 n // p (商) ， x % p 即为 n^-1 (x 有可能比 p 大，固结果还要取模)

Computing the multiplicative inverse Python implementation

  • extended_euclidean_algorithm(a, b)
    • 根据拓展欧几里得算法，返回 GCD (最大公约数), x, y
    • 使用辗转相除法，当余数 r 为 0 时终止循环
    • 返回结果满足 a * x + b * y = GCD
  • inverse_of(n, p) 求 n 在 Fp 中的乘法逆元
    • 当 gcd = 1 时，乘法逆元即为 x % p
    • 否则 n 在 Fp 中不存在乘法逆元
def extended_euclidean_algorithm(a, b):
    """
    Returns a three-tuple (gcd, x, y) such that
    a * x + b * y == gcd, where gcd is the greatest
    common divisor of a and b.

    This function implements the extended Euclidean
    algorithm and runs in O(log b) in the worst case.
    """
    s, old_s = 0, 1
    t, old_t = 1, 0
    r, old_r = b, a

    while r != 0:
        quotient = old_r // r
        old_r, r = r, old_r - quotient * r
        old_s, s = s, old_s - quotient * s
        old_t, t = t, old_t - quotient * t

    return old_r, old_s, old_t


def inverse_of(n, p):
    """
    Returns the multiplicative inverse of
    n modulo p.

    This function returns an integer m such that
    (n * m) % p == 1.
    """
    gcd, x, y = extended_euclidean_algorithm(n, p)
    assert (n * x + p * y) % p == gcd

    if gcd != 1:
        # Either n is 0, or p is not a prime number.
        raise ValueError(
            '{} has no multiplicative inverse '
            'modulo {}'.format(n, p))
    else:
        return x % p

Elliptic curves in Fp

对椭圆曲线取模，公式将变成如下形式

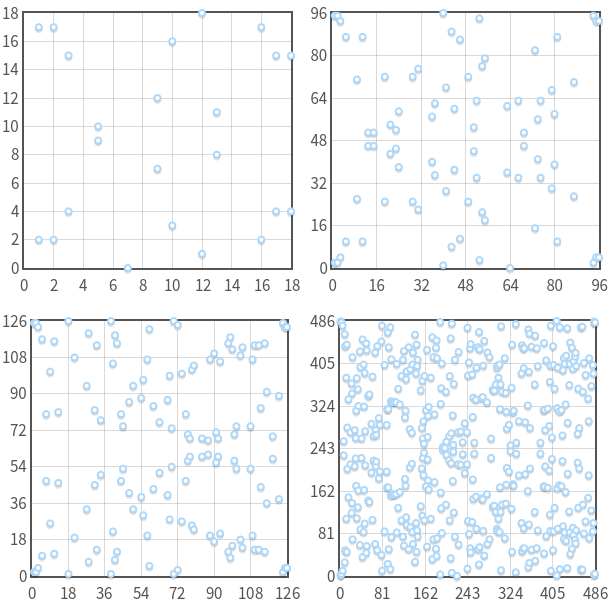
0 点仍然是无穷远点，(x, y) 是 Fp 中的整数。

(x,y) in Fp^2

(上图中 p = 19,97,127,487。可以对于每个 x 值，最多存在两个点，每个点关于 y=p/2 上下对称)

singular curve

(y^2= x^3 (mod 29)) 不是一个有效的椭圆曲线，包含了 0 点 (0,0)

在有限域 Fp 中，椭圆曲线仍然形成一个阿贝尔群。

Point addition

我们之前已经讨论过在椭圆曲线上 P+Q+R=0 的定义，三个点都在实属域 R 中。那么在有限域 Fp 中，将满足以下等式

addition in Fp

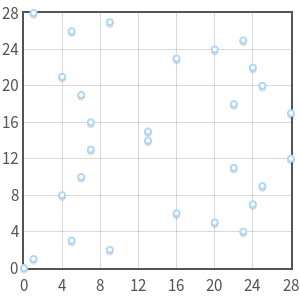
(curve y^2=x^3-x+3 (mod 127), P=(16,20) and Q=(41,120))

Fp 中的加法属性

  • Q + 0 = 0 + Q = Q (单位元的定义)
  • 给定非零点 Q，其逆元 -Q 是横坐标相同，但纵坐标关于 y=p/2 横线对称的点，即 -Q=(2, -5 mod 29) = (2, 24)
  • P+(-P)=0

Algebraic sum

将上述图形方法转为代数算法来计算 P+Q=-R

直接将实数域的公式增加 mod p

or

对于斜率 m，当 xP != xQ

当 xP = xQ

The order of an elliptic curve group

对于 Fp 的阶数 order (元素个数)，当 p 是一个很大的素数时，要计算 order 数量将会很困难， O(p)

Scalar multiplication and cyclic subgroups

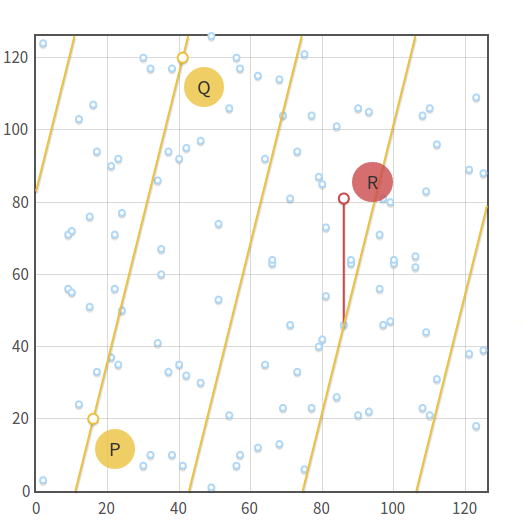
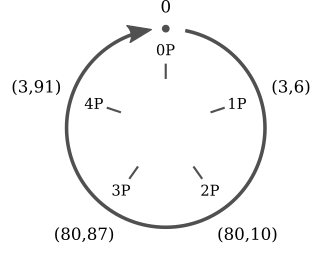
对于椭圆曲线 y^2=x^3+2x+3 (mod 97) 和点 P=(3,6)，P 只需要与自己相加 5 次即可回到初始点。

just five distinct points

  • 0P=0
  • 1P=(3,6)
  • 2P=(80,100)
  • 3P=(80,87)
  • 4P=(3,91)
  • 5P=0
  • ...

P 的倍数只有 5 个，且是循环出现的，于是我们可以重写一下结果：

  • 5kP=0
  • (5k+1)P=P
  • (5k+2)P=2P
  • (5k+3)P=3P
  • (5k+4)P=4P

P 的倍数组成的集合是椭圆曲线在 Fp 有限域中的循环子群。 (the set of the multiples of is a cyclic subgroup of the group formed by the elliptic curve.)

在该循环子群中，点 P 为称作生成元 或 基点 (generator or base point)。

循环子群是 ECC 和其他密码系统的基础。

Subgroup order

如何计算子群的阶数？

  • order 阶数即为群中元素的个数，对于上述循环子群，order of P 即为满足 nP=0 的最小正整数。
  • 根据拉格朗日定理 Lagrange's theorem， order of P 子群的阶数是父群的阶数的除数
    • 换言之，椭圆曲线包含 N 个点，其循环子群包含 n 个点，则 n 是 N 的除数

结合上述两条信息，计算子群阶数的步骤如下：

  1. 计算椭圆曲线包含的元素个数 N 使用 Schoof's algorithm
  2. 找出所有 N 的除数
  3. 对每个 N 的除数 n，计算 nP
  4. 满足 nP=0 条件的最小的正整数，即为子群的阶数 order of the subgroup

例 1：在 y^2=(x^3-x+3) mod 37 中，总的点个数 N = 42，可能的 order n=1,2,3,6,7,14,21,42. 给定点 P=（2,3）,我们可以尝试计算 P,2P,3P,6P,7P, 一直到 7P=0，因此由 P 点作为基点的循环子群，其阶数(order of P) n=7

例 2: 在 Y^2=(x^3-x+1) mod 29 中，总的点个数 N = 37。 由于 N 是素数，其除数只有 1 和 37。当子群的 order n = 1 时，其中只能包含一个元素，即无穷远 0 点。当 n = 37 时，子群就是整个曲线点集合。

Finding a base point

寻找基点(生成元)。

对于椭圆曲线加密算法，我们希望基点生成的子群拥有尽量多的个数，即 order 越大越好。因此我们会先算出椭圆曲线的点个数 N，然后选择其最大的除数作为子群的元素个数 n，再去匹配符合要求的基点。

令 h = N/n , 由于 n 是 N 的除数，固也是整数。我们称 h 为子群的辅因子 cofactor of the subgroup。

由于 nP=0 (循环子群的特性)， 而 N 是 n 的倍数，即 N = nh, 我们可得出

n(hP)=0

假设 n 是素数，用 G 表示所求的基点，则 G=hP。方法总结如下：

  1. 计算椭圆曲线的点个数 N
  2. 选择子群的阶数 n， 满足 n 是素数，且必须是 N 的除数
  3. 计算子群辅因子 cofactor h = N/n
  4. 在曲线上随机选择一个点 P
  5. 计算 G = hP
  6. 如果 G 是无穷远 0 点，返回第 4 步；不为 0 点，则我们找到了一个子群的基点(生成元)，其阶数为 n，辅因子为 h。

请注意，此算法仅在 n 是素数时才有效。如果 n 不是素数，则 G 的阶数可能是 n 的除数之一。

Discrete logarithm

在循环子群内，当我们已知 P 和 Q 点，要如何求 P=kQ 中的 k 是多少呢？将循环子群看成一个圆形时钟，从 P 到 Q，实际上我们无法得知究竟转了多少圈。这个逆运算的问题被称为离散对数问题 discrete logarithm problem。

discrete logarithm problem 被认为是很困难的，这一特性同样被运用在其他加密算法中，例如 RSA, D-H。

所不同的是，ECC 使用更少位数的 k 就能达到相同安全级别。

Domain parameters

我们的椭圆曲线算法将在有限域上的椭圆曲线的循环子群中工作。因此，我们的算法将需要以下参数

  • 素数 p 作为有限域的阶数.
  • 系数 a 和 b 定义椭圆曲线 (y^2 = x^3 + ax +b).
  • 循环子群的基点 G 作为生成元.
  • 循环子群的阶数 n.
  • 循环子群的辅因子 h.

Random curves

尽管椭圆曲线加密大部分是安全的，但仍有一些是比较弱的，会有安全隐患。如何才能保证一条椭圆曲线是安全的呢？

为了解决这个问题，我们使用种子 S 进行 hash 去生成系数 a, b, 或者基点 G，甚至全部用种子随机生成。

A simple sketch of how a random curve is generated from a seed

(A simple sketch of how a random curve is generated from a seed: the hash of a random number is used to calculate different parameters of the curve.)

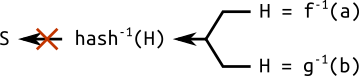
"hard" problem: hash inversion

(If we wanted to cheat and try to construct a seed from the domain parameters, we would have to solve a "hard" problem: hash inversion.)

参数由随机种子生成的曲线，称之为 verifiably random

Elliptic Curve Cryptography

定义公私钥对

  1. private key 是从 [1, n-1] (n 是子群的阶数) 中选取的整数 d
  2. public key 是点 H = dG (G 是子群的基点)

如果我们知道私钥 d 和 基点 G 找到公钥 H 0 是很容易的，但是反过来，已知 H 和 G，要找到私钥 d 是很困难的。

Encryption with ECDH

ECDH 是椭圆曲线 Diffie-Hellman 算法的变体。它实际上是一种密钥协商协议 key-agreement protocol，而不是一种加密算法。ECDH 定义了如何在各方之间生成和交换密钥。如何使用这些密钥实际加密数据取决于我们。

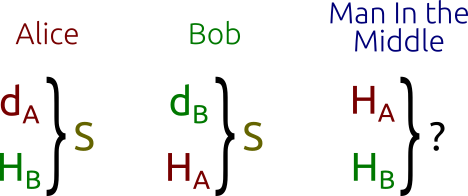
Alice 和 Bob 想要隐私且安全的交换信息，不被第三方看到内容：

  1. Alice 和 Bob 创建各自的公私钥对。Alice 的私钥 dA 公钥 HA = dA*G，Bob 的是 dB 和 HB = dB * G。 两人使用同一条曲线的同一个有限域（系数和生成元相同）
  2. Alice 和 Bob 互相交换公钥 HA 和 HB ，第三方可见公钥，但无法知道两人的私钥。
  3. Alice 计算出消息 S = dA*HB , Bob 也计算出消息 S = dB*HA， 两人会得到相同的结果

原理在于两人用自己的私钥乘以对方的公钥，其结果都是 dA*dB*G , 但第三方只知道公钥，就无法得到信息。

Diffie-Hellman key exchange

现在 Alice 和 Bob 已经获得了共享秘密 S ，他们可以通过对称加密交换数据。

ECDH demo

Ephemeral ECDH

ECDHE 中的“E”代表“Ephemeral”，指的是交换的密钥是临时的，而不是静态的。 例如，在 TLS 中使用 ECDHE，在建立连接时，客户端和服务器都会即时生成它们的公钥-私钥对。然后使用 TLS 证书对密钥进行签名（用于身份验证）并在各方之间进行交换。

Signing with ECDSA

ECDH 不能体现所有权，即 Alice 签名的消息，只有 Bob 可以验证，第三方无法验证真伪。

ECDSA 可以实现这一场景，它是 DSA Digital Signature Algorithm 的一种变体。

ECSDA 处理消息的 hash 而不是消息本身，hash 函数由我们自己选择。hash 会被截断，与 n (子群的阶数)的位数相同，截断后的 hash 应是一个整数，用 z 表示。

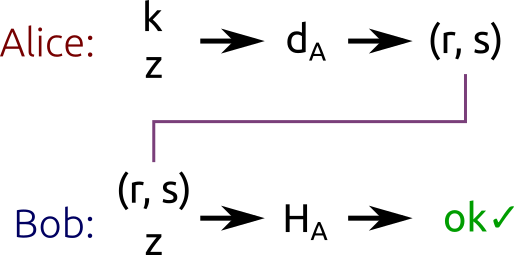
Alice 为消息签名所执行的算法如下：

  1. 从 [1, n-1] (n 是子群的阶数) 中选取随机的整数 k
  2. 计算点 P=kG (G 是子群的基点)
  3. 计算 r = xP mod n (xP 是 P 点横坐标)
  4. 如果 r 是 0，返回第 1 步
  5. 计算 s = k^-1(z + r*dA) mod n (dA 是 Alice 的私钥, k^-1 是 k 在 k mod n 中的乘法逆元)
  6. 如果 s 是 0，返回第 1 步

最终 (r, s) 对就是签名

ECDSA sign

Alice 使用她的私钥 dA 和随机 k 对哈希 z 进行签名。 Bob 使用 Alice 的公钥 HA 验证消息是否已正确签名。

再次强调，n 需要是素数，否则无法求 k^-1。

Verifying signatures

为了验证签名，我们需要 Alice 的公钥 HA、（截断的）hash z，还有签名 (r,s)。

  1. 计算整数 u1 = s^-1 * z mod n
  2. 计算整数 u2 = s^-1 * r mod n
  3. 计算点 P = u1*G + u2*HA

当 r == xP mod n 时，签名有效。

Correctness of the algorithm

算法的逻辑看起来不明显

P = u1*G + u2*HA

公钥的定义是 HA=dA*G (dA 是私钥)

$$P = u1*G + u2*HA = u1*G + u2*dA*G = (u1 + u2*dA)*G$$

再将u1 和u2 的定义代入

$$P = (u1 + u2*dA)*G = (s^-1*z + s^-1*r*dA)*G = s^-1(z + r*dA)*G$$

这里我们为了简洁省略了“mod n”，并且因为 G 生成的循环子群具有 n 阶，因此“mod n”是多余的。

之前我们定义了 s = k^-1(z + r*dA) mod n， 两边乘以 k 再除以 s 则

k = s^-1(z + r*dA) mod n

代入 P 的表达式

$$P = s^-1(z + r*dA)*G = k*G$$

这与签名时第2步相同，即如果 xP mod n 与 r 相同，则说明签名有效。

Playing with ECDSA

a Python script for signature generation and verification

The importance of k

在生成 ECDSA 签名时，将秘密 k 保密很重要。如果我们对所有签名使用相同的 k，或者如果我们的随机数生成器在某种程度上是可预测的，那么攻击者将能够找到私钥！

著名的 PlayStation 3 事故 This is the kind of mistake made by Sony a few years ago。索尼的ECDSA签名算法使用的时静态的 k，即每次的k值都相同，导致攻击者很容易就能破解私钥。

攻击者只需要购买两个游戏，然后提取他们的 hash (z1, z2) 和 签名 (r1,s1),(r2,s2)

  1. 首先 r1 = r2 ,因为 r = xP mod n , P = kG ,如果k值不变， r也不会变
  2. (s1 - s2) mod n = k^-1(z1 - z2) mod n
  3. 两边同时乘以 k ， k(s1 - s2) mod n = (z1 - z2) mod n
  4. k = (z1 - z2)(s1 - s2)^-1 mod n

最后通过k计算私钥 dS

s = k^-1 (z + r*dS) mod n

dS = r^-1 (s*k - z) mod n

其他 ECDSA 实现

mac m1 芯片可能无法安装 fastecdsa , 可以使用下列命令安装，详见 Cannot install in macOS BigSur (M1 chip)

CFLAGS=-I/opt/homebrew/opt/gmp/include LDFLAGS=-L/opt/homebrew/opt/gmp/lib python3 -m pip install --no-binary :all: --no-use-pep517 fastecdsa

参考