Skip to content

Latest commit

 

History

History
151 lines (100 loc) · 5.63 KB

README.md

File metadata and controls

151 lines (100 loc) · 5.63 KB
For a higher level encrypter, please check out my Vigenère Cipher software, which uses an advanced version of the Caesar Cipher.

Caesar Cipher

wakatime

About

To decrypt an encrypted Caesar Cipher string, most Caesar Cipher decrypters require the user to enter a key or use the bruteforce method (more on that later in this document). Using statistical models, this software automatically decrypts Caesar Ciphers without the use of a key.

History and usage

The Caesar Cipher was named after Julius Caesar (100 B.C. – 44 B.C). He would use the cipher for secret communication (protect messages of military significance). The Caesar Cipher is a substitution cipher. Originally, Julius Caesar would use a shift of three to encrypt/decrypt a message. The Caesar Cipher encrypts a message using an affine function : f(x) = 1x + b.

Detailed Explanations : How it works?

  1. Firstly, each character of the initial text (message to encrypt) is converted in a number from 0 to 25, corresponding to its position in the Latin alphabet which contains 26 letters --> (a = 0, b = 1 ... z = 25 ).

  2. Then, each number obtained is transformed by an affine function (f(x) = 1x + b). "x" is representing the number while "b" is defined during the encryption. "b" is the key used to decrypt the final message.

  3. If we take all the images and put them in a list, we obtain n numbers corresponding to n characters of the initial text. The next step consists in finding the values of modulo 26 of each number. (Modulo means remainder)

Example : Modulo 4 of 19 is 3 because 19 = 4 * 4 + 3 In the other hand, modulo 26 of 26 is 0 because 26 = 26 * 1 + 0

  1. Therefore, we obtain a new list with n element, each between 0 and 25 both included. All these numbers are converted in letters of the Latin Alphabet using the tables below.

  2. We finally create the final message by putting all the letters side by side.

Steps 1 and 4 can be done with these tables :

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

Weaknesses

  • If an attacker knows that the message has been encrypted using Caesar Cipher, he/she can try all shifts (b values from 1 to 25) to decrypt the message. This is called the bruteforce method.

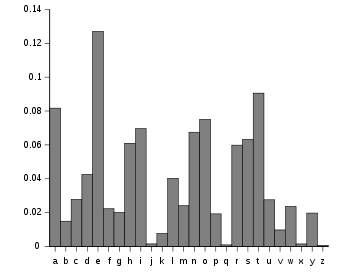
  • We can also use frequency analysis to decrypt the message as each letter is encrypted with the same algorithm and the most common letters in english are :

Example

Encrypting

  • Message to encrypt : ZATTACKZ
  • Shift used : 4 (f(x) = 1x + 4)
  • That means that b = 4

Using the above tables, ATTACK can be written as : 25 0 19 19 0 2 10 25 Images of each number :

  • f(25) = 29
  • f(0) = 4
  • f(19) = 23
  • f(2) = 6
  • f(10) = 14

The new list is : 29 4 23 23 4 6 14 29

Using the modulo 26 method, we obtain:

  • Mod(29,26) = 3
  • Mod(4,26) = 4
  • Mod(23,26) = 23
  • Mod(6,26) = 6
  • Mod(14,26) = 14

The final message is 3 4 23 23 4 6 14 3 and using the tables again, we convert them in the encrypted message :

DEXXEGOD

ZATTACKZ is encrypted with the function x + 4 and becomes DEXXEGOD.

Decrypting

First method : Knowing the key (value of the shift used)

  • Message to decrypt : DEXXEGOD
  • Shift used : 4 (f(x) = 1x - 4)
  • That means that b = -4

Using the above tables, DEXXEGOD can be written as : 3 4 23 23 4 6 14 3 Images of each number :

  • f(3) = -1
  • f(4) = 0
  • f(23) = 19
  • f(6) = 2
  • f(14) = 10

The new list is : -1 0 19 19 0 2 10 -1

Using the modulo 26 method, we obtain :

  • Mod(-1,26) = 25
  • Mod(0,26) = 0
  • Mod(19,26) = 19
  • Mod(2,26) = 2
  • Mod(10,26) = 10

The final message is 25 0 19 19 0 2 10 25 and using the tables again, we convert them in the encrypted message :

ZATTACKZ

DEXXEGOD is decrypted with the function 1x - 4 and becomes ZATTACKZ.

Second method : Not knowing the key (value of the shift used)

This is called the bruteforce method.

  • Message to decrypt : DEXXEGOD

Using the above tables, DEXXEGOD can be written as : 3 4 23 23 4 6 14 3

a is a number between 0 and 25. (a = 0 would mean the message is already decrypted)

Using the function f(x) = Mod(1x + a, 26) :

We can get all these results :

a Decrypted text
1 fgzzgiqf
2 ghaahjrg
3 hibbiksh
4 ijccjlti
5 jkddkmuj
6 kleelnvk
7 lmffmowl
8 mnggnpxm
9 nohhoqyn
10 opiiprzo
11 pqjjqsap
12 qrkkrtbq
13 rsllsucr
14 stmmtvds
15 tunnuwet
16 uvoovxfu
17 vwppwygv
18 wxqqxzhw
19 xyrryaix
20 yzsszbjy
21 zattackz
22 abuubdla
23 bcvvcemb
24 cdwwdfnc
25 dexxegod

The only text that makes sense is zattackz so we can deduce that the key is 21 (25 - b = 21).

DEXXEGOD is decrypted with the function f(x) = 1x - 4 or f(x) = 1x + 21 and becomes ZATTACKZ.