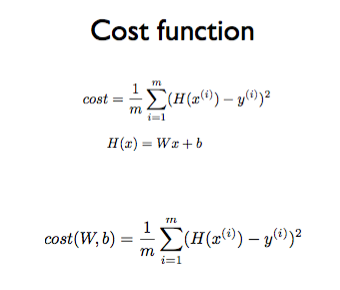점들이 퍼져있는 형태에서 패턴을 찾아내고, 이 패턴을 활용해서 무언가를 예측하는 분석.
새로운 표본을 뽑았을 때 이 표본이 평균으로 돌아가려는 특징이 있기 때문에 붙은 이름이다. 회귀(回歸 돌 회, 돌아갈 귀)라는 용어는 일반적으로 '돌아간다'는 뜻인데, 새로운 데이터 표본이 평균으로 돌아가려는 특성이 있다는 뜻에서 붙여진 이름이다. 하지만 이 특성으로 예측을 하고 싶은 것이지 이 '돌아가려는 특성' 을 분석하는것이 주는 아니다.
따라서 기존의 데이터(점)가 퍼져있는 형태의 패턴을 기반으로, 새로운 데이터에 대해 예측하는 것이라고 생각할수 있다.
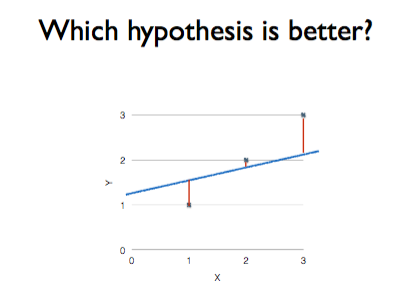
어떠한 직선이 우리 데이터 모델에 더 잘 맞는 직선인가?
회귀분석의 특성을 기반으로 2차원 좌표에 분포된 데이터를 1차원 직선 방정식을 통해, 아직 표현되지 않은 데이터를 예측하기 위한 분석 모델.
Linear Regression에서 사용하는 1차원 방정식을 가리키는 용어로, 우리말로는 가설이라고 한다. 수식에서는 h(x) 또는 H(x)로 표현한다.
H(x) = Wx + b 에서 Wx + b는 x에 대한 1차 방적식으로 직선을 표현. 기울기에 해당하는 W(Weight)와 절편에 해당하는 b(bias)가 가장 적절한 값이 나올 때 까지 계속 바뀌고, 마지막 루프에서 바뀐 최종 값을 사용해서 데이터 예측(prediction)에 사용하게 된다.
최종 결과로 나온 가설을 모델(model) 이라고 부르고, "학습되었다"라고 한다. 학습된 모델은 배포되어서 새로운 학습을 통해 수정되기 전까지 지속적으로 활용된다.
아래의 그림과 같이, 가설 직선 H(x) 과 실제 데이터 사이의 거리가 가까울수록 좋은 가설이 될 수 있다. 따라서 더 좋은 가설이 될 직선을 찾기 위해 계속해서 W와 b의 값을 수정하는 것이다.
H(x) 방정식과 실제 데이터 사이의 거리. 이를 계산하는 것이 Cost 함수(Loss function) 이다.
Cost함수는 위의 사진과 같이 다수의 점으로 이루어진 각 데이터와 가장 가까운 H(x)와의 거리를 각각 재서 그 거리의 평균을 내는 것이다. 식은 다음과 같다.
H(x)-y 에 제곱을 해주는 이유는 두 수의 차가 양수가 될 수도, 음수가 될 수도 있기 때문에 처음부터 양수로 바꿔주기 위함이다. 또한 제곱을 함으로써 H(x)와 y의 갭이 클 때 더 쉽게 패널티를 줄 수 있다.
이 예측의 정확도는 minimize 될 수록 정확하다. 이러한 점이 선형회귀 학습의 목표가 된다.