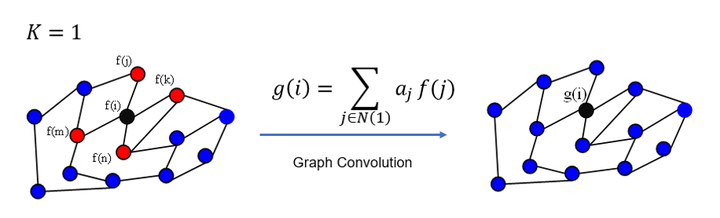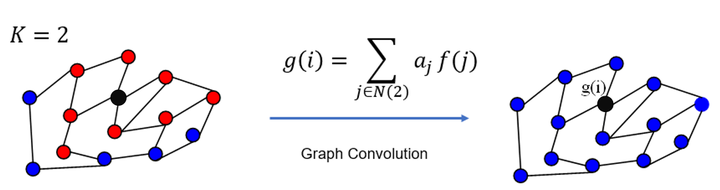- https://www.zhihu.com/question/54504471
- https://en.wikipedia.org/wiki/Laplacian_matrix
- https://tkipf.github.io/graph-convolutional-networks/
- https://www.inference.vc/how-powerful-are-graph-convolutions-review-of-kipf-welling-2016-2/
- http://cs229.stanford.edu/section/cs229-moregaussians.pdf
- Spatio-Temporal Graph Convolutional Network
- tackle the time series prediction problem in traffic domain
- complete convolutional structures.
- linear regression perform well on short interval forecast instead of long terms
- this is a data-driven and using spotio-temporal information method.
- fully utilize spatio-information instead of treating it as discrete units
$$\hat v_{t+1},...,\hat v_{t+H} = argmax log_{10} P(v_{t+1},...,v_{t+H}|v_{t-M},...,v_{t})$$ 
- where
$$v_t \in R^n$$ , n is an observation vector of n road segments at time step t
-
normalized Laplacian
-
- if k == n, receptive field is n hop