-
-
Notifications
You must be signed in to change notification settings - Fork 209
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Cannot beat OpenModelica score with ModelingToolkit.jl and OrdinaryDiffEq.jl #1693
Comments
|
Hi @LiborKudela ! Are you solving to the same tolerances with both MTK and modelica? |
|
|
Share |
|
[6e4b80f9] BenchmarkTools v1.3.1 |
|
Modelica defaults to KLU. I just did a bunch of tests and it makes sense for us too, so I changed the default linear solver. UMFPACK is rarely better. As for the compilation time, this is a known issue with MTK that is being worked on. |
|
Hey, could you run the above benchmark again using the latest MTK? It should be able to handle larger systems now. |
|
Hi, I will run it later today. Thank you! |
|
@YingboMa, I have run the benchmark. First I have updated everything. Julia version: ]st : I have also changed the symbolic arrays from I am unable to run Should I change something more in the script to take advantage of the new version of MTK? The script I used for this test: using ModelingToolkit, OrdinaryDiffEq, Symbolics, IfElse, XSteam,
Polynomials, Plots, LinearSolve
# o o o o o o o < heat capacitors
# | | | | | | | < heat conductors
# o o o o o o o
# | | | | | | |
#Source -> o--o--o--o--o--o--o -> Sink
# advection diff source PDE
@variables t
D = Differential(t)
m_flow_source(t) = 2.75
T_source(t) = (t>12*3600)*56.0 + 12.0
@register_symbolic m_flow_source(t)
@register_symbolic T_source(t)
#build polynomial liquid-water property only dependent on Temperature
p_l = 5 #bar
T_vec = collect(1:1:150);
kin_visc_T = fit(T_vec, my_pT.(p_l, T_vec)./rho_pT.(p_l, T_vec), 5);
lambda_T = fit(T_vec, tc_pT.(p_l, T_vec), 3);
Pr_T = fit(T_vec, 1e3*Cp_pT.(p_l, T_vec).*my_pT.(p_l, T_vec)./tc_pT.(p_l, T_vec), 5);
rho_T = fit(T_vec, rho_pT.(p_l, T_vec), 4);
rhocp_T = fit(T_vec, 1000*rho_pT.(p_l, T_vec).*Cp_pT.(p_l, T_vec), 5);
@connector function FluidPort(;name, p=101325.0, m=0.0, T=0.0)
sts = @variables p(t)=p m(t)=m [connect=Flow] T(t)=T [connect=Stream]
ODESystem(Equation[], t, sts, []; name=name)
end
@connector function VectorHeatPort(;name, N=100, T0=0.0, Q0=0.0)
#TODO: Vector of flow vars warning but eqs are correct!!
sts = @variables (T(t))[1:N]=T0 (Q(t))[1:N]=Q0 [connect=Flow]
ODESystem(Equation[], t, [T; Q], []; name=name)
end
#Taylor-aris dispersion model
function Dxx_coeff(u, d, T)
Re = abs(u)*d/kin_visc_T(T) + 0.1
IfElse.ifelse(Re < 1000, (d^2/4)*u^2/48/0.14e-6, d*u*(1.17e9*Re^(-2.5) + 0.41))
end
#Nusselt number model
function Nusselt(Re, Pr, f)
IfElse.ifelse(Re <= 2300, 3.66,
IfElse.ifelse(Re <= 3100, 3.5239*(Re/1000)^4-45.158*(Re/1000)^3+212.13*(Re/1000)^2-427.45*(Re/1000)+316.08,
f/8*((Re-1000)*Pr)/(1+12.7*(f/8)^(1/2)*(Pr^(2/3)-1))))
end
#Darcy weisbach friction factor
function Churchill_f(Re, epsilon, d)
theta_1 = (-2.457*log(((7/Re)^0.9)+(0.27*(epsilon/d))))^16
theta_2 = (37530/Re)^16
8*((((8/Re)^12)+(1/((theta_1+theta_2)^1.5)))^(1/12))
end
function FluidRegion(;name, L=1.0, dn=0.05, N=100, T0=0.0,
lumped_T=50, diffusion=true, e=1e-4)
@named inlet = FluidPort()
@named outlet = FluidPort()
@named heatport = VectorHeatPort(N=N)
dx=L/N
c=[-1/8, -3/8, -3/8] # advection stencil coeficients
A = pi*dn^2/4
p = @parameters C_shift = 0.0 Rw = 0.0 # stuff for latter
@variables begin
(T(t))[1:N] = fill(T0, N)
Twall(t)[1:N] = fill(T0, N)
(S(t))[1:N] = fill(T0, N)
(C(t))[1:N] = fill(1.0, N)
u(t) = 1e-6
Re(t) = 1000.0
Dxx(t) = 0.0
Pr(t) = 1.0
alpha(t) = 1.0
f(t) = 1.0
end
sts = [T..., Twall..., S..., C..., u, Re, Dxx, Pr, alpha, f]
eqs = [
Re ~ 0.1 + dn*abs(u)/kin_visc_T(lumped_T)
Pr ~ Pr_T(lumped_T)
f ~ Churchill_f(Re, e, dn) #Darcy-weisbach
alpha ~ Nusselt(Re, Pr, f)*lambda_T(lumped_T)/dn
Dxx ~ diffusion*Dxx_coeff(u, dn, lumped_T)
inlet.m ~ -outlet.m
inlet.p ~ outlet.p
inlet.T ~ instream(inlet.T)
outlet.T ~ T[N]
u ~ inlet.m/rho_T(inlet.T)/A
[C[i] ~ dx*A*rhocp_T(T[i]) for i in 1:N]
[S[i] ~ heatport.Q[i] for i in 1:N]
[Twall[i] ~ heatport.T[i] for i in 1:N]
#source term
[S[i] ~ (1/(1/(alpha*dn*pi*dx)+abs(Rw/1000)))*(Twall[i] - T[i]) for i in 1:N]
#second order upwind + diffusion + source
D(T[1]) ~ u/dx*(inlet.T - T[1]) + Dxx*(T[2]-T[1])/dx^2 + S[1]/(C[1]-C_shift)
D(T[2]) ~ u/dx*(c[1]*inlet.T - sum(c)*T[1] + c[2]*T[2] + c[3]*T[3]) + Dxx*(T[1]-2*T[2]+T[3])/dx^2 + S[2]/(C[2]-C_shift)
[D(T[i]) ~ u/dx*(c[1]*T[i-2] - sum(c)*T[i-1] + c[2]*T[i] + c[3]*T[i+1]) + Dxx*(T[i-1]-2*T[i]+T[i+1])/dx^2 + S[i]/(C[i]-C_shift) for i in 3:N-1]
D(T[N]) ~ u/dx*(T[N-1] - T[N]) + Dxx*(T[N-1]-T[N])/dx^2 + S[N]/(C[N]-C_shift)
]
ODESystem(eqs, t, sts, p; systems=[inlet, outlet, heatport], name=name)
end
function Cn_circular_wall_inner(d, D, cp, ρ)
C = pi/4*(D^2-d^2)*cp*ρ
return C/2
end
function Cn_circular_wall_outer(d, D, cp, ρ)
C = pi/4*(D^2-d^2)*cp*ρ
return C/2
end
function Ke_circular_wall(d, D, λ)
2*pi*λ/log(D/d)
end
function CircularWallFEM(;name, L=100, N=10, d=0.05, t_layer=[0.002],
λ=[50], cp=[500], ρ=[7850], T0=0.0)
@named inner_heatport = VectorHeatPort(N=N)
@named outer_heatport = VectorHeatPort(N=N)
dx = L/N
Ne = length(t_layer)
Nn = Ne + 1
dn = vcat(d, d .+ 2.0.*cumsum(t_layer))
Cn = zeros(Nn)
Cn[1:Ne] += Cn_circular_wall_inner.(dn[1:Ne], dn[2:Nn], cp, ρ).*dx
Cn[2:Nn] += Cn_circular_wall_outer.(dn[1:Ne], dn[2:Nn], cp, ρ).*dx
p = @parameters C_shift=0.0
Ke = Ke_circular_wall.(dn[1:Ne], dn[2:Nn], λ).*dx
@variables begin
(Tn(t))[1:N, 1:Nn] = fill(T0, N, Nn)
(Qe(t))[1:N, 1:Ne] = fill(T0, N, Ne)
end
sts = [vec(Tn); vec(Qe)]
eqs = [
[inner_heatport.T[i] ~ Tn[i,1] for i in 1:N]
[outer_heatport.T[i] ~ Tn[i,Nn] for i in 1:N]
[Qe[i,j] ~ Ke[j]*(-Tn[i,j+1]+Tn[i,j]) for i in 1:N for j in 1:Ne]...
[D(Tn[i,1])*(Cn[1]+C_shift) ~ inner_heatport.Q[i]-Qe[i,1] for i in 1:N]
[D(Tn[i,j])*Cn[j] ~ Qe[i,j-1]-Qe[i,j] for i in 1:N for j in 2:Nn-1]...
[D(Tn[i,Nn])*Cn[Nn] ~ Qe[i,Ne]+outer_heatport.Q[i] for i in 1:N]
]
ODESystem(eqs, t, sts, p; systems=[inner_heatport, outer_heatport], name=name)
end
function CylindricalSurfaceConvection(;name, L=100, N=100, d=1.0, α=5.0)
dx = L/N
S = pi*d*dx
@named heatport = VectorHeatPort(N=N)
sts = @variables Tenv(t)=0.0
eqs = [
Tenv ~ 18.0
[heatport.Q[i] ~ α*S*(heatport.T[i]-Tenv) for i in 1:N]
]
ODESystem(eqs, t, sts, []; systems=[heatport], name=name)
end
function PreinsulatedPipe(;name, L=100.0, N=100.0, dn=0.05, T0=0.0, t_layer=[0.004, 0.013],
λ=[50, 0.04], cp=[500, 1200], ρ=[7800, 40], α=5.0,
e=1e-4, lumped_T=50, diffusion=true)
@named inlet = FluidPort()
@named outlet = FluidPort()
@named fluid_region = FluidRegion(L=L, N=N, dn=dn, e=e, lumped_T=lumped_T, diffusion=diffusion)
@named shell = CircularWallFEM(L=L, N=N, d=dn, t_layer=t_layer, λ=λ, cp=cp, ρ=ρ)
@named surfconv = CylindricalSurfaceConvection(L=L, N=N, d=dn+2.0*sum(t_layer), α=α)
systems = [fluid_region, shell, inlet, outlet, surfconv]
eqs = [
connect(fluid_region.inlet, inlet)
connect(fluid_region.outlet, outlet)
connect(fluid_region.heatport, shell.inner_heatport)
connect(shell.outer_heatport, surfconv.heatport)
]
ODESystem(eqs, t, [], []; systems=systems, name=name)
end
function Source(;name, p_feed=100000)
@named outlet = FluidPort()
sts = @variables m_flow(t)=1e-6
eqs = [
m_flow ~ m_flow_source(t)
outlet.m ~ -m_flow
outlet.p ~ p_feed
outlet.T ~ T_source(t)
]
compose(ODESystem(eqs, t, sts, []; name=name), [outlet])
end
function Sink(;name)
@named inlet = FluidPort()
eqs = [
inlet.T ~ instream(inlet.T)
]
compose(ODESystem(eqs, t, [], []; name=name), [inlet])
end
function TestBenchPreinsulated(;name, L=1.0, dn=0.05, t_layer=[0.0056, 0.013], N=100, diffusion=true, lumped_T=20)
@named pipe = PreinsulatedPipe(L=L, dn=dn, N=N, diffusion=diffusion, t_layer=t_layer, lumped_T=lumped_T)
@named source = Source()
@named sink = Sink()
subs = [source, pipe, sink]
eqs = [
connect(source.outlet, pipe.inlet)
connect(pipe.outlet, sink.inlet)
]
compose(ODESystem(eqs, t, [], []; name=name), subs)
end
function test_speed(N; solver=Tsit5())
tspan = (0.0, 19*3600)
@named testbench = TestBenchPreinsulated(L=470, N=N, dn=0.3127, t_layer=[0.0056, 0.058])
sys = structural_simplify(testbench)
prob = ODEProblem(sys, [], tspan, jac=true, sparse=true)
prob.u0[:] .= 12.0
#TODO: unrecognized keywords jac and sparse in solve??
solve(prob, solver, reltol=1e-6, abstol=1e-6, saveat=100);
return @elapsed solve(prob, solver, reltol=1e-6, abstol=1e-6, saveat=100);
end
test_speed(1280)
# scaling tests
N_x = [5, 10, 20, 40, 80, 160, 320, 640, 1280]
N_states = 4 .* N_x
OMC_IDA_470 = [0.0125157, 0.0106602, 0.0172244, 0.0255715,
0.0567469, 0.126823, 0.247737, 0.622899, 1.32534]
JULIA_ODAE_Tsit5 = zeros(length(N_x))
for i in 1:length(N_x)
JULIA_ODAE_Tsit5[i] = test_speed(N_x[i], solver=Tsit5())
end
println(JULIA_ODAE_Tsit5)
#[0.071787957, 0.077838405, 0.095070696, 0.136035788, 0.227302308, 0.422744682, 0.90749644, 1.906403591, NaN]
JULIA_ODAE_QNDF = zeros(length(N_x))
for i in 1:length(N_x)
JULIA_ODAE_QNDF[i] = test_speed(N_x[i], solver=QBDF(linsolve=KLUFactorization()))
end
println(JULIA_ODAE_QNDF)
fig = plot(N_x, OMC_IDA, label="OMC IDA",
legend=:topleft, yscale=:log10, xscale=:log10,
xlim=(1,10000), ylim=(1e-3, 1e2), marker=:circle)
plot!(N_x, JULIA_ODAE_Tsit5, label="Julia ODAE Tsit5", marker=:square)
plot!(N_x, JULIA_ODAE_QNDF, label="Julia ODAE QNDF", marker=:star)
savefig(fig,"Scaling experiment.png")
|
|
Thanks for taking the time to run it again. For large and complex systems, symbolically computing the Jacobian won't be a good idea because the size of the expression will blowup, so I suggest you to use prob = ODEProblem(sys, [], tspan, sparse=true) |
|
Also, we are now defaulting to KLU for sparse matrices with moderate size, so you can just use |
|
BTW, the warning is fixed in #1895 |
|
I have modified the script a bit to make it friendlier to the compiler. Could you try this as well? using ModelingToolkit, OrdinaryDiffEq, Symbolics, IfElse, XSteam,
Polynomials, Plots, LinearSolve
# o o o o o o o < heat capacitors
# | | | | | | | < heat conductors
# o o o o o o o
# | | | | | | |
#Source -> o--o--o--o--o--o--o -> Sink
# advection diff source PDE
@variables t
D = Differential(t)
m_flow_source(t) = 2.75
T_source(t) = (t>12*3600)*56.0 + 12.0
@register_symbolic m_flow_source(t)
@register_symbolic T_source(t)
#build polynomial liquid-water property only dependent on Temperature
p_l = 5 #bar
T_vec = collect(1:1:150);
@noinline @generated kin_visc_T(t) = :(Base.evalpoly(t, $(fit(T_vec, my_pT.(p_l, T_vec)./rho_pT.(p_l, T_vec), 5).coeffs...,)))
@noinline @generated lambda_T(t) = :(Base.evalpoly(t, $(fit(T_vec, tc_pT.(p_l, T_vec), 3).coeffs...,)))
@noinline @generated Pr_T(t) = :(Base.evalpoly(t, $(fit(T_vec, 1e3*Cp_pT.(p_l, T_vec).*my_pT.(p_l, T_vec)./tc_pT.(p_l, T_vec), 5).coeffs...,)))
@noinline @generated rho_T(t) = :(Base.evalpoly(t, $(fit(T_vec, rho_pT.(p_l, T_vec), 4).coeffs...,)))
@noinline @generated rhocp_T(t) = :(Base.evalpoly(t, $(fit(T_vec, 1000*rho_pT.(p_l, T_vec).*Cp_pT.(p_l, T_vec), 5).coeffs...,)))
@register_symbolic kin_visc_T(t)
@register_symbolic lambda_T(t)
@register_symbolic Pr_T(t)
@register_symbolic rho_T(t)
@register_symbolic rhocp_T(t)
@connector function FluidPort(;name, p=101325.0, m=0.0, T=0.0)
sts = @variables p(t)=p m(t)=m [connect=Flow] T(t)=T [connect=Stream]
ODESystem(Equation[], t, sts, []; name=name)
end
@connector function VectorHeatPort(;name, N=100, T0=0.0, Q0=0.0)
sts = @variables (T(t))[1:N]=T0 (Q(t))[1:N]=Q0 [connect=Flow]
ODESystem(Equation[], t, [T; Q], []; name=name)
end
@register_symbolic Dxx_coeff(u, d, T)
#Taylor-aris dispersion model
@noinline function Dxx_coeff(u, d, T)
Re = abs(u)*d/kin_visc_T(T) + 0.1
IfElse.ifelse(Re < 1000, (d^2/4)*u^2/48/0.14e-6, d*u*(1.17e9*Re^(-2.5) + 0.41))
end
@register_symbolic Nusselt(Re, Pr, f)
#Nusselt number model
@noinline function Nusselt(Re, Pr, f)
if Re <= 2300
3.66
elseif Re <= 3100
3.5239*(Re/1000)^4-45.158*(Re/1000)^3+212.13*(Re/1000)^2-427.45*(Re/1000)+316.08
else
f/8*((Re-1000)*Pr)/(1+12.7*(f/8)^(1/2)*(Pr^(2/3)-1))
end
end
@register_symbolic Churchill_f(Re, epsilon, d)
#Darcy weisbach friction factor
@noinline function Churchill_f(Re, epsilon, d)
theta_1 = (-2.457*log(((7/Re)^0.9)+(0.27*(epsilon/d))))^16
theta_2 = (37530/Re)^16
8*((((8/Re)^12)+(1/((theta_1+theta_2)^1.5)))^(1/12))
end
function FluidRegion(;name, L=1.0, dn=0.05, N=100, T0=0.0,
lumped_T=50, diffusion=true, e=1e-4)
@named inlet = FluidPort()
@named outlet = FluidPort()
@named heatport = VectorHeatPort(N=N)
dx=L/N
c=[-1/8, -3/8, -3/8] # advection stencil coeficients
A = pi*dn^2/4
p = @parameters C_shift = 0.0 Rw = 0.0 # stuff for latter
@variables begin
(T(t))[1:N] = fill(T0, N)
Twall(t)[1:N] = fill(T0, N)
(S(t))[1:N] = fill(T0, N)
(C(t))[1:N] = fill(1.0, N)
u(t) = 1e-6
Re(t) = 1000.0
Dxx(t) = 0.0
Pr(t) = 1.0
alpha(t) = 1.0
f(t) = 1.0
end
sts = [T..., Twall..., S..., C..., u, Re, Dxx, Pr, alpha, f]
eqs = [
Re ~ 0.1 + dn*abs(u)/kin_visc_T(lumped_T)
Pr ~ Pr_T(lumped_T)
f ~ Churchill_f(Re, e, dn) #Darcy-weisbach
alpha ~ Nusselt(Re, Pr, f)*lambda_T(lumped_T)/dn
Dxx ~ diffusion*Dxx_coeff(u, dn, lumped_T)
inlet.m ~ -outlet.m
inlet.p ~ outlet.p
inlet.T ~ instream(inlet.T)
outlet.T ~ T[N]
u ~ inlet.m/rho_T(inlet.T)/A
[C[i] ~ dx*A*rhocp_T(T[i]) for i in 1:N]
[S[i] ~ heatport.Q[i] for i in 1:N]
[Twall[i] ~ heatport.T[i] for i in 1:N]
#source term
[S[i] ~ (1/(1/(alpha*dn*pi*dx)+abs(Rw/1000)))*(Twall[i] - T[i]) for i in 1:N]
#second order upwind + diffusion + source
D(T[1]) ~ u/dx*(inlet.T - T[1]) + Dxx*(T[2]-T[1])/dx^2 + S[1]/(C[1]-C_shift)
D(T[2]) ~ u/dx*(c[1]*inlet.T - sum(c)*T[1] + c[2]*T[2] + c[3]*T[3]) + Dxx*(T[1]-2*T[2]+T[3])/dx^2 + S[2]/(C[2]-C_shift)
[D(T[i]) ~ u/dx*(c[1]*T[i-2] - sum(c)*T[i-1] + c[2]*T[i] + c[3]*T[i+1]) + Dxx*(T[i-1]-2*T[i]+T[i+1])/dx^2 + S[i]/(C[i]-C_shift) for i in 3:N-1]
D(T[N]) ~ u/dx*(T[N-1] - T[N]) + Dxx*(T[N-1]-T[N])/dx^2 + S[N]/(C[N]-C_shift)
]
ODESystem(eqs, t, sts, p; systems=[inlet, outlet, heatport], name=name)
end
@register_symbolic Cn_circular_wall_inner(d, D, cp, ρ)
function Cn_circular_wall_inner(d, D, cp, ρ)
C = pi/4*(D^2-d^2)*cp*ρ
return C/2
end
@register_symbolic Cn_circular_wall_outer(d, D, cp, ρ)
function Cn_circular_wall_outer(d, D, cp, ρ)
C = pi/4*(D^2-d^2)*cp*ρ
return C/2
end
@register_symbolic Ke_circular_wall(d, D, λ)
function Ke_circular_wall(d, D, λ)
2*pi*λ/log(D/d)
end
function CircularWallFEM(;name, L=100, N=10, d=0.05, t_layer=[0.002],
λ=[50], cp=[500], ρ=[7850], T0=0.0)
@named inner_heatport = VectorHeatPort(N=N)
@named outer_heatport = VectorHeatPort(N=N)
dx = L/N
Ne = length(t_layer)
Nn = Ne + 1
dn = vcat(d, d .+ 2.0.*cumsum(t_layer))
Cn = zeros(Nn)
Cn[1:Ne] += Cn_circular_wall_inner.(dn[1:Ne], dn[2:Nn], cp, ρ).*dx
Cn[2:Nn] += Cn_circular_wall_outer.(dn[1:Ne], dn[2:Nn], cp, ρ).*dx
p = @parameters C_shift=0.0
Ke = Ke_circular_wall.(dn[1:Ne], dn[2:Nn], λ).*dx
@variables begin
(Tn(t))[1:N, 1:Nn] = fill(T0, N, Nn)
(Qe(t))[1:N, 1:Ne] = fill(T0, N, Ne)
end
sts = [vec(Tn); vec(Qe)]
eqs = [
[inner_heatport.T[i] ~ Tn[i,1] for i in 1:N]
[outer_heatport.T[i] ~ Tn[i,Nn] for i in 1:N]
[Qe[i,j] ~ Ke[j]*(-Tn[i,j+1]+Tn[i,j]) for i in 1:N for j in 1:Ne]...
[D(Tn[i,1])*(Cn[1]+C_shift) ~ inner_heatport.Q[i]-Qe[i,1] for i in 1:N]
[D(Tn[i,j])*Cn[j] ~ Qe[i,j-1]-Qe[i,j] for i in 1:N for j in 2:Nn-1]...
[D(Tn[i,Nn])*Cn[Nn] ~ Qe[i,Ne]+outer_heatport.Q[i] for i in 1:N]
]
ODESystem(eqs, t, sts, p; systems=[inner_heatport, outer_heatport], name=name)
end
function CylindricalSurfaceConvection(;name, L=100, N=100, d=1.0, α=5.0)
dx = L/N
S = pi*d*dx
@named heatport = VectorHeatPort(N=N)
sts = @variables Tenv(t)=0.0
eqs = [
Tenv ~ 18.0
[heatport.Q[i] ~ α*S*(heatport.T[i]-Tenv) for i in 1:N]
]
ODESystem(eqs, t, sts, []; systems=[heatport], name=name)
end
function PreinsulatedPipe(;name, L=100.0, N=100.0, dn=0.05, T0=0.0, t_layer=[0.004, 0.013],
λ=[50, 0.04], cp=[500, 1200], ρ=[7800, 40], α=5.0,
e=1e-4, lumped_T=50, diffusion=true)
@named inlet = FluidPort()
@named outlet = FluidPort()
@named fluid_region = FluidRegion(L=L, N=N, dn=dn, e=e, lumped_T=lumped_T, diffusion=diffusion)
@named shell = CircularWallFEM(L=L, N=N, d=dn, t_layer=t_layer, λ=λ, cp=cp, ρ=ρ)
@named surfconv = CylindricalSurfaceConvection(L=L, N=N, d=dn+2.0*sum(t_layer), α=α)
systems = [fluid_region, shell, inlet, outlet, surfconv]
eqs = [
connect(fluid_region.inlet, inlet)
connect(fluid_region.outlet, outlet)
connect(fluid_region.heatport, shell.inner_heatport)
connect(shell.outer_heatport, surfconv.heatport)
]
ODESystem(eqs, t, [], []; systems=systems, name=name)
end
function Source(;name, p_feed=100000)
@named outlet = FluidPort()
sts = @variables m_flow(t)=1e-6
eqs = [
m_flow ~ m_flow_source(t)
outlet.m ~ -m_flow
outlet.p ~ p_feed
outlet.T ~ T_source(t)
]
compose(ODESystem(eqs, t, sts, []; name=name), [outlet])
end
function Sink(;name)
@named inlet = FluidPort()
eqs = [
inlet.T ~ instream(inlet.T)
]
compose(ODESystem(eqs, t, [], []; name=name), [inlet])
end
function TestBenchPreinsulated(;name, L=1.0, dn=0.05, t_layer=[0.0056, 0.013], N=100, diffusion=true, lumped_T=20)
@named pipe = PreinsulatedPipe(L=L, dn=dn, N=N, diffusion=diffusion, t_layer=t_layer, lumped_T=lumped_T)
@named source = Source()
@named sink = Sink()
subs = [source, pipe, sink]
eqs = [
connect(source.outlet, pipe.inlet)
connect(pipe.outlet, sink.inlet)
]
compose(ODESystem(eqs, t, [], []; name=name), subs)
end |
|
I started Julia with O0, and with N=2000, I got julia> sol = @time solve(prob, solver, reltol=1e-6, abstol=1e-6, saveat=100);
3923.945535 seconds (363.26 M allocations: 99.133 GiB, 54.01% gc time, 99.85% compilation time)
julia> sol = @time solve(prob, solver, reltol=1e-6, abstol=1e-6, saveat=100);
5.670703 seconds (170.91 k allocations: 84.112 MiB)I have 16 GB of RAM on my laptop as well. |
|
The process still gets killed on my machine, but I have realized that my laptop has tiny SWAP file (only 2 GB) so it probably does not have any place to fit in memory and my OS just kills it to stay alive. I will try different machine with 16 GB of RAM and I will increase the SWAP area on my laptop to see if it changes anything. BTW: |
|
On my laptop on Julia 1.9 (nightly release from today) and |
|
I have tried N=10000 in Julia-1.9.0-beta3 with -O2 ]st I changed some stuff a little: function CircularWallFEM(;name, L=100, N=10, d=0.05, t_layer=[0.002],
λ=[50], cp=[500], ρ=[7850], T0=0.0)
@named inner_heatport = VectorHeatPort(N=N)
@named outer_heatport = VectorHeatPort(N=N)
dx = L/N
Ne = length(t_layer)
Nn = Ne + 1
dn = vcat(d, d .+ 2.0.*cumsum(t_layer))
Cn = zeros(Nn)
Cn[1:Ne] += Cn_circular_wall_inner.(dn[1:Ne], dn[2:Nn], cp, ρ).*dx
Cn[2:Nn] += Cn_circular_wall_outer.(dn[1:Ne], dn[2:Nn], cp, ρ).*dx
Ke = Ke_circular_wall.(dn[1:Ne], dn[2:Nn], λ).*dx
@variables begin
(Tn(t))[1:N, 1:Nn] = fill(T0, N, Nn)
(Qe(t))[1:N, 1:Ne] = fill(T0, N, Ne)
end
sts = [vec(Tn); vec(Qe)]
eqs = [
[inner_heatport.T[i] ~ Tn[i,1] for i in 1:N]
[outer_heatport.T[i] ~ Tn[i,Nn] for i in 1:N]
#using vec() instead of ... because it throws stack overflow
vec([Qe[i,j] ~ Ke[j]*(-Tn[i,j+1]+Tn[i,j]) for i in 1:N for j in 1:Ne])
# I moved the Cn[j] to RHS because it simplifies differently (mass matrices)
[D(Tn[i,1]) ~ (inner_heatport.Q[i]-Qe[i,1])/Cn[1] for i in 1:N]
vec([D(Tn[i,j]) ~ (Qe[i,j-1]-Qe[i,j])/Cn[j] for i in 1:N for j in 2:Nn-1])
[D(Tn[i,Nn]) ~ (Qe[i,Ne]+outer_heatport.Q[i])/Cn[Nn] for i in 1:N]
]
ODESystem(eqs, t, sts, []; systems=[inner_heatport, outer_heatport], name=name)
end
function pulse(t; height=5.0, width=3600, period=7200)
i = div(t, period)
if t-i*period < width
return height
else
return 0.0
end
end
@register_symbolic pulse(t)
function Source(;name, p_feed=100000)
@named outlet = FluidPort()
sts = @variables m_flow(t)=1e-6
eqs = [
m_flow ~ 10.0
outlet.m ~ -m_flow
outlet.p ~ p_feed
outlet.T ~ 12.0 + pulse(t) # makes stuff happen all the time (stress test)
]
compose(ODESystem(eqs, t, sts, []; name=name), [outlet])
end
function test_speed_preinsulated(N; solver=Tsit5(), jac=true)
println("Building N=$N")
tspan = (0.0, 24*3600)
@named testbench = TestBenchPreinsulated(L=10000, N=N, dn=0.3127, t_layer=[0.0056, 0.058])
println("Simplifying N=$N")
sys = structural_simplify(testbench)
println("Bulding ODE problem N=$N")
prob = ODEProblem(sys, [], tspan, jac=jac, sparse=true)
prob.u0[:] .= 12.0
#TODO: unrecognized keywords jac and sparse in solve??
println("First solve N=$N")
et_first = @elapsed sol = solve(prob, solver, reltol=1e-6, abstol=1e-6, saveat=100);
println("Second solve N=$N")
return sol, et_first, minimum([@elapsed solve(prob, solver, reltol=1e-6, abstol=1e-6, saveat=100) for i in 1:5]);
endSecond solve Julia: 74.938 s with QNDF(autodiff=false) The compilation took whole night (first run 54899.91 s) on Intel Xeon Gold 6230 with 188 GB of RAM. So I think we can say that MTK + OrdinaryDiffEq beats the OMC performance quite confidently. |
Since you are using connectors with stream variables, it'd be good to try it with #2049. |
|
That was not it. new ]st QNDF(autodiff=false) Tsit5() |
|
We need to clarify what is "compilation" time. I think @LiborKudela is talking about Julia compilation time for the RHS and the Jacobian of the DAE definition. @visr is talking about MTK connection expansion time. They have almost nothing to do with each other, so 2049 likely won't help. |
|
Yes, but I forgot to mention that jac was set to false. res = test_speed_preinsulated(10000, solver=QNDF(autodiff=false), jac=false)So is it just the RHS? |
|
It's just the righthand side. It builds a scalarized version without loops, which is then like a Julia functions with tens of thousands of lines, which then gets sent to LLVM for optimization and gets stuck optimizing forever. It needs to (a) retain structure and (b) handle LLVM inference better. There were some changes for newer versions of Julia such as JuliaLang/julia#43852 which are 1000x faster in some MTK-related cases, so trying v1.9 or the nightly could show some improvements. but that would only be looking at (b), so the "best" case would still need (a) (which is actively in progress). |
|
If we are not compiling Jacobian, why would QNDF take much longer to compile than Tsit5? |
|
Sorry that was my mistake. res = test_speed_preinsulated(10000, solver=QNDF(autodiff=false), jac=false)and it had to call the same compiled functions internally when I ran the Tsit5 afterwards in the same session res = test_speed_preinsulated(10000, solver=Tsit5(), jac=false)I was just going to ask how it could happen? As if it memoizes something even if it is wrapped inside the test_speed_preinsulated. I am running the Tsit5 compile in fresh session now - I expect similar compile time as with QNDF. |
|
The value 10000 is somewhere converted to a Type right? Otherwise it would not dispatch by value correct? |
|
RuntimeGeneratedFunctions.jl (RGF) caches the expression of a function in a dictionary, and we make sure to generate the same expression for the same model given the same version of packages. Thus, RGF would always invoke the same object for RHS evaluation. |
|
If the cache does not clear itself, it would explain why my original performance test ran out of 16GB RAM and when @YingboMa ran only the single N=2000 it did not. My test was creating these RGF objects in a loop and keeping them in memory so my OS had to kill the whole session. It is not very evident for a user of MTK though. It would be good thing to have in the docs if it is not already there, I have certainly missed it. |
|
The Tsit5 first run with N=10000 takes 50918.319 seconds as expected. |
|
@ChrisRackauckas do you have a rough idea for when "retain structure" will be available? Is it mostly work in ModelingToolkit itself, making use of the tags that were added in #1866? |
|
Hopefully this is the focus of the next 6 months 😅 |
prob.u0[:] .= 12.0Why are all of the initializations in the julia code changed to 12 but not in the Modelica code? That completely changes the problem? |
|
The problem is generally solved by JuliaSimCompiler. It has now been turned into a canonical benchmark to track performance, with automatically running OpenModelica as well, in SciML/SciMLBenchmarks.jl#949. There's also Dymola timings. We'll use that benchmark to continue development. But from the early results https://docs.sciml.ai/SciMLBenchmarksOutput/dev/ModelingToolkit/ThermalFluid/ JSC fixes this by a few orders of magnitude and thus we recommend the alternative compiler backend for any sufficiently large problem. |
|
The intention of The Modelica code has the equivalent in the The line in Models.PreinsulatedPipe preinsulatedPipe(L = 470, N = 1280, T0 = 12, dn = 0.3127)The line in sub-components are: DhnControl.Models.FluidRegion fluidRegion(L=L, N=N, dn=dn, T0=T0, lumped_T=lumped_T,eps=eps)
DhnControl.Models.CylindricalWallFem cylindricalWallFem(t_layer=t_layer, L=L, N=N, d=dn, rho=rho, lambda=lambda, cp=cp, T0=T0) and then they propagate it further down to the actual variables: Real Tn[N,Nn](each start = T0); //CylindricalWallFem
Real T[N](each start = T0); //FluidRegion
Real Twall[N](each start = T0); //FluidRegionI hope this clarifies it a little. |
|
Okay I'll add it back into the benchmark. |
|
Thank you all, for doing such an awesome job with the MTK and all the other stuff in Julia !! 💯 |




Hi,
I am playing with MTK and OpenModelica (OMC). I have written a model of pipe (1D advection-diffusion-source PDE) that uses second order upwind scheme. The pipe is surrounded with two layers of solid matter (heat equation) and is connected to the pipe via heatport (connector) that has vector variables in it. The pipe and the solid are discretized into N pieces. I have written the exact same model in Modelica.
The model agrees with experimental data so it should be correct.
I have compared the performance and I cannot beat the OMC performance with MTK + OrdinaryDiffEq for higher N (x-N, y-cputime).
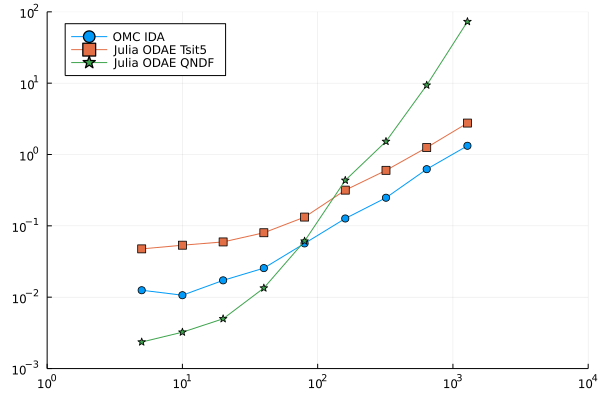
(the number of states is 4*N btw)
I have tried quite a bunch of options but Tsit5 and QNDF look most promising.
The Tsit5() scales the same as OMC but is approximately. twice slower - > I am happy.
The QNDF(autodiff=false) is quite faster for small N but scales quite bad.
Why does QNDF scale this bad with N?
Is there some other solvers I can try, or some other solver options etc.?
(I also tried IDA() from Sundials.jl, but it was no good either.)
Should I even expect to beat OMC with Julia like this?
Thank you for any response
The MTK model:
Modelica Version:
]st
[6e4b80f9] BenchmarkTools v1.3.1
[336ed68f] CSV v0.10.4
[052768ef] CUDA v3.11.0
[a93c6f00] DataFrames v1.3.4
[82cc6244] DataInterpolations v3.9.2
[39dd38d3] Dierckx v0.5.2
[aae7a2af] DiffEqFlux v1.51.2
[41bf760c] DiffEqSensitivity v6.79.0
[0c46a032] DifferentialEquations v7.2.0
[f6369f11] ForwardDiff v0.10.30
[615f187c] IfElse v0.1.1
[a98d9a8b] Interpolations v0.14.0
[ef3ab10e] KLU v0.3.0
[7f56f5a3] LSODA v0.7.0
[b964fa9f] LaTeXStrings v1.3.0
[7ed4a6bd] LinearSolve v1.20.0
[eff96d63] Measurements v2.7.2
[961ee093] ModelingToolkit v8.15.1
[7f7a1694] Optimization v3.7.1
[1dea7af3] OrdinaryDiffEq v6.18.1
[f0f68f2c] PlotlyJS v0.18.8
[91a5bcdd] Plots v1.31.2
[f27b6e38] Polynomials v3.1.4
[1fd47b50] QuadGK v2.4.2
[731186ca] RecursiveArrayTools v2.31.1
[276daf66] SpecialFunctions v2.1.7
[43dc94dd] SteamTables v1.3.0
[c3572dad] Sundials v4.9.4
[0c5d862f] Symbolics v4.9.0
[a759f4b9] TimerOutputs v0.5.20
[95ff35a0] XSteam v0.3.0
OMC
OpenModelica v1.19.2
The text was updated successfully, but these errors were encountered: