Skip to content

Latest commit

 

History

History
128 lines (91 loc) · 6.27 KB

README.md

File metadata and controls

128 lines (91 loc) · 6.27 KB
Raw

SELF BALANCING

TABLE OF CONTENTS

How bot balance itself?

Theory

  • Suppose that the bot is initially stationary. If it moves forward the front of the bot goes upwards and vice versa for when we move the bot backwards.
  • Likewise, if the bot is above its desired position we can move the bot backwards to bring the bot to desired position.
  • And if bot is below its desired position we can move the bot forward to bring the bot to desired position.
  • This way we can decide the direction the bot moves in i.e. forwards or backwards in order to maintain its balance.

Use of PID

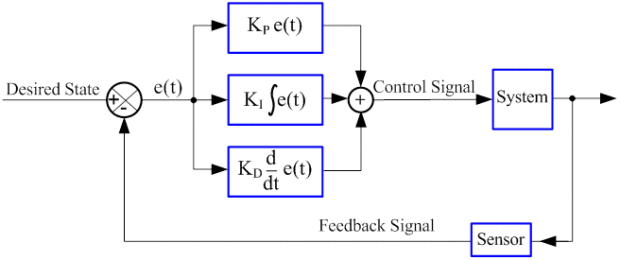
PID stands for Proportional-Integral-Derivative

  • The desired state is the position you want your robot to be in. In the case of the balancing robot, that would be straight up and down.
  • The e(t) part is the error experienced.
  • The Kp * e(t) part is the Proportional part.
  • The Ki * integral e(t) part is the Integral part.
  • The Kd * d/dt e(t) part is the Derivative part
  • The + means they are all added together into a control signal that is passed on to the system. In our case the system is a self balancing robot. The control signal tells the how fast ESP to move the motors in order to balance the robot.
  • Finally the sensor (the MPU-6050 in our case) sends the new current position of the robot back to the ESP, which calculates the error and does the whole process again. This is called feedback, and makes this type of control loop a closed-loop system (as opposed to an open-loop system, which is easier but much less accurate).

Proportional Term

The proportional term (gain) makes a change to the output that is proportional to the current error value.

  • Now correction_speed = Kp * Error (Here Kp is the proportionality constant)
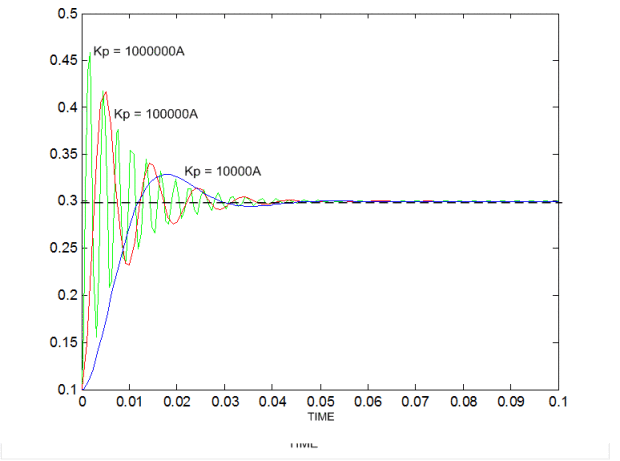
  • If Kp is Too Low , Say Kp = 0.05 , now for Error = 5 the correction_speed=0.25 which is insignificant for our motors
  • If Kp is too high , Say Kp = 10 , now for Error = 5, then correction_speed = 50 , which is marginally high for such small error. Hence, the bot will overshoot and pass through the 0 degree mark and towards the negative side .

Derivative Term

The derivative term slows the rate of change of the controller output, most notably near the controller set value.The Kd term helps the Kp term not overshoot the mark and reduces oscillations. Too large of a Kd term will slow down the response of the robot and make it slower to balance, while too small of a Kd term will make it shake a lot.

  • If you try to Balance the Bot using just the Proportional Term ,by providing proper 'Kp' value The bot will balance but will oscillate near the Origin. We need to dampen these oscillations , we introduce a new term known as the Derivative Term.
  • Correction_Speed = Kp * Error + Kd *Error_Rate
  • Error_Rate= (Current_Error - Previous_Error)/dt
  • Suppose we have Kp such that error changes from 100 to 50 in one second , Now for this particular Instant, the Error_Rate = -50 ,Correction_Rate = Kp50 + Kd(-50) ----- (A)

Integral Term

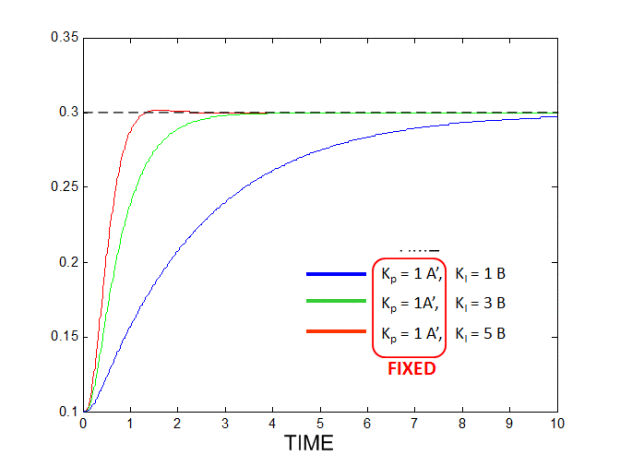
The Integral term is proportional to the amount of time the error is present. The integral term accelerates the movement of the process towards the set value and eliminates any residual steady-state error that occurs with a proportional only controller.

  • For example, if the MPU should read 181 degrees to be balanced, but reads 181.1, that might not be enough to move the motors enough to correct for that 0.1 difference. But if the MPU reads that value 100 times in a second, the extra 0.1 degree becomes 10 degrees of cumulative error, and that IS enough to move the motors.
  • Once the bot reaches the target, it will drift towards the other side because the cumulative error has already been built up once it passes to the other side, the error will add up with opposite sign and slowly decrease the cumulative error stabilizing the bot back to the target point.
  • This can have negative consequences if the Ki error is too large though, as shown here:

Formula for calculation of pitch correction

pitch_correction = Kp*(error) + Ki*(Integral_Error) + Kd*(Error_rate)

Proportional Term = kp*(Error)

Derivative Term = kd*(Error_rate)

Integral Term = ki*(Integral_Error)

ALGORITHM

  1. Reading data from sensors and Calculate Error.
  2. Calculate “Error Rate” and “Cumulative Error(Integral)” Terms.
  3. Calculate Correction Speed Using PID Equation.
  4. Threshold Correction Speed to MAX and MIN PWM.
  5. Direction in which bot should move:
    1. If Error > 1 (Bot-front is down) : bot_forward(pwm)
    2. If Error <-1 (Bot-front is up) : bot_backward(pwm)
    3. else (bot is balanced) : bot_stop()
  6. Go to Step 1.

Description of the functions

  •   void calculate_motor_command(const float pitch_error, float *motor_cmd)

    Description : Calucate the motor inputs according to the angle of MPU

    Parameters :

    • pitch_error : value of the error between desired angle and current angle
    • motor_cmd : Pointer to variable motor_cmd which will store the calculated correction values
  •   void balance_task(void *arg)

    Description : The main task to balance the bot

  •   read_mpu6050(euler_angle, mpu_offset)

    Description : to read the mpu6050 and calucation of the complimentary pitch and roll angles

    Parameters :

    • euler angle: euler_angles are the complementary pitch and roll angles obtained from mpu6050
    • mpu_offset : mpu_offsets are the initial accelerometer angles at rest position

    Return : returns ESP_OK if calculate angles correctly else return ESP_FAIL if any error occurs