Red Black Trees are self-balancing binary search trees (BST) which add one bit of memory to the standard implementation (usually denoted by the colours red and black). With this additional tracking information; the worst case search, insert and delete time complexity drops to O(log N) [from O(N) in the BST case].
Sounds great and all, but what the hell does that mean?
Generally speaking, a BST stores your information in a structured (sorted) manner, such that on average an operation can ignore about half of the tree before identifying the correct node to work with. The time taken for this operation is proportional to the logarithm of the number (N) of items in the tree, i.e. log N — a good deal better than the linear time lookup O(N) for an unsorted list. A hashmap on the other hand does even better: on average it only takes O(1) time, meaning it usually can just go to the correct node directly.
Notice though, that these are the average cases.
What about the worst case?
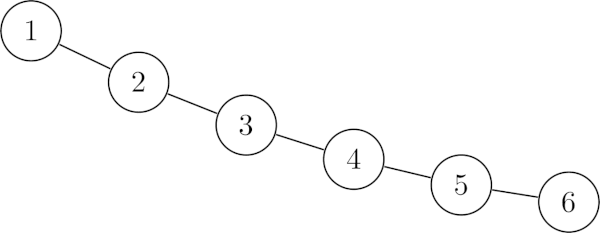
Consider you have a sorted list [ 1, 2, 3, 4, 5, 6 ] that you convert to a BST.
As each number is inserted, the algorithm will find that it must go to the right child branch of the tree, since it is larger than the previous one.
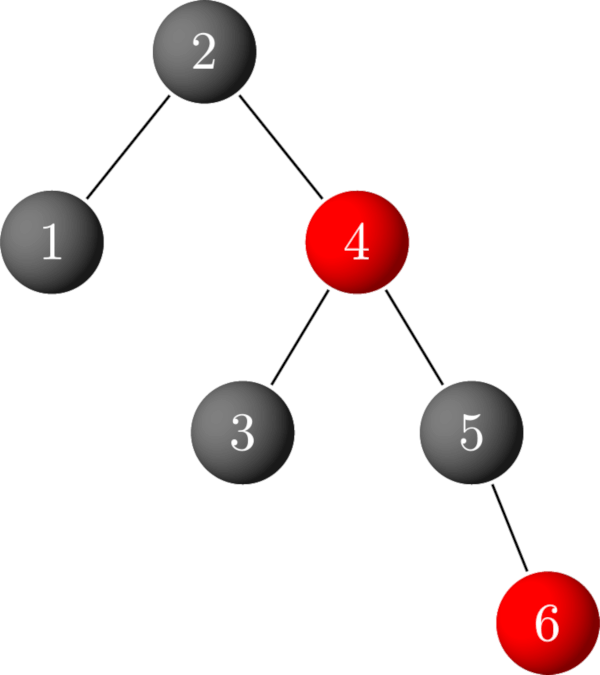
In the end, you get a lopsided tree:
Now, if you wish to insert a 7, you must traverse all of the values in the tree before arriving at the place you need to go.
Thus, your operation is going to take O(N) here, not the average O(log N).
A hashmap has the same sticking point, so for the most part, they are fast but can get into big trouble sometimes.
I thought this library was for red black trees. What's with all this binary search and hashmap malarkey?
Right. So red black trees fix the worst case scenario problem with some fancy trickery.
The colours allow the tree to arrange itself such that the height of the tree is minimised, or in other words, the tree remains balanced.
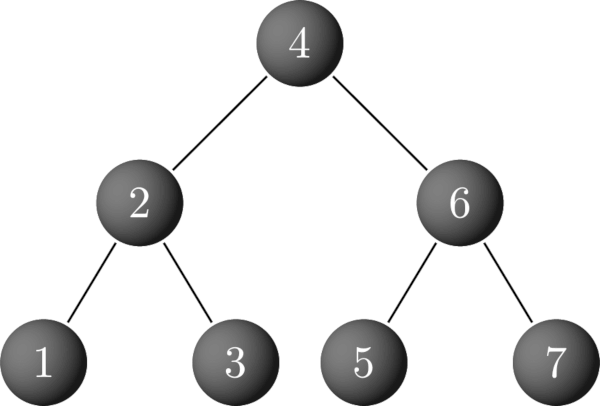
It becomes even better once we successfully insert the 7:
All operations work in O(log N) time, meaning consistent performance across all cases. Therefore you should be using a red black tree over a standard binary search tree whenever possible, and whenever your hashmap is giving you grief.
Hold up, why does this package exist? Isn't this just the poor-man's version of Elm's
Dictimplementation?
Well… Yes. Would you believe that I only realised this after I'd written the entire codebase and was just finishing off this documentation? Usually dictionaries are hashmaps under the hood. Seems that Elm's design principles are in line with the 'consistent performance' ideals mentioned above.
So let me be clear: you probably want to be using Dict in your app.
The implementation herein is closer to the Elm 0.18 Dict than the 0.19 one, but both of these are a bit difficult to read and understand. This codebase is well documented and as simple as a red black tree can be. Therefore, its purpose is perhaps more educational than anything else.