-
Notifications
You must be signed in to change notification settings - Fork 13
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
DynPoint? Estimating Velocity #60
Comments
|
Hi, thanks! The idea is to add velocity states to Maybe we could use the variable name I've made a few changes, here is what I think. If we're good, I will bring the code in with a pull request and reference the issue there. struct DynPoint2 <: IncrementalInference.InferenceVariable
ut::Int64 # microsecond time
dims::Int
labels::Vector{String}
DynPoint2() = new(0, 4, String[]) # x, dy/dt, x, dy/dt,
DynPoint2(ut::Int64) = new(ut, 4, String[]) # x, dy/dt, x, dy/dt,
endI don't think you want to keep time stamps as free variables to be estimated (although that is entirely okay to do if you wanted)? For this I think the dimension of the node is still only 4, but there is metadata to store in the variable node also. I also dropped the "Point4" variable node name from the labels, to reduce the amout of data in stored in the database, but can certainly add it if you wanted to query against these variable types. mutable struct DynPoint2DynPoint2 <: IncrementalInference.FunctorPairwise where {T <: Distribution}
z::T
DynPoint2DynPoint2{T}() where {T <: Distribution} = new{T}()
DynPoint2DynPoint2(z1::T) where {T <: Distribution} = new{T}(z1)
DynPoint2DynPoint2(mean::Vector{Float64}, cov::Array{Float64,2}) where {T <: Distribution} = new{Distributions.MvNormal}(MvNormal(mean, cov))
end
getSample(dp2dp2::DynPoint2DynPoint2, N::Int=1) = (rand(s.z,N), )
function (dp2dp2::DynPoint2DynPoint2)(res::Array{Float64},
idx::Int,
meas::Tuple,
Xi::Array{Float64,2},
Xj::Array{Float64,2} )
Z = meas[1][1,idx]
xi, xj = Xj[:,idx],Xj[:,idx]
# dt = xj[5] - xi[5] # I see the problem, you no longer have access to time stamps that were stored in the variable nodes -- TODO
res[1:2] = z[1:2] - (xj[1:2] - (xi[1:2]+dt*xi[3:4]))
res[3:4] = z[3:4] - (xj[3:4] - xi[3:4])
nothing
endThe I also added the indexing for This example will require some solver code changes (thanks for pointing them out) -- we will need the ability to pass DynPoint2DynPoint2 variable node meta data down to the residual function. I will get right on that and open a new issue / feature request to track that. Lastly, should we make the residual function calculate the |
|
See progress here: Pending change to solver first: Merging sequence to prepare RoME.jl first, then merge to METADATA.jl with new release, then changes in IncrementalInference.jl can be tagged and merged to METADATA.jl also. |
|
Hi @mc2922 , please see the new test code here: If you want to test with both IncrementalInference and RoME on branches, they would be:
else, hold off till these are merged into master branch -- will do that in a few days. There is one non-obvious thing to be aware of: If you look at the test example you will see the second pose I'm personally comfortable with using "delta position plus" given background in inertial odometry preintegrals. We would have to communicate all this clearly. Thanks for filing the issue / request and code! |
|
Let me read up on the pre-integrals, I'm not too familiar. Will edit this comment after.
|
|
Thanks for the write up! From this:
I see that the pose vector is [x y xdot ydot]? but here:
You are referencing [1:2] as position, and [3:4] as the velocity? This initialization should set point 1 to (10,10) with velocities (0.1,0.1)? I would still expect the positions of pt2 to come out very close to 10,10?
|
|
I read [1] for the preintegration explanation.
I wonder if we should tackle the more general problem right away, i.e. assume that odometry will be in a local frame only, and encode bearing + rotation in and out of local/global frames? Or do you think we should get a working example with the current code first? If that case, I'm hesitant about the midpoint integration. It would make sense if we obtain many odometric measurements quickly, (dt small), but if (dt large), its like a baked in time lag filter, might as well use just the new position. Makes sense to have two factor-types probably, one with each? |
correct.
I understand you to mean
Incorrect, fg = initfg()
v0 = addNode!(fg, :x0, DynPoint2(ut=0))
# Prior factor as boundary condition
pp0 = DynPoint2VelocityPrior(MvNormal([zeros(2);10*ones(2)], 0.1*eye(4)))
f0 = addFactor!(fg, [:x0;], pp0)The prior puts position at [0,0] and velocity at [10,10], both with normally distributed confidence of 0.1. By looking at the values in using KernelDensityEstimate
@show x0 = getKDEMax(getVertKDE(fg, :x0))
# julia> ... = [-0.19441, 0.0187019, 10.0082, 10.0901]
This is the "delta position plus" thing of eq. (1) I'm trying to indicate. At this point there at two options for factors that drive velocity, I think the names would be
That would be good yes.
If I am understanding you correctly, that is precisely what the current code is already doing. The likelihood (or The values stored in @show x0 = getKDEMax(getVertKDE(fg, :x0))
# julia> ... = [-0.19441, 0.0187019, 10.0082, 10.0901]
@show x1 = getKDEMax(getVertKDE(fg, :x1))
# julia> ... = [19.9072, 19.9765, 10.0418, 10.0797]
I want to add the
No problem, lets leave it out for now, and easy to add once the desired work flow is clear.
I will get on that --
PS, (author disclosure) you can find a continuous-time, higher order preintegration derivation (a formal Taylor expansion) and discussion in Chapter 4 too, as well as independently developed. |
|
HI @mc2922 , so here is a better example where I use a slightly different pipeline for enforcing the residual functions, i.e. mutable struct VelPoint2VelPoint2{T} <: IncrementalInference.FunctorPairwiseMinimize where {T <: Distribution}
z::T
VelPoint2VelPoint2{T}() where {T <: Distribution} = new{T}()
VelPoint2VelPoint2(z1::T) where {T <: Distribution} = new{T}(z1)
end
getSample(vp2vp2::VelPoint2VelPoint2, N::Int=1) = (rand(vp2vp2.z,N), )
function (vp2vp2::VelPoint2VelPoint2)(
res::Array{Float64},
userdata,
idx::Int,
meas::Tuple,
Xi::Array{Float64,2},
Xj::Array{Float64,2} )
#
z = meas[1][:,idx]
xi, xj = Xi[:,idx], Xj[:,idx]
dt = (userdata.variableuserdata[2].ut - userdata.variableuserdata[1].ut)*1e-6 # roughly the intended use of userdata
dp = (xj[1:2]-xi[1:2])
dv = (xj[3:4]-xi[3:4])
res[1] = 0.0
res[1] += sum((z[1:2] - dp).^2)
res[1] += sum((z[3:4] - dv).^2)
res[1] += sum((dp/dt - xi[3:4]).^2) # (dp/dt - 0.5*(xj[3:4]+xi[3:4])) # midpoint integration
res[1]
endNow the example works a little closer to what you may have expected: fg = initfg()
# add three point locations
v0 = addNode!(fg, :x0, DynPoint2(ut=0))
v1 = addNode!(fg, :x1, DynPoint2(ut=1000_000))
v2 = addNode!(fg, :x2, DynPoint2(ut=2000_000))
# Prior factor as boundary condition
pp0 = DynPoint2VelocityPrior(MvNormal([zeros(2);10*ones(2)], 0.1*eye(4)))
f0 = addFactor!(fg, [:x0;], pp0)
# conditional likelihood between Dynamic Point2
dp2dp2 = VelPoint2VelPoint2(MvNormal([10*ones(2);zeros(2)], 0.1*eye(4)))
f1 = addFactor!(fg, [:x0;:x1], dp2dp2)
# conditional likelihood between Dynamic Point2
dp2dp2 = VelPoint2VelPoint2(MvNormal([10*ones(2);zeros(2)], 0.1*eye(4)))
f2 = addFactor!(fg, [:x1;:x2], dp2dp2)
# Graphs.plot(fg.g)
ensureAllInitialized!(fg)
tree = wipeBuildNewTree!(fg)
inferOverTree!(fg, tree)
# see the output
@show x0 = getKDEMax(getVertKDE(fg, :x0))
@show x1 = getKDEMax(getVertKDE(fg, :x1))
@show x2 = getKDEMax(getVertKDE(fg, :x2))Producing output: |
|
I'm also working on the write-up for defining your own factors. This will become part of the general Caesar documentation. |
|
please see new documentation here: |
|
See new |
|
See new tag RoME v0.1.4 which also requires upcoming |
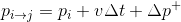


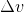
Dyn point is not the most satisfying name, since we may want a point also with accelerations?
DOF is misleading
Have to think about the name
What about ->
The text was updated successfully, but these errors were encountered: