Discussion: should we use divide-and-conquer reduce for instruction-level parallelism?

[tkf]

As I discussed briefly with @c42f in #702 (comment), using the divide-and-conquer approach in reduce on static arrays may be useful for leveraging instruction-level parallelism (ILP). I cooked up two (somewhat contrived?) examples and it turned out that using divide-and-conquer approach can be 3x to 4x faster (in my laptop) than sequential (foldl) approach. This is the case when "parallelizing" both compute- and memory- bound instructions.

I also made two versions of benchmarks with and without @simd. I was surprised that putting @simd didn't help improving the foldl version.

Anyway, I think it seems to be a pretty good motivation for using this approach in StaticArrays.jl, although it'd be even nicer if there are more "real-world" benchmarks like this. What do you think? Does it make sense to use this approach in StaticArrays.jl?

Code

I'm using NTuple as a model of SVector here. mapmapreduce! is the main function that I benchmarked.

module ILPBenchmarks

@inline tmapreduce(f::F, op::O, init, ::Tuple{}) where {F,O} = init
@inline tmapreduce(f::F, op::O, init, x::Tuple{Any}) where {F,O} = f(x)
@inline tmapreduce(f::F, op::O, init, (a, b)::Tuple{Any,Any}) where {F,O} = op(f(a), f(b))
@inline function tmapreduce(f::F, op::O, init, v::Tuple) where {F,O}
    left, right = _halve(v)
    return op(tmapreduce(f, op, init, left), tmapreduce(f, op, init, right))
end

@generated function _halve(v::NTuple{N,Any}) where {N}
    m = N ÷ 2
    quote
        (($([:(v[$i]) for i in 1:m]...),), ($([:(v[$i]) for i in m+1:N]...),))
    end
end

@inline foldlargs(op::F, acc) where {F} = acc
@inline foldlargs(op::F, acc, x, xs...) where {F} = foldlargs(op, op(acc, x), xs...)

@inline tmapfoldl(f::F, op::O, init, xs::Tuple) where {F,O} =
    foldlargs((acc, x) -> op(acc, f(x)), init, xs...)

function mapmapreduce!(mapreducer::R, g::G, f::F, op::O, ys, xs, init) where {R,G,F,O}
    for i in eachindex(xs, ys)
        @inbounds ys[i] = g(mapreducer(f, op, init, xs[i]))
    end
end

function mapmapreduce_simd!(mapreducer::R, g::G, f::F, op::O, ys, xs, init) where {R,G,F,O}
    @simd for i in eachindex(xs, ys)
        @inbounds ys[i] = g(mapreducer(f, op, init, xs[i]))
    end
end

using BenchmarkTools
n = 1_000
m = 32
k = n
xs = tuple.(ntuple(_ -> rand(1:k, n), m)...)::Vector{<:NTuple{m,Any}}
ys = zeros(n)

const zs = randn(k)
@inline function memory_bound_f(x)
    y = @inbounds zs[x]
    (y, y)
end

@inline function compute_bound_f(x)
    y = x * x * x * x * x * x * x * x
    (y, y)
end

_minmax((min1, max1), (min2, max2)) = (min(min1, min2), max(max1, max2))
_diff((min, max)) = max - min

const SUITE = BenchmarkGroup()

for (simd, _mapmapreduce!) in [(false, mapmapreduce!), (true, mapmapreduce_simd!)]
    s1 = SUITE["simd=$simd"] = BenchmarkGroup()
    for (label, f) in [("memory-bound", memory_bound_f), ("compute-bound", compute_bound_f)]
        s2 = s1[label] = BenchmarkGroup()
        s2["reduce"] = @benchmarkable($_mapmapreduce!(
            tmapreduce,
            _diff,
            $f,
            _minmax,
            $ys,
            $xs,
            (Inf, -Inf),
        ))
        s2["foldl"] = @benchmarkable($_mapmapreduce!(
            tmapfoldl,
            _diff,
            $f,
            _minmax,
            $ys,
            $xs,
            (Inf, -Inf),
        ))
    end
end

end  # module

Output

Here is a typical result in my laptop:

julia> run(ILPBenchmarks.SUITE)
2-element BenchmarkTools.BenchmarkGroup:
  tags: []
  "simd=true" => 2-element BenchmarkTools.BenchmarkGroup:
          tags: []
          "compute-bound" => 2-element BenchmarkTools.BenchmarkGroup:
                  tags: []
                  "foldl" => Trial(101.073 μs)
                  "reduce" => Trial(25.643 μs)
          "memory-bound" => 2-element BenchmarkTools.BenchmarkGroup:
                  tags: []
                  "foldl" => Trial(207.505 μs)
                  "reduce" => Trial(64.472 μs)
  "simd=false" => 2-element BenchmarkTools.BenchmarkGroup:
          tags: []
          "compute-bound" => 2-element BenchmarkTools.BenchmarkGroup:
                  tags: []
                  "foldl" => Trial(99.495 μs)
                  "reduce" => Trial(25.633 μs)
          "memory-bound" => 2-element BenchmarkTools.BenchmarkGroup:
                  tags: []
                  "foldl" => Trial(197.315 μs)
                  "reduce" => Trial(64.182 μs)

[c42f]

If this give 3x speedup which we can't get another way that does seem very worthwhile.

It's worth also comparing to #494 which attacks the problem of reductions and SIMD rather differently.

[c42f]

In #702 I also wondered whether using a parallel formulation of cumsum could help ILP enough to offset the extra operations. Here's a hand written one for length-16:

function cumsum_tree_16(a)
    # Tree of partial sums
    p2  = a[1]  + a[2]
    p4  = a[3]  + a[4]
    p6  = a[5]  + a[6]
    p8  = a[7]  + a[8]
    p10 = a[9]  + a[10]
    p12 = a[11] + a[12]
    p14 = a[13] + a[14]
    p16 = a[15] + a[16]
    q4  = p2 + p4
    q8  = p6 + p8
    q12 = p10 + p12
    q16 = p14 + p16
    r8  = q4 + q8
    r16 = q12 + q16
    s16 = r8 + r16
    # Combine partial sums into full cumulative sum
    s4  = q4
    s8  = r8
    s12 = s8 + q12
    s6  = s4 + p6
    s10 = s8 + p10
    s14 = s12 + p14
    s1  = a[1]
    s2  = p2
    s3  = p2 + a[3]
    s5  = s4 + a[5]
    s7  = s6 + a[7]
    s9  = s8 + a[9]
    s11 = s10 + a[11]
    s13 = s12 + a[13]
    s15 = s14 + a[15]
    b = SVector((s1, s2, s3, s4, s5, s6, s7, s8, s9, s10, s11, s12, s13, s14, s15, s16))
end

Timings:

r = Ref(SVector(tuple((1.0:16.0)...)))

julia> @btime cumsum_tree_16($(r)[])
  4.555 ns (0 allocations: 0 bytes)

julia> @btime cumsum($(r)[])
  6.216 ns (0 allocations: 0 bytes)

so perhaps there's a benefit in this approach for Float64. Checking the generated code, it seems that no SIMD instructions are used so presumably this could be a fair bit better.

It's worse for Int64 though:

julia> @btime cumsum_tree_16($(r)[]);
  7.370 ns (0 allocations: 0 bytes)

julia> @btime cumsum($(r)[]);
  6.874 ns (0 allocations: 0 bytes)

[tkf]

Very interesting! I must confess that I was a bit skeptical if the parallel prefix is useful for cumsum for static arrays as, IIUC, speed up is only logarithmic of the number of parallel processors.

[c42f]

My thought was that for a simple cumsum the dependency chain is length N-1 which is pretty bad, but the length of the dependency chain can be a lot shorter for the parallel version (~log(N)?). In the code above I basically just implemented https://en.wikipedia.org/wiki/Prefix_sum#Algorithm_2:_Work-efficient.

[tkf]

Don't it need at least N/2 processors to achieve log N steps? I guess I just don't know what's the relevant "number of processors" when it comes to ILP.

[c42f]

what's the relevant "number of processors" when it comes to ILP.

That's exactly the point, reducing data dependencies is like getting "additional processors for free".

My understanding is that pipelining lets the hardware execute more instructions per clock cycle when there's no data dependencies. If a value from the previous instruction isn't computed yet and written to a register, it may stall the next instruction which needs to read from that register. So the throughput may be cut by a factor of several times. This is mitigated by hardware tricks like out of order execution so I'm not sure how to measure accurately in isolation.

[tkf]

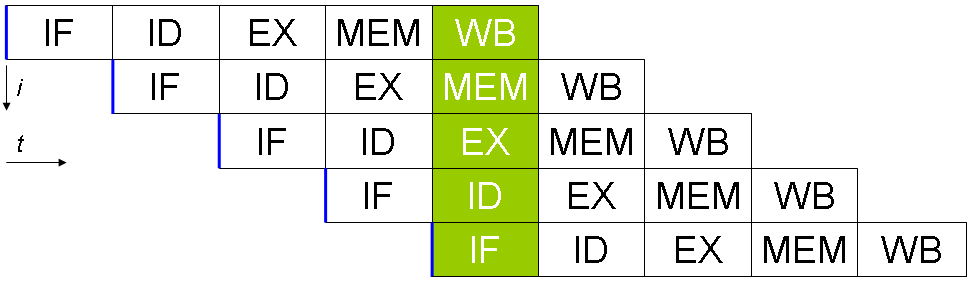
Hmm... Maybe I still don't get what pipelining does. But don't you still need to have different units (that can work in parallel)? For example, here is a picture from Wikipedia:

IIUC you get 5x more throughput here because you have 5 distinct units that are involved in the code you are executing.

[c42f]

That's true, there's different hardware units working in parallel, they're just distinct non-equivalent pieces of hardware. You could say that in this diagram we have N=5 for the purposes of ILP, but I don't think that's accurate because it depends on the type of hazard.

In the data dependency we have in cumsum, let's look at the current code:

julia> @code_native debuginfo=:none cumsum(@SVector ones(10))
	.text
	movq	%rdi, %rax
	vmovsd	(%rsi), %xmm0
	vaddsd	8(%rsi), %xmm0, %xmm1   # inst1
	vaddsd	16(%rsi), %xmm1, %xmm2  # inst2
	vaddsd	24(%rsi), %xmm2, %xmm3  # inst3
	vaddsd	32(%rsi), %xmm3, %xmm4
	vaddsd	40(%rsi), %xmm4, %xmm5
	vaddsd	48(%rsi), %xmm5, %xmm6
	vaddsd	56(%rsi), %xmm6, %xmm7
	vaddsd	64(%rsi), %xmm7, %xmm8
	vaddsd	72(%rsi), %xmm8, %xmm9
	vmovsd	%xmm0, (%rdi)
	vmovsd	%xmm1, 8(%rdi)
        ...

In the wikipedia diagram, EX for inst2 depends on WB for inst1 so in principle inst2 will be delayed for two cycles stalling the pipeline. Similarly for inst3 and inst2.

If we had a branch instruction rather than vaddsd it could be a different story — IF/ID for the next instruction would also be delayed.

But in reality we have branch prediction and out of order execution which could possibly hide pipeline stalls by overlapping them with the benchmarking harness. And I have no idea how similar the wikipedia diagram is to a real processor!

[tkf]

I think I understand that cutting data dependency helps superscalar CPU. But still, aren't there a limited number of execution units you can use at the same time? Wouldn't it create some upper bound for the effective parallelism we can have? I just wondered how it compares to the "typical large" static array sizes (Although I don't know that would be either. I noticed that N=256 is used in perf/*.jl).

Well, I guess the best way is to do some benchmarks for different vector lengths and look at the scaling.

[c42f]

But still, aren't there a limited number of execution units you can use at the same time? Wouldn't it create some upper bound for the effective parallelism we can have?

Yeah for sure there's an upper bound on the parallelism. But that doesn't imply an upper bound on the array size this is relevant to.

The straightforward method has M additions for length M+1 static arrays. The overhead of the tree should be a constant multiple of this. Let's just say the tree algorithm costs 2*M additions overall (it's a bit less). So if our improved ILP gives us 2x better throughput then we break even regardless of large M, and for a deeper pipeline we win.

[tkf]

Let's just say the tree algorithm costs 2*M additions overall (it's a bit less). So if our improved ILP gives us 2x better throughput then we break even regardless of large M, and for a deeper pipeline we win.

To connect these two sentences (in a most trivial way), don't you need the all 2*M additions to be independent?

[c42f]

Yes, it's only approximately true when there's some level of dependence between operations. In reality there's a bottleneck of dependencies in the center of the tree which might cause trouble.

My surface-level understanding is that a certain percentage of stalls can be mitigated with out of order execution and other hardware hacks, but it's hard to see how that would work if every instruction coming down the pipeline is dependent on the previous one.

[tkf]

I remember seeing https://www.llvm.org/docs/CommandGuide/llvm-mca.html and https://github.com/vchuravy/MCAnalyzer.jl so I tried using it:

julia> @inbounds function mapsum(f, xs)
           acc = f(xs[1])
           for i in 2:length(xs)
               mark_start()
               acc += f(xs[i])
           end
           mark_end()
           acc
       end
mapsum (generic function with 1 method)

julia> xs = [SVector(tuple((1.0:16.0)...))]
1-element Array{SArray{Tuple{16},Float64,1,16},1}:
 [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 11.0, 12.0, 13.0, 14.0, 15.0, 16.0]

julia> analyze(mapsum, Tuple{typeof(cumsum_tree_16), typeof(xs)})
...
Block Throughput: 34.05 Cycles       Throughput Bottleneck: Backend
...
Total Num Of Uops: 133
...

julia> analyze(mapsum, Tuple{typeof(cumsum), typeof(xs)})
...
Block Throughput: 53.02 Cycles       Throughput Bottleneck: Backend
...
Total Num Of Uops: 152
...

I have no idea how to parse the output but it says cumsum_tree_16 yields smaller number of cycles and micro-ops which means... good? Though I thought the number of ops goes up and the number of cycles go down.

Please tell me if you can decode something interesting from the full output :)

---

Full output

cumsum_tree_16

julia> analyze(mapsum, Tuple{typeof(cumsum_tree_16), typeof(xs)})
Intel(R) Architecture Code Analyzer Version -  v3.0-28-g1ba2cbb build date: 2017-10-23;16:42:45
Analyzed File -  /tmp/jl_yVOIX0/a.out
Binary Format - 64Bit
Architecture  -  SKL
Analysis Type - Throughput

Throughput Analysis Report
--------------------------
Block Throughput: 34.05 Cycles       Throughput Bottleneck: Backend
Loop Count:  22
Port Binding In Cycles Per Iteration:
--------------------------------------------------------------------------------------------------
|  Port  |   0   -  DV   |   1   |   2   -  D    |   3   -  D    |   4   |   5   |   6   |   7   |
--------------------------------------------------------------------------------------------------
| Cycles | 14.7     0.0  | 14.7  | 16.6    14.6  | 16.7    14.4  | 21.0  | 14.6  | 12.0  | 16.7  |
--------------------------------------------------------------------------------------------------

DV - Divider pipe (on port 0)
D - Data fetch pipe (on ports 2 and 3)
F - Macro Fusion with the previous instruction occurred
* - instruction micro-ops not bound to a port
^ - Micro Fusion occurred
# - ESP Tracking sync uop was issued
@ - SSE instruction followed an AVX256/AVX512 instruction, dozens of cycles penalty is expected
X - instruction not supported, was not accounted in Analysis

| Num Of   |                    Ports pressure in cycles                         |      |
|  Uops    |  0  - DV    |  1   |  2  -  D    |  3  -  D    |  4   |  5   |  6   |  7   |
-----------------------------------------------------------------------------------------
|   2^     |             |      | 0.6     0.6 | 0.4     0.4 |      |      | 1.0  |      | cmp qword ptr [r15+0x8], 0x2
|   0*F    |             |      |             |             |      |      |      |      | jb 0x273
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovapd xmmword ptr [rbp-0x40], xmm1
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovapd xmmword ptr [rbp-0x50], xmm2
|   2^     |             |      |             | 0.3         | 1.0  |      |      | 0.7  | vmovapd xmmword ptr [rbp-0x60], xmm6
|   2^     |             |      | 0.4         | 0.3         | 1.0  |      |      | 0.3  | vmovapd xmmword ptr [rbp-0x70], xmm7
|   2^     |             |      | 0.3         | 0.4         | 1.0  |      |      | 0.3  | vmovapd xmmword ptr [rbp-0x80], xmm4
|   2^     |             |      | 0.3         | 0.3         | 1.0  |      |      | 0.4  | vmovapd xmmword ptr [rbp-0x90], xmm3
|   2^     |             |      | 0.4         | 0.3         | 1.0  |      |      | 0.3  | vmovapd xmmword ptr [rbp-0xa0], xmm0
|   2^     |             |      | 0.3         | 0.4         | 1.0  |      |      | 0.3  | vmovapd xmmword ptr [rbp-0xb0], xmm5
|   2^     |             |      | 0.3         | 0.3         | 1.0  |      |      | 0.4  | vmovsd qword ptr [rbp-0x20], xmm8
|   1      |             |      |             |             |      |      | 1.0  |      | test rax, rax
|   1      |             |      |             |             |      |      | 1.0  |      | mov ecx, 0x1
|   1      |             |      |             |             |      |      | 1.0  |      | cmovnle rcx, rax
|   1      |             |      |             |             |      |      | 1.0  |      | mov eax, 0x2
|   1      |             |      |             |             |      |      | 1.0  |      | mov edx, 0xf8
|   0X     |             |      |             |             |      |      |      |      | nop word ptr [rax+rax*1], ax
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | mov rsi, qword ptr [r15]
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm0, qword ptr [rsi+rdx*1-0x78]
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x28], xmm0
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm3, qword ptr [rsi+rdx*1-0x68]
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm5, qword ptr [rsi+rdx*1-0x58]
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm4, qword ptr [rsi+rdx*1-0x48]
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm6, qword ptr [rsi+rdx*1-0x38]
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm7, qword ptr [rsi+rdx*1-0x28]
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm11, qword ptr [rsi+rdx*1-0x18]
|   2      | 1.0         |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vaddsd xmm12, xmm0, qword ptr [rsi+rdx*1-0x70]
|   2      | 0.7         | 0.3  | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vaddsd xmm9, xmm3, qword ptr [rsi+rdx*1-0x60]
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm8, qword ptr [rsi+rdx*1-0x8]
|   2      | 0.3         | 0.7  | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vaddsd xmm14, xmm5, qword ptr [rsi+rdx*1-0x50]
|   2      | 0.7         | 0.3  | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vaddsd xmm13, xmm4, qword ptr [rsi+rdx*1-0x40]
|   1      |             |      |             |             |      | 1.0  |      |      | vunpcklpd xmm3, xmm3, xmm9
|   1      |             |      |             |             |      | 1.0  |      |      | vmovddup xmm0, xmm12
|   1      | 0.3         | 0.7  |             |             |      |      |      |      | vaddpd xmm15, xmm0, xmm3
|   2      | 0.7         | 0.3  | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vaddsd xmm3, xmm6, qword ptr [rsi+rdx*1-0x30]
|   1      | 0.3         | 0.7  |             |             |      |      |      |      | vaddsd xmm9, xmm14, xmm13
|   1      |             |      |             |             |      | 1.0  |      |      | vunpcklpd xmm5, xmm5, xmm14
|   1      |             |      |             |             |      | 1.0  |      |      | vpermilpd xmm1, xmm15, 0x3
|   1      | 0.7         | 0.3  |             |             |      |      |      |      | vaddpd xmm13, xmm5, xmm1
|   2      | 0.3         | 0.7  | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vaddsd xmm5, xmm7, qword ptr [rsi+rdx*1-0x20]
|   1      |             |      |             |             |      | 1.0  |      |      | vunpcklpd xmm4, xmm4, xmm9
|   1      |             |      |             |             |      | 1.0  |      |      | vunpckhpd xmm2, xmm13, xmm15
|   1      | 0.7         | 0.3  |             |             |      |      |      |      | vaddpd xmm2, xmm4, xmm2
|   2      | 0.3         | 0.7  | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vaddsd xmm4, xmm11, qword ptr [rsi+rdx*1-0x10]
|   1      | 0.7         | 0.3  |             |             |      |      |      |      | vaddsd xmm5, xmm3, xmm5
|   1      |             |      |             |             |      | 1.0  |      |      | vunpcklpd xmm3, xmm6, xmm3
|   1      |             |      |             |             |      | 1.0  |      |      | vpermilpd xmm6, xmm2, 0x3
|   1      | 0.3         | 0.7  |             |             |      |      |      |      | vaddpd xmm10, xmm3, xmm6
|   2      | 0.7         | 0.3  | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vaddsd xmm6, xmm8, qword ptr [rsi+rdx*1]
|   1      | 0.3         | 0.7  |             |             |      |      |      |      | vaddsd xmm6, xmm4, xmm6
|   1      | 0.7         | 0.3  |             |             |      |      |      |      | vaddsd xmm6, xmm5, xmm6
|   1      |             |      |             |             |      | 1.0  |      |      | vunpcklpd xmm5, xmm7, xmm5
|   1      |             |      |             |             |      | 1.0  |      |      | vunpckhpd xmm7, xmm10, xmm2
|   1      | 0.3         | 0.7  |             |             |      |      |      |      | vaddpd xmm14, xmm5, xmm7
|   1      |             |      |             |             |      | 1.0  |      |      | vunpcklpd xmm4, xmm11, xmm4
|   1      |             |      |             |             |      | 1.0  |      |      | vpermilpd xmm7, xmm14, 0x3
|   1      | 0.7         | 0.3  |             |             |      |      |      |      | vaddpd xmm9, xmm4, xmm7
|   1      |             |      |             |             |      | 1.0  |      |      | vunpcklpd xmm6, xmm8, xmm6
|   1      |             |      |             |             |      | 1.0  |      |      | vunpckhpd xmm7, xmm9, xmm2
|   1      | 0.3         | 0.7  |             |             |      |      |      |      | vaddpd xmm6, xmm6, xmm7
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovapd xmm1, xmmword ptr [rbp-0x40]
|   1      | 0.7         | 0.3  |             |             |      |      |      |      | vaddpd xmm1, xmm1, xmm6
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm8, qword ptr [rbp-0x20]
|   2^     | 0.3         | 0.7  | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vaddsd xmm8, xmm8, qword ptr [rbp-0x28]
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovapd xmm5, xmmword ptr [rbp-0xb0]
|   1      | 0.7         | 0.3  |             |             |      |      |      |      | vaddsd xmm5, xmm5, xmm12
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovapd xmm0, xmmword ptr [rbp-0xa0]
|   1      | 0.3         | 0.7  |             |             |      |      |      |      | vaddpd xmm0, xmm0, xmm15
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovapd xmm3, xmmword ptr [rbp-0x90]
|   1      | 0.7         | 0.3  |             |             |      |      |      |      | vaddpd xmm3, xmm3, xmm13
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovapd xmm4, xmmword ptr [rbp-0x80]
|   1      | 0.3         | 0.7  |             |             |      |      |      |      | vaddpd xmm4, xmm4, xmm2
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovapd xmm7, xmmword ptr [rbp-0x70]
|   1      | 0.7         | 0.3  |             |             |      |      |      |      | vaddpd xmm7, xmm7, xmm10
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovapd xmm6, xmmword ptr [rbp-0x60]
|   1      | 0.3         | 0.7  |             |             |      |      |      |      | vaddpd xmm6, xmm6, xmm14
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovapd xmm2, xmmword ptr [rbp-0x50]
|   1      | 0.7         | 0.3  |             |             |      |      |      |      | vaddpd xmm2, xmm2, xmm9
|   1*     |             |      |             |             |      |      |      |      | cmp rcx, rax
|   0*F    |             |      |             |             |      |      |      |      | jz 0x6d
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovapd xmmword ptr [rbp-0x40], xmm1
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovapd xmmword ptr [rbp-0x50], xmm2
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovapd xmmword ptr [rbp-0x60], xmm6
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovapd xmmword ptr [rbp-0x70], xmm7
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovapd xmmword ptr [rbp-0x80], xmm4
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovapd xmmword ptr [rbp-0x90], xmm3
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovapd xmmword ptr [rbp-0xa0], xmm0
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovapd xmmword ptr [rbp-0xb0], xmm5
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x20], xmm8
|   1      |             |      |             |             |      |      | 1.0  |      | mov ebx, 0x6f
|   1      |             |      |             |             |      |      | 1.0  |      | addr32 nop
|   1      |             |      |             |             |      |      | 1.0  |      | sub rdx, 0xffffffffffffff80
|   2^     |             |      | 0.3     0.3 | 0.7     0.7 |      |      | 1.0  |      | cmp rax, qword ptr [r15+0x8]
|   1      |             | 1.0  |             |             |      |      |      |      | lea rax, ptr [rax+0x1]
|   1      |             |      |             |             |      |      | 1.0  |      | jb 0xfffffffffffffe79
|   1*#    |             |      |             |             |      |      |      |      | mov rcx, rsp
|   1      |             | 0.4  |             |             |      | 0.6  |      |      | lea rsi, ptr [rcx-0x10]
|   1*     |             |      |             |             |      |      |      |      | mov rsp, rsi
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | mov qword ptr [rcx-0x10], rax
|   1      |             |      |             |             |      |      | 1.0  |      | mov edx, 0x1
|   1*     |             |      |             |             |      |      |      |      | mov rdi, r15
|   4^     |             |      |             |             | 1.0  |      |      | 1.0  | call 0x5
Total Num Of Uops: 133
Analysis Notes:
There was an unsupported instruction(s), it was not accounted in Analysis.
Backend allocation was stalled due to unavailable allocation resources.

cumsum

julia> analyze(mapsum, Tuple{typeof(cumsum), typeof(xs)})
Intel(R) Architecture Code Analyzer Version -  v3.0-28-g1ba2cbb build date: 2017-10-23;16:42:45
Analyzed File -  /tmp/jl_DrW9SZ/a.out
Binary Format - 64Bit
Architecture  -  SKL
Analysis Type - Throughput

Throughput Analysis Report
--------------------------
Block Throughput: 53.02 Cycles       Throughput Bottleneck: Backend
Loop Count:  46
Port Binding In Cycles Per Iteration:
--------------------------------------------------------------------------------------------------
|  Port  |   0   -  DV   |   1   |   2   -  D    |   3   -  D    |   4   |   5   |   6   |   7   |
--------------------------------------------------------------------------------------------------
| Cycles | 15.5     0.0  | 15.5  | 23.7    21.3  | 23.7    20.7  | 29.0  |  7.0  |  7.0  | 23.7  |
--------------------------------------------------------------------------------------------------

DV - Divider pipe (on port 0)
D - Data fetch pipe (on ports 2 and 3)
F - Macro Fusion with the previous instruction occurred
* - instruction micro-ops not bound to a port
^ - Micro Fusion occurred
# - ESP Tracking sync uop was issued
@ - SSE instruction followed an AVX256/AVX512 instruction, dozens of cycles penalty is expected
X - instruction not supported, was not accounted in Analysis

| Num Of   |                    Ports pressure in cycles                         |      |
|  Uops    |  0  - DV    |  1   |  2  -  D    |  3  -  D    |  4   |  5   |  6   |  7   |
-----------------------------------------------------------------------------------------
|   2^     |             |      | 0.7     0.7 | 0.3     0.3 |      | 1.0  |      |      | cmp qword ptr [r15+0x8], 0x2
|   0*F    |             |      |             |             |      |      |      |      | jb 0x2b9
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x50], xmm8
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x58], xmm7
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x60], xmm6
|   2^     |             |      |             | 0.3         | 1.0  |      |      | 0.7  | vmovsd qword ptr [rbp-0x68], xmm5
|   2^     |             |      | 0.3         | 0.3         | 1.0  |      |      | 0.3  | vmovsd qword ptr [rbp-0x70], xmm4
|   2^     |             |      | 0.3         | 0.3         | 1.0  |      |      | 0.3  | vmovsd qword ptr [rbp-0x78], xmm3
|   2^     |             |      | 0.3         | 0.3         | 1.0  |      |      | 0.3  | vmovsd qword ptr [rbp-0x80], xmm2
|   2^     |             |      | 0.3         | 0.3         | 1.0  |      |      | 0.3  | vmovsd qword ptr [rbp-0x88], xmm1
|   2^     |             |      | 0.3         | 0.3         | 1.0  |      |      | 0.3  | vmovsd qword ptr [rbp-0x90], xmm0
|   2^     |             |      | 0.3         | 0.3         | 1.0  |      |      | 0.3  | vmovsd qword ptr [rbp-0x98], xmm15
|   1      |             |      |             |             |      |      | 1.0  |      | test rax, rax
|   1      |             |      |             |             |      | 1.0  |      |      | mov ecx, 0x1
|   1      |             |      |             |             |      |      | 1.0  |      | cmovnle rcx, rax
|   1      |             |      |             |             |      | 1.0  |      |      | mov eax, 0x2
|   1      |             |      |             |             |      |      | 1.0  |      | mov edx, 0xf8
|   0X     |             |      |             |             |      |      |      |      | nop word ptr [rax+rax*1], ax
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | mov rsi, qword ptr [r15]
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm8, qword ptr [rsi+rdx*1-0x78]
|   2      | 0.5         | 0.5  | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vaddsd xmm7, xmm8, qword ptr [rsi+rdx*1-0x70]
|   2      | 0.5         | 0.5  | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vaddsd xmm1, xmm7, qword ptr [rsi+rdx*1-0x68]
|   2      | 0.5         | 0.5  | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vaddsd xmm2, xmm1, qword ptr [rsi+rdx*1-0x60]
|   2      | 0.5         | 0.5  | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vaddsd xmm3, xmm2, qword ptr [rsi+rdx*1-0x58]
|   2      | 0.5         | 0.5  | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vaddsd xmm4, xmm3, qword ptr [rsi+rdx*1-0x50]
|   2      | 0.5         | 0.5  | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vaddsd xmm5, xmm4, qword ptr [rsi+rdx*1-0x48]
|   2      | 0.5         | 0.5  | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vaddsd xmm6, xmm5, qword ptr [rsi+rdx*1-0x40]
|   2      | 0.5         | 0.5  | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vaddsd xmm0, xmm6, qword ptr [rsi+rdx*1-0x38]
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0xa0], xmm0
|   2      | 0.5         | 0.5  | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vaddsd xmm9, xmm0, qword ptr [rsi+rdx*1-0x30]
|   2      | 0.5         | 0.5  | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vaddsd xmm10, xmm9, qword ptr [rsi+rdx*1-0x28]
|   2      | 0.5         | 0.5  | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vaddsd xmm11, xmm10, qword ptr [rsi+rdx*1-0x20]
|   2      | 0.5         | 0.5  | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vaddsd xmm12, xmm11, qword ptr [rsi+rdx*1-0x18]
|   2      | 0.5         | 0.5  | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vaddsd xmm13, xmm12, qword ptr [rsi+rdx*1-0x10]
|   2      | 0.5         | 0.5  | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vaddsd xmm14, xmm13, qword ptr [rsi+rdx*1-0x8]
|   2      | 0.5         | 0.5  | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vaddsd xmm15, xmm14, qword ptr [rsi+rdx*1]
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm0, qword ptr [rbp-0x98]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm0, xmm0, xmm15
|   1*     |             |      |             |             |      |      |      |      | vmovapd xmm15, xmm0
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm0, qword ptr [rbp-0x20]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm0, xmm0, xmm8
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x20], xmm0
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm0, qword ptr [rbp-0x28]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm0, xmm0, xmm7
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x28], xmm0
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm0, qword ptr [rbp-0x30]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm0, xmm0, xmm1
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x30], xmm0
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm0, qword ptr [rbp-0x38]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm0, xmm0, xmm2
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x38], xmm0
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm0, qword ptr [rbp-0x40]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm0, xmm0, xmm3
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x40], xmm0
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm0, qword ptr [rbp-0x48]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm0, xmm0, xmm4
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x48], xmm0
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm8, qword ptr [rbp-0x50]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm8, xmm8, xmm5
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm7, qword ptr [rbp-0x58]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm7, xmm7, xmm6
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm6, qword ptr [rbp-0x60]
|   2^     | 0.5         | 0.5  | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vaddsd xmm6, xmm6, qword ptr [rbp-0xa0]
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm5, qword ptr [rbp-0x68]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm5, xmm5, xmm9
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm4, qword ptr [rbp-0x70]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm4, xmm4, xmm10
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm3, qword ptr [rbp-0x78]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm3, xmm3, xmm11
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm2, qword ptr [rbp-0x80]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm2, xmm2, xmm12
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm1, qword ptr [rbp-0x88]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm1, xmm1, xmm13
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm0, qword ptr [rbp-0x90]
|   1      | 0.5         | 0.5  |             |             |      |      |      |      | vaddsd xmm0, xmm0, xmm14
|   1*     |             |      |             |             |      |      |      |      | cmp rcx, rax
|   0*F    |             |      |             |             |      |      |      |      | jz 0x72
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x50], xmm8
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x58], xmm7
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x60], xmm6
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x68], xmm5
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x70], xmm4
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x78], xmm3
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x80], xmm2
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x88], xmm1
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x90], xmm0
|   2^     |             |      |             |             | 1.0  |      |      | 1.0  | vmovsd qword ptr [rbp-0x98], xmm15
|   1      |             |      |             |             |      | 1.0  |      |      | mov ebx, 0x6f
|   1      |             |      |             |             |      |      | 1.0  |      | addr32 nop
|   1      |             |      |             |             |      | 1.0  |      |      | sub rdx, 0xffffffffffffff80
|   2^     |             |      | 0.7     0.7 | 0.3     0.3 |      |      | 1.0  |      | cmp rax, qword ptr [r15+0x8]
|   1      |             |      |             |             |      | 1.0  |      |      | lea rax, ptr [rax+0x1]
|   1      |             |      |             |             |      |      | 1.0  |      | jb 0xfffffffffffffe7b
|   1*#    |             |      |             |             |      |      |      |      | mov rcx, rsp
|   1      |             |      |             |             |      | 1.0  |      |      | lea rsi, ptr [rcx-0x10]
|   1*     |             |      |             |             |      |      |      |      | mov rsp, rsi
|   2^     |             |      |             | 0.3         | 1.0  |      |      | 0.7  | mov qword ptr [rcx-0x10], rax
|   1      |             |      |             |             |      |      | 1.0  |      | mov edx, 0x1
|   1*     |             |      |             |             |      |      |      |      | mov rdi, r15
|   4^     |             |      | 0.3         | 0.3         | 1.0  |      |      | 0.3  | call 0x5
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm9, qword ptr [rbp-0x48]
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm10, qword ptr [rbp-0x40]
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm11, qword ptr [rbp-0x38]
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm12, qword ptr [rbp-0x30]
|   1      |             |      | 0.7     0.7 | 0.3     0.3 |      |      |      |      | vmovsd xmm13, qword ptr [rbp-0x28]
|   1      |             |      | 0.3     0.3 | 0.7     0.7 |      |      |      |      | vmovsd xmm14, qword ptr [rbp-0x20]
Total Num Of Uops: 152
Analysis Notes:
There was an unsupported instruction(s), it was not accounted in Analysis.
Backend allocation was stalled due to unavailable allocation resources.

[c42f]

Wow, this is cool.

Though I thought the number of ops goes up and the number of cycles go down.

Well I suppose the number of assembly operations can go up while the number of micro-ops goes down (maybe this is what Micro Fusion occurred means)? Regardless, it's clear that less cycles is good :-D

The hardware available on the ports is documented in https://en.wikichip.org/wiki/intel/microarchitectures/skylake_(client)#Scheduler_Ports_.26_Execution_Units

I tried out llvm-mca as the backend using MCAnalyzer.analyzer[] = MCAnalyzer.llvm_mca rather than iaca and found that the documentation and generated output was quite a lot easier to understand. Even so I couldn't see how to take action based on the report!

Another thing which was interesting was enabling the timeline output and bottleneck analysis by hacking MCAnalyzer.llvm_mca to use

    Base.run(`$llvm_mca --bottleneck-analysis --timeline -mcpu $(llvm_march(march)) $asmfile`)

You can clearly see the register data dependency in the timelines, for example analyze(mapsum, Tuple{typeof(cumsum), typeof(xs)}) includes:

Timeline view:
                    0123456789          0123456789          0123456789          0123456789
Index     0123456789          0123456789          0123456789          0123456789          

[0,0]     DeeeeeeER .    .    .    .    .    .    .    .    .    .    .    .    .    .   .   cmpq	8(%rsi), %rcx
[0,1]     D======eER.    .    .    .    .    .    .    .    .    .    .    .    .    .   .   jae	.LBB0_7
[0,2]     DeeeeeE--R.    .    .    .    .    .    .    .    .    .    .    .    .    .   .   movq	(%rsi), %rdx
[0,3]     D=====eeeeeER  .    .    .    .    .    .    .    .    .    .    .    .    .   .   vmovsd	-120(%rdx,%rdi), %xmm15
[0,4]     .D====eeeeeeeeeER   .    .    .    .    .    .    .    .    .    .    .    .   .   vaddsd	-112(%rdx,%rdi), %xmm15, %xmm1
[0,5]     .D========eeeeeeeeeER    .    .    .    .    .    .    .    .    .    .    .   .   vaddsd	-104(%rdx,%rdi), %xmm1, %xmm2
[0,6]     .D============eeeeeeeeeER.    .    .    .    .    .    .    .    .    .    .   .   vaddsd	-96(%rdx,%rdi), %xmm2, %xmm3
[0,7]     . D===============eeeeeeeeeER .    .    .    .    .    .    .    .    .    .   .   vaddsd	-88(%rdx,%rdi), %xmm3, %xmm4
[0,8]     . D===================eeeeeeeeeER  .    .    .    .    .    .    .    .    .   .   vaddsd	-80(%rdx,%rdi), %xmm4, %xmm5
[0,9]     . D=======================eeeeeeeeeER   .    .    .    .    .    .    .    .   .   vaddsd	-72(%rdx,%rdi), %xmm5, %xmm6
[0,10]    .  D==========================eeeeeeeeeER    .    .    .    .    .    .    .   .   vaddsd	-64(%rdx,%rdi), %xmm6, %xmm7
[0,11]    .  D==============================eeeeeeeeeER.    .    .    .    .    .    .   .   vaddsd	-56(%rdx,%rdi), %xmm7, %xmm0
[0,12]    .  D=======================================eER    .    .    .    .    .    .   .   vmovsd	%xmm0, -24(%rbp)
[0,13]    .   D=================================eeeeeeeeeER .    .    .    .    .    .   .   vaddsd	-48(%rdx,%rdi), %xmm0, %xmm8
[0,14]    .   D=====================================eeeeeeeeeER  .    .    .    .    .   .   vaddsd	-40(%rdx,%rdi), %xmm8, %xmm9
[0,15]    .   D=========================================eeeeeeeeeER   .    .    .    .   .   vaddsd	-32(%rdx,%rdi), %xmm9, %xmm10
[0,16]    .    D============================================eeeeeeeeeER    .    .    .   .   vaddsd	-24(%rdx,%rdi), %xmm10, %xmm11
[0,17]    .    D================================================eeeeeeeeeER.    .    .   .   vaddsd	-16(%rdx,%rdi), %xmm11, %xmm12
[0,18]    .    D====================================================eeeeeeeeeER .    .   .   vaddsd	-8(%rdx,%rdi), %xmm12, %xmm13
[0,19]    .    .D=======================================================eeeeeeeeeER  .   .   vaddsd	(%rdx,%rdi), %xmm13, %xmm14
[0,20]    .    .DeeeeeE-----------------------------------------------------------R  .   .   vmovsd	-16(%rbp), %xmm0
[0,21]    .    .D================================================================eeeeER  .   vaddsd	%xmm14, %xmm0, %xmm0
[0,22]    .    .D====================================================================eER .   vmovsd	%xmm0, -16(%rbp)

The timeline view for llvm-mca is described at
https://llvm.org/docs/CommandGuide/llvm-mca.html#timeline-view

It's very interesting to see this stuff.

[c42f]

It seems the timeline output from iaca is more precise. I think here we get to see the split of ops into micro ops, so can see why one vaddsd apparently gets to start before the previous one is completed (they're split into a load and an add):

it|in|Dissasembly                                       :01234567890123456789012345678901234567890123456789012345678901234567890
 0| 0|cmp rcx, qword ptr [rsi+0x8]                      :          |         |         |         |         |         |         |
 0| 0|    TYPE_LOAD (1 uops)                            :s---deeeew----R-------p       |         |         |         |         |
 0| 0|    TYPE_OP (1 uops)                              :A--------dw----R-------p      |         |         |         |         |
 0| 1|jnb 0x1a3                                         :          |         |         |         |         |         |         |
 0| 1|    TYPE_OP (0 uops)                              :w--------------R-------p      |         |         |         |         |
 0| 2|mov rdx, qword ptr [rsi]                          :          |         |         |         |         |         |         |
 0| 2|    TYPE_LOAD (1 uops)                            :s---deeeew-----R-------p      |         |         |         |         |
 0| 3|vmovsd xmm15, qword ptr [rdx+rdi*1-0x78]          :          |         |         |         |         |         |         |
 0| 3|    TYPE_LOAD (1 uops)                            :A--------deeeew----R-------p  |         |         |         |         |
 0| 4|vaddsd xmm1, xmm15, qword ptr [rdx+rdi*1-0x70]    :          |         |         |         |         |         |         |
 0| 4|    TYPE_LOAD (1 uops)                            : A-------deeeew----R-------p  |         |         |         |         |
 0| 4|    TYPE_OP (1 uops)                              : A------------deeew----R-------p        |         |         |         |
 0| 5|vaddsd xmm2, xmm1, qword ptr [rdx+rdi*1-0x68]     :          |         |         |         |         |         |         |
 0| 5|    TYPE_LOAD (1 uops)                            : A-------cdeeeew-------R-------p        |         |         |         |
 0| 5|    TYPE_OP (1 uops)                              : A----------------deeew----R-------p    |         |         |         |
 0| 6|vaddsd xmm3, xmm2, qword ptr [rdx+rdi*1-0x60]     :          |         |         |         |         |         |         |
 0| 6|    TYPE_LOAD (1 uops)                            :  A------cdeeeew-----------R-------p    |         |         |         |
 0| 6|    TYPE_OP (1 uops)                              :  A-------------------deeew----R-------p|         |         |         |
 0| 7|vaddsd xmm4, xmm3, qword ptr [rdx+rdi*1-0x58]     :          |         |         |         |         |         |         |
 0| 7|    TYPE_LOAD (1 uops)                            :  A------ccdeeeew--------------R-------p|         |         |         |
 0| 7|    TYPE_OP (1 uops)                              :  A-----------------------deeew----R-------p      |         |         |
 0| 8|vaddsd xmm5, xmm4, qword ptr [rdx+rdi*1-0x50]     :          |         |         |         |         |         |         |
 0| 8|    TYPE_LOAD (1 uops)                            :   A-----ccdeeeew------------------R-------p      |         |         |
 0| 8|    TYPE_OP (1 uops)                              :   A--------------------------deeew----R-------p  |         |         |
 0| 9|vaddsd xmm6, xmm5, qword ptr [rdx+rdi*1-0x48]     :          |         |         |         |         |         |         |
 0| 9|    TYPE_LOAD (1 uops)                            :   A-----cccdeeeew---------------------R-------p  |         |         |
 0| 9|    TYPE_OP (1 uops)                              :   A------------------------------deeew----R-------p        |         |
 0|10|vaddsd xmm7, xmm6, qword ptr [rdx+rdi*1-0x40]     :          |         |         |         |         |         |         |
 0|10|    TYPE_LOAD (1 uops)                            :    A----cccdeeeew-------------------------R-------p        |         |
 0|10|    TYPE_OP (1 uops)                              :    A---------------------------------deeew----R-------p    |         |
 0|11|vaddsd xmm0, xmm7, qword ptr [rdx+rdi*1-0x38]     :          |         |         |         |         |         |         |
 0|11|    TYPE_LOAD (1 uops)                            :    A----ccccdeeeew----------------------------R-------p    |         |
 0|11|    TYPE_OP (1 uops)                              :    A-------------------------------------deeew----R-------p|         |