- TC: O(n)
- SC: O(1)
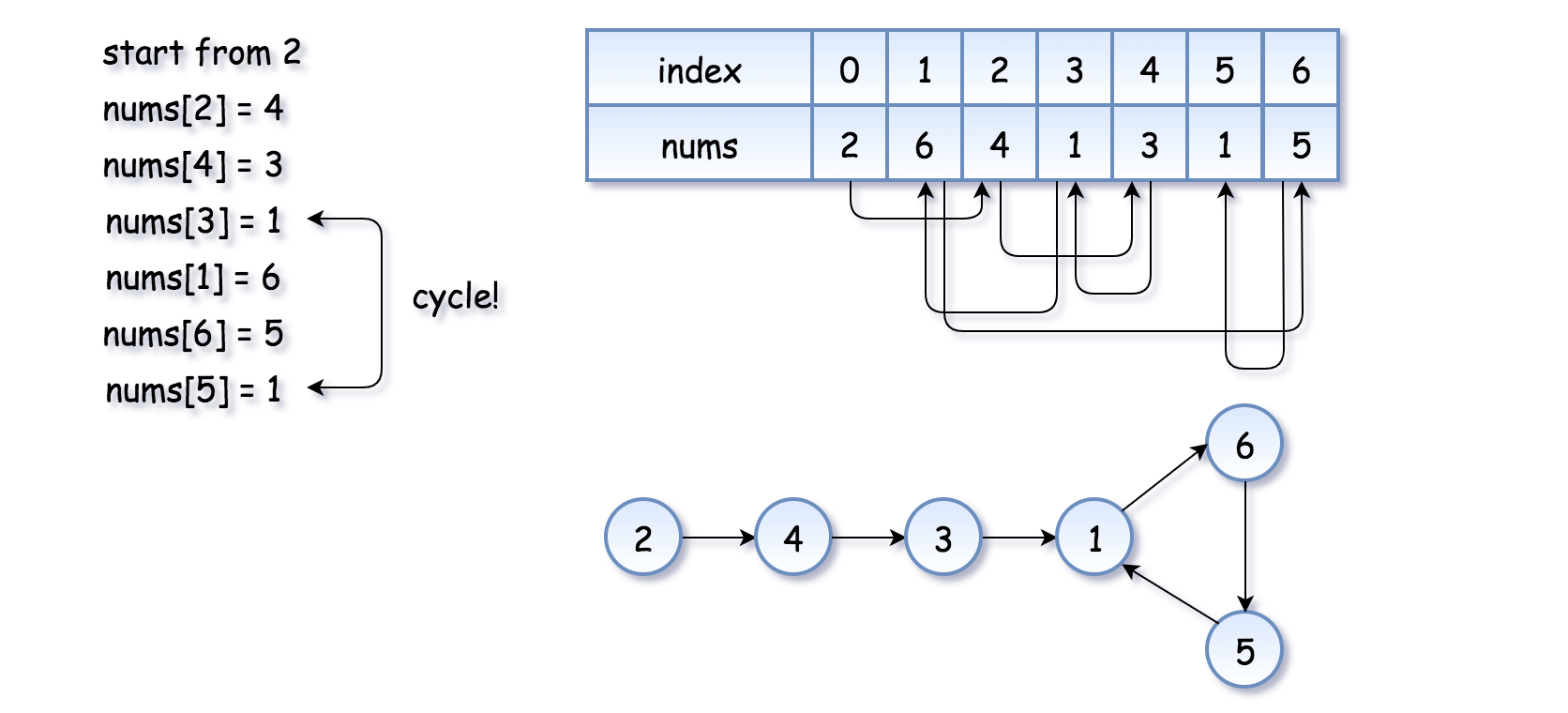
本题其中一个约束条件是数组的元素只会在 [1, n] 之间,而且有且只有一个重复元素。
打标签的思路就是:如果把每个元素当成下标来访问数组,那么重复的元素一定会导致其中一个元素被访问到两次,只要我们给访问过的元素打一个标签,之后访问的时候如果遇到这个标签就表示当前当成下标的元素就是重复的元素。
注:这是一个不错的思路,但是违反了题目不可以更改数组的要求,所以下面会提供另一种解法
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int result = -1;
for (int i = 0; i < nums.size(); i++) {
int cur = abs(nums[i]);
// 发现打过标签的元素,表示找到了重复的元素
if (nums[cur] < 0) {
result = cur;
break;
}
// 给访问过的元素打标签(置为负)
nums[cur] *= -1;
}
// 为了不被题目发现赶紧把数组偷偷改回来
for (auto& num : nums) {
num = abs(num);
}
return result;
}
};var findDuplicate = function(nums) {
let result = -1;
for (let i = 0; i < nums.length; i++) {
let cur = Math.abs(nums[i]);
if (nums[cur] < 0) {
result = cur;
break;
}
nums[cur] *= -1;
}
nums = nums.map(num=>Math.abs(num))
return result;
};- TC: O(n)
- SC: O(1)
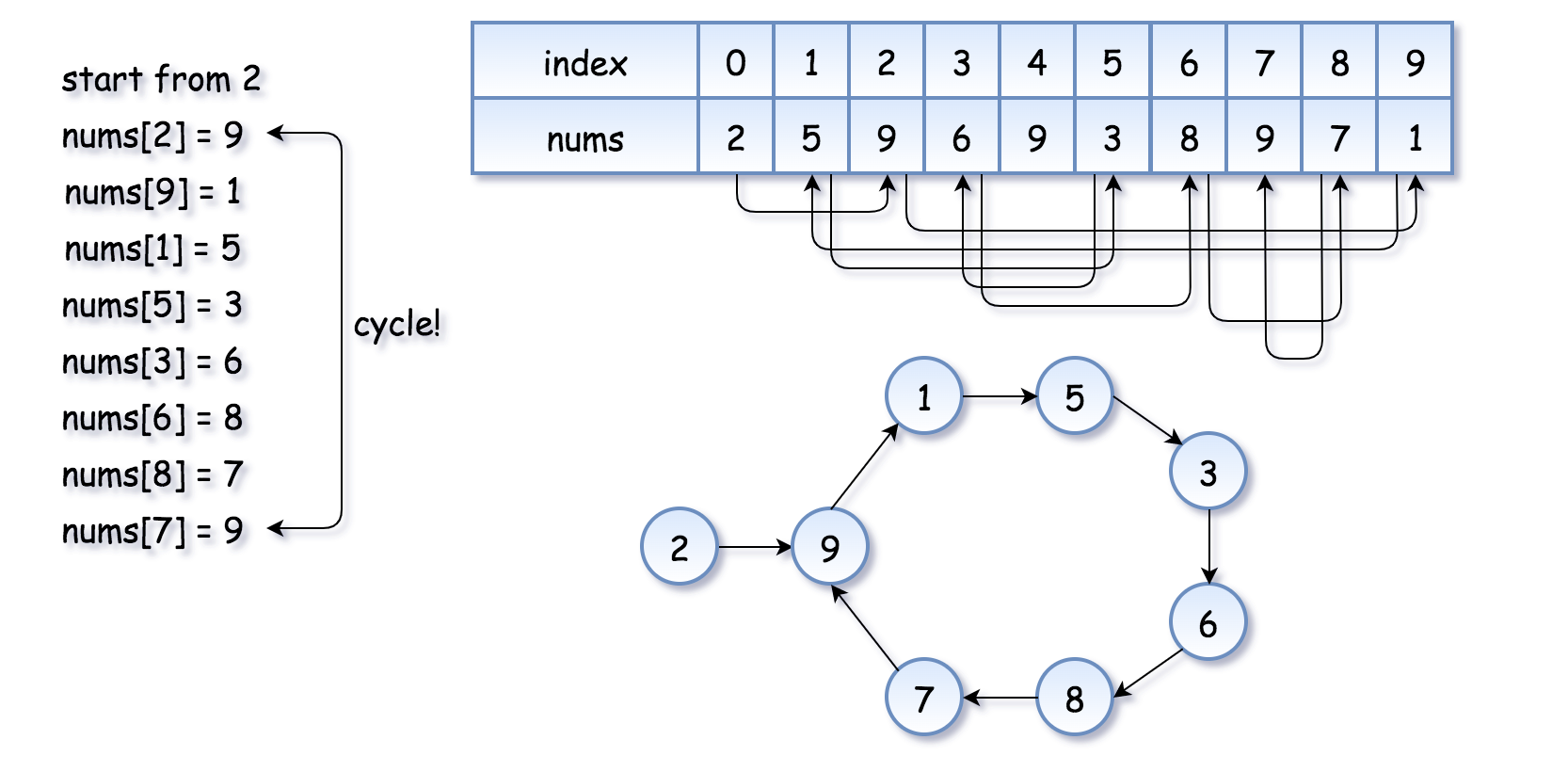
本题其中一个约束条件是数组的元素只会在 [1, n] 之间,而且有且只有一个重复元素。
也就是说,数组中的元素都可以当成数组的下标来访问其他元素。我们如果顺着这个思路,可以得到一条有环的路径(因为有重复元素),且重复的元素就是环的入口节点
参考 leetcode 官方题解的图示:
那么这道题就变成了:如何寻找有环链表的入口节点
快慢指针的思路,共分为三步:
-
用两个指针分别从链表头 pHead 出发,快指针一次走两步,慢指针一次走一步。
-
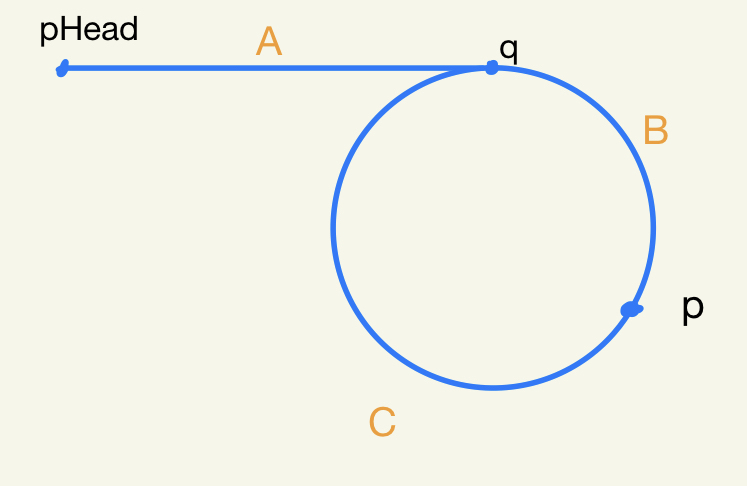
找出快慢指针相遇节点:如果有环,快慢指针必定相遇,假设相遇点为 p,环的入口节点为 q,pHead 到 q 的距离为 A,q 到 p 的距离为 B,p 到 q 的距离为 C,那么可以得出以下一幅图:
-
找出入口节点:由上图,我们可以得出一个公式
2(A+B)=A+nB+(n-1)C,其中 n 代表 B 段路径快指针走了 n 次。以上公式化简得A=(n-2)(B+C)+C。这表示 A 的路径长跟走了 n-2 圈再走一段 C 是一样长的。如果我们分别用两个指针从 pHead 与 p 开始走,那么他们相遇的第一个节点就是环的入口节点
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int fast = nums[0], slow = nums[0];
// 找到相遇的节点
do {
fast = nums[nums[fast]];
slow = nums[slow];
} while (fast != slow);
// 让快的指针从链表头开始重新走
fast = nums[0];
// 让慢的指针从相遇处开始走
while (fast != slow) {
fast = nums[fast];
slow = nums[slow];
}
// 当两个指针再次相遇的时候,就是在环的入口节点了
return fast;
}
};var findDuplicate = function(nums) {
let fast = nums[0], slow = nums[0];
// 找到相遇的节点
do {
fast = nums[nums[fast]];
slow = nums[slow];
} while (fast != slow);
// 让快的指针从链表头开始重新走
fast = nums[0];
// 让慢的指针从相遇处开始走
while (fast != slow) {
fast = nums[fast];
slow = nums[slow];
}
// 当两个指针再次相遇的时候,就是在环的入口节点了
return fast;
};