Methodology

The following methodology is used to fit profiles to binned data by calling the fit method.

Random events occur at different times following a profile P(t) with period T. Dividing the profile by the total number of events results in a periodic probability density function (pdf):

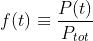
$f(t)\equiv\frac{P(t)}{P_{tot}}$

Because the pdf is periodic, it can be expanded into a Fourier series. However, low-frequency approximations of the pdf can result in periods with negative probabilities, violating one of the properties of pdfs. This can be resolved by performing the Fourier series expansion on the logarithm of the pdf, or the log-pdf. Because the pdf is periodic, the log-pdf must be as well.

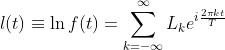
$l(t)\equiv\ln{f(t)}=\sum_{k=-\infty}^{\infty}L_ke^{i\frac{2\pi kt}{T}}$

Because Fourier series converge, they can be sufficiently approximated by a finite number of terms:

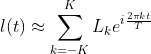
$l(t)\approx\sum_{k=-K}^{K}L_ke^{i\frac{2\pi kt}{T}}$

The proportion, p, of events between times t_a and t_b can be obtained by integrating the exponentiated log-pdf from t_a to t_b:

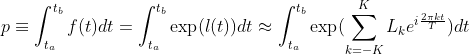
$p\equiv\int_{t_a}^{t_b}f(t)dt=\int_{t_a}^{t_b}\exp(l(t))dt\approx\int_{t_a}^{t_b}\exp(\sum_{k=-K}^{K}L_ke^{i\frac{2\pi kt}{T}})dt$

If one has the proportion of events from multiple time periods, then the Fourier coefficients L_k that minimize the error can be estimated using a nonlinear optimization algorithm. However, such algorithms can be very time consuming. Fortunately, a solution can be quickly approximated by linearizing the problem using Taylor series. To start, the integrand in the previous equation can be expanded in the following way:

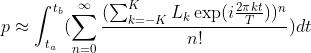
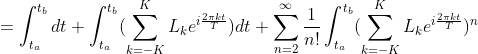
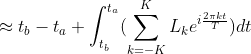
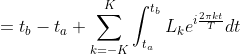
$p\approx\int_{t_a}^{t_b}(\sum_{n=0}^{\infty}\frac{(\sum_{k=-K}^{K}L_k\exp(i\frac{2\pi kt}{T}))^n}{n!})dt$ $=\int_{t_a}^{t_b}dt+\int_{t_a}^{t_b}(\sum_{k=-K}^{K}L_ke^{i\frac{2\pi kt}{T}})dt+\sum_{n=2}^{\infty}\frac{1}{n!}\int_{t_a}^{t_b}(\sum_{k=-K}^{K}L_ke^{i\frac{2\pi kt}{T}})^n$ $\approx t_b-t_a+\int_{t_b}^{t_a}(\sum_{k=-K}^{K}L_ke^{i\frac{2\pi kt}{T}})dt$ $=t_b-t_a+\sum_{k=-K}^{K}\int_{t_a}^{t_b}L_ke^{i\frac{2\pi kt}{T}}dt$ $=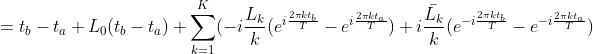t_b-t_a+L_0(t_b-t_a)+\sum_{k=1}^{K}(-i\frac{L_k}{k}(e^{i\frac{2\pi kt_b}{T}}-e^{i\frac{2\pi kt_a}{T}})+i\frac{\bar{L_k}}{k}(e^{-i\frac{2\pi kt_b}{T}}-e^{-i\frac{2\pi kt_a}{T}})$

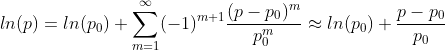
$ln(p)=ln(p_0)+\sum_{m=1}^{\infty}(-1)^{m+1}\frac{(p-p_0)^m}{p_0^m}\approx ln(p_0)+\frac{p-p_0}{p_0}$

Plugging the exponential series expansion into the logarithm series expansion (and replacing t_b-t_a with Δt) yields:

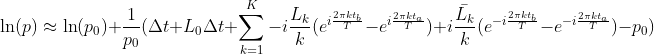
$\ln(p)\approx \ln(p_0)+\frac{1}{p_0}(\Delta t+L_0\Delta t+\sum_{k=1}^{K}-i\frac{L_k}{k}(e^{i\frac{2\pi kt_b}{T}}-e^{i\frac{2\pi kt_a}{T}})+i\frac{\bar{L_k}}{k}(e^{-i\frac{2\pi kt_b}{T}}-e^{-i\frac{2\pi kt_a}{T}})-p_0)$

Rearranging this then results in the following approximation:

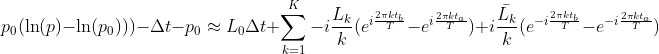
$p_0(\ln(p)-\ln(p_0)))-\Delta t-p_0\approx L_0\Delta t+\sum_{k=1}^{K}-i\frac{L_k}{k}(e^{i\frac{2\pi kt_b}{T}}-e^{i\frac{2\pi kt_a}{T}})+i\frac{\bar{L_k}}{k}(e^{-i\frac{2\pi kt_b}{T}}-e^{-i\frac{2\pi kt_a}{T}})$

Substituting p₀ with Δt further simplifies the approximation.

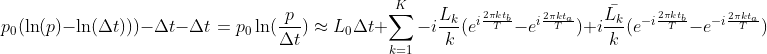
$p_0(\ln(p)-\ln(\Delta t)))-\Delta t-\Delta t=p_0\ln(\frac{p}{\Delta t})\approx L_0\Delta t+\sum_{k=1}^{K}-i\frac{L_k}{k}(e^{i\frac{2\pi kt_b}{T}}-e^{i\frac{2\pi kt_a}{T}})+i\frac{\bar{L_k}}{k}(e^{-i\frac{2\pi kt_b}{T}}-e^{-i\frac{2\pi kt_a}{T}})$

The right side of the previous equation can be expressed as a matrix product between two vectors:

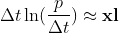
$\Delta t\ln(\frac{p}{\Delta t})\approx\textbf{xl}$

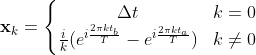
$\textbf{x}_k=\left\{\begin{matrix} \Delta t & k=0\\ \frac{i}{k}(e^{i\frac{2\pi kt_b}{T}}-e^{i\frac{2\pi kt_a}{T}}) & k\ne0 \end{matrix}\right.$

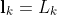
$\textbf{l}_k=L_k$

If N time periods are used, then the previous equation can be arranged into a system of linear equations.

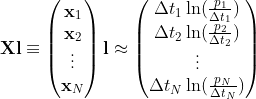
$\textbf{Xl}\equiv\begin{pmatrix} \textbf{x}_1\\ \textbf{x}_2\\ \vdots \\ \textbf{x}_N \end{pmatrix}\textbf{l}\approx\begin{pmatrix} \Delta t_1\ln(\frac{p_1}{\Delta t_1})\\ \Delta t_2\ln(\frac{p_2}{\Delta t_2})\\ \vdots \\ \Delta t_N\ln(\frac{p_N}{\Delta t_N}) \end{pmatrix}$

If N=2K+1, then the values of L_k can be solved for directly. However, if N>2K+1, then they can be found using ordinary least squares regression. Further, by setting optimize = True when running the fit method, a nonlinear optimization algorithm will better match the coefficients to the estimation data using the linear solution as an initial guess.

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

methodology.md

methodology.md

Methodology

Files

methodology.md

Latest commit

History

methodology.md

File metadata and controls

Methodology