在由 2D 网格表示的校园里有 n 位工人(worker)和 m 辆自行车(bike),n <= m。所有工人和自行车的位置都用网格上的 2D 坐标表示。
我们为每一位工人分配一辆专属自行车,使每个工人与其分配到的自行车之间的曼哈顿距离最小化。
p1 和 p2 之间的曼哈顿距离为 Manhattan(p1, p2) = |p1.x - p2.x| + |p1.y - p2.y|。
返回每个工人与分配到的自行车之间的曼哈顿距离的最小可能总和。
示例 1:
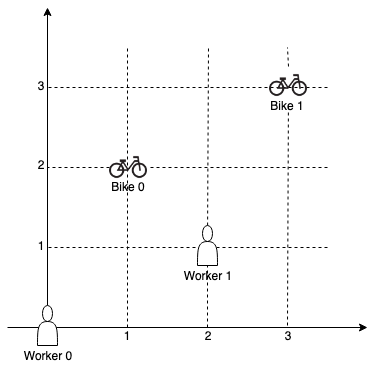
输入:workers = [[0,0],[2,1]], bikes = [[1,2],[3,3]] 输出:6 解释: 自行车 0 分配给工人 0,自行车 1 分配给工人 1 。分配得到的曼哈顿距离都是 3, 所以输出为 6 。
示例 2:
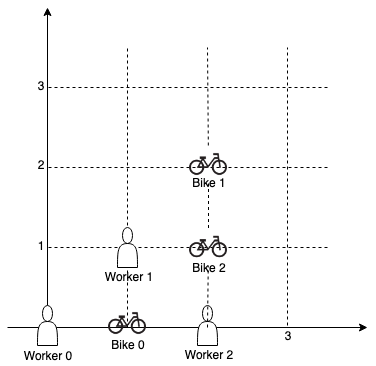
输入:workers = [[0,0],[1,1],[2,0]], bikes = [[1,0],[2,2],[2,1]] 输出:4 解释: 先将自行车 0 分配给工人 0,再将自行车 1 分配给工人 1(或工人 2),自行车 2 给工人 2(或工人 1)。如此分配使得曼哈顿距离的总和为 4。
提示:
0 <= workers[i][0], workers[i][1], bikes[i][0], bikes[i][1] < 1000- 所有工人和自行车的位置都不相同。
1 <= workers.length <= bikes.length <= 10