Skip to content

Latest commit

 

History

History
305 lines (241 loc) · 12 KB

draw-a-line.md

File metadata and controls

305 lines (241 loc) · 12 KB

用网格去拟合一条线段

推荐去我的博客阅读Draw-A-Line;

前言

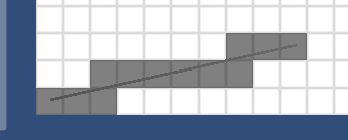
最开始是在（不记得那家公司）的笔试中，遇到了这个问题，说是给定一个线段的起点和终点，问这个线段经过了多少个网格？

示例

如上图，这个线段经过了12个格子。

当时考场上自己想了个插值法，就是每隔固定的间距$\Delta$做一次判断，将该点所在的方格添加到线段经过的方格集合中。当然这个方法是一定有bug的啦，例如：

采样点太少

采样点永远无法覆盖全部

即便采样点多一些，依然会出现上图中间那种情况，同时无限制的增多采样点也会带来比较大的性能问题。

所以我们可以用类似bfs的思路去解决这个问题。不过这个其实不是今天的重点，今天的重点是拟合，也就是说我们不需要真的把线段穿过的网格都涂黑，我们是寻找一个比较优的思路去涂黑网格，来使得得到的图像与我们画的直线尽可能拟合。

插值法

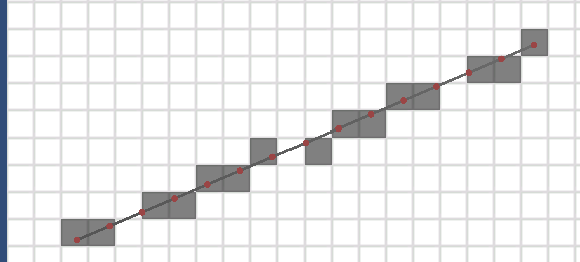
插值法的思想很好理解，我们有起点(x1, y1)和终点(x2, y2)。那么我们就可以得到线段的长度length了。随后假设我们要在线段上设置3个采样点，也就是起点，中点，终点啦，那么三个采样点的坐标都可以用着一个公式去计算：

$\begin{cases}x_i = x_1 + length \times \frac{i}{2} \ y_i = y_1 + length \times \frac{i}{2} \end{cases} \ (i = 0, 1, 2)$

推广到n个采样点，公式如下：

$\begin{cases}x_i = x_1 + length \times \frac{i}{n - 1} \ y_i = y_1 + length \times \frac{i}{n - 1} \end{cases} \ (i = 0, 1, 2 ... n - 1)$

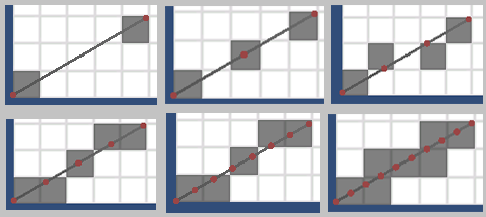
接下来就是插值法最重要的一个抉择了，到底选多少个采样点呢？ 这里我们可以这样子思考，假设(x1 = 0, y1 = 0), (x2 = 5, y2 = 3)。那么选择采样点数目2，3，4，5，8，10的效果如下图：

插值法示例

我们发现，在点数等于5的时候，我们得到了一个比较好的结果，即所有的格子都连起来了（上下左右或者对角线相邻）。小于5个点，得到的图像是中间有断点的，大于5个点，也没有明显更优（例如8个点时和5个点相同，10个点时倒是将线段经过的网格都显示出来了，但是计算量翻倍了呀）

最后其实得到的小结论就是用$Max(|x2 - x1|, |y2 - y1|)$作为采样点的个数最优，可以保证得到的结果是一个连续的图形，并且有着最少的计算次数。

证明的话，（说实话感觉画个图自己就明白了其实）

$$ \begin{align} 设格子边长为单位长度1, \\ 线段上现在有某点 (x, y), \\ 容易算出来该点所在格子坐标为(\left\lfloor x \right\rfloor, \left\lfloor y \right\rfloor); \\ ! \\ 设|x_2 - x_1| \ge |y_2 - y_1|, \\ 此时线段斜率为[-1, 1], \\ 那么设 x + 1 后，带入线段得点(x + 1, y + \Delta y); \\ ! \\ 由斜率，易知 \Delta y \in [-1, 1], \\ 由已知格子长1，和\Delta y的范围, 可得: \\ 点(x + 1, y + \Delta y) 存在于线段 (x + 1, y - 1) \sim (x + 1, y + 1)上; \\ ! \\ 而整个线段(x + 1, y - 1) \sim (x + 1, y + 1)所在的格子均与格子(\left\lfloor x \right\rfloor, \left\lfloor y \right\rfloor)相邻; \\ ! \\ 同理证明|x_2 - x_1| < |y_2 - y_1|时,\\ 线段斜率为(-\infty, -1) \cup (1, \infty), \\ ! \\ 所以y + 1后，带入线段得点(x + \Delta x, y + 1), \\ 且\Delta x \in (-1, 1), \\ 故而点(x + \Delta x, y + 1)存在于线段(x - 1, y + 1) \sim (x + 1, y + 1)上; \\ ! \\ 而整个线段(x - 1, y + 1) \sim (x + 1, y + 1)所在的格子均与格子(\left\lfloor x \right\rfloor, \left\lfloor y \right\rfloor)相邻; \\ ! \\ 同理，当x-1，y-1的情况与上述情况类似, \\ 所以可以证明用Max(|x2 - x1|, |y2 - y1|)作为采样点的个数，可以保证得到的是一个连续的图形。 \end{align} $$

代码的话也比较简单：

/*
_start      -> 线段起点 
_end        -> 线段终点
_pointCount -> 采样点数目
*/
for (int i = 0; i < _pointCount; i++)
{
    Vector2 pos = new Vector2();
    pos.x = start.x + (_end.x - start.x) * i / (_pointCount - 1);
    pos.y = start.y + (_end.y - start.y) * i / (_pointCount - 1);
    
    // 用于在界面上显示，提前初始化了若干个gameObject，
    // 用到的时候就直接设置其位置，并显示出来
    var point = _pointList[i];
    point.transform.position = pos;
    point.SetActive(true);
}

扫描法（bfs）

扫描法，这个名字是我自己瞎起的，因为感觉像是从起点一点点扫到终点，核心思想是bfs。

首先将起点所在的格子添加到队列中（假设是格子(x,y)），再假设线段终点在起点左上方时，则我们只需要去看一下格子(x + 1, y), (x + 1, y + 1), (x, y + 1)是不是被该线段穿过，如果穿过了，则将其添加到队列中。这样不断地从队列中拿出格子来，对其右上三个格子做判断，并将符合条件的加入队列，直到走到了终点为止。这样我们就可以把线段穿过的所有格子都求到。

当然，起点和终点的位置关系不同时，要检查的格子是不同的，这里其实一共只有八种方向：

  x,  y
( 1,  1) -> 左上
( 1,  0) -> 左侧
( 1, -1) -> 左下
( 0, -1) -> 下侧
(-1, -1) -> 右下
(-1,  0) -> 右侧
(-1,  1) -> 右上
( 0,  1) -> 上侧

对于方向(dirX, dirY)，对于枚举出的格子(x, y)需要去检查(x + dirX, y), (x + dirX, y + dirY), (x, y + dirY)三个格子。

接下来就是处理，如何判断线段是否经过一个格子了，这里我采用的方法是，暴力（大雾）。即计算出直线一般表达式，带入格子四个顶点，如果值全大于等于0或者全小于等于0，说明不经过。如果有大于零有小于零，说明经过。

代码稍微长一点：

/*
_curEnd   -> 线段终点
_curStart -> 线段起点
*/

// 求方向向量，如果大小小于1明显是起点终点都在一个格子内，不用管的
// 注：“方向向量”应该是单位向量，但是我们这里只需要其值的正负，所以省去Normalized过程
Vector2 dirVec = _curEnd - _curStart;
if (dirVec.sqrMagnitude < 1) return;

// 根据方向向量，计算出我们的八个方向的向量
Vector2Int dir = new Vector2Int();
dir.x = dirVec.x > 0 ? 1 : dirVec.x < 0 ? -1 : 0;
dir.y = dirVec.y > 0 ? 1 : dirVec.y < 0 ? -1 : 0;

// Debug.Log("dir: " + dir.x + " " + dir.y);

Queue<(int, int)> gridQ = new Queue<(int, int)>();

// 为起点染色
int startX = Mathf.FloorToInt(_curStart.x);
int startY = Mathf.FloorToInt(_curStart.y);
(int startGridX, int startGridY) = WorldPointToGrid(startX, startY); // 将世界坐标转为格子gameObject数组下标
ColorAGrid(startGridX, startGridY);
gridQ.Enqueue((startX, startY));

(int, int) endGrid = (Mathf.FloorToInt(_curEnd.x), Mathf.FloorToInt(_curEnd.y)); // 终点格子坐标

int layer = 0;
while (true)
{
    layer++;
    if (layer > 200) break; // 总感觉写个while(true)会有死循环卡死程序的风险所以加了个魔法数

    (int x, int y) = gridQ.Dequeue();

    // 当扫描到终点后就可以退出循环了
    if (x == endGrid.Item1 && y == endGrid.Item2)
    {
        (int gridX, int gridY) = WorldPointToGrid(x, y);
        ColorAGrid(gridX, gridY);
        break;
    }

    // 预处理出当前要被检查的格子坐标
    int[,] worldPoints = new int[,]
    {
        {x + dir.x, y},
        {x + dir.x, y + dir.y},
        {x, y + dir.y}
    };

    for (int i = 0; i < 3; i++)
    {
        int worldPointX = worldPoints[i, 0], worldPointY = worldPoints[i, 1];
        if (IsLineThroughGrid(worldPointX, worldPointY)) // 判断线段是否经过该格子
        {
            (int gridX, int gridY) = WorldPointToGrid(worldPointX, worldPointY);

            // 超出地图范围了，不用处理，
            if (gridX < 0 || gridX >= Row || gridY < 0 || gridY >= Column)
                continue;

            // 已被染色的，不再处理
            if (_grids[gridX, gridY].color != Color.gray)
            {
                ColorAGrid(gridX, gridY);
                gridQ.Enqueue((worldPointX, worldPointY));
            }
        }
    }
}

/*
careVertex -> 是否关心顶点，为true则线段经过格子顶点也算穿过格子
*/
private bool IsLineThroughGrid(int nextGridX, int nextGridY, bool careVertex = false)
{
    // Ax + by + c = 0; 直线的一般表达式
    // A = y2 - y1, B = x1 - x2, C = x2y1 - x1y2
    float A = _curEnd.y - _curStart.y;
    float B = _curStart.x - _curEnd.x;
    float C = _curEnd.x * _curStart.y - _curStart.x * _curEnd.y;

    // 格子的四个顶点
    int[,] vertexes = new int[,]
    {
        {nextGridX, nextGridY},
        {nextGridX + 1, nextGridY},
        {nextGridX, nextGridY + 1},
        {nextGridX + 1, nextGridY + 1}
    };

    // 将四个顶点代入方程
    float[] values = new float[4];
    for (int i = 0; i < 4; i++)
    {
        values[i] = A * vertexes[i, 0] + B * vertexes[i, 1] + C;
    }

    bool through;
    if (careVertex)
    {
        through = !((values[0] > 0 && values[1] > 0 && values[2] > 0 && values[3] > 0)
                    || (values[0] < 0 && values[1] < 0 && values[2] < 0 && values[3] < 0));
    }
    else
    {
        through = !((values[0] >= 0 && values[1] >= 0 && values[2] >= 0 && values[3] >= 0)
                    || (values[0] <= 0 && values[1] <= 0 && values[2] <= 0 && values[3] <= 0));
    }

    return through;
}

Extremely Fast Line Algorithm（EFLA）

参考的Po-Han Lin的算法： EFLA

我只实现了基础的三种（Division，Multiplication，Addition）。

其思路与插值法类似，先计算出线段上坐标$\Delta x，\Delta y$的关系$f(\Delta x)$，然后还是假设终点在起点的左边靠上一点$(\Delta x > \Delta y)$，这样子我们每次对x+1，就可以求出来对应的y的值，然后绘制出该点所在的格子就好了。那么问题来了，这个的效率岂不是和插值法相同的？其实确实类似，但是Po-Han Lin的算法的计算量会更小一点，具体介绍一下Division方法，另外两个是类似的思路。

  1. 首先根据线段起终点和方向向量，确定较长的边是$\Delta x$ 还是 $\Delta y$ (longLen)以及增长方向(incrementVal)。

  2. 计算出y相对x的增长率(divDiff) = longLen / shortLen。

  3. i从0到longLen枚举，每次增加incrementVal，如果longLen是$\Delta y$，则$x_i = startX + (int)(i / divDiff), y_i = startY + i$。

Po-Han Lin的代码在这里:LineA

其实他的代码处理的是线段两个端点都是整数的情况，而我的需求是线段两个端点都是实数的情况，所以做了一些微调：

bool yLonger = false;
int incrementVal;

// 判断delta X和delta Y 的大小
float shortLen = _curEnd.y - _curStart.y;
float longLen = _curEnd.x - _curStart.x;
if (Mathf.Abs(shortLen) > Mathf.Abs(longLen))
{
    var swap = shortLen;
    shortLen = longLen;
    longLen = swap;
    yLonger = true;
}

int border;
if (longLen < 0)
{
    incrementVal = -1;
    border = Mathf.FloorToInt(longLen);
}
else
{
    incrementVal = 1;
    border = Mathf.CeilToInt(longLen);
}

float divDiff;
if (shortLen == 0) divDiff = longLen;
else divDiff = longLen / shortLen;
if (yLonger)
{
    for (int i = 0; i != border; i += incrementVal)
    {
        float keyPointX = _curStart.x + (int)((float)i / divDiff);
        float keyPointY = _curStart.y + i;
        ColorAGrid(WorldPointToGrid(keyPointX, keyPointY));
    }
}
else
{
    for (int i = 0; i != border; i += incrementVal)
    {
        float keyPointX = _curStart.x + i;
        float keyPointY = _curStart.y + (int)((float)i / divDiff);
        ColorAGrid(WorldPointToGrid(keyPointX, keyPointY));
    }
}